První série třicátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

Teoretická úloha30-1-1 Oprava databáze (Zadání)

Cílem bylo spojit všechny záznamy, které spolu mají nějaké „propojení“. Emailové adresy a jména si můžeme představit jako vrcholy neorientovaného grafu a záznamy v databázi jako jeho hrany, které emaily se jménem spojují (pokud si s grafy nerozumíte, můžete se mrknout do grafové kuchařky). Jedné osobě pak libovolná dvojice vrcholů patří, pokud mezi nimi existuje libovolně dlouhá cesta – když se nachází v jedné komponentě souvislosti. Projít všechny komponenty souvislosti už jde jednoduše prohledáváním grafu do hloubky, jen je potřeba dát pozor na to, že není souvislý. Stačí si ale pro každý vrchol pamatovat, jestli už jsme jej navštívili (třeba v nějakém poli boolů). Pak všechny projdeme, a pokud jsme v něm ještě nebyli, spustíme prohledávání do hloubky. Nakonec vypíšeme počet nalezených prvků.

Samotné prohledání grafu nám zabere O(N + M), kde N je počet vrcholů a M počet hran – procházíme všechny vrcholy a pokaždé spustíme prohledávání do hloubky. Všechny prohledané vrcholy ale označíme jako „už prohledané“, takže se nikdy nespustí dvakrát prohledání stejné komponenty a každá hrana se navštíví jen jednou.

Teď zbývá vymyslet, jak vyrobit graf z databáze. Je potřeba nějakým způsobem mapovat jména a emailové adresy na vrcholy v grafu. Nejjednodušší asi bude každému textovému řetězci přidělit index v poli, do kterého si vrcholy budeme ukládat. To půjde udělat pomocí nějaké vyhledávací datové struktury – projdeme všechny záznamy, najdeme vrchol jména a vrchol emailové adresy, případně vyrobíme nový, přidáme ho do pole, a vyrobíme mezi nimi hranu.

Jako vyhledávací strukturu jste často používali hashovací tabulku, nebo vyhledávací strom, ale asymptoticky rychlejší je použít trii (písmenkový strom), která umí přidávat i vyhledávat prvky v lineárním čase s délkou textového řetězce. Hashovací tabulka to umí skoro stejně rychle, ale není deterministická, takže je konstantní jen v průměrném případě – mohla by tedy být výrazně pomalejší, kdybychom měli velkou smůlu. Vyhledávací strom by provedl logaritmický počet porovnání, které každé potřebuje až O(ℓ), kde ℓ je délka řetězce. Zpracování vstupu by pak zabralo čas O(L · log(n)), kde L je součet délek všech řetězců a n počet řetězců na vstupu.

Trie je strom, kde každý vrchol má O(Σ) synů (kde Σ je velikost abecedy), v každém vrcholu je uložen jeden znak řetězce a celá cesta do nějakého listu je jeho klíčem. Ve vrcholech, kde nějaký řetězec končí, je pak uložen i odkaz na vrchol našeho grafu. Pro šťouraly, kdybychom chtěli podporovat UNICODE, tak asi nechceme milión synů pro každý vrchol, ale stačí to zakódovat pomocí UTF-8 a pracovat s tím jako řetězci bytů. Případně řetězci bitů, to by fungovalo taky, kdyby bylo i 256 synů moc. Viz kuchařka o vyhledávání v textu, kapitola Adresář pomocí trie.

Případně je možné si pole setřídit, nejdříve podle jmen, pak přidělit indexy a pak to samé podle emailů. Třídění standardním algoritmům trvá O(n · log(n ·c)), kde n je počet prvků a c je složitost porovnání, která je úměrná délce textových řetězců. Nicméně třídit texty jde i lineárně vzhledem k součtu délek, například pomocí trie.

Algoritmus provede při stavbě grafu maximálně dvě operace s vyhledávací strukturou – vyhledání vrcholu a případně vložení nového, kde každá operace trvá trii lineárně s délkou textového řetězce. Což může být docela podstatné, v zadání nikdo neslíbil, že všichni mají hezkou a krátkou emailovou adresu, a často jste na to zapomínali. Pak je třeba graf projít – což trvá O(N + M). Dohromady to tedy trvá lineárně dlouho s velikostí vstupu v bajtech, protože počet hran i vrcholů je určitě menší než počet bajtů na vstupu.

Někteří jste také úlohu řešili pomocí datové struktury DFU (Disjoint-Find-Union), která nám umožní si pamatovat, co je s čím v jedné komponentě, a rychle tyto komponenty spojovat, když se nám vyskytne nový záznam, který „spojí“ dva lidi dohromady. Pro tuto úlohu to sice bylo maličko asymptoticky nevýhodné, ale rozhodně by se to hodilo na online verzi úlohy – kdybychom chtěli postupně zadávat záznamy a už v průběhu načítání dat vědět, kolik je to doopravdy osob. Více informací o této datové struktuře je v kuchařce o kostrách v grafu.

Program (C)

Pali Rohár & Standa Lukeš

Teoretická úloha30-1-2 Telefonní hlavolam (Zadání)

Představme si, že stojíme před telefonem, už jsme si vyžádali nějaké nápovědy a nyní přemýšlíme, zda můžeme s jistotou zmáčknout nějaké tlačítko a případně které. Určitě nemá smysl uvažovat ta tlačítka, o kterých z nějaké nápovědy víme, že je máme zmáčknout až po nějakém jiném. Zaměřme se tedy na ta ostatní a říkejme jim třeba předvoj.

Klíčem k optimálnímu řešení je si uvědomit, že tlačítko můžeme zmáčknout, jen pokud je v předvoji jediné. Proč tomu tak je? Představme si, že máme v předvoji nějaká dvě tlačítka X a Y. Správné pořadí je, dejme tomu, XAB… YPQ… Všimněte si, že když Y z tohoto pořadí „vytrhneme“ a dáme na začátek, tak nám to žádnou nápovědu „neporuší“. A tedy v současnosti ještě nemůžeme vědět, které z těchto pořadí je správné, takže nemůžeme s jistotou zmáčknout X ani Y. Naopak pokud už je v předvoji jediné tlačítko, tak jej jistě zmáčknout můžeme. Před ostatními tlačítky totiž musíme zmáčknout nějaké jiné, a jistě tedy nejsou první.

Jakmile zmáčkneme nějaké tlačítko, můžeme všechny nápovědy, které se ho týkají, zapomenout (už nám k ničemu nejsou) a celý postup opakovat se zbylými tlačítky (s využitím nápověd, které nám po „zapomenutí“ zbyly). Takto budeme postupně mačkat tlačítka v jediném správném pořadí, dokud nezmáčkneme všechna. Už víme, že na to spotřebujeme co nejméně nápověd, protože na nápovědu se ptáme jen tehdy, když je výsledné pořadí nejasné.

Z toho plyne jednoduchý algoritmus: Po každé nápovědě projdeme všechna ještě nezmáčknutá tlačítka a pro každé si spočítáme, kolik tlačítek máme podle nápověd zmáčknout před ním. Pokud nemáme před daným tlačítkem zmáčknout žádné jiné, přidáme ho do předvoje. Pokud je po zkontrolování všech tlačítek v předvoji jen jediné, zmáčkneme ho, zapomeneme o něm všechny nápovědy a postup opakujeme. Tento postup funguje, bohužel se nám ale může stát, že pro každou novou nápovědu musíme při počítání tlačítek projít skoro všechny předchozí, takže časová složitost takového řešení bude O(M2).

Neděláme však něco zbytečně? Všimneme si, že znovu a znovu u každého tlačítka přepočítáváme, kolik tlačítek musíme zmáčknout před ním. Tato čísla se ale příliš nemění: pro nějaké tlačítko B se jeho čítač změní, když dostaneme nějakou nápovědu (A, B) (to se pak čítač zvýší o jedna), nebo když naopak po zmáčknutí nějakého tlačítka A nápovědu (A, B) zapomeneme (čítač o jedna snížíme).

Budeme si tedy u každého tlačítka toto číslo pamatovat a při získání/zapomenutí nápovědy ho jednoduše přepočítáme. K tomu si pro každé tlačítko A musíme pamatovat všechny jeho nápovědy (A, B) (tj. jen všechny nápovědy „A zmáčkneme dříve než B“), abychom po jeho zmáčknutí věděli, jaké čítače máme snížit o jedničku. Kromě toho si taky budeme pamatovat aktuální předvoj, abychom uměli rychle kontrolovat, kdy už je v něm jen jedno číslo, a jaké.

Algoritmus je pak přímočarý:

Dokud máme nějaké nezmáčknuté tlačítko:

Zbývá si rozmyslet, jak toto všechno udržovat. K počítání předcházejících tlačítek nám stačí obyčejné pole čísel, pro seznam nápověd, které po zmáčknutí tlačítka projdeme, můžeme použít pole polí (nebo spojových seznamů). Pro předvoj můžeme použít například hešovací tabulku; pokud by vám vadilo, že tak získáme konstantní vkládání a mazání pouze v průměrném případě, zkuste si rozmyslet, jak k tomuto účelu upravit obyčejný spojový seznam.

Spotřebujeme nejvýše M nápověd, pro každou nápovědu provedeme jen konstantně mnoho práce. Druhý krok sice může trvat dlouho, ale dohromady každé tlačítko zmáčkneme právě jednou a každou nápovědu také zapomeneme právě jednou. Celková časová složitost je tedy O(N + M) = O(M), stejně jako paměťová.

Na závěr poznamenáme, že úloha se dala poměrně přímočaře převést na hledání topologického uspořádání v postupně budovaném grafu (nevíte-li, co je to graf nebo topologické uspořádání, zkuste se podívat do naší grafové kuchařky). Myšlenka algoritmu je stejná, jen bychom místo o tlačítkách a nápovědách hovořili o vrcholech a grafech.

Program (Python 3)

Dominik Smrž & Ríša Hladík

Teoretická úloha30-1-3 Placení v čajovně (Zadání)

Mnoho z vás se pokusilo jít na problém placení co možná nejtěžšími mincemi hladově. Většinou tak, že jste si spočetli poměr váhy ku hodnotě mince a postupně jste platili od mince s největším poměrem (abyste se zbavili co možná největší váhy).

Tento postup ale nedá nejlepší kombinaci mincí, vyvrátíme to jednoduchým protipříkladem. Představte si, že třeba existují mince o hodnotách 1, 3 a 5, kde mince s hodnotou 1 váží jednu tunu, mince o hodnotě 5 váží jeden kilogram a mince o hodnotě 3 váží jeden gram (a obvyklá peněženka obyvatel této země má podobu slušně velkého nákladního auta).

Protože nechceme, aby naše peněženka vážila více, jak my samotní, tak v ní máme jenom lehčí mince o hodnotách 3 a 5 a chceme s nimi zaplatit částku 21. Hladový postup by používal minci o hodnotě 5, dokud by se vešla (tedy čtyřikrát), a pak by se pokusil přeplatit o co možná nejméně. No a ouha, přeplatili bychom tak požadovanou částku o 2 a čajovník by nám vrátil dvě těžké mince o hodnotě 1. Správné řešení je očividně zaplatit pomocí tří mincí o hodnotě 5 a dvou o hodnotě 3.

Hladový postup dokonce ani nemusí vrátit validní kombinaci mincí. Zrecyklujme příklad výše, jenom zrušme mince o hodnotě 1. Stejně jako předtím bychom přeplatili o částku 2, ale čajovník by neměl žádný způsob, jak nám částku 2 vrátit.

Když jsme si tedy primitivní hladové postupy vyvrátili, zkusme se na to podívat trošku jinak.

Do čajovny lépe a s batohem

Nejdříve si vyřešíme lehčí úlohu: jakých hodnot a hmotností umíme dosáhnout pomocí kombinace nanejvýše K mincí N různých typů? Jedna z možností, jak to spočítat, je spustit rekurzi hloubky K a na každé úrovni rekurze se rozhodnout, jakou z N+1 mincí (přidáme si jednu virtuální minci znamenající „nepoužít nic“) zvolit. To nám ale dá čas O(NK) a přitom spousta větví výpočtu povede k tomu samému – třeba protože nám vůbec nezáleží na pořadí, v jakém mince vybereme.

Vyřešme tento problém lépe. Pojďme se dívat, jaké částky umíme dosáhnout s použitím pouze jedné mince. Pak zkusme z každé této částky vyjít a podívejme se, jaké všechny částky umíme dosáhnout s použitím dvou mincí a tak dále.

Připravme si dvourozměrnou tabulku, kde řádky budou značit počet použitých mincí a sloupce budou odpovídat poskládané hodnotě. Řádků budeme potřebovat K, počet sloupců si omezme nějakou maximální částkou M. Tabulka tedy bude mít rozměr K×M. Vyplněné políčko [i,j] v tabulce bude znamenat, že umíme s použitím i mincí dosáhnout částky j.

Dobře, ale kam se nám ztratila hmotnost? Budeme ji psát přímo do políček tabulky. Třeba pro příklad výše s mincemi 1, 3 a 5 budeme mít políčko [2,2] vyplněné váhou 2 tuny (protože pomocí dvou mincí umíme poskládat hodnotu 2 jako dvě mince o hodnotě 1). Co ale s políčkem [2,6]? To umíme poskládat jako dvě mince hodnoty 3, ale také jako jednu minci hodnoty 1 a jednu minci hodnoty 5. Druhá možnost je těžší, a tak zde zapíšeme tu.

Tabulku budeme postupně vyplňovat po řádcích. Na začátku vyplníme v prvním řádku políčka odpovídající jednotlivým mincím (kdyby nějaké dvě mince měly stejnou hodnotu, zapíšeme sem pochopitelně tu těžší) a pak budeme postupně vyplňovat další řádky. Na každé vyplněné políčko z předchozího řádku zkusíme aplikovat všech N+1 mincí (včetně té naší virtuální s hodnotou a váhou nula), a pokud nám tato kombinace dá větší hmotnost, než je zapsaná na odpovídajícím políčku ve vyplňovaném řádku, tak políčko přepíšeme novou kombinací.

Výsledky na konci výpočtu najdeme na posledním řádku. Pro získání seznamu mincí, který vedl na nějakou hodnotu, nám stačí si u každé hodnoty poznamenávat, odkud z předchozího řádku jsme na ni přišli. Pro rekonstrukci pak stačí projít tyto zpětné odkazy a vypisovat přitom hodnoty mincí.

Tím jsme právě popsali postup, kterému se velmi často říká batoh a úloze problém batohu (anglicky knapsack problem).

Ilustrace: Hroch s batohem

Nyní si naši úlohu můžeme rozdělit na dvě menší: jakou nejtěžší sadu mincí můžeme použít k zaplacení nějaké částky a obdobně to samé pro čajovníka. Úlohy se mírně liší v tom, že my máme omezené počty jednotlivých mincí, kdežto čajovník má od každé mince libovolně mnoho kusů, ale na problému to prakticky nic nezmění.

Spočítejme si nejprve, jak může vracet čajovník. Ten má sice neomezený počet kusů každé mince, ale je důležité, že obě strany mají omezený maximální počet mincí, které mohou k placení použít – v zadání jsme tyto limity označily jako K a L. Čajovník může zaplatit maximálně L mincemi, ale u každé z nich se může rozhodnout, která mince to bude.

Budeme tedy potřebovat tabulku vysokou L řádků. Šířku tabulky můžeme omezit maximální částkou, kterou můžeme zaplatit. Bohužel nelze udělat žádný odhad typu „maximálně dvojnásobek částky k zaplacení“ – zkuste si třeba zaplatit částku 45, pokud máte k dispozici jenom mince o ceně 1 000 000 007 a čajovník vám může vracet ještě navíc mince hodnoty 59 (ano, obě to jsou prvočísla). Správné řešení je zaplatit 42 velkými mincemi, aby vám čajovník mohl vrátit spoustou menších mincí. Nejlepší odhad na šířku tabulky je tak LHmax, kde Hmax je hodnota nejcennější mince.

Teď už jenom tabulku potřebujeme vyplnit. Budeme to dělat postupem popsaným výše – na každé políčko minulého řádku zkusíme aplikovat všech N+1 mincí (včetně mince znamenající „nepoužívám žádnou minci“) a tím získáme políčka v dalším řádku. V posledním řádku tak získáme všechny možné hodnoty, které může čajovník poskládat, a ke každé z nich i nejtěžší kombinaci mincí. Vyplnění této tabulky nám zabere čas O(LHmaxN), protože na každém políčku tabulky můžeme potřebovat ozkoušet všechny možné mince.

Nyní to samé budeme potřebovat udělat pro nás. Na naší straně je ale problém ztížen tím, že máme omezené počty jednotlivých mincí. Mohli bychom si u každého políčka ještě ukládat odkaz na další pole velikosti N, kde bychom si mince počítali, ale to by nás zbytečně zdržovalo.

Místo toho udělejme jednoduché pozorování, že na pořadí mincí nezáleží. Budeme tedy skládat částky tak, že si u každého záznamu v tabulce budeme pamatovat jen typ nejvyšší použité mince a počet již použitých mincí tohoto typu a dovolíme si na toto políčko navázat jenom mincí stejné nebo vyšší hodnoty. Při použití stejného typu mince musíme samozřejmě ověřit, že počítadlo nepřekročí dostupný počet mincí, a toto počítadlo inkrementujeme. Při použití vyšší mince počítadlo nastavíme na jedničku. A pokud na stejné políčko umíme se stejnou váhou přijít více způsoby, budeme preferovat ten s menším typem mince (a v případě stejných typů ten s menším počtem).

Tuto tabulku zvládneme vyplnit v čase O(KHmaxN).

Finální krok

Nyní máme vyplněné tabulky toho, jaké částky (a díky zpětným odkazům i jakou kombinací mincí) umíme na naší straně i na straně čajovníka poskládat. Z obou tabulek nás budou zajímat jenom poslední řádky (ve kterých jsou kumulované všechny výsledky pro jakýkoliv počet mincí), pojďme v nich najít nejlepší řešení.

Chceme zaplatit za čaj v hodnotě H, a to tak, že můžeme i přeplatit a čajovník nám obnos vrátí. Přitom chceme skončit s co nejlehčí peněženkou.

Zkusíme tedy projít všechny možné částky v posledním řádku naší tabulky a ke každé z nich budeme hledat v posledním řádku čajovníkovy tabulky částku k vrácení (k nějakým částkám nemusí existovat, takovým způsobem tedy zaplatit nemůžeme). Naši tabulku budeme procházet od nejmenší k největší částce, čajovníkovu naopak, a oba dva řádky nám stačí projít jednou. Přitom si budeme počítat výslednou váhu naší peněženky a na konci vydáme to nejlepší řešení.

Čaj nakoupen, teď hurá na pana Nápovědu!

Jirka Setnička

Praktická opendata úloha30-1-4 Cesta v bunkru (Zadání)

Nejprve detailně prozkoumáme, jak Hilbertovo bludiště vypadá a jaké má vlastnosti.

Anatomie Hilbertova bludiště

Připomeňme si obrázek ze zadání s bludišti řádů 1, 2 a 3:

Hilbertova bludiště řádů 1, 2, 3

Bludiště řádu r se skládá ze čtyř kvadrantů (čtvrtin), což jsou různě otočená bludiště řádu r-1. Levý horní kvadrant je otočený o 90° proti směru hodinových ručiček, pravý horní o 90° po směru, oba dolní jsou v původní poloze.

Bludiště je ohraničeho okrajem z prázdných políček. Okraje jednotlivých kvadrantů se překrývají. Část z nich tvoří okraj celého bludiště; zbytek, který leží uvnitř bludiště, tvoří tunely. Všechny tunely se potkávají ve středu bludiště; podle toho, kterým směrem ze středu vedou, je můžeme pojmenovat levý, pravý, horní a dolní tunel.

V tunelech ovšem leží 3 závaly – dodatečné zdi spojující jednotlivé kvadranty (šedá políčka na obrázku). Ty dělí tunely na dvě komponenty souvislosti: v jedné je levý, pravý a horní tunel, v druhé dolní tunel.

Nyní dokážeme, že bludiště řádu r měří (2r+1 + 1) ×(2r+1 + 1) políček (této délce strany budeme říkat velikost bludiště). Důkaz povedeme indukcí podle řádu bludiště. Bludiště řádu 1 má velikost 5. Bludiště řádu r>1 se skládá z kvadrantů řádu r-1. Ty mají podle indukčního předpokladu velikost 2r+1. Jelikož se jejich okraje překrývají o jedno políčko, velikost celého bludiště činí 2(2r+1)-1 = 2·2r + 1 = 2r+1 + 1. Tím je indukční krok hotov.

Ještě si všimneme jedné užitečné vlastnosti. Pokud z bludiště odstraníme okraj, zbude vnitřek. O vnitřku platí, že jeho prázdná políčka tvoří les (graf, jehož komponenty souvislosti jsou stromy; jinými slovy graf bez cyklů) a že každý strom lesa sousedí s okrajem v právě jednom místě (tomuto místu napojení budeme říkat portál). Dokážeme to opět indukcí podle řádu: bludiště řádu 1 má uvnitř jediné prázdné políčko, což je les o jednom stromu a tento strom sousedí s okrajem.

Indukční krok opět využívá toho, že bludiště řádu r>1 se skládá z kvadrantů řádu r. Každý z nich je lesem stromů připojených k okraji kvadrantu. Některé z nich jsou tedy připojené i k okraji celého bludiště. Ty zbylé sousedí s některým z tunelů. Tunely tedy mohou spojit více stromů dohromady, ale jelikož tunely samy neobsahují cykly, vznikne propojením stromů opět strom. A jelikož tunely vedou k okraji bludiště, každý nový strom také sousedí s okrajem.

Víme tedy, že celé bludiště bez okraje tvoří les. Navíc všechny jeho stromy jsou připojeny na okraj, takže se dá dostat z libovolného políčka do libovolného. Uvnitř téhož stromu dokonce právě jednou cestou, mezi stromy je možné po okraji projít dvěma způsoby.

Konstrukce bludiště

Abychom si rozmysleli, jak se s rekurzivní strukturou bludiště zachází, pokusíme se nejprve sestavit funkci f(r,i,j), která nám řekne, zda se v bludišti řádu r na souřadnicích (i,j) vyskytuje zeď. První souřadnice bude udávat řádek shora dolů od 0 do 2r+1, druhá podobně sloupec zleva doprava.

Označíme n=2r+1 (mez souřadnic v bludišti) a q=2r (totéž v kvadrantu).

Nejprve se postaráme o okraje: pokud buď i, nebo j je buď 0, nebo n, políčko (i,j) leží na okraji, a tedy je prázdné.

Pokud je libovolná souřadnice rovna q, políčko leží v tunelu. Není-li to některý ze závalů (q,1), (q,n-1), (q+1,q), je políčko opět prázdné.

V ostatních případech se stačí zaměřit na jeden kvadrant, tedy otázku převést na bludiště řádu r-1. Jen je potřeba souřadnice správně otočit. V levém horním kvadrantu se ptáme na f(r-1,j,q-i), v pravém horním na f(r-1,n-j,i), v levém dolním na f(r-1,i-q,j) a v pravém dolním na f(r-1,i-q,j-q).

Zbývá dořešit, jak se rekurze zastaví. Rozmysleme si, co se stane pro r=0 (to má být bludiště 3×3 s jedním jediným políčkem zdi uprostřed). Na jeho okraje odpovídáme správně, zeď na pozici (1,1) leží na předpokládané poloze tunelu (q,1), takže také hned odpovíme a dále se rekurzivně nevoláme.

Jelikož rekurze má hloubku r a na jedné úrovni trávíme konstantní čas, celý výpočet funkce f trvá O(r). Celé bludiště bychom pak zkonstruovali v čase O(2r·2r·r) = O(4r·r). (Dodejme, že to jde i v čase O(4r), tedy lineárně v počtu políček. Zkuste přijít na to, jak.)

Program (Python)

Jakmile umíme bludiště sestrojit, můžeme nejkratší cestu hledat prostým průchodem do šířky. To by fungovalo v lineárním čase s velikostí bludiště a dalo by se za to získat 10 bodů. U větších bludišť nám ovšem dojde paměť (samotné bludiště bychom si sice nemuseli pamatovat a místo toho políčka konstruovat, kdykoliv se na ně dostaneme, ale beztak musíme evidovat, kde už jsme byli, abychom se nezacyklili). U ještě větších bludišť nám dojde i čas.

Cesta na okraj

Pokusíme se najít rychlejší algoritmus, který nepotřebuje procházet všechna políčka. Budeme bludiště rekurzivně rozebírat na kvadranty a sledovat, jak se cesta proplétá mezi kvadranty. Situaci usnadní, že vnitřek bludiště je les, takže kromě průchodu okrajem je cesta určená jednoznačně.

Nejdříve vyřešíme jednodušší případ: výpočet cesty ze zadaného políčka kamkoliv na okraj. Jako výsledek budeme vracet nejen vzdálenost, ale také souřadnice políčka na okraji, kam jsme se dostali.

Mějme bludiště řádu r a políčko (i,j), z něhož se chceme dostat na okraj. Opět označíme n=2r+1 a q=2r.

Pokud i nebo j je 0 nebo n, na okraji již jsme, takže hned vrátíme 0 a (i,j). Pokud i=q nebo j=q, jsme v tunelu, takže stačí dojít na okraj. Podle toho, který tunel to je, najdeme správný portál (buď (0,q), nebo (n,q)). Do portálu jdeme pravoúhle, takže stačí spočítat pravoúhlou neboli manhattanskou vzdálenost mezi políčkem (i,j) a portálem. Manhattanská vzdálenost bodů (x,y) a (x',y') je definována jako |x-x'| + |y-y'|.

V ostatních případech leží políčko uvnitř nějakého kvadrantu. Přepočítáme tedy polohu políčka na souřadnice uvnitř kvadrantu (po patřičném posunutí a otočení), zavoláme se rekurzivně na kvadrant a pak přepočítáme souřadnice cílového políčka zpět do celého bludiště (opačné otočení a posunutí). Cílové políčko přitom leží buď na okraji celého bludiště, nebo v tunelu. Odtamtud už na okraj dokážeme dojít, takže stačí sečíst vzdálenost uvnitř kvadrantu se vzdáleností tunelem.

Rekurze má hloubku nejvýše r, na každé úrovni strávíme konstantní čas. Celkem tedy O(r).

Obecná cesta

Nyní algoritmus rozšíříme, aby uměl najít cestu mezi libovolnými dvěma políčky.

Máme-li propojit políčka (i1,j1) a (i2,j2), nejprve se podíváme, v jakých leží kvadrantech. Leží-li v tomtéž kvadrantu, chtěli bychom se na tento kvadrant zavolat rekurzivně. Ovšem pozor: může se stát, že každé políčko leží v jiném stromu, takže je potřeba propojit stromy cestou ležící mimo kvadrant. Podobně kdyby políčka ležela v různých kvadrantech, museli bychom se nejprve dostat na okraj kvadrantů a pak body na okrajích propojit.

Budeme proto řešit obecnější úlohu: pro zadané dvě políčka chceme buďto najít cestu vnitřkem bludiště (to jde, pokud jsou políčka v tomtéž stromu), anebo najít cestu z každého políčka do nějakého portálu na okraji bludiště. V prvním případě je výsledkem vzdálenost, v druhém souřadnice obou portálů a vzdálenost mezi políčky a portály.

Nyní již rekurze funguje. Pokud jsou (i1,j1) a (i2,j2) v tomtéž kvadrantu, zavoláme se na tento kvadrant. Rozlišíme dva případy:

Pokud naopak (i1,j1) a (i2,j2) leží v různých kvadrantech, spustíme na každý z nich předchozí algoritmus, čímž jsme se přesunuli do portálů na okrajích kvadrantů a ty pak propojíme výše popsaným způsobem.

Libovolný problém řádu r tedy buď převedeme v konstantním čase na problém řádu r-1, nebo ho předeveme na dva problémy „bod–okraj“ řádu r-1. Celá rekurze tedy doběhne v čase O(r).

Ale pozor, ještě nejsme hotovi: z rekurze nám může místo cesty vnitřkem vypadnout dvojice portálů na okraji celého bludiště, které ještě musíme okrajem propojit. To je potřeba udělat speciálně, protože okraj není strom. Můžeme si ale všimnout, že leží-li portály na protilehlých stranách bludiště, máme dvě možnosti, jak je propojit, takže si stačí vybrat tu kratší z nich. A pokud portály leží na téže straně bludiště, případně na dvou sousedních, stačí vždy započítat jejich manhattanskou vzdálenost, protože druhá z možných cest je nutně delší.

Program (Python)

Martin „Medvěd“ Mareš

Teoretická úloha30-1-5 Zavirování sítě (Zadání)

Nejdříve se podívejme na jeden pokus o řešení, který bohužel nefunguje. Algoritmy, které hladově infikují podle stupňů, ať už s následným odsimulováním, kam se virus rozšíří, nebo bez něj, bohužel nefungují. Podívejme se na protipříklad:

Protipříklad pro hladový algoritmus

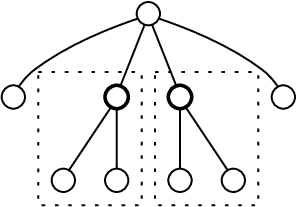
V obou tečkovaných obdélnících musí být alespoň jeden vrchol nakažen, jinak se nedají „tučné“ vrcholy nakazit. K nákaze celého grafu dokonce tyto dva vrcholy stačí. Hladové řešení by ale vybralo kořen, protože má největší stupeň, a pak by ještě muselo nakazit alespoň další dva vrcholy, tedy nejde o nejmenší řešení.

Většina odevzdaných řešení začínala jednoduchým pozorováním, totiž, že nemá smysl nakazit list. Místo něj můžeme nakazit jeho souseda a tím se ihned nakazí i on. Pojďme tuto úvahu trochu zobecnit.

Pro jednodušší přemýšlení si strom zakořeníme v libovolném vrcholu. Můžeme jít od listů a pro každý vrchol rozhodnout, zda jej na začátku nakazíme, nebo ne, jen podle již rozhodnutých vrcholů pod ním. Budeme potřebovat, abychom pro každý vrchol provedli rozhodnutí až poté, co jsou rozhodnuti všichni potomci. Někteří z vás to řešili pomocí rozdělení stromu na vrstvy, ale jednodušší je využít prohledávání do hloubky (DFS). Poté, co se vrátíme z rekurze posledního potomka, už máme všechno pod sebou rozhodnuté a můžeme se také rozhodnout.

Z rekurze budeme vracet, zda je vrchol nakažen, ať už od svých potomků, nebo ho bylo nutné nakazit na začátku. V druhém případě ho přidáme do výstupu, ale vracet budeme v obou případech stejnou hodnotu. Jak se tedy rozhodnout? Spočítáme si počet nakažených a nenakažených potomků a počet sousedů, do kterého nesmíme zapomenout započítat rodiče. Jen si musíme dát pozor na případ, kdy jsme v kořeni, který ho nemá. Podle nich rozhodneme, zda se vrchol nakazí od potomků, nebo zda se nakazí, když nakazíme i rodiče, nebo zda ho musíme nakazit na začátku.

Všimněme si, že nepotřebujeme žádnou speciální podmínku pro listy, ty přirozeně spadnou do druhé varianty. To odpovídá našemu pozorování, že se vyplatí je nechat nakazit od otce.

Tento postup bude fungovat, jelikož je po celou dobu běhu algoritmu jasně dané, kterou hodnotu musíme vrátit, a pokud můžeme ušetřit počáteční infikování, tak ho ušetříme.

Časová složitost je stejná jako pro DFS, vše stihneme provést v čase O(N), paměti budeme také potřebovat O(N).

Jirka Sejkora

Teoretická úloha30-1-6 Karetní hlavolam (Zadání)

V této úloze jste měli za úkol pracovat s operací xor. Ukázalo se, že tato neobvyklá operace nejednomu z vás zamotala hlavu a poslala vás do slepých uliček.

Pojďme se tedy odrazit od takřka univerzálního řešení na všechny úlohy – vyzkoušíme všechny možnosti. Kolik těch možností je? Každé číslo můžeme spárovat postupně se všemi ostatními, to nám dává O(N2) možností. Jelikož procesor stejně pracuje v binární soustavě, xor pro něj není problém a zvládne jej stejně rychle jako sčítání (pokud jste se s ním ještě nesetkali, tak vězte, že ve většině standardních programovacích jazyků je zapisován pomocí stříšky „^“). Takže O(N2) je i časová složitost celého algoritmu.

Výborně! Tak jsme si pořídili řešení, které nemá vůbec špatnou časovou složitost, a skoro nic nás to nestálo. Pojďme ho zkusit trošku vylepšit. Co kdybychom znali hned nejlepší číslo na spárování? Dobře, to bychom chtěli asi trošku moc, ale pojďme se podívat, jak bude vypadat pro nějaké číslo jeho ideální partner, který dá nejlepší výsledek.

Vzhledem k operaci, se kterou pracujeme, bude výhodné se na čísla koukat ve dvojkovém zápisu. Stejně tak se bude hodit, když všechna čísla budou „stejně dlouhá“, doplníme si tedy všechna čísla zleva nulami tak, aby měla stejně dlouhý dvojkový zápis.

Když tedy hledáme ideálního partnera, chceme, aby na všech místech měl opačnou cifru, tedy tam, kde má původní číslo jedničku, chceme nulu a naopak. Toto nám dá výsledek složený ze samých jedniček, což je vzhledem na naše omezení na délku největší možné číslo.

Obvykle se nám ale takto dobrého partnera najít nepodaří. V tom případě si všimněte, že nejdůležitější jsou pro nás cifry více vlevo. Když hledáme partnera pro číslo začínající jedničkou, partner musí začínat nulou (pokud nějaký takový existuje). Jakékoliv číslo, které začíná jedničkou, by totiž dalo výsledek začínající nulou, zatímco při spárování s číslem začínajícím nulou bychom dostali výsledek začínající jedničkou.

Jak tedy najdeme nejlepšího partnera pro dané číslo z těch nabízených? Jistě chceme číslo, které se liší v první cifře. Pokud je takových více, zaměříme se na ty, které se liší ve druhé cifře, a tak dále. Může se nám ale také stát, že takto v nějakém kroku vyloučíme všechna čísla. V takovém případě se nedá nic dělat a budeme muset vzít takové číslo, že výsledek bude mít na daném místě nulu. Každopádně až nám v tomto eliminačním procesu zbude jediné číslo, je to jistě náš hledaný partner.

Pomohli jsme si ale vůbec? Takto se zdá, že budeme muset pro každé číslo v nejhorším případě opakovaně procházet všechna ostatní. Klíčem bude si čísla šikovně uložit. Chceme se rychle dozvědět, jestli máme nějaké číslo, které začíná jedničkou (nebo nulou). Poté opět jestli ve zbylé skupině čísel je nějaké, které má na druhé pozici jedničku (nebo nulu), atd.

Příklad stromu

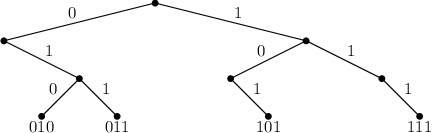
To nás nabádá si čísla ukládat v (neúplném) binárním stromu, jak vidíte na obrázku. Kořen bude reprezentovat všechna binární čísla. Vrcholy těsně pod kořenem reprezentují samostatně čísla, která začínají nulou a ty, která začínají jedničkou. Takto pokračujeme dále až listy budou reprezentovat přímo celá čísla. Může se nám stát, že nějaké skupiny budou celé chybět, v tom případě bude chybět i příslušný vrchol v daném stromu.

V takovémto stromu se už jednoduše najde nejlepší partner. Čteme původní číslo po cifrách a vždy, pokud je to možné, se vydáme dolů opačnou hranou, než je příslušná cifra. Pokud to možné není, jdeme dolů zbylou hranou (v tom případě bude ve výsledku na dané pozici nula).

Jednoduché je i tento strom postavit. Začneme se samotným kořenem a postupně přidáváme všechna čísla. Každé číslo čteme po cifrách. Pokud ještě ve stromu hrana odpovídající dané cifře neexistuje, tak ji vytvoříme a přesuneme se po ní dolů. Jestli ve stromu už je, tak ji vytvářet nemusíme, jen se po ní vydáme.

Pro každé číslo nám tedy stačí strom dvakrát projít od kořene až k listu (jednou při vytváření a jednou při hledání partnera). Všimněte si, že strom je tak vysoký, jak je dlouhé největší číslo ve dvojkovém zápise. Tedy jinými slovy jako jeho dvojkový logaritmus.

Na začátku jsme předpokládali, že čísla na vstupu jsou dostatečně malá, takže i jejich ciferný zápis je krátký, a tedy hloubka stromu je jen konstantní. Mohli bychom tuto konstantu při počítání složitosti jednoduše zanedbat. Koneckonců na začátku jsme řekli, že xor zvládneme v konstantním čase, což je pravda jen pro dostatečně malá čísla, typicky 264, nebo přesněji libovolná konstantou omezená čísla. Buďme ale v tomto poctivější a velikost největšího čísla zahrňme do počítané časové složitosti (vyjádříme tedy časovou složitost našeho algoritmu pro libovolně velká čísla na vstupu). Navíc si všimněte, že xor zvládneme rovnou počítat už při hledání partnera, takže i tak nám stačí počítat xor jednobitových čísel.

Jelikož čísel máme N, dostaneme se na celkovou časovou složitost O(N log k), kde k je největší číslo. Paměťová bude stejná, jelikož si potřebujeme pamatovat celý strom.

Poznámka na závěr. Při programování se vám může hodit operace bitový posun, která se typicky zapisuje jako „<<“ resp. „>>“. Tedy například 5 << 2 znamená vezmi pětku a (v binárním zápisu) ji posuň o dvě místa doleva (a zprava doplň nulami). Pokud vám to trošku zamotalo hlavu a zaráží vás, proč zvládneme xor v konstantním čase jen pro dostatečně malá čísla, tak trošku světla pomůže vnést náš letošní seriál!

Program (Python 3)

Dominik Smrž

Seriálová úloha30-1-7 Assembler (Zadání)

Předně nám dovolte omluvit se za počet chybek, které se nám do seriálu vloudily. Bohužel se zdá, že džungle assemblerů je občas opravdu divoká a i my jsme v ní nejednou zabloudili. Naštěstí jste se nenechali zmást například chybějící variantou MUL s číselnou konstantou a dorazilo nám spoustu pěkných řešení.

Úkol 1: Povrch kvádru

Chceme do assembleru přepsat formuli S = 2  · (ab + bc + ca). Nejsnazší je jednotlivé matematické operace přímo přepsat do instrukcí assembleru:

	MUL r0, r1, r2 @ r0 = ab
	MUL r1, r3     @ r1 = ac
	MUL r2, r3     @ r2 = bc
	ADD r0, r1     @ r0 = ab + ac
	ADD r0, r2     @ r0 = ab + ac + bc
	MOV r4, #2
	MUL r0, r4     @ r0 = 2 * (ab + ac + ca)

Existuje však i lepší řešení – násobení je obecně pro procesor docela drahá operace, a tak je lepší se jí vyhnout, pokud to umíme. Pro případ násobení dvěma by šlo použít bitový posun doleva, který jsme si neukazovali, ale stejně tak lze využít jednoduchého faktu, že 2  · a = a + a:

	MUL r0, r1, r2 @ r0 = ab
	MUL r1, r3     @ r1 = ac
	MUL r2, r3     @ r2 = bc
	ADD r0, r1     @ r0 = ab + ac
	ADD r0, r2     @ r0 = ab + ac + bc
	ADD r0, r0     @ r0 = 2 * (ab + ac + ca)

Úkol 2: Podmínky

Chceme, aby existoval společný začátek, potom nějaké rozvětvení na if/else a následně aby se tyto větve zase spojily v jednu. Pokud pouze triviálně zapíšeme tuto myšlenku do assembleru, získáme něco takového (násobení dvěma opět píšeme jako sečtení samo se sebou):

	CMP r1, #0
	BEQ if
	BNE else

if:
	ADD r0, #1
	B both

else:
	SUB r0, #1
	B both

both:
	ADD r2, r0, r0

Jenže opravdu na takovýto jednoduchý if potřebujeme až čtyři různé instrukce skoku? Snadno nahlédneme, že skok B both v bloku else je naprosto k ničemu – „skočí“ na násedující instrukci, tedy tam, kam se stejně procesor chystá pokračovat. Pokud bychom navíc řádky BEQ if a BNE else prohodili, všimneme si, že můžeme ušetřit ještě jeden skok. Ideální řešení tedy vypadalo zhruba takto:

	CMP r1, #0
	BNE else

	ADD r0, #1
	B endif
else:
	SUB r0, #1
endif:
	ADD r2, r0, r0

Úkol 3: Největší společný dělitel

Správným algoritmem pro řešení tohoto problému je samozřejmě Euklidův algoritmus. Více o něm se můžete dočíst v naší kuchařce. V tomto případě nám ani nešlo tolik o zvolenou variantu tohoto algoritmu, ale o to, popasovat se s absencí instrukce modulo, tedy instrukce, která spočítá zbytek po dělení.

Jedno řešení tohoto problému je odčítat dělitele, dokud nedojdeme k zápornému číslu, a pak ho jednou zpět přičíst. Například spočítání r0 = r0 mod r1 může vypadat takto:

modulo:
	SUBS r0, r1
	BPL modulo

	ADD r0, r1

Druhá možnost využívá celočíselného dělení. Platí, že x = a · y + b. Tomu říkáme, že „x děleno y je a, zbytek b“. ARM nám však umí spočítat a pomocí celočíselného dělení! Když známe a, můžeme ho vynásobit y a po odečtení od x získáme b, náš hledaný zbytek. V řeči assembleru:

	SDIV r2, r0, r1  @ r2 = a
	MUL r2, r1       @ r2 = a * y
	SUB r0, r2

My se rozhodneme pro odčítací verzi modula. Ač má tento postup asymptoticky horší složitost, pro mnoho procesorů je instrukce pro dělení stále příliš velký luxus, a tohle řešení je tedy univerzálnější. Celý algoritmus by mohl v pseudokódu vypadat například takto:

while b <> 0:
	tmp := b
	b := a
	b := a mod tmp
	a := tmp

V assembleru potom například takto:

	MOV r1, #84
	MOV r2, #72

while:
	MOV r0, r2
	MOV r2, r1
modulo:
	SUBS r2, r0
	BPL modulo
	ADD r2, r0

	MOV r1, r0

	CMP r2, #0
	BGT while

Honza Gocník