Druhá série třicátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 22. ledna 2018
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Sladkou odměnu si vyslouží každý, kdo vyřeší každou úlohu s lehkou variantou alespoň na polovinu bodů.

Zadání úloh

• 30-2-1: Zaneprázdněný org
• 30-2-2: Hardwarový generátor
• 30-2-3: Šíření viru podruhé
• 30-2-4: Komprimace
• 30-2-5: Autovysavač
• 30-2-6: Parlamentní metro
• 30-2-7: Paměť očima assembleru

V budově Matfyzu na Malostranském náměstí je Rotunda jednoznačně největší a nejkrásnější místností. Je to vysoká kruhová dvorana sahající až do dalšího patra, kde skleněné stěny nabízí pohled do prostor školní knihovny. Kdysi se v Rotundě nacházely prostory národní banky, ale ty časy jsou už dávno pryč. Místo toho tu jsou do kruhu seřazené počítače, nalevo unixové, vpravo windowsové, jako kdyby se co nevidět měly pustit do boje. Venku se už dávno setmělo a otevírací doba počítačové laboratoře (neboli labu, jak říká každý správný matfyzák) se chýlí ke konci. Dělal jsem tu dnes celý den službu a teď zbývá lab, beztak už prázdný, zamknout.

Beru si věci, jdu ke dveřím a chystám se zhasnout světla, když vtom uvidím zvláštní věc. U jednoho z unixových počítačů úplně nalevo se rozblikala červená ledka. Co to má znamenat? Ani jsem nevěděl, že nějaký počítač v labu by uměl takhle blikat. Chci přijít blíž, ale pak si všimnu, že se úplně stejně rozblikal jeden z počítačů napravo. A po chvilce další. A další. A zanedlouho blikají červeně všechny počítače, a k tomu všemu navíc úplně synchronně.

„To je ale blbej vtip,“ mumlám si pro sebe, ale spíš chci zakrýt fakt, že jsem se začal trochu bát. Přijdu k jednomu ze strojů a pohnu myší. Displej se rozzáří a já vidím…

* * *

„…a Turingův stroj se vždycky zastaví.“

Pane jo, já jsem zase usnul na přednášce? To by nebylo poprvé, ale nepamatuji si, že by se mi zdálo o sloužení v labu. Semestr už začal, musím ještě řešit resty z toho minulého, a do toho mi ostatní orgové KSP dají za úkol řídit vyšetřování toho, kam vlastně zmizel pan Nápověda. Jsem si jistý, že podobně perné týdny jsem měl minulý rok, ale musel bych se podívat do své databáze, jestli tomu tak opravdu bylo.

30-2-1 Zaneprázdněný org (11 bodů)

Náš vypravěč, organizátor KSPčka, si již dlouhou dobu zaznamenává, jak byl pro něj který týden hektický. Databázi těchto záznamů si můžete představit jako posloupnost celých čísel A_i, kde i představuje pořadové číslo týdne od samotného začátku měření. Hodnota každého prvku posloupnosti popisuje orgovu zaneprázdněnost během týdne.

Máte databázi k dispozici a chtěli bychom po vás, abyste uměli rychle odpovídat na dotazy „Kolikrát se vyskytlo v týdnech od x do y hodnocení H?“, neboli „Kolikrát se v podposloupnosti A_x až A_y vyskytuje číslo H?“. Dotazů může být mnoho, a proto se může hodit si na začátku předpočítat nějaká data a ta poté použít při odpovídání na dotazy. V takovém případě nás zajímají časové a paměťové složitosti jak předpočítání, tak jednoho dotazu.

Příklad vstupu: Posloupnost A_i je 1, 2, 2, 3, 2, 2, 3, 3. Předpokládáme, že indexujeme od jedničky. Na dotaz „kolikrát se od druhého do pátého týdne vyskytla zaneprázdněnost 2“ je odpověď 3, na dotaz „kolikrát se od pátého týdne do osmého týdne vyskytla zaneprázdněnost 3“ je odpověď 2.

Lehčí varianta (za 6 bodů): Řešte pro jednodušší dotazy „Vyskytuje se v týdnech od x do y hodnocení H?“.

Řešení

30-2-2 Hardwarový generátor (13 bodů)

Máme seznam M prvků a chceme z něj náhodně vybírat prvky. U každého prvku máme uvedené, s jakou pravděpodobností má být vybrán (pravděpodobnosti všech prvků se správně posčítají na 1).

Protože nevěříme tradičním generátorům čísel, používáme náš vlastní, hardwarový generátor. Ten však umí jedinou věc: rovnoměrně generovat nějaké číslo z uzavřeného intervalu [0,1].

Rovnoměrností myslíme, že všechna čísla mají stejnou šanci být vygenerována. (Kdybychom to chtěli definovat pořádně, nestačilo by říci, že mají stejnou pravděpodobnost, protože ta je pro každé z nekonečně mnoha čísel nulová. Mohli bychom třeba říci, že pro každý podinterval délky p platí, že se do něj strefíme s pravděpodobností přesně p.)

Určete, jak budete opakovaně náhodně vybírat prvky množiny se zadanými pravděpodobnostmi jen s pomocí našeho generátoru. Předpokládejte, že umíte přesně počítat s reálnými čísly, nevznikají zaokrouhlovací chyby a generování jednoho náhodného čísla probíhá v konstantním čase. Optimalizujte nejprve na čas strávený při generování jednoho prvku, následně pak na čas předvýpočtu před prvním generováním.

Známe řešení, které tráví na předvýpočtu O(M) a následná generování zvládne v konstantním čase. Vymyslíte nějaké stejně rychlé? Pokud ne, určitě pošlete i to pomalejší, také za něj dostanete body.

Příklad vstupu: Máte prvky A, B a C. A chcete generovat s pravděpodobností 1/6, B s pravděpodobností 1/3 a C s pravděpodobností 1/2.

Řešení

30-2-3 Šíření viru podruhé (10 bodů)

Máte síť N navzájem propojených počítačů. V této síti zkoumáte chování viru, jehož úkolem je nakazit co nejvíce počítačů. Virus se ale nešíří úplně přímočaře. Máme seznam dvojic počítačů a u každé dvojice (A,B) platí, že se virus může přímo přenést z počítače A do počítače B (obráceně to být nemusí – pokud ano, tak se v seznamu vyskytuje další dvojice (B,A)).

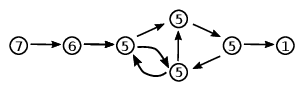
Předpokládáme, že na začátku útoku je virus jen v jednom počítači v síti, odtud se rozšíří na všechny počítače, které dokáže přímo nakazit, následně se z těchto počítačů opět přenese dál, jak může… a takhle pokračuje, dokud je šíření možné. Pro každý počítač P chceme najít počet strojů, které se nakazí, pokud bude P nakažen na začátku útoku. Můžete se podívat na obrázek s příkladem. Kroužky odpovídají počítačům, dvojice počítačů, kde první může nakazit druhý, jsou propojeny a číslo u počítače P odpovídá počtu napadených počítačů, pokud je virus na začátku v P.

Lehčí varianta (za 6 bodů): Řešte stejnou úlohu za předpokladu, že v seznamu přenosů není cyklus.

Řešení

Displej ukazuje šíření viru a já si mimoděk vzpomenu na ten divný sen na přednášce. To s těmi blikajícími počítači se nestalo, ale když to vidím, tak se nemůžu nezeptat: „Janka, určitě se ten program z těch virtuálních mašin nemůže dostat ven?“

„Nie,“ odpověděla. Ale nic dalšího neřekla, zavřela notebook a odešla. Jaký výraz měla ve tváři, to jsem kvůli těm černým brýlím nemohl odhadnout.

Zbytek dne jsem strávil podivně zmatený. Hlavou se mi honily podivné myšlenky. Vybavovaly se mi osoby, se kterými jsem se neznal, a místa, na kterých jsem určitě nikdy nebyl. Je vážně na čase se pořádně vyspat, řekl jsem si, navíc zítra máme kvůli vyšetřování nějakou zajímavou návštěvu.

* * *

Místnost S322 je základnou každého KSPáka, takže v devět hodin ráno (ano, ráno) tam jen tak na někoho nenarazíte. Když už ano, tak dotyčný vypadá, jako by právě vylezl z postele, a k dokonalému dojmu chybí jen pyžamo. Dnes jsme tu ale hostili partičku mediků, a to kvůli jednomu ze souborů v Nápovědově počítači, který podezřele připomínal sekvenci DNA. Než jsme se k souboru prokousali, museli jsme pochopit některé netradiční komprimační metody, které Nápověda používal.

30-2-4 Komprimace (10 bodů)

Vaším úkolem je rozbalit zkomprimovaná data. K jejich komprimaci došlo následujícím způsobem:

Data zapsaná jako posloupnost bitů se rozdělila na posloupnost různě dlouhých bloků. Každý blok je pak ve zkomprimovaném souboru reprezentován jedním ze dvou způsobů. První způsob je jednoduchý, data bloku jsou zapsána přímo tak, jak byla v původním souboru. Druhý způsob umožňuje zkrátit zápis opakujících se kusů DNA. Místo samotných dat je zde pouze reference (odkaz) na kus původních dat, která jsou s daným blokem shodná. Reference na pozici i tedy znamená, že nultý bit bloku je shodný s i-tým bitem původních dat, první bit bloku s (i+1)-ním bitem atd., až do vyplnění celého bloku.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete dvě mezerou oddělená čísla N a M. Číslo N značí počet bitů původního souboru a M počet bloků. Následuje M řádků, každý reprezentuje jeden blok. Každý z těchto řádků obsahuje 3 údaje oddělené mezerou. První je typ zápisu dat (D = data, nebo R = reference), druhý je velikost bloku. Třetí údaj je buď posloupnost bitů (tedy posloupnost nul a jedniček), pokud blok obsahuje přímo data, nebo odkaz na začátek úseku, jehož obsah je shodný s daty bloku (adresy bitů číslujeme od nuly). Bloky na vstupu jsou přesně v pořadí, jak jdou za sebou v původním souboru.

Formát výstupu: Na výstup vypište původní dekomprimovaný soubor, tedy posloupnost nul a jedniček, pokud je určena jednoznačně. Mohla se nicméně někde stát chyba a původní data nemusí jít ze zkomprimovaných informací určit jednoznačně, posloupnost původních bitů tedy nejde zrekonstruovat. V takovém případě vypište NEJDE.

7 5
R 1 4
D 2 11
R 2 5
R 1 2
D 1 0

0111010

4 3
R 1 3
D 2 10
R 1 0

NEJDE

10 2
D 2 01
R 8 0

0101010101

Řešení

30-2-5 Autovysavač (12 bodů)

Kuba, respektive pomocník pana Nápovědy v Kubově těle, si „vypůjčil“ nový stroj Pražských služeb: obří vysavač na odpadky. Právě ho přivezl ho na parkoviště na Malostranském náměstí, a protože si chce vytvořit volný prostor, chce s ním nasát nějaká z aut, která tu parkují. Protože je pomocník škodolibý, chtěl by nasátím zničit co nejdražší auta, konkrétně takovou skupinu aut, aby medián jejich cen byl co nejvyšší.

Jak definujeme medián pro množinu čísel? Provedeme to jen pro případ, že je v množině lichý počet prvků. Pokud seřadíme čísla v množině podle velikosti, je medián tím číslem, které se nachází uprostřed seznamu, Platí tedy, že 50 % ostatních čísel je menší nebo rovno mediánu a 50 % je vyšší nebo rovno mediánu.

Parkoviště reprezentujeme jako čtverečkovou síť o rozměrech M×N. V každém poli je uvedena hodnota zde stojícího auta. Vysavač dokáže vysát nějakou obdélníkovou oblast o rozměrech P×Q polí. Zjistěte, která oblast této velikosti má nejvyšší medián cen – máte jistotu, že P·Q je vždy liché.

Mějme například parkoviště velikosti 4 ×4 s následujícími hodnotami cen aut, přičemž dokážeme vysát oblast 3 ×3:

200 30 10 40
20  10 50 40
60  60 10 40
10  10 10 20

Ačkoliv je nejdražší auto v levém horním rohu, medián této oblasti velikosti 3×3 je jen 30. Lepší je pravá horní oblast 3×3, která má medián 40.

Lehčí varianta (za 6 bodů): Řešte za předpokladu, že N = 1.

Řešení

30-2-6 Parlamentní metro (12 bodů)

Za časů studené války vznikla v Praze tajná podzemní dráha s jediným účelem – evakuovat politiky a státníky v případě hrozící jaderné apokalypsy. Metro má mnoho stanic, které jsou propojeny tunely. Do jedné stanice může ústit libovolný počet tunelů, a ať už vlak přijede z jakéhokoliv směru, může se vydat dál jakýmkoliv tunelem.

Z bezpečnostních důvodů není metro napojeno na elektrickou síť, místo toho je každý vlak poháněn svou vlastní baterií. Aby měly vlaky co nejmenší tření, je z tunelů vypuštěn vzduch a vlaky se pohybují jen po magnetické kolejnici. Znamená to, že energii musí vlak vyvinout jen v momentě, když vyjíždí ze stanice, a to tím větší energii, čím větší rychlost chce vyvinout. Na délce úseku mezi stanicemi spotřeba vůbec nezávisí. Vlak ale musí (z bezpečnostních důvodů) zastavit v každé stanici na cestě.

Formálněji, vede-li mezi dvěma stanicemi tunel s délkou  s a vlak jím projede rychlostí v, urazí celou trasu za s/v jednotek času a bude ho to stát v jednotek energie (čas na rozjíždění a brždění zanedbáváme).

Pro danou počáteční a cílovou stanici a zadané nabití baterie rozhodněte, jak se co nejrychleji dostat ze startu do cíle, abychom si přitom vystačili pouze s energií z baterie. Kromě seznamu stanic v pořadi, v jakém je navštívíme, nás zajímají i rychlosti, kterými budeme projíždět tunely mezi nimi.

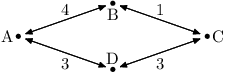
Příklad: Pro následující rozložení stanic, počáteční stanici A, koncovou stanici C a baterii s kapacitou 6 jednotek je optimálním řešením jet přes stanici B, a to následovně: Na úseku A–B pojedeme rychlostí 4, na úseku B–C rychlostí 2, dohromady tedy využijeme celou baterii. Celkový čas cesty bude 4/4 + 1/2 = 3/2 jednotek. Kdybychom místo toho jeli přes D, nestihli bychom se do cíle dostat dříve než za dvě časové jednotky.

Lehčí varianta (za 7 bodů): Všechny stanice tvoří jednu souvislou trasu – z koncových stanic vede jediný tunel, ze všech ostatních právě dva. Najděte nejrychlejší způsob jak se přepravit mezi koncovými stanicemi.

Řešení

30-2-7 Paměť očima assembleru (15 bodů)

Asi vás při čtení minulého dílu napadlo, že pro spoustu úloh si s třinácti 32-bitovými registry nevystačíme. Pojďme se naučit pracovat s pamětí – té máme obvykle k dispozici řádově gigabajty.

Co je paměť vlastně zač?

V běžných programovacích jazycích většinou přistupujeme k paměti prostřednictvím proměnných, polí, objektů atp. Ale to vše jsou jen abstrakce poskytované naším překladačem či interpretem.

Z pohledu procesoru je paměť prostě dlouhá řada okének, každé z kterýchž si pamatuje jeden bajt, tedy číslo od 0 do 255. Těmto okénkům se občas říká paměťové buňky. Každé okénko je jednoznačně určené svým pořadovým číslem, kterému říkáme adresa.

Pro začátek řekněme, že adresy mají rozsah od 0 do N-1, kde N je velikost paměti v bajtech. Časem se ukáže, že situace je o malinko složitější.

Přístup k paměti

ARM patří mezi takzvané load/store architektury. To znamená, že většina instrukcí neumí přímo pracovat s pamětí, pouze s registry. Namísto toho existují speciální instrukce sloužící k přenosu dat z paměti do registrů (kde s nimi pak můžeme provádět nějaké výpočty) a z registrů do paměti.

Začneme tím nejjednodušším: čtením a zápisem jednoho bajtu. K tomu slouží instrukce:

• LDRB cílový-registr, zdrojová-adresa (LoaD Register Byte) pro čtení z paměti do registru,
• STRB zdrojový-registr, cílová-adresa (STore Register Byte) pro zápis z registru do paměti.

Registr se zapisuje, jak jste zvyklí, např. r3. Adresu lze zapsat vícero způsoby, ale překvapivě ne jako číselnou konstantu. Asi nejjednodušší zápis je [registr], který použije jako adresu obsah nějakého registru.

Takže například instrukce LDRB r1, [r5] načte do registru r1 bajt z adresy uložené v registru r5. Obdobně následující posloupnost instrukcí zapíše bajt s hodnotou 42 na adresu 0x10000:

MOV  r0, #42
MOV  r1, #0x10000
STRB r0, [r1]

Pozor je třeba dát na to, že přístup k paměti je výrazně pomalejší než práce s registry – zhruba 3× až 100×. Proč tak velké rozpětí by bylo na delší povídání – souvisí to s takzvanou cache procesoru, o které možná bude řeč v některém z dalších dílů. Zjednodušeně lze říct, že opakovaný přístup k částem paměti, ke kterým jste přistupovali nedávno, bude rychlejší.

Každopádně se vyplatí hodnoty, se kterými provádíte spoustu výpočtů za sebou, držet v registrech a do paměti uložit třeba až na samém konci nějaké série výpočtů, kdy potřebujete registr uvolnit pro jiné účely.

Paměťová reprezentace čísel

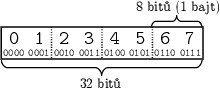
Když registry i aritmetické operace pracují s 32-bitovými čísly, hodilo by se nám tato čísla ukládat do paměti. Do jednoho bajtu se vejde 8 bitů, takže k uložení jednoho čísla potřebujeme 4 bajty. Uvažujme například číslo 0x1234567. To můžeme rozdělit na bajty následovně:

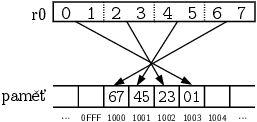
Existují dva běžné způsoby, jak takové číslo do paměti uložit, které se liší pořadím těchto bajtů v paměti. Big endian znamená uložení bajtů v pořadí od nejvýznamnějšího po nejméně významný, jak by je asi přirozeně zapsal člověk. little endian znamená pořadí přesně opačné, tedy naše číslo by bylo zapsané sekvencí bajtů 0x67 0x45 0x23 0x01. Na ARMu se obvykle používá právě little endian (stejně jako na intelských procesorech).

A přestože by se dalo číslo uložit a načíst vhodnou kombinací STRB/LDRB a aritmetických instrukcí, je to natolik běžná operace, že pro ni ARM nabízí speciální instrukce: STR registr, adresa a LDR registr, adresa. Význam parametrů je stejný jako u bajtových verzí, k uložení čísla se použijí paměťové buňky adresa až adresa + 3.

Pokud se v r0 nachází číslo 0x1234567 a provedeme instrukce:

MOV r1, #0x10000
STR r0, [r1]

Je dobrým zvykem ukládat čísla na adresy, které jsou násobkem velikosti daného typu – v tomto případě násobkem čtyř.

Existují i další varianty load/store instrukcí. Kompletní přehled ukazuje následující tabulka:

Úkol 1 [1b]

Vysvětlete, proč zatímco LDRB a LDRH mají znaménkovou a bezznaménkovou variantu, LDR a všechny store instrukce jsou společné pro znaménková i bezznaménková čísla.

Proměnné a paměťové reprezentace

Ve vyšších programovacích jazycích jsme zvyklí pracovat i s jinými typy, než jen čísly. Ukážeme si, jak různé typy reprezentovat v paměti. Paměťovou reprezentací nějakého typu rozumíme schéma určující, jak převést libovolnou hodnotu daného typu na posloupnost bajtů v paměti (a zpět). Reprezentace obvykle mají pevnou velikost, abychom si pro ně mohli vyhradit místo v paměti.

Proměnná pak je prostě vyhrazený úsek paměti obsahující hodnotu proměnné uloženou dle paměťové reprezentace dané typem proměnné.

• Celá čísla jsou reprezentována 1 až 4 bajty, jak bylo popsáno výše, dle potřebného rozsahu. Velikost reprezentace je neměnná: udává maximální číslo, které daná proměnná může uchovat. Ale pokud do 32-bitové proměnné uložíte třeba jedničku, stále bude zabírat v paměti 4 bajty.
• Desetinná čísla se ukládají v takzvaném formátu s plovoucí čárkou (floating-point, IEEE 754). Čísla se ukládají ve tvaru m·2^e, kde čísla m (tzv. mantisa) a e (exponent) jsou uložena zvlášť a každému je vyhrazen nějaký počet bitů. Díky tomuto zápisu mají floatové typy obrovský rozsah, ale omezenou přesnost.

  Existuje několik variant, které se liší velikostí, nejčastěji potkáte takzvanou double precision (typ double v Céčku), která zabírá 64 bitů, z toho 53 bitů tvoří mantisa a 11 exponent. Díky tomu umožňuje reprezentovat čísla v rozsahu řádově od -2¹⁰⁰⁰ do 2¹⁰⁰⁰, ale pamatuje si jen 53 nejvýznamnějších dvojkových číslic. Práce s desetinnými čísly je na ARMu trochu komplikovanější a v seriálu se jí věnovat nebudeme.

• Pole vytvoříme tak, že prostě uložíme spoustu reprezentací daného typu těsně za sebe. Například pole 32-bitových celých čísel o ℓ prvcích bude souvislý úsek paměti délky 4ℓ. Tady je důležité, že reprezentace jednotlivých prvků mají pevnou velikost. Díky tomu dokážeme spočítat v konstantním čase vzdálenost libovolného prvku od začátku pole (tzv. offset, a tedy i jeho adresu. V našem příkladu má i-tý prvek offset 4i a nachází se na adrese A+4i, kde A je adresa začátku pole. ARM navíc nabízí užitečné zkratky pro přístup k prvkům pole, které si ukážeme níže.
  

  Abychom si pro ně mohli vyhradit místo v paměti, musí mít pole pevnou nejen velikost jednoho prvku, nýbrž i počet prvků.

  Občas by se nám ale hodilo mít pole s proměnlivým počtem prvků. Pokud známe nějakou rozumnou horní hranici na to, kolik prvků v poli nejvýše bude, můžeme si v paměti vyhradit prostor odpovídající tomuto limitu (obvykle nazývanému kapacita pole) a pak z něj využít jen aktuálně potřebnou část. To typicky znamená, že si někam vedle uložíme počet prvků, které jsou v poli opravdu uložené (k), potom prvních k prvků pole obsahuje smysluplné hodnoty a zbytek ignorujeme.

  Alternativně můžeme konec obsazené části pole poznat tak, že si za něj přidáme nějakou speciální značku, která se v normálních datech nevyskytuje, například 0 nebo -1.

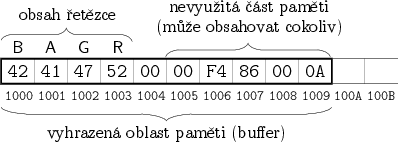
• Řetězce můžeme chápat prostě jako pole znaků, ať už „znak“ znamená cokoli. Pokud se obejdeme bez diakritiky, můžeme znaky reprezentovat ASCII kódy a každý znak zabere jeden bajt. Povídání o tom, jak zacházet s unicodovými řetězci, by vydalo na samostatný seriál.

  U řetězců opět narážíme na to, že mohou mít proměnlivou délku. Zde je nejčastějším řešením (vycházejícím z Céčkové tradice) ukončit platnou část řetězce nulovým bajtem. Například řetězec obsahující slovo BAGR by mohl vypadat následovně:

  
• Struktury a objekty reprezentujeme podobně jako pole, tedy prostě nasázíme do paměti jednou položku za druhou, jen tentokrát může mít každá jiný typ a velikost. Ale protože seznam položek, jejich typy i pořadí jsou pevné a dopředu známé, můžeme opět snadno spočítat offset každé položky od začátku struktury. Ten je neměnný, můžeme si ho klidně spočítat s tužkou a papírem a napsat do programu jako konstantu (v kompilovaných jazycích tohle udělá překladač).

  Ještě je třeba dát pozor na jednu věc. V minulém dílu jsme zmiňovali, že je vhodné, aby číselné typy byly v paměti zarovnané na násobek své velikosti (některé verze ARMu to dokonce vyžadují). Proto se občas mezi prvky struktury nechává vhodně velká mezera (padding), aby následující prvek byl správně zarovnaný. Příklad struktury, která obsahuje 32bitové, 16bitové a znovu 32bitové číslo (v Céčku bychom zapsali jako struct s { int a; short b; int c; }):

  
  V takovéto struktuře víme, že 3. položka bude mít vždy offest 8, takže pro přístup k ní stačí přičíst 8 k adrese začátku struktury. Aby nám zarovnání správně vyšlo, je třeba i začátek struktury mít zarovnaný na násobek čtyř.
• Ukazatele či reference (např. vzájemné odkazy mezi prvky spojového seznamu či vrcholy binárního stromu) ukládáme prostě jako 32-bitové číslo obsahující adresu cíle (kterým je často nějaká struktura). Níže si ukážeme příklad reprezentace spojového seznamu. Null pointer („ukazatel nikam“) reprezentujeme číslem 0. To znamená, že na adresu 0 bychom neměli nic ukládat, protože ukazatel na takovou věc by nešlo rozpoznat od null pointeru. Ale to vám operační systém ani nedovolí.

Pole a režimy adresování

Pojďme se nyní pozorněji podívat na to, jakými způsoby se dá zapsat adresa v load/store instrukcích. Tři základní varianty jsou následující:

• [registr], např. [r4] – adresou je obsah registru. Tento zápis už jsme potkali výše.
• [registr,#konstanta], např. [r2,#10] – jako adresa se použije součet obsahu registru a číselné konstanty (může být i záporná).
• [registr,registr], např. [r2,r7] – jako adresa se použije součet hodnot obou registrů.
• [registr,registr,LSL #posun] – k hodnotě prvního registru se přičte hodnota druhého registru posunutá o daný počet bitů doleva, tedy vynásobená 2^posun. Například [r3,r2,LSL #3] odpovídá adrese r3 + 2³·r2= r3 + 8·r2.

Varianta s konstantním posunem se hodí, když máme spoustu číselných proměnných. Pokud je máme v paměti blízko sebe, nemusíme si před každým čtením nějaké proměnné připravit do registru její přesnou adresu. Místo toho si v jednom registru budeme udžovat začátek celé oblasti a k jednotlivým proměnným přistupovat pomocí tohoto registru a různých offsetů. Například pokud máme číselné proměnné na adresách 0x10000, 0x10004, 0x10008, …, uložíme si např. 0x10000 do r10 a pak k jednotlivým proměnným přistupujeme instrukcemi typu LDR r1, [r10, #8].

Taktéž se hodí pro přístup k položkám struktur: pokud máme v r0 adresu struktury a chceme přistoupit k její položce s offsetem 10, můžeme použít LDR r5, [r0, #10].

Dvouregistrové adresování, zvlášť ve verzi s bitovým posunem, se naopak hodí pro práci s poli. Například máme-li v r0 adresu pole a v r1 index, můžeme příslušný prvek přečíst pomocí LDR r5, [r0, r1, LSL #2].

Následující kód projde pole 32-bitových čísel bez znaménka začínající na adrese 0x10000 o 1024 prvcích a vypíše index maximálního prvku:

MOV r0, #0x10000
MOV r1, #0  // index při procházení
MOV r2, #0  // prozatímní maximum
MOV r3, #-1 // index prozatímního maxima
smycka:
  LDR r4, [r0, r1, LSL #2] // načte prvek pole
                           // z adresy r0 + 4*r1
  CMP r4, r2
  BLO neni_vetsi
    // pokud je větší nebo rovno...
    MOV r2, r4 // ...nahradíme maximum...
    MOV r3, r1 // ...a uložíme jeho index
  neni_vetsi:
  ADD r1, #1
CMP r1, #1024
BLO smycka
// na konci je v r3 index maxima

Z toho, jak fungují pole, vidíme, proč musí mít pevnou velikost. Poté, co si pro pole najdeme nějaké místo v paměti, můžeme přidávat prvky maximálně tak dlouho, dokud konec pole nenarazí na začátek něčeho jiného, co je v paměti uložené o kus dál.

ARM má ještě nabízí ještě další nezvyklé adresovací módy, které usnadňují procházení polí:

• [registr,offset]! – použije registr+offset jako adresu pro load/store instrukci a na konci ji zapíše zpátky do registru.
• [registr],offset – použije hodnotu registru jako adresu pro load/store instrukci a po jejím provedení do něj zapíše hodnotu registr+offset.

Offset může opět být konstanta, další registr nebo registr s posunem. Tyto instrukce se chovají trochu podobně jako Céčkový prefixový a postfixový operátor ++. Použitím těchto adresovacích módů můžeme jednou instrukcí přečíst prvek z pole a skočit na další, ušetříme si tak jednu instrukci ADD.

Ukážeme si to na příkladu kódu, který sečte všechny prvky pole (opět od 0x10000 délky 1024):

MOV r0, #0x10000
MOV r2, #0
smycka:
  LDR r1, [r0], #4
  ADD r2, r1
CMP r0, 0x10400 // pokud je r0 před koncem pole
BLO smycka

Úkol 2 [3b]

V paměti na adrese 0x10004 máte pole 32-bitových celých čísel a na adrese 0x10000 32-bitové celé číslo udávající jeho délku. Vaším úkolem je toto pole obrátit pozpátku na místě (aby se na místě prvního prvku ocitl poslední, …, až na místě posledního první). Ideálně byste se měli obejít bez další pomocné paměti.

Úkol 3 [3b]

V registru r0 dostanete číslo N. Napište program, který vynuluje souvislý blok N bajtů v paměti začínající od adresy 0x10000. Program smí celkem provést nejvýše 0.3·N instrukcí (plus konstanta nezávislá na N).

Úkol 4 [5b]

V paměti na adrese 0x10004 máte pole 32-bitových celých čísel se znaménkem a na adrese 0x10000 32-bitové celé číslo udávající jeho délku (můžete předpokládat, že je to mocnina dvojky). Vaším úkolem je toto pole setřídit. Pro plný počet bodů implementujte nějaký efektivní třídící algoritmus (s lepší než kvadratickou složitostí).

Můžeme doporučit např. nerekurzivní (bottom-up) variantu MergeSortu popsanou v naší kuchařce, případně vhodně implementovaný RadixSort. Máte k dispozici pomocnou paměť velkou jako původní pole (plus nějaká konstanta) od adresy 0x8000000. Výsledné setříděné pole můžete uložit buď místo původního, nebo do této pomocné oblasti.

Příklad: spojové seznamy

Podíváme se na příklad trochu složtější datové struktury, totiž (jednosměrného) spojového seznamu. Ten ve vyšších programovacích jazycích obvykle reprezentujeme jako spoustu struktur (objektů) provázaných ukazateli.

S tím, co jsme si ukázali výše, už víme, jak tyto struktury reprezentovat. Např. bude-li náš seznam obsahovat 32-bitová čísla, bude každý jeho prvek reprezentován souvislým osmibajtovým úsekem paměti. První čtyři bajty budou obsahovat hodnotu prvku, druhé čtyři bajty adresu následujícího prvku.

Poslední prvek má místo adresy následovníka uložen null pointer, tedy nulu.

Na obrázku vpravo je příklad spojového seznamu obsahujícího dvě čísla, 0xAABBCCDD a 0x11223344. Připomínáme, že prvky seznamu mohou být v paměti rozmístěné naprosto libovolně: s mezerami, pozpátku, napřeskáčku, etc.

Následujcí kód projde seznam a spočítá jeho délku. První prvek seznamu je uložen na adrese 0x10000.

MOV r0, #0x10000
MOV r1, #0
smycka:
ADD r1, #1
LDR r0, [r0, 4] // na pozici r0+4 je ukazatel
                // na následující prvek
CMP r0, 0
BNE smycka
// v r1 je délka seznamu

Úkol 5 [3b]

V paměti na adrese 0x10000 máte uložený ukazatel na první prvek spojového seznamu (pozor, nikoli přímo první prvek). Seznam obsahuje 32-bitová celá čísla setříděná ve vzestupném pořadí. V registru r0 dostanete adresu nového prvku – kompletní struktury včetně zatím nevyplněného odkazu na následníka. Vaším úkolem je připojit nový prvek na správné místo do původního seznamu, aby zůstal setříděný a aby na adrese 0x10000 stále byl ukazatel na jeho začátek.

Příklad: vyhledávání v telefonním seznamu

Máme v paměti pole struktur popisující něco jako telefonní seznam. Každá položka obsahuje dva řetězce: jméno (osmibajtový buffer pro řetězec proměnlivé délky ukončený nulovým bajtem) a číslo (4-znakový řetězec pevné délky bez ukončení). Jednoduchý seznam o dvou položkách by mohl v paměti vypadat takto:

Na obrázku pro přehlednost ukazujeme znaky místo jejich ASCII kódů. „\0“ značí nulový bajt (konvenční zápis z Céčka). Odpovídající Céčková deklarace by vypadala takto:

struct polozka {
  char jmeno[8];
  char cislo[4];
};
struct polozka seznam[2];

V registru r0 dostaneme ukazatel na řetězec se jménem, ke kterému bychom chtěli v seznamu najít odpovídající číslo. O to se postará následující kus kódu:

// r0 - vyhledáváný řetězec
// r1 - adresa začátku pole
// r2 - počet záznamů
// r3 - adresa aktuálně zkoumaného záznamu

MOV r3, r1
MOV r10, #12
MUL r10, r10, r2
ADD r10, r1
// r10 = r1 + 12*r2 (adresa konce pole)

porovnej:
// Porovná řetězce na adresách r0 (hledaný)
// a r3 (aktuální jméno v seznamu). Skočí
// na label "stejne" nebo "ruzne" podle výsledku

MOV r4, #0
znak: // porovnání r4-tého znaku obou řetězců
LDRB r5, [r0, r4] // znak hledaného řetězce
LDRB r6, [r3, r4] // znak jména ze seznamu
CMP r5, r6
BNE ruzne
CMP r5, 0
// narazili jsme na konec řetězce, aniž bychom
// předtím našli neshodu
BEQ stejne
ADD r4, #1
CMP r4, #8
BHS ruzne // řetězec neukončený nulou - chyba
B znak

ruzne:
ADD r3, #12 // přejdeme na další záznam
CMP r3, r10
BLO porovnej
B nenalezeno

stejne: // našli jsme shodující se jméno
ADD r3, #8 // o 8 bajtů dál je číslo
// tady bychom ho mohli třeba vypsat, kdybychom
// to uměli

nenalezeno:

Při porovnávání je třeba dát si pozor, abychom se zastavili, když libovolný z řetězců skončí (narazíme na nulový bajt). Protože zbytek bufferu za koncem řetězce může být vyplněný nějakým náhodným smetím, pokud bychom neskončili, mohli bychom dva shodné krátké řetězce vyhodnotit jako různé, protože se liší v této ignorované části.

V kódu výše je to trochu schované: pokud jsou řetězce různě dlouhé a narazíme na konec jednoho z nich, porovnávání skončí, protože se na daném místě znaky liší (jeden řetězec obsahuje nulový bajt a druhý smysluplný znak). Pokud jsou oba řetězce stejně dlouhé, narazíme na oba nulové bajty současně a pomůže nám podmínka CMP r5, 0.

Ale zrovna tak je dobré si pohlídat i maximální délku, pokud by se někde nedopatřením objevil řetězec neukončený nulou, aby porovnávání nepokračovalo donekončena (případně do doby, než narazí na nulu v úplně nesouvisející části paměti).

Paměťová reprezentace instrukcí

Paměť kromě dat, které si tam uložíme, osahuje také kód našeho programu. Tomuto principu se říká von Neumannnova architektura: kód je uložený ve stejné paměti jako data, není pro něj vyhrazené žádné speciální místo. To má spoustu výhod: pokud operační systém načítá kód programu z disku do paměti, může použít stejné instrukce pro práci s pamětí jako pro data (v tuto chvíli ten kód jsou pro něj data). Občas se taky programu může hodit generovat části svého kódu až za běhu.

Jak už jsme naznačili v minulém dílu, program není v paměti uložen jako textový zápis v assembleru, tomu by procesor nerozuměl. Místo toho je každá instrukce (včetně svých parametrů) zakódovaná jedním 32-bitovým celým číslem. Tohle je jedna z vlastností, která činí ARM příjemně jednoduchým; na jiných procesorech mají často různé druhy instrukcí různě dlouhé kódy. Instrukce musí být v paměti zarovnané (uložené na adresách, které jsou násobkem čtyř).

V procesoru existuje speciální registr označovaný pc (Program Counter, dostupný též jako r15), který obsahuje paměťovou adresu aktuálně vykonávané instrukce. Velmi zjednodušeně bychom si činnost procesoru mohli představit jako neustálé opakování následujících kroků:

1. Načti instrukci z adresy pc v paměti
2. Dekóduj a proveď instrukci
3. Pokud instrukce nezměnila pc (neprovedla skok), zvyš automaticky pc o 4 (přejdi na následující instrukci).

Skutečnost je o dost složitější, protože procesor například zpracovává několik instrukcí částečně paralelně (zatímco se jedna provádí, další už se načítá atp.). To má občas trochu podivné důsledky. Například pokusíte-li se přečíst hodnotu registru pc instrukcí typu MOV r0, pc, neuloží se do r0 adresa této instrukce MOV, jak by možná člověk čekal, nýbrž hodnota o 8 vyšší (o 2 instrukce dál).

Podívejme se nyní, jak takový kód nějaké instrukce vypadá. Existuje několik různých kódování pro různé druhy instrukcí: jedno pro všechny aritmetické, jedno pro load/store, jedno pro skoky, atd.

Ukážeme si například kódování aritmetických instrukcí (používané i pro další podobné instrukce, jako např. MOV):

Podíváme-li se na kód instrukce, najdeme v něm:

• Podmínku. Už v minulém díle jsme stručně zmiňovali, že podmínku jde připojit k většině instrukcí, nejen ke skoku. Daná instrukce se pak provede, pouze pokud je podmínka splněná. Každá podmínka z minulého dílu má svůj 4-bitový kód, např. 0000=EQ, 0010=HS, …Existuje speciální podmínka AL (ALways, 1110), která zařídí nepodmíněné spuštění dané instrukce. Ale v assemblerovém zápisu ji lze vynechat (píšeme MOV místo MOVAL).
• Typ druhého argumentu („T“ v diagramu výše). Pokud T=1, druhý argument je konstanta, jinak je to registr.
• Kód operace (opkód), který říká, o jakou instrukci vůbec jde. Např. ADD=0100, MOV=1101.
• Bit S udávající, zda se dle výsledků má nastavit stavový registr. Tímto jsou odlišeny například instrukce ADDS a ADD.
• Číslo registru, který tvoří první argument. Prvním argumentem musí být vždy registr. Číslo registru je přesně to, které je obsažené v jeho názvu – např. r5 je reprezentován číslem 5 (0101).
• Číslo cílového registru, kam se uloží výsledek operace.
• Druhý argument (registr nebo konstanta).

Pravděpodobně jste při hraní s naším simulátorem narazili na to, že některé konstanty nejde v assembleru zapsat (překladač si stěžuje, že jsou příliš velké). Teď už víte proč: na konstantní argument v instrukci zbývá jen 12 bitů, takže tam určitě libovolné 32-bitové číslo nevtěstnáme.

Autoři ARMu ale těchto 12 bitů využili velmi chytře. Namísto jednoho 12-bitového čísla (s rozsahem 0 až 4096) je rozdělili na dvě části: 8-bitovou hodnotu (x) a 4-bitovou rotaci (r). Hodnota druhého operandu vznikne jako x doplněné nulami zleva na 32 bitů a následně bitově zrotované doprava o 2r bitů. Pro r ≥ 4 se tato rotace chová jako bitový posun doleva (rozmyslete si). Takže takto dokážeme snadno vytvářet konstanty tvaru x·2^k pro malá x.

Filip Štědronský

Řešení