KSP-H	1. série se opravuje, 2. sérii odevzdávejte do 15. 12. 2024
KSP-Z	1. série opravena, 2. sérii odevzdávejte do 8. 12. 2024

Čtvrtá série třicátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

30-4-1: Černobílé hádání
30-4-2: Kočka na stromě
30-4-3: Hippocoin
30-4-4: Malování 2.0
30-4-5: Frňákovník
30-4-6: Takřka nudná úloha
30-4-7: Překřikující se procesory

30-4-1 Černobílé hádání (Zadání)

Cílem je nalézt rozumně dobrou strategii pro zjištění, kde jsou bílá a černá políčka v poli, do kterého nemáme přístup. Můžeme se nicméně ptát, zda je v nějakém úseku aspoň jedno políčko černé/bílé, tedy o úseku zjistit, jestli je čistě černý, čistě bílý, anebo míchaný.

Úlohu můžeme samozřejmě vyřešit postupným položením N dotazů a pokud bychom o poli nic nevěděli, byla by to i optimální strategie. Máme ale slíbeno, že pole bude tvořeno jednobarevnými úseky a bude jich řádově méně než celkový počet políček. Mohli bychom binárně vyhledávat konec každého úseku – testovat jednobarevnost intervalů začínajících na konci předchozího úseku. Tak dostaneme za řádově log N dotazů přesnou informaci o tom, kde jeden úsek končí, a když to uděláme pro každý z M úseků, tak celé pole projdeme za O(M log N).

Trochu detailněji popsáno: Při binárním vyhledávání začneme dotazem v polovině, tedy dotazem na interval [0, N/2]. Tím zjistíme, jestli je konec v první nebo druhé půlce pole. Pak postup opakujeme pro tu polovinu, kde má být konec – například [0, 3/4 · N], kdybychom prvním dotazem zjistili, že interval je jednobarevný a konec v první půlce není. Abychom otestovali jednobarevnost úseku, tak se můžeme zeptat na první políčko (jedním dotazem „je úsek [0, 0] bílý?“) a pak nám pro každý další stačí zjistit, jestli má stejnou barvu, jako ten první (např. dotazem „je úsek [0, X] bílý?“). Až takto najdeme, jak je velký první jednobarevný úsek, tak se můžeme pustit do druhého. Protože ten první úsek už nebudeme potřebovat, můžeme jeho barvu vypsat a „zapomenout“, že tam něco bylo – snížíme si M o jedna, N o délku prvního úseku a všechny následující dotazy budeme posílat posunuté o délku prvního úseku.

Celkem použijeme přinejhorším O(M log N) dotazů, v každé iteraci jeden na zjištění barvy a log N na dohledání konce. Žádné složité výpočty mimo dotazování neprovádíme, časová složitost bude také O(M log N) (pokud vypisujeme pole po skupinách; kdybychom ho vypisovali po dílkách, dostaneme časovou složitost O(N + M log N)). Za povšimnutí také stojí, že pokud budeme výstup rovnou vypisovat, nepotřebujeme alokovat žádnou paměť, kromě konstantního množství proměnných.

Standa Lukeš

30-4-2 Kočka na stromě (Zadání)

Nefunkční řešení

Na první pohled to může vypadat, že by mohly jít najít dvě nejkratší cesty „postupně“ – najdu jednu nejkratší cestu a potom druhou v grafu bez vnitřních vrcholů té první. Takové řešení se ale rozbije například na grafu na obrázku. I přesto, že dvě cesty mezi nimi existují, první hledání nejkratší cesty by mohlo najít cestu, jejíž odstranění z grafu vrcholy úplně odstřihne.

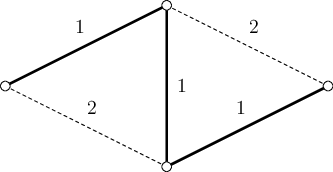
Funkční řešení

Mohli jste si všimnout, že úloha je kuchařková a kuchařka je o tocích v síti, takže asi nebude špatný nápad toky použít. V kuchařce je dokonce popsáno, jak najít dvě (hranově) disjunktní cesty, jenom ta cesta nemusí být nejkratší. Mohli bychom ale pomocí trochu modifikovaného Dijkstrova algoritmu vyrobit graf, kde všechny cesty budou nejkratší – nebude tam žádná delší cesta než nejkratší cesta mezi hasiči a kočkou. Pak v tomto grafu všechny hrany ohodnotíme jedničkou a najdeme největší tok. Když bude velký alespoň 2, tak v něm najdeme dvě cesty mezi hasiči a kočkou a obě budou nejkratší.

Abychom vyrobili orientovaný graf se samými nejkratšími cestami, prohledáme mapu skoro-Dijkstrovým algoritmem a skončíme, až když vzdálenost převýší vzdálenost kočky (ne hned, jak k ní dojdeme, jako bychom dělali běžně). Když prohledávání zastavíme až po překročení vzdálenosti, máme jistotu, že tam už žádná další nejkratší cesta není.

Během průběhu si navíc budeme psát, přes jaké hrany se dá do každého vrcholu dostat. Když narazíme na alternativní nejkratší cestu do vrcholu, tak ji přidáme do seznamu. Delší cesty tam nepřidáváme. Do výsledného grafu zahrneme jen hrany, které jsme si při prohledávání poznamenali, a ať v něm půjdeme po orientovaných hranách ke kočce jakoukoli cestou, bude nejkratší, protože žádné hrany, které by cestu mohly prodloužit, jsme do grafu jednoduše nepřidali. Na obrázku vidíte co tato transformace udělala s grafem z prvního obrázku. Tentokrát jsou tam všechny hrany, ale to je spíše náhoda.

Pročištěný graf: hrany na nejkratších cestách

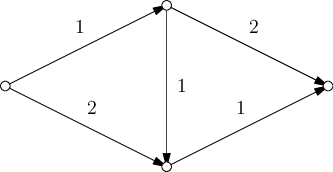
Teď potřebujeme najít nejlepší tok v síti s průtokem maximálně 1 ve všech hranách a vrcholech. Drobný problém je, že Fordův-Fulkersonův algoritmus z kuchařky umí limitovat jen průtok v hranách, ne ve vrcholech. To ale obejdeme jednoduchým trikem – nahradíme každý vrchol dvěma vrcholy spojenými hranou s kapacitou 1. Všechny vstupní hrany dáme do prvního vyrobeného vrcholu a všechny výstupní do druhého. Takto nám vrcholem poteče maximálně 1. Na obrázku je příklad takového převedeného grafu.

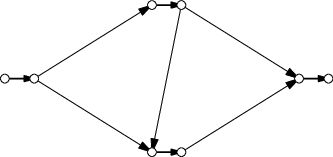
Když máme tok, tak podle něj jenom najdeme cestu, jako je to popsané v kuchařce. Jednoduše půjdeme (projdeme prohledáním do hloubky) jednou cestou, kudy teče tok, a pak půjdeme druhou cestou, kde teče.

Rychlé řešení

Toto řešení funguje a doběhne v polynomiálním čase, ale hledání maximálního toku docela trvá. Můžeme ovšem využít faktu, že nepotřebujeme maximální tok, nýbrž nám stačí jen nějaký tok velikosti 2 (nebo informace, že neexistuje). Fordův-Fulkersonův algoritmus běží v krocích, v každém kroku najde prohledáním grafu do šířky zlepšující cestu, a protože jsou všechny kapacity 1, každá zlepšující cesta zlepší tok o 1. Standardní algoritmus se zastaví, až když žádnou další zlepšující cestu nenajde, což nemusí být zrovna brzy. My ho ale můžeme zastavit už po dvou krocích, tok velikosti 2 nám na dvě paralelní cesty bohatě stačí.

Na celý algoritmus tak potřebujeme prohledat graf podobně, jako to dělá Dijkstrův algoritmus, což zabere O(M log N) času. Pak vyrobíme tokovou síť, to stihneme v lineárním čase. Na tokové síti najdeme dvakrát zlepšující cestu prohledáním do šířky, takže to také bude trvat lineárně dlouho. Nakonec v nalezeném toku najdeme dvě cesty, opět to nebude problém stihnout v lineárním čase nějakým prohledáním grafu. Takže ve výsledku jsme se dostali na stejný čas, jako má Dijkstrův algoritmus – O(M log N).

Standa Lukeš

30-4-3 Hippocoin (Zadání)

Nejprve provedeme několik jednoduchých pozorování. Uvědomíme si, že pokud chceme obchodovat, vždy se vyplatí využít všechny peníze (ať už koruny, nebo hippocoiny), které máme. Buď se totiž jedná o nějakou transakci, která je pro nás výhodná, a je tedy dobré investovat vše, a nebo nevýhodná, kterou je lepší vůbec neuskutečnit. Dále si uvědomíme, že je výhodné nakupovat hippocoiny těsně před tím, než nákupní cena začne růst, a prodávat je těsně před tím, než prodejní cena začne klesat (takové body se nazývají lokální minimum, respektive maximum). Pokud bychom totiž hippocoiny chtěli koupit dříve (za stejnou nebo vyšší cenu), stejně bychom s prodejem museli počkat na růst nákupní ceny, abychom je mohli výhodně prodat (za vyšší cenu, než jsme je koupili), protože prodejní cena je vždy menší nebo rovna nákupní. Naopak pokud bychom hippocoiny chtěli kupovat později, jednak bude nákupní cena vyšší, jednak se zdržením můžeme připravit o možnost výhodného prodeje.

Jednoduchá varianta

Řešením jednoduché varianty je algoritmus, který v každém minimu hippocoiny nakoupí a v každém maximu je prodá. Stačí jednou projet celou posloupnost a řídit se podle následujících dvou podmínek:

Pokud další den cena poroste, nakup za všechny peníze hippocoiny.
Pokud další den cena klesne nebo je poslední den, prodej všechny hippocoiny.

Dokázali jsme, že se nevyplatí obchodovat jinde než v minimech, respektive maximech, nyní dokážeme ještě, že se nevyplatí žádné minimum nebo maximum vynechat. Při našem obchodování pravidelně střídáme nákup a prodej. Po každé dvojici transakcí nákup hippocoinů – jejich prodej za vyšší cenu budeme mít víc peněz než před ní. A protože cena v každém maximu je vždy vyšší než cena v předchozím minimu, vyplatí se provést všechny tyto transakce. Popsaný algoritmus je tedy správným řešením s časovou složitostí O(N), protože projdeme posloupnost pouze jednou, a paměťovou složitostí O(1), protože nám stačí pamatovat si cenu v dnešním a v následujícím dni.

Rozšíření na těžkou variantu

Přímočarým řešením těžší varianty by byl stejný algoritmus jako u jednoduššího řešení, který by ovšem bral v úvahu pouze minima z nákupní ceny a maxima z prodejní. To ale nestačí. Jednak se mohou objevit dvě minima v nákupní ceně za sebou, aniž by mezi nimi bylo maximum z ceny prodejní (musíme se tedy rozhodnout, ve kterém minimu chceme nakoupit), jednak maximum prodejní ceny může být menší než minimum nákupní ceny a nemusí se nám vyplatit vždy obchodovat, protože bychom neprodali hippocoiny za vyšší cenu, než jsme je koupili. Budeme si tedy pamatovat poslední transakci (nákup nebo prodej nenulového množství peněz a jeho cenu) a přidáme dvě podmínky:

Pokud chceme provést transakci stejného typu jako předchozí a dnešní cena je výhodnější, zruš poslední transakci a proveď ji až dnes.
Pokud chceme prodat hippocoiny a prodejní cena je nižší než ta, za kterou jsme je nakoupili, prodej neprováděj.

Zbývá nám už jen jedna maličkost – zajistit, že poslední den budeme mít koruny a ne hippocoiny. V lehčí variantě jsme to vyřešili tak, že jsme hippocoiny nakupovali, pouze když jsme věděli, že cena ještě poroste. Tady však nevíme, jestli prodejní cena ještě překročí tu nákupní, proto přidáme poslední podmínku:

Pokud jsme dojeli na konec a poslední transakce je nákup, transakci zruš.

Algoritmus má stejně jako u jednodušší varianty časovou složitost O(N) a paměťovou O(1).

Jiné řešení podle Jirky Škrobánka

Vyjdeme z toho, že pokud známe maximální možný počet korun k_i a hippocoinů h_i, který můžeme i-tý den mít, pak (i+1)-ní den je maximální možný počet korun maximum z k_i (pokud si necháme koruny v korunách) a h_i·p_i+1 (pokud si převedeme včerejší částku v hippocoinech na koruny), kde p_i+1 je prodejní cena hippocoinů (i+1)-ní den.

Na začátku máme dané množství peněz k₀. Pokud si je hned první den převedeme na hippocoiny, získáme h₀. Projdeme celou posloupnost a budeme si vždy pamatovat aktuální k_i a h_i. Jakmile dojdeme na konec, zjistíme nejvyšší počet korun, který můžeme při obchodování během dané doby získat. Pokud chceme znát i postup, jak obchodovat, budeme si muset pamatovat kromě k_i a h_i také to, kdy jsme peníze měnili.

I toto řešení má lineární časovou a paměťovou složitost.

Zuzka Urbanová

30-4-4 Malování 2.0 (Zadání)

Před samotným hledáním algoritmu si pojďme projít detaily zadání. Máme pouze dvě barvy, takže o obrázku můžeme uvažovat jako o bitové mapě. Štětec nám barvy pouze prohazuje, nezáleží tudíž na přesném počtu kliknutí na pixel, ale pouze na sudosti a lichosti. Každé dvě aplikace štětce na tomtéž místě se navzájem vyruší. U každého pixelu obrázku se tedy musíme pouze rozhodnout, jestli na něj kliknout, nebo ne. Navíc o štětci můžeme uvažovat jako o binární operaci xor – malování je xorování s jedničkou.

Pokud jde obrázek štětcem namalovat, tak jde určitě i smazat. Stačí ho namalovat podruhé přes sebe sama. Dostaneme tím v každém bodě obrázku dvě aplikace štětce nebo žádnou – celkově žádnou změnu. A naopak: pokud jde smazat, stejný postup aplikovaný na prázdnou plochu ho namaluje.

Pojďme tedy obrázek smazat! Kde ale začít? Podíváme-li se na rohové pixely obrázku, tak každý z nich je možné změnit pouze jedním možným způsobem. Uvažujme pouze o levém horním rohu obrázku. Můžeme aplikovat štětec přímo v rohu, tím se pak barva pixelu změní. Když ale klikneme kamkoliv jinam, tak se pixel akorát dostane mimo dosah. Takže barva levého horního pixelu nám pevně určuje první aplikaci štětce – musíme tam dostat bílou. Akorát při kliknutí musíme změnit barvu celé oblasti k ×k a nejen rohového pixelu. Co dál? Levý horní pixel považujeme za vyřešený, takže na něj již nechceme sahat. Vznikly nám tím dva nové rohové pixely. Vezměme třeba ten vpravo – můžeme ho také změnit pouze jedním způsobem.

Budeme-li takto pokračovat, dostaneme se na konec prvního řádku. Na posledních k-1 pixelů ale nejde přímo kliknout, takže pokud nejsou bílé, tak obrázek smazat nejde. Tím jsme vyřešili první řádek a můžeme to samé opakovat pro další. Posledních k-1 řádků opět nepůjde změnit přímo. Ty opět rozhodují o tom, jestli je obrázek smazatelný. Celý výsledný algoritmus vypadá takto:

Pro každý řádek x:
Pro každý sloupec y:
Když je pixel [x,y] černý:
Když se štětec na [x,y] vejde na obrázek:
Změníme barvu všem políčkům štětce.
Když se nevejde:
Obrázek nejde nakreslit.
Obrázek nakreslit jde.

Jelikož krok 5 trvá O(k²), celková složitost tohoto algoritmu činí O(MNk²). Paměť nám stačí na uložení obrázku, takže O(MN).

To musí jít rychleji!

Proč je předchozí algoritmus pomalý? Při každé aplikaci štětce musíme změnit barvu k² pixelů. Dá se to ale obejít. Protože se jedná o souvislou oblast, můžeme si pomoci 2D intervalovými stromy. Tím bychom místo O(MNk²) dostali složitost O(MN log M log N). To může být lepší v závislosti na velikosti k. Jde to ale ještě rychleji a pomocí méně komplikované datové struktury!

Vezměme si nějaký pixel uvnitř obrázku. Kolikrát mu změníme barvu? Tolikrát, kolikrát jsme ve čtverci vlevo nad ním velikosti k × k použili štětec. Na toto můžeme použít variantu prefixových součtů. U každého pixelu si budeme pamatovat, kolikrát byla jeho barva změněna. Pro pixel na souřadnicích [x,y] říkejme této hodnotě p_x,y. Začínáme s tím, že každý pixel nebyl nikdy prohozen, takže si každý pamatuje nulu. Navíc si u každého pixelu pamatujme, jestli na něj byl použit štětec – hodnotu š_x,y. Ta nabývá hodnot nula nebo jedna.

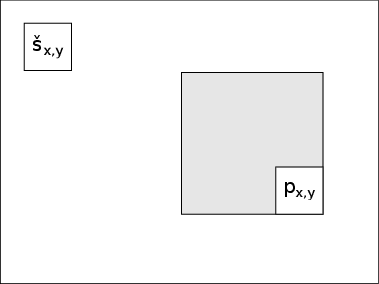
Budeme obrázek opět procházet z levého horního rohu a u každého pixelu se zastavíme a rozhodneme se, jestli na něj potřebujeme použít štětec, nebo ne. Pak spočítáme jeho hodnotu p a uložíme si ji.

Protože krajní vrcholy je potřeba ošetřit speciálně, začněme pro ukázku nějakým vnitřním pixelem obrázku. Řekněme, že leží na souřadnicích [x,y]. Než jsme se k tomuto pixelu dostali, prošli jsme všechny pixely vlevo a nahoře. Takže speciálně máme určitě spočítané hodnoty p_x-1,y, p_x,y-1 a p_x-1,y-1. Kolikrát byla pixelu [x,y] změněná barva? Nejlépe je to vidět asi z následujícího obrázku:

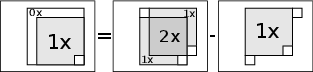
Dostáváme tedy výraz p_x,y = p_x-1,y + p_x,y-1 - p_{x-1, y-1} - š_x-k,
y - š_{x, y-k} + š_{x-k, y-k}, díky kterému jsme schopní hledaný počet prohození barvy konkrétního pixelu spočítat v konstantním čase. Navíc nás nutně nezajímá přesný počet, můžeme vše počítat modulo 2. Takže také víme, jestli je po všech těchto prohozeních pixel bílý nebo černý a můžeme postupovat stejně jako v prvním algoritmu.

Abychom mohli algoritmus dokončit, musíme se ještě vypořádat s případy, kdy chceme číst hodnoty p a š z oblastí mimo obrázek. To můžeme vyřešit velmi jednoduše, mimo hranice obrázku prostě žádné změny dělané nebyly, takže obě hodnoty jsou nulové. Celý algoritmus tedy nakonec vypadá následovně:

Pro každý řádek x:
Pro každý sloupec y:
p_x,y ← (p_x-1,y + p_x,y-1 - p_{x-1, y-1} - š_{x-k, y} - š_{x, y-k} + š_{x-k, y-k}) mod 2
Když je pixel [x,y] černý po p_x,y prohozeních:
Když se štětec vejde na obrázek:
š_x,y ← 1
p_x,y ← 1 - p_x,y
Když se nevejde:
Obrázek nakreslit nejde.
Jinak š_x,y ← 0
Obrázek nakreslit jde.

Výslednou složitost dostáváme nakonec O(MN). Paměťová je stejná, protože v každém pixelu si udržujeme pouze konstantní množství informace – dvě čísla.

Vašek Šraier

Líné přebarvování

Pomalé přebarvování čtverců k×k z našeho prvního řešení jde také zrychlit takzvaným líným vyhodnocováním. Pořídíme si pomocné pole ℓ, ve kterém budou jedničky na místě požadavků na přebarvení: ℓ_x,y=1 bude znamenat, že všechna políčka v „nekonečném čtverci“ od políčka [x,y] doprava a dolů se mají přebarvit. Všimneme si, že přebarvení čtverce k×k s levým horním rohem [x,y] lze provést znegováním požadavků ℓ_x,y, ℓ_x+k,y, ℓ_x,y+k a ℓ_x+k,y+k. To je stejný trik, jako u 2D prefixových součtů.

Dobrá, tím jsme přebarvování odložili na později. Kdo ho ale provede? Dohodneme se, že kdykoliv dojdeme na nějaké políčko [x,y] a leží na něm požadavek, tak tento požadavek vyřešíme zadáním nějakých požadavků na ještě neprojitých políčkách. Konkrétně si uvědomíme, že požadavek ℓ_x,y=1 můžeme vyřídit znegováním samotného políčka [x,y] a požadavků ℓ_x+1,y, ℓ_x,y+1 a ℓ_x+1,y+1.

Zadat požadavek i vyřešit ho tedy dokážeme v konstantním čase, takže celé líně přebarvovací řešení má složitosti O(MN). Mimochodem, všimněte si, že je vlastně docela podobné předchozímu rychlému řešení, jen něco jako prefixové součty počítá pro budoucnost místo minulosti.

Martin „Medvěd“ Mareš

30-4-5 Frňákovník (Zadání)

Jakým nejjednodušším způsobem by se tato úloha dala vyřešit? Můžeme použít hrubou sílu. Vyzkoušíme všechny možné kombinace nádob (je jich 2^N), spočítáme jejich celkový objem, zkontrolujeme dělitelnost sedmi a najdeme maximum. Rychlé to ale nebude, kvůli počtu všech kombinací dostáváme časovou složitost O(2^N ·N) a paměťovou složitost O(N).

Jak bychom to implementovali? Docela se na to hodí rekurze, protože se jí hezky dají generovat ty kombinace. Vezmeme první nádobu dohromady se všemi rekurzivně spočítanými kombinacemi ostatních nádob. Tím dostaneme půlku všech kombinací. Pro druhou půlku první nádobu zahodíme a vezmeme opět rekurzivně všechny možné kombinace zbytku. Abychom si nemuseli kombinace ukládat, můžeme v poslední vrstvě rekurze zkontrolovat součet a hledat maximum. Je potřeba to ale nějak zrychlit!

Jedno drobné vylepšení se hned nabízí. Nemusíme počítat součty až po výběru nádob, můžeme je sčítat již průběžně při rekurzivním generování a předávat si do rekurze součet. Snižujeme tak časovou složitost na O(2^N). Můžeme to ale také celé otočit. Rekurzivní funkce nebude vytvářet kombinace, bude počítat přímo výsledek – největší možný součet objemů nádob dělitelný sedmi. Vezmeme první nádobu a největší součet ze zbylých nádob se zbytkem po dělení sedmi takovým, aby nám nakonec vyšel zbytek nulový. To samé zkusíme s tím, že první nádobu nebudeme započítávat.

V kódu to může vypadat například následovně:

N = 5
nadoby = [2, 3, 2, 2, 17]

def vyber(zacatek, zbytek):
  # vrací celkový objem a seznam nádob

  # když už nejsou nádoby, ukončíme rekurzi
  if zacatek == N:
      return 0, [] # rozbije se pro zbytek != 0

  # tady vyzkoušíme obě varianty součtů
  z = nadoby[zacatek] % 7
  soucet_s, vybrane_s =
    vyber(zacatek + 1, (7 + zbytek - z) % 7)
  soucet_bez, vybrane_bez =
    vyber(zacatek + 1, zbytek)

  # a vezmeme tu lepší
  if soucet_s > soucet_bez:
    return (soucet_s + nadoby[zacatek],
            vybrane_s + [nadoby[zacatek]])
  else:
    return soucet_bez, vybrane_bez

print(vyber(0, 0))

Stále je to ale pomalé. Funkce vyber se spustí řádově 2^N-krát. Jaké ale dostává vstupní parametry? Index do pole s nádobami – těch je N – a zbytek po dělení sedmi – těch je celkem sedm. Takže máme celkem 7N možných způsobů, jak zavolat funkci, ale voláme ji 2^N-krát. To je spousta zbytečné práce! To ji přeci musíme volat se stejným vstupem vícekrát! Pojďme si pořídit cache a ukládejme si do ní předchozí výsledky. Díky tomu nebude potřeba počítat pořád dokola to samé. Sníží nám to časovou složitost na krásných O(N). Zůstává tam ale pořád ta rekurze, kterou z praktických důvodů nechceme mít moc hlubokou (kvůli velikosti zásobníku).

Jak naší cache vyplňujeme? Rekurze se první zanoří do maximální hloubky, spočítá výsledek pro nula nádob, uloží ho do cache a vrátí se o vrstvu výše. S pomocí cache pak spočítáme hodnotu pro jednu nádobu, pro dvě, atd. To ale není nic jiného, než lineární procházení cache odzadu. Takže vlastně rekurzi nepotřebujeme, můžeme to samé spočítat přímo.

Cache má velikost O(7N)=O(N) a můžeme si ji reprezentovat například jako dvourozměrné pole. Obsahuje pro každý počáteční index a zbytek po dělení sedmi objem nejlepšího výběru nádob a odkaz na stav, ze kterého byla tato hodnota vypočítána. Můžeme díky tomu rekonstruovat výběr nádob.

Cache budeme lineárně procházet od posledních nádob. Pro každou nádobu navíc projdeme všechny zbytky po dělení sedmi a z předchozích hodnot dopočteme ještě nespočítané stejně jako při rekurzi. Když je cache plná, tak poslední spočítaná vrstva obsahuje výsledek u zbytku rovného nule. Navíc odkazuje na předchozí použitý stav, takže si z toho umíme spočítat, jestli byla první nádoba použitá nebo ne. Obdobně pro všechny další nádoby.

Ještě si můžeme všimnout jednoho drobného detailu – rekurze cache vyplňuje pozpátku, ale ve výsledku je to úplně jedno. Můžeme průchod otočit a začít od první nádoby, skončit u poslední. Nic to na situaci nezmění.

Vyřešeno tedy máme v čase O(N) a ve stejné paměti. Použitá technika postupného vylepšování rekurzivního řešení spadá pod tzv. dynamické programování. Více se o tomto tématu můžete dočíst v naší kuchařce.

Program (Python 3)

Vašek Šraier

30-4-6 Takřka nudná úloha (Zadání)

Připomeňme si úlohu: máme dvě posloupnosti A a B, obě délky n. Chceme v lineární paměti spočítat jejich nejdelší společnou podposloupnost, tj. vyškrtat z nich co nejméně prvků, aby se zbylé posloupnosti rovnaly.

Jak se píše v zadání, bez požadavku na lineární paměť jde o známou úlohu. Připomeňme řešení z kuchařky o dynamickém programování. Výpočet probíhá v n krocích, v i-tém kroku uvažujeme jen společné podposloupnosti A a B, které v A končí nejpozději na pozici i. Přechod z i-tého do (i+1)-tého kroku probíhá tak, že se podíváme, jak se dosavadní posloupnosti prodlouží, když jim povolíme využít navíc i prvek A[i+1].

Neuvažujeme však všechny podposloupnosti, ale jen ty, které mají potenciál být prodlouženy na nejdelší společnou. V kuchařce je zdůvodněno, že v jednom kroku nám stačí pamatovat si jen jednu podposloupnost od každé délky, a to konkrétně tu, která v B končí co nejdříve. Říkejme takovým podposloupnostem slibné. Navíc si z paměťových důvodů nepamatujeme všech těchto O(n) podposloupností, ale jen jejich poslední prvky, resp. indexy posledních prvků v poli B.

Označme tento index pro slibnou podposloupnost délky ℓ v i-tém kroku jako d_i[ℓ]. Kuchařkové řešení ve své podstatě funguje tak, že se při přechodu k (i+1)-tému kroku podívá na všechny slibné podposloupnosti z i-tého kroku a podívá se, kde by v B nejdříve končily, kdyby se prodloužily o prvek A[i+1]. V praxi to znamená, že se vezme hodnota d_i[ℓ], v B se od ní napravo najde index nejbližšího výskytu prvku A[i+1] a tímto indexem se pokusíme zlepšit hodnotu d_i+1[ℓ+1] (tj. nahradíme ji, právě pokud je nový index menší než současná hodnota).

Každou hodnotu d_i[ℓ] jsme pak mohli získat dvěma způsoby: buď vylepšením z d_i-1[ℓ-1], nebo ponecháním d_i-1[ℓ]. Když si tedy ke každému d_i[ℓ] připíšeme, jak jsme ho získali, jsme schopni zpětně zrekonstruovat nejdelší společnou podposloupnost: najdeme nejvyšší ℓ, pro které je d_n[ℓ] definované, a budeme zpětně následovat „šipky“ a za každý přechod z d_i[ℓ] do d_i-1[ℓ-1] současný prvek přidáme do nejdelší společné podposloupnosti. Označme jako p_i hodnotu ℓ v i-tém kroku podle tohoto postupu rekonstrukce. Všimněte si, že k rekonstrukci nám stačí znát všechna p_i a k nim příslušné hodnoty d_i[p_i] a zbytek pole d_i vlastně nepotřebujeme.

Pomalé řešení

Problém kuchařkového přístupu je, že si kvůli rekonstrukci musíme pamatovat všechna pole d_i. Přímočaré řešení se hned nabízí: Nebudeme si při rekonstrukci pamatovat všechna d_i, ale vždy jen to d_i, které právě potřebujeme. Když pak přecházíme od d_i k d_i-1, zapomeneme pole d_i, načež spustíme celý algoritmus od začátku a zastavíme ho v (i-1)-tém kroku, abychom spočítali pole d_i-1. Takto celkem algoritmus zavoláme O(n)-krát a celková časová složitost bude O(n³).

Zrychlujeme

Začneme pozorováním: kdykoliv jsme v kroku i a máme spočítané pole d_i, jsme schopni v čase O(n(n-i)) a paměti O(n) zjistit hodnotu p_i, tedy zjistit, která ze slibných posloupností v poli d_i se nakonec prodlouží na tu nejdelší. Můžeme si totiž každý prvek d_i pomyslně obarvit a nechat kuchařkový algoritmus postupně spočítat d_i+1, … , d_n, přičemž každé políčko d_j[k] vždy obarvíme barvou políčka, ze kterého získalo svou hodnotu. Na konci se pak jen podíváme na barvu, kterou má nejdelší společná podposloupnost.

Nyní toto pozorování využijeme spolu s radou ze zadání navádějící k použití metody Rozděl a panuj. Spustíme kuchařkový algoritmus a pozastavíme ho v kroku n / 2 (BÚNO je n sudé, jinak zaokrouhlíme dolů) a zapamatujeme si pole d_n/2. Pak algoritmus necháme doběhnout do konce a pomocí výše popsaného postupu zjistíme hodnotu p_n/2.

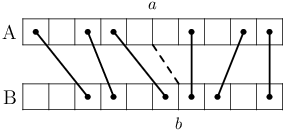
Jak ilustruje obrázek, teď jsme si celý problém rozdělili na dva menší. Označme a = n/2 a b = d_n/2[p_n/2]. Spočítáním p_n/2 jsme nejdelší společnou podposloupnost A a B rozdělili na dvě části: nejdelší společnou podposloupnost A[1… a] a B[1… b] a nejdelší společnou podposloupnost A[a+1… n] a B[b+1… n]. Můžeme tedy rekurzivně vyřešit nejprve levou část a pak pravou. Postupně tak spočítáme všechna p_i a hodnoty d_i[p_i] a z nich už snadnou úpravou původního algoritmu pro rekonstrukci získáme nejdelší společnou podposloupnost.

Jakou má tento algoritmus složitost? Nejprve si rozmyslíme, že jsme se opravdu vešli do lineární paměti. Na začátku si vždy udržujeme nejvýše dvě lineárně velká pole d_*: d_i a d_i+1; později nám k tomu přibude ještě pole d_n/2. Jakmile kuchařkový algoritmus doběhne, stačí nám pamatovat si jen O(1) hodnot: p_n/2 a hodnotu d_n/2[p_n/2]. Rekurze nám analýzu trochu komplikuje, ale stačí si uvědomit, že vždy běží nejvýše jedno rekurzivní volání najednou, které (jak už jsme si rozmysleli) samo o sobě spotřebuje lineárně mnoho pomocné paměti, kterou po svém doběhnutí uvolní. Všechna ostatní aktuálně neběžící volání spotřebovávají jen O(1) paměti a je jich O(n).

Časová složitost vyjde O(n²). Abychom to nahlédli, uvědomíme si, že na jedné úrovni rekurze, kde zkoumáme nějaký úsek A velký a a úsek B velký b, strávíme nejvýše ab jednotek času (Kde jako jednotku času volíme nějakou vhodnou konstantu. Zde musíme na chvíli odložit O-notaci, protože je pro naše potřeby moc hrubá.). To je triviální, protože pouze pouštíme kuchařkový algoritmus na posloupnosti velké a a b a děláme navíc konstantní množství další práce. Celkem tedy na první úrovni strávíme nejvýše n² jednotek času a pak se zavoláme na oba podproblémy, jeden velikosti n/2 a b, druhý velikosti n/2 a n - b. Na těch strávíme nejvýše n/2·b + n/2·(n-b) = n/2·n = n²/2 jednotek času. Z nich se opět zavoláme na ještě menší podproblémy, na kterých dohromady strávíme n/4 ·b₁ + n/4 ·(b - b₁) + n/4·b₂+ n/4·(n - b - b₂) = n²/4 času. Takto to pokračuje dál a celkem za všechna volání můžeme strávený čas odhadnout jako n² + n²/2 + n²/4 + … ≤ 2n² = O(n²) pomocí známého vzorečku pro součet geometrické řady.

Na závěr poznamenáme, že na tento algoritmus přišel v roce 1975 jistý Dan Hirschberg a na jeho počest se algoritmus jmenuje Hirschbergův.

Ríša Hladík

30-4-7 Překřikující se procesory (Zadání)

Úkol 1: Read-write spinlock

Read-write (RW) spinlocky je možné implementovat mnoha způsoby. My si stav RW spinlocku uložíme do jedné 32-bitové proměnné, se kterou budeme zacházet pomocí atomických instrukcí LDREX a STREX. Je-li zámek odemčen, v proměnné bude 1. Je-li zamčen pro zápis, uložíme 0. Pokud ho má zamčeno pro čteni k procesorů, uložíme k+1.

Zamčení pro zápis funguje takto: čekáme, dokud v proměnné nebude jednička, a tu pak atomicky změníme na nulu. Řídíme se volací konvencí, takže parametr s adresou zámku očekáváme v r0.

zamkni_pro_zápis:
  LDREX r1, [r0]
  CMP   r1, #1
  BNE   zamkni_pro_zápis
  MOV   r1, #0
  STREX r2, r1, [r0]
  CMP   r2, #0
  BNE   zamkni_pro_zápis
  BX    lr

Pokud chceme zamykat pro čtení, čekáme, dokud proměnná je nulová, a jakmile přestane být, zvýšíme ji atomicky o 1.

zamkni_pro_čtení:
  LDREX r1, [r0]
  CMP   r1, #0
  BEQ   zamkni_pro_čtení
  ADD   r1, #1
  STREX r2, r1, [r0]
  CMP   r2, #0
  BNE   zamkni_pro_čtení
  BX    lr

Odemčení po zápisu pouze přepíše 0 na 1. Jelikož víme, že v tomto okamžiku máme k zámku exkluzivní přístup, nemusíme používat STREX, stačí nám vědět, že zápis jednoho slova do paměti je atomický.

odemkni_po_zápisu:
  MOV   r1, #1
  STR   r1, [r0]
  BX    lr

Odemčení po čtení musí proměnnou snížit o 1, a to už je potřeba provádět atomicky:

odemkni_po_čtení:
  LDREX r1, [r0]
  SUB   r1, #1
  STREX r2, r1, [r0]
  CMP   r2, #0
  BNE   odemkni_po_čtení
  BX    lr

Nevýhodou tohoto řešení je, že pokud nějaký procesor chce zapisovat, čtoucí procesory ho mohou neomezeně dlouho blokovat: Představte si, že jeden procesor chce zapisovat a mnoho dalších procesorů velmi často krátkodobě zamyká pro čtení. Počítadlo je proto stále větší než 1 (vždy najdeme aspoň jeden procesor, který chce číst), takže uzamčení pro zápis se nikdy nepovede. Tomuto stavu se někdy říká vyhladovění.

Úkol 1: Řešení bez vyhladovění

Ukážeme trochu složitější konstrukci RW spinlocku, která vyhladověním netrpí. Kromě počítadla si pořídíme pomocný obyčejný spinlock S. Při zamykání RW pro čtení zamkneme S a hned ho zase odemkneme. Při zamykání RW pro zápis zamkneme S a neodemkneme ho dřív, než se zamčení RW podaří. Tím způsobíme, že jakmile začneme čekat na zamčení RW pro zápis, další požadavky na zamykání RW už budou čekat a k žádnému vyhladovění nedojde.

Ukážeme implementaci. Na adrese r0 bude opět uloženo počítadlo, na r0+4 spinlock. Budeme používat funkce zamkni a odemkni ze zadání. Opět použijeme standardní volací konvenci, takže si musíme dát pozor na to, že funkce, kterou voláme, může přepsat r0.

zamkni_pro_zápis_2:
  PUSH  {r0}
  ADD   r0, #4    @ adresa spinlocku
  BL    zamkni
  POP   {r0}
  @ sem vložíme zamkni_pro_zápis bez BX lr
  ADD   r0, #4
  BL    odemkni
  BX    lr

zamkni_pro_čtení_2:
  PUSH  {r0}
  ADD   r0, #4    @ adresa spinlocku
  PUSH  {r0}
  BL    zamkni
  POP   {r0}      @ opět adresa spinlocku
  BL    odemkni
  POP   {r0}      @ adresa počítadla
  @ sem vložíme zamkni_pro_čtení

Funkce pro odmykání zůstanou stejné – stačí jim počítadlo a pomocným spinlockem se vůbec nemusí zabývat.

Úkol 2: Problém se dvěma zámky

Deadlocku se zbavíme velice snadno: kdykoliv chceme zamknout více zámků, seřadíme je podle adres v paměti a zamykáme je v tomto pořadí. Odemykat už můžeme v libovolném pořadí.

Pojďme dokázat, že deadlock pak nemůže nastat. Nejprve si rozmyslíme, kdy deadlock vzniká: nějaký procesor se chystá zamknout zámek z₁; ten je ovšem zamčený jiným procesorem, který zrovna čeká na zámek z₂, takže neodemkne z₁ dřív, než získá z₂; další procesor drží z₂ a čeká na z₃; až nakonec nějaký procesor drží z_k a čeká na z₁.

Tuto situaci můžeme elegantně popsat orientovaným grafem. Jeho vrcholy budou zámky, hrana povede ze z_i do z_j, pokud nějaký procesor má zamčený zámek z_i a čeká na z_j. K deadlocku dojde právě tehdy, když v tomto grafu existuje cyklus.

Seřazením zámků podle adres jsme způsobili, že kdykoliv v grafu existuje hrana z₁z₂, leží z₁ na nižší adrese než z₂. Na jakémkoliv cyklu by tudíž musely adresy stále růst, a to není možné. Takže žádný cyklus neexistuje, tedy ani žádný deadlock.

Úkol 3: Fronta

Jak po nás zadání chtělo, frontu reprezentujeme jednosměrným spojovým seznamem (každý prvek seznamu bude v paměti tvořen jedním slovem s hodnotou a jedním s adresou následujícího prvku). Chceme umět rychle jak přidávat na konec seznamu, tak odebírat z jeho začátku. Proto si musíme pamatovat jak adresu prvního prvku (hlavičku seznamu H), tak posledního (ocásek O). Pokud hlavička, ocásek nebo následník prvku neexistují, uložíme nulovou adresu.

Kdyby byl seznam vždy aspoň dvouprvkový, úloha by byla jednoduchá. Stačilo by chránit hlavičku jedním zámkem (Z_H) a ocásek druhým (Z_O). Kdykoliv bychom chtěli přidat na konec, zamkli bychom ocáskový zámek, přidali nový prvek, nastavili adresu následníka v původním ocásku, aktualizovali adresu ocásku a odemkli zámek. Podobně odebírání z hlavičky by obnášelo pouze zamčení hlavičkového zámku.

Ještě si musíme dát pozor na to, abychom za zamčení zámku a před jeho odemčení umístili bariéru zabraňující přesunutí čtení či zápisů přes operace se zámkem. Obecně se hodí bariéry doplnit přímo do implementace zámků, abychom se o to nemuseli explicitně starat.

Ovšem pokud je seznam krátký, věci se začnou komplikovat. Hlavička a ocásek mohou ukazovat na tentýž prvek, nebo dokonce na žádný. Přidání prvku do prázdného seznamu obnáší nastavení jak hlavičky, tak ocásku. Odebrání jediného zbývajícího prvku způsobí vynulování hlavičky i ocásku. Přidání druhého prvku způsobí nastavení adresy následníka v prvním prvku, který mezitím někdo může odebírat. Zkrátka možností, co by se mohlo pokazit, je nemálo.

Proto na to půjdeme chytřeji – kdykoliv bude hrozit, že je seznam příliš krátký, zamkneme pro jistotu oba zámky (vždy nejprve hlavičkový, pak ocáskový, aby nedošlo k deadlocku). Může se nám stát, že hrozba byla nakonec planá, protože před zamčením někdo stihl do seznamu přidat další prvek. To ale nevadí – důležité je, abychom ve všech případech, kdy seznam je triviální, měli zamčeno.

Odebírání z hlavičky bude vypadat následovně: Nejprve zamkneme Z_H. Pak zkontrolujeme, jestli adresa hlavičky je nulová nebo hlavička nemá následníka – v těchto triviálních případech zamkneme i Z_O a můžeme podle potřeby manipulovat jak s hlavičkou, tak s ocáskem. Pokud naopak hlavička existuje a má následníka, můžeme si být jistí tím, že se tento stav během odebírání nezmění, protože kdokoliv další, kdo by chtěl odebírat prvky, čeká na hlavičkový zámek, a ten máme v ruce my – stačí tedy mít zamčený Z_H. Když jsme se vším hotovi, odemkneme Z_H a případně i Z_O.

Přidávání na konec provedeme takto: zamkneme Z_O. Pokud je adresa ocásku nulová, zamkneme i Z_H (přesněji řečeno odemkneme Z_O, zamkneme Z_H a pak znovu Z_O, abychom dodrželi pořadí zámků) a nastavíme hlavičku i ocásek na nově přidaný prvek. Pokud je ocásek nenulový, stačí nám Z_O, nastavíme následníka ocásku na nový prvek a pak nový prvek učiníme ocáskem. Nakonec odemkneme všechny zámky.

Při odebírání je potřeba si rozmyslet, že zatímco připojujeme nový prvek k původnímu ocásku, nemůže nám někdo původní ocásek pod rukama smazat. Dopadne to dobře: do té doby, než přepíšeme jeho adresu následníka, je tato adresa nulová, takže odebírající procesor by se pokusil získat oba zámky, čili by počkal, až my odemkneme. A jakmile adresu následníka přepíšeme, už původní ocásek nebudeme potřebovat, takže jeho smazání nevadí.

Úkol 4: Seznam počítadel

Pro práci se seznamem zavedeme následující pravidla:

Aby seznam nikdy nebyl prázdný a nemuseli jsme na první prvek ukazovat jinak než na ty ostatní, přidáme na začátek seznamu hlavičku. To je pevný prvek, jehož klíč ani počítadlo nebudeme používat.
Každý prvek bude vybaven svým zámkem. Obsah prvku (počítadlo a adresu následníka) smíme číst i zapisovat jen tehdy, když máme zamčený příslušný zámek.
Seznam procházíme vždy ve směru od začátku do konce. Zkoumáme-li prvek, máme ho zamčený a také máme zamčeného jeho předchůdce.

Procházení seznamu tedy probíhá takto: Nejprve zamkneme hlavičku. Pak z ní přečteme adresu následníka (tedy prvního opravdového prvku), zamkneme tohoto následníka a přesuneme se do něj. Obecně máme zamčený nějaký prvek x a jeho předchůdce p. Vždy přečteme z x adresu následníka n, zamkneme n a odemkneme p. Pak se n stane novým x a x novým p.

V každém okamžiku máme zaručen exkluzivní přístup k úseku seznamu mezi p a x. Díky tomu můžeme pracovat s počítadlem v x, vložit nový prvek mezi p a x, jakož i smazat x.

Jelikož všechny procesory zamykají zámky ve stejném pořadí, nemůže dojít k deadlocku.

Ještě dodejme, že bychom se také mohli pokusit místo zamykání upravovat ukazatele atomicky pomocí STREX. Takové pokusy většinou selžou na recyklování adres: pokud prvek vytažený ze seznamu vzápětí zapojíme na jiné místo, můžeme se nachytat na to, že stejná adresa prvku neimplikuje stejnou roli prvku v seznamu.

Závěrem

Jak vidíme, paralelní přístup k datovým strukturám je záležitost značně ošemetná. I v našich jednoduchých případech bylo docela obtížné rozmyslet si, že si procesory nemohou navzájem škodit a že nemůže nastat deadlock ani vyhladovění.

Proto si při praktickém paralelním programování obvykle vytvoříme knihovnu pro základní paralelní datové struktury (různé fronty, slovníky a podobně), detaily zamykání necháme schované uvnitř implementace knihovny, a zbytek programu bezpečně stavíme z hotových kostiček.

I tento přístup má své mouchy: jak jsme viděli ve 2. úkolu, i když máme jednotlivé atomické seznamy, neumíme snadno zařídit atomický přesun z jednoho seznamu do druhého. Naše řešení muselo zasáhnout dovnitř implementace seznamu a mluvit do toho, v jakém pořadí se zamyká.

Někdy se proto může hodit zacházet s pamětí abstraktněji a výpočet rozdělit do transakcí. V každé transakci si vedeme žurnál (log) všech přístupů do sdílené paměti. Kdykoliv z paměti přečteme nějakou hodnotu, zapíšeme do žurnálu, odkud jsme četli a co jsme dostali. Kdykoliv chceme zapisovat, tak to neprovedeme přímo, ale pouze zapíšeme do žurnálu, kam chceme co zapsat. (Při čtení tedy musíme také kontrolovat žurnál.)

Na konci transakce provedeme commit. Ten atomicky zkontroluje, že přečtené hodnoty ve sdílené paměti mezitím nikdo jiný nezměnil, a zapíše do sdílené paměti to, co jsme změnili my. V praxi se to může realizovat například společným zámkem pro commity transakcí. Každá transakce se tedy tváří, jako by se provedla atomicky. Musíme ovšem počítat s tím, že commit může selhat, a tím pádem je potřeba celou transakci zopakovat. Je to tedy takové zobecnění mechanismu LDREX/STREX na libovolně mnoho přístupů do paměti.