Druhá série třicátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 30-2-1: Zaneprázdněný org
- 30-2-2: Hardwarový generátor
- 30-2-3: Šíření viru podruhé
- 30-2-4: Komprimace
- 30-2-5: Autovysavač
- 30-2-6: Parlamentní metro
- 30-2-7: Paměť očima assembleru
 30-2-1 Zaneprázdněný org (Zadání)
30-2-1 Zaneprázdněný org (Zadání)
Nechť N značí počet týdnů v databázi, M počet různých hodnot zaneprázdněnosti v databázi a Q počet dotazů.
V první řadě se zbavíme nutnosti zacházet s velkými čísly – zadání totiž neslibuje, že hodnoty zaneprázdněnosti budou jakkoliv rozumné nebo malé. Ideálně bychom chtěli přečíslovat hodnoty na vstupu na čísla 1 až M, přičemž to samé přečíslování pak potřebujeme i během dotazování. Jak to zařídit, si necháme na samotný závěr řešení a pro teď si dovolíme předpokládat, že čísla už přečíslovaná jsou.
Úlohu můžeme zjednodušit použitím prefixových součtů. Nechť dH(K) značí odpověď na otázku „Kolikrát se v prvních K týdnech vyskytlo hodnocení H?“. Rozmyslete si, že odpověď na dotaz „Kolikrát se v týdnech ℓ až r vyskytlo hodnocení H?“ je rovna dH(r) - dH(l-1).
Hodnoty dH si umíme přímočaře předpočítat: vždy položíme dH(i) = dH(i - 1), a pokud Ai = H, zvětšíme ještě dH(i) o jedna. Můžeme tedy spočíst dH pro všechna H (1 ≤ H ≤ M), čímž dostáváme algoritmus potřebující O(NM) času na předvýpočet a O(1) času na dotaz.
Předvýpočet zbytečně brzdí fakt, že v naprosté většině dH se „nic neděje“: pro konkrétní i zůstanou téměř všechna dH(i) oproti dH(i - 1) stejná, jen jedno se zvýší o jedničku. Toho můžeme využít a zrychlit předvýpočet na úkor drobného zpomalení dotazů.
Pro každé H si v nějakém poli pH zapamatujeme jen ty pozice, na kterých se dH mění, tedy přesně ty pozice i, pro která Ai = H. Všechna pH zvládneme spočítat najednou tak, že projdeme A zleva a za každé políčko připíšeme do příslušného pH aktuální index. Po doběhnutí budou v každém pH indexy všech výskytů H v poli A, navíc vzestupně seřazené.

Časová i paměťová složitost předvýpočtu je Θ(N), protože vše zařídíme jedním průchodem pole a součet velikostí všech pH je N.
Jak budeme odpovídat na dotaz? Pro konkrétní H a i chceme rychle spočítat dH(i), tedy počet výskytů hodnoty H v A1,… ,Ai. Všechny výskyty máme ale zapsané v pH, a ještě seřazené. Rozmyslete si, že odpověď je přesně index, na kterém skončíme, když v pH binárně vyhledáme i. Konkrétně použijeme variantu binárního vyhledávání, která v případě, že se i v poli nenachází, najde nejbližší nižší číslo (úprava není složitá a naleznete ji i v naší kuchařce).
Pro každý dotaz tedy provedeme dvě binární vyhledávání v poli o velikosti až O(N). Časová složitost jednoho dotazu tedy bude O(log N). Paměťová zůstává O(N), protože si musíme pamatovat všechna pH.
Přečíslování
Zbývá si říct, jak budeme provádět přečíslování. Máme tu výhodu, že nám nezáleží, jaká zaneprázdněnost se přečísluje na co, dokud budou přečíslovaná čísla dostatečně malá. Můžeme tak použít velmi jednoduché řešení založené na hešování. V případě, že bychom chtěli například zachovat i vzájemnou velikost (aby bylo jedno přečíslované číslo větší než jiné právě tehdy, když tomu tak bylo i před přečíslováním), mohli bychom použít kombinaci řazení, odstranění duplikátů a následného binárního vyhledávání – detaily si zkuste rozmyslet.
V hešovacím řešení budeme vyrábět hešovací tabulku, která každé zaneprázdněnosti unikátně přiřadí číslo mezi 1 a M. Budeme pole procházet zleva a kdykoliv narazíme na zaneprázdněnost, kterou ještě nemáme v tabulce, přidáme ji a přiřadíme jí nejmenší ještě nepoužité číslo (což je, mimochodem, počet záznamů v tabulce plus jedna).
Tak v průměrném čase O(N) vyrobíme tabulku, které se v O(1) (také v průměrném čase) můžeme ptát na přečíslování libovolné hodnoty. Složitost přečíslování se tedy „ztratí“ ve složitosti předvýpočtu i dotazování, takže časová i paměťová složitost algoritmu zůstane nezměněna.
Během dotazování se nám také může stát, že danou hodnotu neumíme přečíslovat, protože ji vidíme poprvé. Pak je ale odpověď zřejmě nula.
 30-2-2 Hardwarový generátor (Zadání)
30-2-2 Hardwarový generátor (Zadání)
Protože jsou čísla hardwarovým generátorem generována rovnoměrně, je pravděpodobnost, že se trefí do intervalu [a, b], rovna b - a. Takže si můžeme pro každý prvek, který chceme generovat, vyrobit interval stejné délky, jakou má mít pravděpodobnost. Navíc intervaly vyrobíme tak, aby na sebe navazovaly a dohromady tak pokryly celou plochu [0, 1]. Pak už nám zbývá jenom umět v seznamu intervalů najít ten, který obsahuje vygenerované číslo, což můžeme udělat binárním vyhledáváním v čase O(log M). To je sice docela rychlé, ale jde to lépe.
První trik spočívá v tom, že si vyrobíme pole, kde si na i-tý prvek zapíšeme, kolikátý interval obsahuje číslo i/M, a pak ho budeme používat jako vyhledávací tabulku pro „první skok“ při hledání. Tímto skokem zmenšíme prohledávaný interval na okénko velké 1/M (od i/M do (i+1)/M). Může nám v něm ale pořád zbýt až Θ(M) malých podintervalů, takže v nejhorším případě to může pořád trvat O(log M).
V průměrném případě jsme se ale dostali na konstantu, protože dohromady je tam O(M) hranic intervalů a průměrně tak budou mít v sobě vyhledávací okénka jen O(1) hranic. Předpočítání stihneme hravě lineárně, stačí projít všechny intervaly a zároveň s tím si posouvat index vždy, když se dostaneme přes index/M.
To ale pořád není úplně optimální, mohli bychom ještě chtít, aby generování trvalo vždy konstantně dlouho. Můžeme intervaly chytře rozkouskovat a rozdělit mezi okénka tak, aby se nám nikde nenahromadily, jako když jsme to udělali naivně v zadaném pořadí. Vybudujeme si tabulku, kde v každém okénku velikosti 1/M budou maximálně dva intervaly.
Abychom toho docílili, uděláme si dvě fronty – pro intervaly kratší než 1/M a delší než 1/M. Intervaly dlouhé právě 1/M vyřešíme zvlášť; na ty nepotřebujeme frontu, můžeme si prostě pamatovat jejich počet a na konci je umístit do zbylých okének.
V každém kroku algoritmu vytáhneme z fronty krátkých intervalů jeden interval, umístíme ho na začátek okénka a doplníme částí jednoho dlouhého intervalu. Zbytek toho dlouhého vrátíme do fronty (podle jeho zbývající délky ho zařadíme do patřičné fronty).
Například pro čtyři intervaly délek 0.7, 0.1, 0.1, 0.1 bude původní a nové rozdělení vypadat následovně:

Všimneme si, že pokud budeme takto postupovat, v každém kroku zaplníme jedno okénko a celkový počet zbývajících intervalů snížíme o jedničku (krátký interval spotřebujeme, zatímco dlouhý jen zkrátíme; případně spotřebujeme jeden interval délky přesně 1/M). Tedy počet nezaplněných okének bude vždy stejný jako počet zbývajících intervalů (na začátku je obojího M a snižují se společně).
Ovšem musíme ukázat, že vždy můžeme popsaný krok udělat. Dle argumentu výše nám na začátku libovolného kroku zbývá k okének k zaplnění s celkovou délkou k/M a k intervalů k umístění. Celková délka zbývajících intervalů musí být také k/M, jinak bychom nemohli zbylá okénka přesně zaplnit. A snadno si rozmyslíte, že když máme k intervalů celkové délky k/M, buď mají všechny délku přesně 1/M, nebo je mezi nimi alespoň jeden kratší a alespoň jeden delší.
Hledání provedeme velmi podobně jako v průměrně konstantní verzi – najdeme si okénko, podíváme se, jestli je číslo v prvním nebo druhém intervalu, a podle toho vrátíme výsledek.
Operace s frontou (neprioritní) trvají O(1) a pro každé okénko a každý interval na vstupu jich uděláme konstantně mnoho. Nic dalšího překvapivého algoritmus nedělá, takže složitost vybudování vyhledávací tabulky je O(M). Složitost hledání je O(1), provede se tam jenom jedno vyhledání v tabulce a porovnání. Dokonce i prakticky by bylo o dost rychlejší než binární vyhledávání, nejsou tam žádné velké skryté konstanty.
 30-2-3 Šíření viru podruhé (Zadání)
30-2-3 Šíření viru podruhé (Zadání)
Nejprve bychom se vám měli přiznat, že tato úloha dopadla úplně jinak, než jsme plánovali. Její autor měl totiž vymyšlené řešení, které bylo elegantní, lineární … a bohužel dočista špatně. A ani dlouhé přemýšlení a pátrání v moudrých knihách ho nepomohlo zachránit. Inu, i mistr kat se někdy utne.
Přesto jsme pár zajímavých řešení vymysleli. Využívají trochu drsnější prostředky, než na jaké jsme v KSPčku zvyklí. Ale nebojte se, (moc) nekoušou.
Ještě si připomeňme úlohu: pro každý vrchol v orientovaném grafu chceme zjistit, kolik vrcholů je z něj dosažitelných (tj. vede do nich cesta). Označíme N počet vrcholů a M počet hran.
Nejprve si rozmyslíme triviální pomalé řešení: z každého vrcholu spustíme prohledávání do hloubky nebo do šířky a spočítáme, do kolika vrcholů se dostalo. Jedno prohledání trvá O(M), všechna dohromady O(NM). [Drze předpokládáme, že graf nemá izolované vrcholy, jinak bychom museli psát O(N+M) místo O(M), abychom stihli inicializaci.]
Lehčí varianta a bitové vektory
Nyní ukážeme, jak trochu rychleji vyřešit lehčí variantu. V ní máme slíbeno, ze graf neobsahuje žádné cykly. Takové grafy můžeme topologicky uspořádat – tedy očíslovat vrcholy tak, aby hrany vedly vždy z vrcholu s nižším číslem do vrcholu s vyšším číslem. Jak víme z grafové kuchařky, topologické uspořádání lze najít v čase O(M).
Nechť v1,… ,vN je nějaké topologické pořadí vrcholů. Pro každý vrchol vi budeme chtít spočítat, které vrcholy z něj jsou dosažitelné. To budeme reprezentovat polem Mi, které bude obsahovat N nul a jedniček, přičemž na j-tém místě bude 1 právě tehdy, když vj je dosažitelné z vi.
Tato pole budeme počítat v opačném topologickém pořadí. MN je snadné: jelikož z vN nemůže vést žádná hrana, je z vN dosažitelný pouze on sám; proto MN[N]=1 a všechna ostatní MN[j]=0. Spočítat ostatní Mi nebude o mnoho složitější. Představme si, že chceme spočítat Mi a už známe všechna Mj pro j>i. Tehdy se podíváme na všechny vrcholy vj, do nichž vede hrana z vi, a spočítáme logický or jejich polí Mj. Přesněji řečeno, Mi[k] nastavíme na 1 právě tehdy, existuje-li j takové, že vivj je hrana a Mj[k]=1. A nakonec nastavíme Mi[i]=1, protože každý vrchol je dosažitelný ze sebe sama.
Proč to funguje? Pokud je z vi dosažitelný vk, znamená to, že z vi do vk vede nějaká cesta. Ta je buďto triviální (tehdy i=k), nebo má nějaký druhý vrchol vj (j>i). Z něj je ovšem také dosažitelný vk, takže Mj[k]=1. Proto náš algoritmus nastaví Mi[k]=1. A opačně: kdykoliv náš algoritmus prohlásí, že z vi je dosažitelný vk, učiní tak proto, že je vk dosažitelný z nějakého vrcholu vj, do nějž z vi vede hrana.
Algoritmus je tedy správně. Jakou má časovou složitost? Pro každý vrchol počítáme or tolika polí, kolik do vrcholu vede hran. Celkem tedy zorujeme tolik polí, kolik je v celém grafu hran, tedy M. Jelikož jeden or trvá O(N), dostaneme dohromady O(NM). Ještě ale musíme pro každý vrchol spočítat, kolik je v jeho poli jedniček. To stihneme v čase O(N2), takže celý algoritmus poběží v O(NM + N2) = O(NM).
Vida, to je stejně pomalé jako triviální algoritmus. Tak si pomůžeme oblíbeným trikem: každé pole rozdělíme na bloky velikosti ⌈ log2 N⌉ a tyto bloky zakódujeme do přirozených čísel: nuly a jedničky v bloku prohlásíme za dvojkový zápis čísla. Vzniklá čísla jsou menší než R = 2⌈ log2 N⌉ ≤ 2N, tedy žádné veliké obludy, které by se nevešly do běžné číselné proměnné. A or polí pak stačí počítat po blocích: za každý blok spočítáme jenom jeden bitový or dvou čísel v konstantním čase.
Tím jsme orování bloků (log N)-krát zrychlili, takže jsme ze složitosti O(NM) udělali O(NM / log N). Nevelké zrychlení, ale aspoň nějaké. (Mimochodem, to není žádný čistě teoretický trik: bitová pole se takto v programech reprezentují běžně a vyplácí se to.)
Složitost celého algoritmu nám ovšem kazí závěrečné počítání jedniček v čase O(N2). I to můžeme zrychlit pomocí bloků: předpočítáme si tabulku c(0), …, c(R-1), která nám řekne, kolik je v každém možném kódu bloku jedniček. Tabulku si pořídíme snadno: položíme c(0)=0 a c(1)=1, pak pro všechna i vypočteme c(2i)=c(i), c(2i+1)=c(i)+1. Pomocí této tabulky pak spočítáme jedničky v poli (log N)-krát rychleji než předtím.
Vše dohromady pak potrvá O(NM / log N + N2 / log N) = O(NM / log N).
Převod těžší varianty na lehčí
Nyní vyřešíme obecnou variantu, v níž už může graf obsahovat cykly. Využijeme dalšího šikovného nástroje z naší kuchařky o grafech, totiž komponent silné souvislosti. Komponenta silné souvislosti je skupina vrcholů, ve které se dá dostat z každého do každého. Všechny tedy budou mít stejný výsledek.
Pořídíme si graf komponent silné souvislosti. To je graf, jehož vrcholy odpovídají komponentám původního grafu a hrana vede z C1 do C2 právě tehdy, když v původním grafu vede hrana z nějakého vrcholu v1∈C1 do nějakého vrcholu v2∈C2. (Také si to můžeme přestavit tak, že každou komponentu stáhneme do jediného vrcholu.)
V knížce Průvodce labyrintem algoritmů se dokazuje, že graf komponent je možné sestrojit v čase O(M) a že tento graf neobsahuje cykly. Můžeme na něj tedy spustit předchozí řešení. Z něj se dozvíme, která komponenta je dosažitelná z které. Pak stačí pro každý vrchol posčítat velikosti všech komponent, které jsou dosažitelné z jeho komponenty.
Konstrukce grafu komponent trvá O(M), předchozí řešení seběhne v čase O(NM/ log N) a závěrečné posčítání stihneme v O(N2). I pro obecný graf tedy úlohu umíme vyřešit v čase O(N2 + NM/ log N).
Ještě dodejme, že někteří z vás se pokoušeli při konstruování grafu komponent různě spojovat vrcholy a opomněli, že při takové operaci je potřeba přepojovat hrany. Právě kvůli hranám má takový algoritmus časovou složitost O(NM).
Kouzlo s násobením matic
 Pro husté grafy (což jsou ty, které mají řádově N2 hran) existuje
ještě efektivnější algoritmus založený na násobení matic. Pojďme ho
alespoň stručně načrtnout.
Pro husté grafy (což jsou ty, které mají řádově N2 hran) existuje
ještě efektivnější algoritmus založený na násobení matic. Pojďme ho
alespoň stručně načrtnout.

Vrcholy zadaného grafu očíslujeme v1,… ,vN. Vytvoříme matici sousednosti grafu, což je matice A rozměrů N×N obsahující nuly a jedničky. Na políčko Aij napíšeme jedničku právě tehdy, když z vi do vj vede hrana. Ukážeme, jak z této matice spočítat matici dosažitelnosti, která svými nulami a jedničkami indikuje, odkud kam vede cesta. Posčítáním hodnot v řádcích se z matice dosažitelnosti dozvíme řešení naší úlohy.
| N |
| k=1 |
To je skoro to, co potřebujeme, jen bychom namísto právě t hran chtěli nejvýše t – pak bychom dosadili libovolné t≥ N a nenulová čísla ve výsledné matici by řekla přesně to, mezi kterými dvojicemi vrcholů vede nějaká cesta. Snadná pomoc: nastavíme všechna Aii na jedničky. Tím jsme vlastně do grafu přidali smyčky: hrany vedoucí z vi zase do vi. Každý sled kratší než t pak můžeme procházením smyček doplnit na délku právě t. Počet sledů se změní nějak bláznivě, protože různě dlouhé sledy lze doplňovat různým počtem způsobů, ale důležité je, že nenulový počet sledů stále indikuje dosažitelnost.
Stačí tedy matici A s přidanými jedničkami (té říkejme třeba A) umocnit na aspoň N-tou. To by šlo provést N-1 násobeními matic, ale jde to i rychleji: budeme A opakovaně umocňovat na druhou, čímž získáme postupně A1, A2, A4, A8, … až po ⌈ log2 N⌉ krocích získáme At pro nějaké t≥ N. Aby nám během výpočtu nevznikala obrovská čísla, po každém násobení matic všechny nenuly přepíšeme na jedničky (tím určitě zachováme nenulovost finálního výsledku a mezivýsledky nebudou větší než N).
Náš algoritmus tedy provede O(log N) násobení matic velikosti N×N. Kdybychom matice násobili podle definice, trvalo by jedno násobení O(N3) a celý výpočet O(N3 log N), což je určitě pomalejší než triviální řešení. Můžeme ovšem využít toho, že matice lze násobit i efektivněji: například v Průvodci labyrintem algoritmů najdete Strassenův algoritmus pracující v čase O(N log2 7) ≈ O(N2.807) a existují i rychlejší. Obecně pro každý algoritmus na násobení matic v čase O(Nω) získáme algoritmus pro naši úlohu o složitosti O(Nω log N).
Pokud je M blízké N2, bude NM/ log N ≈ N3/ log N, což je asymptoticky víc než N2.807 log N. V takovém případě má maticový algoritmus lepší složitost než or-ovací.
Na závěr dodejme, že i toho logaritmu se lze chytrým trikem zbavit. Zvědavý čtenář příslušný trik najde v Medvědových skriptíčkách Krajinou grafových algoritmů v kapitole o tranzitivních uzávěrech.
 30-2-4 Komprimace (Zadání)
30-2-4 Komprimace (Zadání)
Jak dokazuje počet řešení za plný počet bodů, tato úloha není tak těžká, jak by se na první pohled mohlo zdát.
Nejprve se zbavíme nutnosti pracovat s bloky: pro každé políčko jsme schopni
hned napsat, jaký znak na něm má být (to když políčko leží v bloku typu D),
nebo odkud na něj máme znak zkopírovat (to když leží v bloku typu R). Jediné,
co k tomu potřebujeme umět, je rozhodnout, v jakém bloku políčko leží
a kolikáté v daném bloku je, což snadno zařídíme třeba tak, že už během čtení
popisů bloků postupně políčka „značkujeme“ čísly bloků.
Představme si, že do každého políčka buď napíšeme, co v něm je, nebo z něj nakreslíme šipku vedoucí do políčka, na které se odkazuje. Tím jsme vlastně dostali orientovaný graf. Když ještě ke všemu směr šipek obrátíme, dostaneme i návod, jak zjistit hodnotu v jednotlivých políčkách: budeme procházet již známá políčka (to jsou na začátku ta, do kterých nevede žádná hrana) a znaky u nich napsané kopírovat po šipkách z nich vedoucích.

Takto se dříve či později zastavíme a v tom okamžiku buď jsou všechna políčka určená, nebo data nelze určit jednoznačně. Proč? V tom okamžiku totiž z žádného určeného políčka nevede šipka do žádného neurčeného, takže hodnoty neurčených políček už nemůžeme nijak zjistit (a můžete si rozmyslet, že do libovolného z nich můžeme napsat jak nulu, tak jedničku, a v obou případech budou data konzistentní).
Algoritmus, který jsme popsali, není vůbec těžké naimplementovat. Stačí si pro
každé políčko spočítat seznam všech vrcholů, do kterých z něj máme nakopírovat
hodnotu (až ji zjistíme), což zvládneme jedním průchodem pole. Pak už provádíme
poměrně standardní proceduru postupného odtrhávání vrcholů v grafu (popsanou
například v naší grafové kuchařce, v kapitole
o topologickém uspořádání). Vrcholy,
které chceme odtrhávat, si pamatujeme ve frontě, do které na začátku přidáme
všechna již vyřešená políčka (tedy ty v blocích typu D) a v průběhu do něj
přidáváme políčka, kterým jsme právě určili hodnotu.
Existuje ještě mnohem jednodušší algoritmus, který však využívá rekurze a není tedy vhodný, pokud váš programovací jazyk například podporuje jen malé vnoření rekurzivního volání. Budeme v postatě provádět to samé, ale „zezhora“: pro každé políčko se kouzelné funkce zeptáme, jaká hodnota by na tomto políčku měla být. Kouzelná funkce buď zjistí, že na políčku nějaká hodnota je (a hned ji vrátí), nebo že do našeho políčka A se má zkopírovat hodnota z nějakého jiného políčka B. V tom případě zavolá sama sebe na políčko B a při návratu z rekurze získanou hodnotu do políčka A uloží. Poslední detail je velmi důležitý: pokud pak funkci zavoláme znovu, nebude spouštět potenciálně velmi dlouhý řetězec dalších volání, ale odpoví okamžitě.
Tato implementace má však jeden zásadní háček: pokud například políčko A
ukazuje na políčko B a B ukazuje na A, dostaneme se do nekonečné smyčky.
Tento problém má však jednoduché řešení: pokud při zpracovávání políčka A
zjistíme, že ještě nevíme jeho hodnotu a musíme se zanořit do rekurze,
poznačíme si nejprve k políčku A příznak
„rozpracováno“. Když jsme pak zavoláni na nějaké políčko a zjistíme, že už je rozpracováno,
nutně to znamená, že závislosti jsou cyklické. V takovém případě můžeme z celé
rekurze vyskočit a odpovědět NEJDE (popř. vrátit nějaký neplatný znak
a na konci celé pole projít a zkontrolovat, zda v něm nejsou nějaké neplatné
znaky).
Oba algoritmy mají paměťovou i časovou složitost O(N), kde N je délka nezkomprimovaných dat. V prvním případě pracujeme s grafem s O(N) vrcholy a O(N) hranami, v tom druhém se pro každou hodnotu rekurzíme nejvýše jednou a na další dotazy odpovídáme v konstantním čase (a celkový počet dotazů je O(N)).
Program (C) – rekurzivní funkce
Program (Python 3) – šíření grafem
 30-2-5 Autovysavač (Zadání)
30-2-5 Autovysavač (Zadání)
Úloha po nás chce najít v matici M ×N okénko velikosti P ×Q s největším mediánem. Tak bychom mohli projít všechna okénka dané velikosti, pro každé spočítat medián a určit, který z nich byl největší. Okének bude (M-P+1) ·(N-Q+1), počítejme, že je to řádově O(MN), patologické případy, kdy P i Q jsou malé, nebo naopak skoro stejně velké jako M a N, zanedbejme jako nezajímavé. V každém okénku je PQ čísel a medián lze spočítat v lineárním čase, takže celkem bude spočítání maxima trvat O(PQMN).
Možná vás zajímá, jak se počítá medián v lineárním čase – pokud by nám stačil randomizovaný algoritmus s průměrně lineární časovou složitostí, můžeme použít poměrně přímočarý algoritmus QuickSelect. Ten hledá i-tý nejmenší prvek v poli a medián je přesně ((M+1)/2)-tý nejmenší prvek. V krátkosti funguje následovně: Vybere si náhodně jeden prvek a bude mu říkat pivot. Pak rozdělí pole na dvě části: prvky menší než pivot a prvky větší než pivot. Podle velikosti částí jednoduše zjistí, do jaké z nich i-tý nejmenší prvek patří, a zavolá se rekurzivně na tuto část. Protože se v každém kroku rozdělí pole asi na polovinu, ve výsledku najití mediánu trvá lineárně dlouho. Poctivější popis a také nerandomizovaný algoritmus s lineární časovou složitostí najdete v kuchařce Rozděl a panuj.
Složitost O(PQMN), respektive O(PM) pro lehkou verzi ale není nic moc, tak se pojďme podívat na lepší řešení. Bude založené na binárním vyhledávání.
Jelikož medián každého okénka je jedním z MN čísel v matici, hledaný největší medián je také jedním z nich. Takže si všech MN čísel setřídíme a začneme binárně hledat mezi nimi. V každém kroku potřebujeme zjistit, jestli nějaké číslo x, které právě držíme v ruce, je menší než největší z mediánů. To je totéž jako otázka, zda existuje okénko, jehož medián je větší než x.
Zkusme nejprve zjistit, zda je medián jednoho konkrétního okénka větší než x. K tomu stačí spočítat, kolik je v okénku prvků větších než x. Pokud více než PQ/2, je i medián větší než x. Toto můžeme postupně provést pro všechna okénka, ale … trvalo by to O(PQ) pro jedno okénko a O(PQMN) pro všechna, takže bychom si tím vůbec nepomohli.
Ukážeme, že totéž jde spočítat v čase O(MN) pomocí dvojrozměrných prefixových součtů. Vyrobíme si pomocnou matici nul a jedniček, která bude mít jedničky právě tam, kde v původní matici byly prvky větší než x. Pro pomocnou matici spočítáme dvojrozměrné prefixové součty (viz základní kuchařka). To trvá O(MN) a pak už umíme pro každé z O(MN) okének spočítat v konstantním čase, kolik má v pomocné matici jedniček, čili kolik je v původní matici prvků větších než x.
Ve výsledku potřebujeme O(MN log MN) času na setřídění všech čísel v tabulce, abychom mohli provést binární vyhledávání. Pak O(log MN)-krát zkontrolujeme, jestli existuje nějaké okénko s mediánem aspoň x, což pokaždé trvá O(MN). Dohromady bude tedy algoritmus mít časovou složitost O(MN log MN).
 30-2-6 Parlamentní metro (Zadání)
30-2-6 Parlamentní metro (Zadání)
V první řadě se omlouváme všem, kteří kvůli nejasnosti v zadání úlohu pochopili jinak, než bylo zamýšleno. Ač se to v zadání explicitně nepíše, rychlosti průjezdů tunely mohou být libovolná reálná čísla, nejen čísla přirozená.
Úlohu lze snadno převést na grafovou: vrcholy budou stanice, hrany tunely mezi nimi, ohodnocení hran bude délka příslušných tunelů. Nejprve vyřešíme lehčí variantu, kdy je graf cesta (a start a cíl jsou na jejích krajích).
Pojďme nejdřív vyřešit ještě lehčí variantu, kdy má cesta délku dva. V celé úloze budeme dále předpokládat, že kapacita baterie je rovna jedné: pokud by kapacita byla nějaké E, můžeme nejdříve předstírat, že je rovna jedné, a pak všechny rychlosti číslem E přenásobit. Rozmyslete si, že tak z optimálního řešení dostaneme opět optimální.
Určitě se vyplatí vybít celou baterii. Prvním tunelem proto projedeme nějakou rychlostí v, 0<v<1, zatímco druhým projedeme rychlostí 1 - v. Má-li první tunel délku s1 a druhý tunel délku s2, je čas strávený v prvním tunelu roven t1 = s1 / v, čas strávený v druhém tunelu roven t2 = s2 / (1-v) a celkový čas, který chceme minimalizovat, je t = s1 / v + s2 / (1 - v).
Pokud znáte derivace, jistě umíte pomocí zderivování tohoto výrazu podle v najít jeho minimum. Vladimír Chudý však přišel na zajímavou geometrickou interpretaci: Jelikož s = v · t, můžeme si úlohu představit tak, že chceme nakreslit dva obdélníky o pevně daných obsazích s1 a s2 se stranami (volitelných) délek v a t1, resp. 1-v a t2. V tomto nakreslení chceme minimalizovat součet časů, tedy t1 + t2.
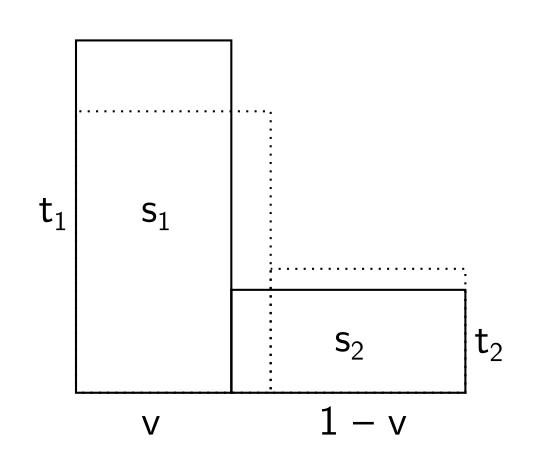
Představme si, že obdélníky nakreslíme jako na obrázku. Konkrétní rozměry obdélníků závisí jen na hodnotě v, která určuje pozici hranice mezi obdélníky. Všimneme si, že když předěl posouváme zleva doprava, první obdélník se postupně rozšiřuje, zatímco druhý se zužuje.
Určitě musí nastat situace, kdy jsou si oba obdélníky podobné (tj. „vypadají stejně“, jen jsou jinak velké). Ukážeme si, že v tomto okamžiku je součet jejich výšek nejmenší možný. Pro stručnost to ukážeme jen pro speciální případ, kdy jsou obdélníky čtverce. Důkaz pro obecné obdélníky je stejný, protože taková situace je jen vertikálně „splácnutou“/roztaženou verzí té naší.
Pro dva čtverce je součet výšek roven jedné, jelikož oba čtverce jsou stejně vysoké jako široké a součet jejich šířek je jedna. Nechť první čtverec má délku strany a, pak druhý má délku strany 1 - a. Pro spor předpokládejme, že existuje lepší řešení, tj. že pokud s hranicí pohneme na nějakou pozici v, dostaneme řešení menší než jedna. Tedy že platí s1 / v + s2 / (1 - v) < 1. Dosazením s1 = a2, s2 = (1-a)2, roznásobením výrazem v(1-v) (což je pro 0 < v < 1 vždy kladné) a posčítáním dostaneme a2 - 2av + v2 < 0, tedy (a - v)2 < 0, což nemůže nastat, protože druhá mocnina čehokoliv je nezáporná.
V optimálním řešení jsou si tedy obdélníky podobné, platí tedy v / t1 = (1 - v) / t2. Dosazením t1 = s1 / v, t2 = s2 / (1 - v) dostaneme v2 / s1 = (1 - v)2 / s2, neboli v / √s1 = (1-v) /√s2, z čehož už dokážeme v snadno spočítat (protože s1 a s2 jsou nějaké konstanty). Vyjádřeno v řeči původní úlohy, poměr rychlosti průjezdu tunelem ku odmocnině z délky tunelu je pro oba tunely stejný.
K čemu nám všechna ta námaha byla, když pořád umíme vyřešit jen případ n = 2? Výsledek o rovnosti poměrů se totiž dá zobecnit i pro delší cesty: V optimálním řešení lehké varianty platí, že pro všechny úseky je číslo vi / √si stejné. Jakto? Kdyby tvrzení neplatilo, nutně by nějaké sousední tunely i a i + 1 musely mít jiné poměry. Podíváme se na úsek cesty (vi, vi+1), jako by to byla cesta délky dva. V aktuálním řešení na ni máme z celkové kapacity baterie přiděleno vi + vi+1 energie. Když ale vi a vi+1 změníme tak, aby se poměry v / √s vyrovnaly (a přitom součet rychlostí zůstal nezměněný), určitě nezměníme množství spotřebované energie pro celou cestu a celkový čas přitom snížíme. Tím pádem jsme z údajně optimálního řešení získali „ještě optimálnější“, což samozřejmě nejde.
Máme tedy elegantní způsob, jak vyřešit lehčí variantu: Na začátku všechny délky tunelů odmocníme a pak energii tunelům rozdělíme v příslušných poměrech. Konkrétně spočteme S = √s1 + ...+ √sn a i-tému tunelu přidělíme √si / S energie.

Těžší varianta
| s1 |
| v1 |
| sk |
| vk |
| s1 |
| √s1 / S |
| sk |
| √sk / S |
Hledáme tedy cestu v grafu, pro kterou je součet nějakých hodnot na hranách co nejmenší. Na to použijeme starý dobrý Dijkstrův algoritmus. Ještě předtím však hodnoty na hranách odmocníme, protože chceme co nejmenší součet √a1 + ...+ √ak, nikoliv a1 + ...+ ak.
Časová složitost složitost je rovna O((N + M) log N), kde N je počet stanic a M počet tunelů, paměťová je O(N).
 30-2-7 Paměť očima assembleru (Zadání)
30-2-7 Paměť očima assembleru (Zadání)
Úkol 1: znaménkovost load/store instrukcí
V prvním úkolu jsme se zamýšleli, proč některé load/store instrukce mají znaménkové a bezznaménkové varianty, zatímco jiné nikoli.
První věc, kterou je třeba si uvědomit, je, že v registrech nejsou uložená čísla, nýbrž posloupnosti 32 bitů. Pokud registr obsahuje hodnotu 0xFFFFFFFE (11111111 11111111 11111111 11111110), procesor „neví“, jestli tato hodnota představuje znaménkové číslo -2, nebo bezznaménkové číslo 4 294 967 294. Je na nás a našem programu, jakým způsobem obsah registru interpretujeme. Proto i náš simulátor ukazuje u každého registru znaménkovou i bezznaménkovou interpretaci obsahu – nemůže nijak vybrat „tu správnou“.
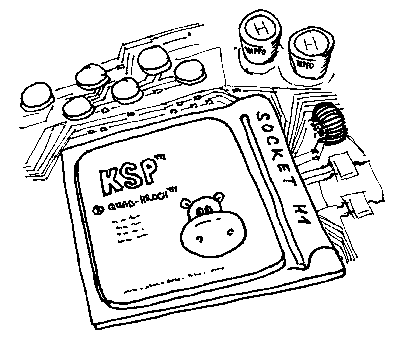
Zpět k naší otázce. Nejjednodušším případem jsou 32-bitové instrukce LDR
a STR. Ty prostě překopírují 4 bajty z/do paměti bit po bitu a je úplně
jedno, co tyto bity znamenají. Hodnota výše se do paměti uloží jako posloupnost
bajtů 0xFE, 0xFF, 0xFF, 0xFF (little endian), bez ohledu na znaménkovost.
Teď si představme, že načítáme z paměti např. 8-bitové číslo. Pokud máme v paměti bajt 0xFE, může představovat jak bezznaménkové číslo 254, tak znaménkové číslo -2. V prvním případě ho chceme do registru zapsat jako 0x000000FE, v druhém jako 0xFFFFFFFE (což je 32-bitová reprezentace čísla -2).
Vlastně řešíme následující problém: máme k dispozici např. 8-bitovou reprezentaci nějakého čísla a chceme ji prodloužit na např. 32-bitovou reprezentaci téhož čísla. Ale jak ukazuje příklad výše, toto se dělá rozdílně pro znaménková a bezznaménková čísla. V bezznaménkovém případě stačí prostě hodnotu zleva doplnit nulami.
Ve znaménkovém případě musíme provést takzvané znaménkové rozšíření. Vezmeme nejvyšší (nejlevější) bit původní reprezentace a jeho hodnotou zleva doplníme reprezentaci na požadovanou délku. A protože nejvyšší bit funguje jako znaménkový, dá se zrovna tak říct, že kladná čísla doplňujeme zleva nulami, záporná jedničkami.
Potřebujeme tedy load instrukcím říct, jaký druh rozšíření na 32 bitů mají použít: proto existují znaménkové a bezznaménkové verze.
Naopak při ukládání tohle není potřeba. Třeba pokud chceme obsah registru uložit jako 8-bitové číslo, prostě vezmeme nejnižších (nejpravějších) 8 bitů a zapíšeme je jako jeden bajt do paměti. Rozmyslete si, že tohle dá správný výsledek pro znaménková i bezznaménková čísla (pokud jsou dost malá, aby se vešla do 8 bitů).
Pro 16-bitové load/store je situace velmi analogická, jen nesmíme zapomenout, že výsledné dva bajty se uloží v pořadí little endian:
Úkol 2: obrácení pole
Postupujeme přímočaře: nejdříve prohodíme první prvek s posledním, potom druhý s předposledním atd., až skončíme uprostřed. Prohození dvou prvků provedeme tak, že je načteme do dvou registrů a potom zapíšeme na opačná místa.
Procházení pole můžeme řešit třeba tak, že si ve dvou registrech budeme udržovat adresu aktuálního levého a pravého prohazovaného prvku. Po prohození levou adresu zvětšíme a pravou zmenšíme. Skončíme, když je pravá adresa menší nebo rovna levé (narazili jsme na prostředek nebo jej překročili).
MOV r0, #0x10000
// načti délku do r1 a posuň r0 na začátek pole
LDR r1, [r0], #4
SUB r1, #1 // poslední prvek má index délka-1
ADD r1, r1, r0, lsl #4 // adresa posled. prvku
//odteď ukazují r0,r1 na pár prohazovaných prvků
smycka:
CMP r0, r1
BHS konec
// načti pár k prohození
LDR r2, [r0]
LDR r3, [r1]
// ulož opačně a posuň ukazatele
STR r3, [r0], #4
STR r2, [r1], #-4
B smycka
konec:
Úkol 3: nulování paměti
Chceme vynulovat N bajtů paměti pomocí 0.3·N + O(1) vykonaných instrukcí.
Máme k dispozici méně než jednu instrukci na bajt, takže určitě musíme jednou
instrukcí vynulovat více bajtů. Nabízí se použít instrukci STR pro nulování
bajtů po čtveřicích.
To má dva háčky. V prvé řadě N nemusí být násobkem čtyř, ale o zbylé 1–3 bajty se případně postaráme na konci, to se schová do aditivní konstanty.
MOV r1, #0x10000
MOV r2, #0
smycka:
SUBS r0, #4
STRHS r2, [r1], #4
BHI smycka
//Pokud r0 nebylo násobkem 4, v poslední iteraci
//jsme odečetli moc a dostali se do záporu
ADDLO r2, #4
// Teď mohly zbýt nejvýš tři bajty k vynulování
zbytek:
SUBS r0, #1
STRBHS r2, [r1], #1
BHI zbytek
V implementaci smyčky jsme použili několik užitečných triků. Odčítání používáme zároveň jako porovnání, čímž ušetříme jednu CMP instrukci. Díky tomu se může stát, že v poslední iteraci odečteme moc a skončíme v záporu, to ale snadno opravíme po skončení smyčky.
Existují dva obyklé způsoby, jak zapisovat smyčky. S podmínkou na začátku:
smycka:
<podmíněný skok na 'konec', pokud
se má smyčka ukončit>
<tělo smyčky>
B smycka
konec:
nebo s podmínkou na konci:
smycka:
<tělo smyčky>
<podmíněný skok na 'smycka', pokud
má smyčka pokračovat>
Smyčka s podmínkou na konci se provede vždy alespoň jednou, což se nám tady
nehodí, protože r0 může být méně než 4 a nechceme vynulovat víc paměti
než máme. Ale smyčka s podmínkou na začátku obvykle potřebuje dvě instrukce
skoku, to je hrozné plýtvání. My jsme využili toho, že na ARMu jde podmínku
připojit k libovolné instrukci a vytvořili tak hybridní smyčku s podmínkou
na začátku, která si vystačí s jednou instrukcí skoku.
| 34N + |
| O |
Trávíme více času režijí smyčky než užitečnou prací. Protože režie smyčky je
na jednu iteraci konstantní, nabízí se udělat více práce v jedné iteraci.
Třeba tak, že použijeme více instrukcí STR za sebou.

Rozmysleme si, jestli to pomůže. Pokud v těle smyčky bude k instrukcí
STR, vynulujeme na jednu iteraci 4k bajtů a provedeme k+2
instrukcí. Provedeme tedy (k+2)/4k instrukcí na vynulování jednoho bajtu.
Chceme, aby tento výraz byl nejvýše 0.3. To je jednoduchá nerovnice,
vyřešením dostáváme k ≥ 10.
Výsledný kód bude vypadat následovně:
MOV r1, #0x10000
MOV r2, #0
smycka:
SUBS r0, #40
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
STRHS r2, [r1], #4
BHI smycka
// Pokud r0 nebylo násobkem 40, v poslední
// iteraci jsme odečetli moc a dostali se
// do záporu
ADDLO r2, #40
// Teď mohlo zbýt nejvýš 39 bajtů k vynulování
zbytek:
SUBS r0, #1
STRBHS r2, [r1], #1
BHI zbytek
Tato verze pomocí 12 instrukcí vynuluje 40 bajtů, provede tedy 12/40n + O(1) = 0.3n + O(1) instrukcí, jak jsme chtěli. Použité technice se říká rozbalování smyček (loop unrolling) a běžně se používá ke zrychlení smyček s krátkým tělem. Třeba céčkové překladače takovouto úpravu dělají automaticky v rámci optimalizací.
Úkol 4: třídění
V souladu s radou v zadání budeme implementovat nerekurzivní verzi MergeSortu z třídící kuchařky. Pro jednoduchost budeme předpokládat, že délka posloupnosti je mocninou dvojky (n=2k). Algoritmus se skládá z k fází. Na začátku i-té fáze máme posloupnost tvořenou řadou bloků délky 2i-1, každý z kterýchž je už z minulých fází setříděný. V i-té fázi slijeme dvojice sousedních bloků do jednoho bloku dvojnásobné délky (2i). Na konci poslední fáze tvoří celou posloupnost jeden velký setříděný blok délky 2k, čímž máme hotovo.
Protože slévání nejde jednoduše provádět na místě, potřebujeme mít oddělený prostor pro výsledek, který nám také zadání slibuje. V kuchařce se po každé fázi obsah pomocného výstupního pole zkopíruje zpátky do původního, aby mohl posloužit jako vstup pro další fázi. To je ale zbytečné plýtvání. Místo toho stačí prostě prohodit význam těchto dvou polí. Tedy liché fáze budou používat hlavní pole jako vstup a pomocné pole jako výstup, sudé naopak.
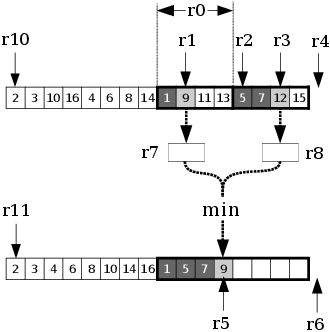
Zbývá to celé přepsat do assembleru. Možná polovinu práce tvoří rozvrhnout si, co si pamatovat ve kterém registru. Zkusme to třeba takto:
-
r0: Velikost aktuálně slévaného bloku (v bajtech, mocnina dvojky). Dva bloky velikostir0sléváme do jednoho velikosti 2·r0. -
r1: Adresa aktuálního prvku v levém zdrojovém bloku. -
r2: Adresa konce levého zdrojového bloku (ukazuje na adresu těsně za koncem, tak je obvyklé konce reprezentovat). -
r3: Adresa aktuálního prvku v pravém zdrojovém bloku. -
r4: Adresa konce pravého zdrojového bloku. -
r5: Adresa aktuálního prvku v cílovém bloku (kam se umístí příští prvek). -
r6: Adresa konce cílového bloku. -
r7,r8: Pomocné registry pro dočasné hodnoty, například prvky načtené z paměti pro porovnání. -
r9: Celková velikost pole (v bajtech). -
r10: Adresa začátku zdrojového pole (to obsahuje setříděné bloky velikostir0). -
r11: Adresa začátku cílového pole (v něm vytváříme setříděné bloky velikosti 2·r0). Na konci každé fáze prohodíme hodnoty r10 a r11.
Různá místa v poli si pamatujeme jako paměťové adresy namísto indexů, což trochu zjednodušuje přístup do paměti. Všimněte si, že si u každého bloku pamatujeme aktuální pozici a konec, ale nikoli začátek. Protože začátek ve skutečnosti k ničemu nepotřebujeme. Pro přístup do paměti nám stačí aktuální pozice, při řízení smyčky porovnáváme aktuální pozici s adresou konce.
Základní strukturu programu lze zapsat následujícím pseudokódem.
Doporučujeme současně sledovat vzorový program odkazovaný níže –
tohle je spíš návod, jak se v něm vyznat, než samostatné čtení.
Notace: = je přiřazení, neco: jsou assemblerové labely, ->
skoky (dle kontextu možná podmíněné), P: je precondition –
něco, co slibujeme, že před vstupem do tohoto místa bude platit.
r0 = 4 // slučujeme 1prvkové (4bajtové) bloky
faze:
P: r0 obsahuje velikost bloků, které chceme
v této fázi slučovat
P: bloky velikosti r0 už jsou setříděné
Nastavíme r1 a r5 na začátek prvního vstupního
a výstupního bloku.
r1 = r10
r5 = r11
blok:
// začínáme slévat dva bloky
P: r1 ukazuje na začátek levého vstup. bloku
ke zpracování, r5 na začátek příslušného
výstupního bloku
// dopočteme pravý vstup. blok a konce bloků
r2 = r1 + r0
r3 = r1 + r0
r4 = r1 + 2*r0
r6 = r5 + 2*r0
prvek:
Pokud jsme na konci levého bloku (r1==r2):
-> doberpravy
Analogicky pro pravý: -> doberlevy
P: r1 < r2, r3 < r4, r5 < r6
(v žádném bloku nejsme na konci)
Přidáme další prvek na výstup: na adresu
[r5] uložíme menší z [r1], [r3] a správně
posuneme ukazatele (viz níže)
-> prvek
doberlevy:
P: r3 == r4 // (pravý blok vyprázdněn)
Zkopíruj zbytek levého bloku (od adresy
r1 do r2 - 4) na výstup (r5 až r6 - 4)
-> konecmerge
doberpravy:
(analogicky)
konecmerge:
P: ve všech blocích jsme na konci
(r1 == r2, r3 == r4, r5 == r6)
Pokud jsme zpracovali poslední blok
(r5 >= r11+r9):
-> konecfaze
Jinak se posuneme na následující blok:
// Nový levý blok bude začínat za koncem
// aktuálního pravého.
r1 = r4
// r5 netřeba měnit, už ukazuje na
// začátek sousedního bloku
-> blok
konecfaze:
r0 = r0 * 2
prohoď r10, r11
-> faze
Jeden krok slévání (label prvek:) je jednoduchý. Načteme čísla
z aktuálních
pozic v obou vstupních blocích, porovnáme je a uložíme na výstup.
Zároveň musíme posunout výstupní ukazatel a jeden ze vstupních (podle
toho, které číslo jsme vybrali).
prvek:
// Pokud jsme v některém bloku na konci...
CMP r1, r2
BHS doberpravy // (viz vzorový program)
CMP r3, r4
BHS doberlevy
LDR r7, [r1]
LDR r8, [r3]
CMP r7, r8
// Pokud akt. prvek z levého bloku je menší,
// přidáme ho na výstup a posuneme levý pointer
STRLE r7, [r5], #4
ADDLE r1, #4
// Analogicky pro pravý
STRGT r8, [r5], #4
ADDGT r3, #4
B prvek
Zbytek programu najdete na našem webu.
Úkol 5: zatřídění do spojového seznamu
Na adrese 0x100000 je uložen pointer na začátek seznamu, v r0 pointer na nově přidávaný prvek. Předpokládáme, že struktura pro jeden prvek obsahuje 32-bitovou hodnotu a 32-bitový ukazatel na následníka.
Úkol je celkem jednoduchý, jen je třeba rozmyslet si několik okrajových případů:
- Zatřiďujeme na začátek seznamu (pak je třeba přepsat ukazatel na začátek).
- Zatřiďujeme na konec seznamu (je třeba dát si pozor, ať nezkoušíme dereferencovat null pointer).
- Seznam je prázdný (ukazatel na začátek je null).
Opět si rozvrhneme registry:
- r0 – adresa vkládaného prvku
- r1 – hodnota vkládaného prvku
- r2 – adresa aktuálního prvku seznamu, se kterým porovnáváme
- r3 – hodnota tohoto prvku
- r4 – adresa prvku předcházejícího r2
- r10 – konstanta 0x100000 (adresa pointeru na první prvek)
Samotný kód už je potom velmi přímočarý a asi nepotřebuje další vysvětlení:
LDR r1, [r0]
MOV r10, #0x100000
LDR r2, [r10]
MOV r4, #0
smycka:
CMP r2, #0
BEQ vloz
LDR r3, [r2]
CMP r1, r3
BLE vloz
MOV r4, r2
LDR r2, [r2, #4] // r2 = [r2].dalsi
B smycka
vloz:
// Vlož nový prvek mezi prvky na adr. r4 a r2
// Pokud vkládáme na začátek seznamu, r4 == 0.
// Pokud vkládáme na konec seznamu, r2 == 0.
STR r2, [r0, #4] // [r0].dalsi
CMP r4, #0
STREQ r0, [r10] // r0 je nový první prvek
STRNE r0, [r4, #4] // [r4].dalsi = r0