Druhá série třicátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 33-2-1: Ostrovní království
- 33-2-2: Hasičské stanice
- 33-2-3: Bludiště s turrety
- 33-2-4: Oprava satelitů
- 33-2-S: Šumy
- 33-2-X1: Závody formulí
 33-2-1 Ostrovní království (Zadání)
33-2-1 Ostrovní království (Zadání)
Začněme tím, co je to vůbec strom. Strom lze třeba definovat tak, že je to souvislý graf, ve kterém se nevyskytuje cyklus. Z tohoto se dá vyvodit vlastnost, že strom o n vrcholech bude mít n-1 hran. Správnost tvrzení lze nahlédnout třeba tím, že když budeme postupně odtrhávat listy, tak po n-1 odtržených listech nám bude zbývat jeden vrchol, který nebude mít hranu.
Pokud stromy neznáte, tak vám doporučujeme nahlédnout do naší základní kuchařky.
Nyní již k řešení samotné úlohy. Nejdřív předpokládejme, že pokud známe počet měst (vrcholů) a cest (hran), tak řešení je již triviální zjistit. Bude to rozdíl těchto dvou hodnot. Proč? Každý ostrov má síť cest ve tvaru stromu, a víme, že rozdíl měst a cest v jednom stromě je roven jedné. Každý ostrov tak zvětší celkový rozdíl měst a cest o hodnotu jedna.
Teď nastává ta těžší část, jak zjistíme počet měst a cest? Začneme tím, že zjistíme počet měst pomocí druhého dotazu (jestli mezi městy existuje cesta). Stačí nám najít největší index města (města jsou číslována sekvenčně). Kdybychom znali vrchní odhad na počet měst, tak bychom mohli udělat obyčejné binární vyhledávání, ale ten bohužel neznáme.
Ukážeme trik, kterým lze nalézt počet měst na log(n) dotazů, kde n je počet měst. Začněme s rozmezím měst od 0 do 1. Zeptáme se, jestli mezi městy existuje cesta, ale zároveň tento dotaz nám říká, že vůbec města existují! Pokud města existují, tak zvětšíme počet uvažovaných měst na dvojnásobek. Tedy rozmezí měst bude od 0 do 2. Obecně toto rozmezí bude od 0 do 2i. Takto budeme opakovat dokud v odpovědi bude, že města existují. Po odpovědi, že město 2i neexistuje, tak víme, že počet měst je mezi 2i-1 a 2i.
Abychom byli úplně korektní, tak rozmezí bude od 2i-1 do 2i - 1, protože určitě víme, že město 2i neexistuje. Nicméně mínus jedničku můžeme vynechat, protože na asymptotický počet dotazů konstanta nemá vliv.
Nyní najdeme počet měst pomocí binárního vyhledávání od 2i-1 do 2i. Poté stačí najít počet cest binárním vyhledáváním od 0 do n a máme vyhráno.
Kolik dotazů celkem položíme? Označme si číslem n počet měst. Při hledání prvního čísla města, které neexistuje, jsme počet měst „přestřelili“ maximálně o hodnotu n a udělali jsme přitom O(log n) dotazů (vždy jsme zvětšovali na dvojnásobek). Obě binární vyhledávání pak zabrala také maximálně O(log n) dotazů, takže celkový počet dotazů na královské ministerstvo bude O(log n).
 33-2-2 Hasičské stanice (Zadání)
33-2-2 Hasičské stanice (Zadání)
Nejprve si povšimněme, že nemá smysl, aby byl řádek a současně sloupec, ve kterém není umístěná stanice. Evidentně totiž můžeme umístit stanice do všech budov, které leží v průsečíku neobsazených řádků a neobsazených sloupců. Tyto budovy totiž nebyly dostupné z ani jedné stanice, tedy když z nich uděláme stanice, tak nepřijdeme o žádné obyvatele. Takto upravené řešení tedy zaručeně nebude horší než původní a po úpravě již nemůže existovat řádek a současně sloupec, kde by nebyla stanice.
Z předchozího odstavce tedy plyne, že má smysl se zaobírat pouze rozestavěními, kde buď v každém řádku je alespoň jedna stanice nebo v každém sloupci je alespoň jedna stanice. O ostatních rozestavěních jsme ukázali, že nemůžou být lepší než některé z uvažovaných.
Dále se zamyslíme nad případem, kdy v každém řádku bude alespoň jedna stanice. Druhý případ vyřešíme pouze prohozením řádků a sloupců.
Každá z budov musí být dostupná alespoň jednou stanicí, protože na daném řádku musí být alespoň jedna stanice. Z toho plyne, že obyvatelé mohou bydlet všude kromě hasičských stanic. Nemá tedy smysl, aby v jednom řádku bylo více než jedna stanice. Když totiž odstraníme z daného řádku všechny stanice až na jednu, tak pořád budou všechny budovy dostupné a navíc uvolníme některé stanice k bydlení. V každém řádku je tedy potřeba vybrat právě jednu budovu, kam umístíme stanici.
Snadno nahlédneme, že aby v daném řádku mohlo bydlet co nejvíce lidí, je nejlepší vybrat budovu s nejmenším počtem obyvatel.
Maximální hodnotu varianty, kdy je v každém řádku alespoň jedna stanice, tedy spočítáme jako součet všech budov bez součtu minim v každém řádku. Pro variantu, kdy je v každém sloupci alespoň jedna stanice, můžeme využit podobného algoritmu. Její hodnota tedy bude součet všech budov bez součtu minim v každém sloupci. O ostatních variantách jsme ukázali, že nemůžou být lepší. Finální výsledek tedy určíme jako maximum z předcházejících čísel.
Časová složitost je O(N·M), protože musíme projít celý vstup.
V případě, že vstup budeme zpracovávat již při průchodu, paměťová složitost může být O(M). Budeme si počítat celkový součet všech budov a současně do dvou polí pro každý řádek a sloupec minimum v něm.
 33-2-3 Bludiště s turrety (Zadání)
33-2-3 Bludiště s turrety (Zadání)
Nebýt problémů s turrety střílejícími rakety, tak by tato úloha byla vlastně velmi jednoduchá. Máme bludiště se startovní a cílovou pozicí a políčka, na která můžeme vstoupit. Nejkratší cestu bychom nalezli prohledáním do šířky ze startu, jednoduchý algoritmus s použitím jedné fronty. Možná by nás chviličku potrápilo vypsání cesty potom, co se dostaneme do cíle. Ale i to bychom vyřešili tím, že bychom si na každé políčko jednoduše napsali, odkud jsme na něj přišli. Taková pěkná jednoduchá úloha… ale ouha, on tam doktor Zloun přidal turrety.
Tak co jen cestou kontrolovat, jestli náhodou nevrazíme do rakety? Během prohledávání do šířky si můžeme držet počet kroků, které jsme udělali od startu a s každým krokem bychom kontrolovali, jestli na daném políčku není raketa. Ale nám se někdy může vyplatit počkat (jako například v ukázkovém vstupu v zadání), nebo dokonce na jedno políčko vstoupit vícekrát (například když půjdeme proti turretu střílejícím skrz dlouhý tunel, který má co pár políček „odpočívadlo“, na které uhneme a počkáme, než raketa proletí, a pak se vrátíme do tunelu). Na takové případy je obyčejné prohledávání do šířky málo.
Stav políčka se totiž bude lišit v závislosti na tom, v jakou chvíli se na něj díváme. V čase t přes něj může prolétat raketa, ale v čase t+2 už bude volně průchozí. V podstatě bychom si mohli pro každý čas t nakreslit mapu bludiště se zakreslenými pozicemi raket. S každým krokem (nebo stáním na místě) se pak posuneme na odpovídající políčko v mapě t+1.
Tím jsme si vyrobili stavový prostor, který již můžeme zase prohledávat pomocí prohledávání do šířky – jenom naše políčka budou mít tři souřadnice a to řádek, sloupec a čas. Ale ještě není vyhráno, takový stavový prostor může být obrovský (protože průchod bludištěm může klidně trvat i více sekund, než je počet políček bludiště). Takový stavový prostor by bylo obtížné držet si v paměti.
Už na příkladu v zadání si ale můžeme všimnout, že se mapy bludiště po čase opakují. Například pokud by v bludišti byly jen turrety s intervalem 3, tak máme jen tři různé mapy. Pokud bychom měli dva typy turretů s intervaly 2 a 3, tak se stejné situace budou opakovat každé šesté kolo. A v obecnosti lze říci, že pro nějakou množinu turretů se budou situace opakovat po nejmenším společném násobku jejich intervalů. V zadání jsme slíbili, že turrety budou mít rozsah intervalů jen mezi čísly 1 až 6 včetně, což dává nejmenší společný násobek 60, což je pořád ještě rozumná hodnota.
Po načtení vstupu nám tak stačí spočítat si nejmenší společný násobek všech vyskytujících se intervalů, zduplikovat si mapu v tomto počtu a pro každý turret zakreslit políčka s raketou ve správné časy (pro políčko ve vzdálenosti d od turretu s intervalem k platí, že se na něm bude raketa nacházet v časech d, d+k, d+2k, … a tak dále, dokud nepřekročíme nejmenší společný násobek). Důležité je také nezapomenout na „ohnivý ocas“ rakety (ten jsme zavedli, aby nebylo validní běžet proti raketě a tím se jí vyhnout), který je opožděný o jedno políčko za samotnou raketou.
Na každé políčko s raketou si také poznamenáme, kdy poprvé přes toto políčko raketa přelétne. Díky tomu můžeme na začátku výpočtu vstoupit i na políčka, kde by sice raketa později byla, ale ta první tam ještě nestihla dolétnout. Měli jsme v úmyslu tuto vlastnost na některých vstupech testovat, ale nakonec jsme naše zákeřné plány neuskutečnili. V ukázkovém kódu se ale můžete podívat na to, jakým způsobem se taková podmínka dá implementovat.
Pak již máme připravený kompletní stavový prostor, na kterém již můžeme spustit prohledávání do šířky. Pokud si nejmenší společný násobek intervalů turretů označíme jako K, tak každý krok z mapy t povede na mapu (t + 1) mod K. Zpětnou rekonstrukci cesty pak uděláme klasicky přes zpětné odkazy.
Časová a paměťová složitost prohledávání do šířky je lineární k velikosti stavového prostoru. Ten bude odpovídat O(KN) (kde N je počet políček), takže celková časová i paměťová složitost budou také O(KN).
 33-2-4 Oprava satelitů (Zadání)
33-2-4 Oprava satelitů (Zadání)
Řešení využívající čtyři značky je vcelku přímočaré. Na začátku každé K-tice satelitů položíme značku S, abychom věděli, kde začíná. Poté přepojíme K následujících satelitů tak, aby ukazovali opačným směrem. Nakonec správně zapojíme začátek a konec K-tice a celé opakujeme N/K-krát (počet skupin):
N, K = map(int, input().split())
p = lambda *x: print(*x, sep="\n")
p("P S")
for _ in range(n // k):
# ..-> o] -> [o -> o -> ...
# S
p("P A", "D", "P B", "T S")
# ..-> o] -> [o -> o -> ...
# S B
# A
for _ in range(K):
# ... <- o o -> o -> ...
# C A B
p("P C", "T B", "P A", "D", "P B",
"T A", "N C")
# ... <- o <- o o -> ...
# C A B
# ..-> o] <> [o <- o <- o] [o ->
# S C N
p("T S", "D", "N B", "P C", "T S", "N A",
"T C", "P S")
# .------------.
# ..-> o] [o <- o <- o] '> [o ->
# | S ^
# '----------------'
Instrukční složitost je lineární, protože se jedná o vnořené smyčky, kde vnější se opakuje N / K-krát a vnitřní K-krát, dohromady tedy O(N/K ·K) = O(N).
Tři značky
Při řešení úlohy pouze se třemi značkami musíme být opatrnější. Na otáčení směru satelitu tři značky potřebujeme (když nemůžeme ze satelitů vytvářet cyklus, v takovém případě by to šlo), proto potřebujeme na začátku otáčení každé K-tice dělat trochu více práce.
Přepojení začátku a konce K-tice, které jsme v řešení se čtyřmi značkami dělali až po jejím otočení, tentokrát uděláme předem. Díky tomu po dokončení otáčení (které uděláme úplně stejně jako při řešení 4 značek) už nebude potřeba nic dalšího dělat. Tento postup opakujeme K/N-krát (počet skupin):
N, K = map(int, input().split())
p = lambda *x: print(*x, sep="\n")
p("P A")
for _ in range(N // K):
# ..-> o] -> [o -> o -> ... -> o] -> [o ->
# A
p("D", "P B", *["D"] * (K - 1), "P C")
# ..-> o] -> [o -> o -> ... -> o] -> [o ->
# A B C
p("T A", "N C", "T C", "D", "P A")
# ..-> o] [o -> o -> ... -> o] -> [o ->
# | B C A
# '-----------------------^
p("T B", "D", "P C", "T B", "N A")
# .-----------------------v
# ..-> o] [o o -> ... -> o] -> [o ->
# | B C ^ A
# '-----------------------'
p("T C", *["D"] * (K - 2), "N B")
# .-----------------------.
# | .-------------. v
# ..-> o] [o <' o -> ... -> o] [o ->
# | B C ^ A
# '-----------------------'
p("T C", *["D", "P A", "T C", "N B", "P B",
"T A", "P C"] * (K - 1))
# .-----------------------v
# ..-> o] [o <- o <- ... <- o] [o ->
# | A B C
# '-----------------------'
Instrukční složitost je opět lineární, ze stejného důvodu jako při řešení se čtyřmi značkami.
 33-2-X1 Závody formulí (Zadání)
33-2-X1 Závody formulí (Zadání)
Předehra: Každá funkce má svůj obvod
Začneme jednoduchým pozorováním: Mějme nějakou funkci f(x1,… ,xk), která každé k-tici bitů přiřazuje jednobitový výsledek. Všimneme si, že tuto funkci jde spočítat formulí, a tím pádem i obvodem.
Proč tomu tak je? Funkci můžeme popsat tabulkou, která každé z 2k možných vstupních k-tic přiřadí výsledek. Pro xor vypadá takto:
| x1 | x2 | f(x1,x2) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Kdyby pravý sloupec obsahoval samé nuly, stačila by konstantně nulová formule (třeba x1∧ ¬x1). Pokud v něm bude právě jedna jednička, postačí and proměnných a jejich negací: například jedničce v řádku x1=x2=1 odpovídá x1∧ x2, jedničce pro x1=0, x2=1 odpovídá ¬x1∧ x2 atd. A pokud je na pravé straně jedniček více, stačí uvážit or formulí generujících jednotlivé jedničky. Pro xor tedy vyjde (¬x1∧ x2) ∨ (x1∧ ¬x2), což už vlastně známe ze zadání.
Tím pádem umíme vytvořit obvod pro libovolnou funkci. Neslibujeme, že onen obvod je malý :) Nicméně funguje a jeho velikost je pro konkrétní funkci konstantní.
Centroidy stromů
Ještě chvíli strpení, prosím. Potřebujeme vybudovat jeden užitečný nástroj pro práci se stromy. Popisujeme ho zvlášť, protože se hodí i v jiných úlohách.
Mějme nějaký strom T o n vrcholech. Centroid říkáme libovolnému vrcholu, jehož odebráním strom rozebereme na komponenty, z nichž každá má nejvýše n/2 vrcholů. V těchto komponentách můžeme zase najít centroidy a tak dále, čímž vytvoříme hierarchii čím dál menších stromečků. Jelikož počet vrcholů se pokaždé zmenší aspoň dvakrát, po maximálně log n krocích musíme dostat stromečky konstantní velikosti. (Logaritmem bez uvedeného základu myslíme vždy dvojkový.)
Zbývá dokázat, že v každém stromu existuje aspoň jeden centroid. Strom libovolně zakořeníme a pro každý vrchol v označíme p(v) počet jeho potomků (včetně v samotného). Pak najdeme nejhlubší vrchol u, pro nějž je p(u) > n/2. Dokážeme, že u je centroid. Podstromy ležící pod u mají nejvýše n/2 vrcholů (jinak by p(u) nebyl nejhlubší takový vrchol), zbytek stromu má n - p(u) < n/2 vrcholů.
Náš důkaz dokonce dává lineární algoritmus pro nalezení centroidu pomocí DFS. A když ho budeme volat rekurzivně, sestrojíme celou dekompozici v čase O(n log n). Neví se, zda to jde rychleji.
Řešení pomocí centroidů
Teď centroidovou dekompozici použijeme k vyřešení úlohy. Představme si stromovou strukturu formule – už v zadání jsme ukazovali, že tento strom odpovídá nějakému obvodu, který formuli spočítá, byť neefektivně. Označme n počet vrcholů stromu, což je asymptoticky totéž jako délka formule.
Najdeme centroid stromu. To je nějaké hradlo. Pod ním jsou nejvýše dva „dolní“ podstromy, které počítají vstupy pro naše hradlo. Hradlo pak svůj výstup předá „hornímu“ podstromu, který vydá konečný výsledek.
Situaci sledujme na následujícím obrázku: v je centroid, H horní podstrom, D1 a D2 dolní podstromy. Každý podstrom se navíc může odkazovat na vstupní proměnné formule.
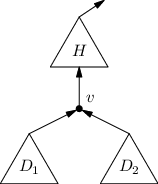
Kdyby horní podstrom byl prázdný, bylo by řešení triviální. Paralelně bychom spočítali oba dolní podstromy (ty závisí jen na vstupních proměnných formule). A pak bychom použili naše hradlo. Za jednu úroveň dekompozice bychom tedy přidali jediný takt výpočtu. Úrovní dekompozice je log n, takže obvod počítá log n taktů.
Jenže horní podstrom obvykle prázdný nebude a musí počkat na výstup našeho hradla. Mohli bychom nejdřív paralelně spočítat oba dolní podstromy, pak naše hradlo, a nakonec horní podstrom. V nejhorším případě bychom tedy za každou úroveň dekompozice počet taktů cca zdvojnásobili. Z toho by vyšel lineární počet taktů, protože bychom vlastně počítali původní strom.
Použijeme proto trik: horní podstrom spočítáme ve dvou verzích: jednu pro nulový výsledek našeho hradla, druhou pro jedničkový. To můžeme udělat předem a až budeme znát výsledek hradla, dodatečně si z verzí vybereme tu správnou.
Potřebujeme tedy sestrojit „výhybku“ – obvod, který dostane výsledek našeho hradla y a výsledky h0 a h1 obou verzí horního stromu. Jeho výsledkem pak bude hy. Výhybka je nějaká booleovská funkce tří proměnných, takže podle předehry existuje obvod, který ji počítá.
Celé to bude vypadat takto:
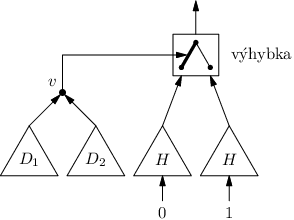
Konstrukci obvodu tedy můžeme popsat rekurzivně. Strom formule rozdělíme centroidem na dva dolní podstromy a jeden horní. Rekurzivně sestrojíme obvody pro oba dolní podstromy a pro obě možné verze horního podstromu. Výstupy těchto obvodů pak propojíme konstantně mnoha novými hradly (původní centroidové hradlo a výhybka).
Jelikož s každým krokem rekurze se velikost podstromů vydělí aspoň dvěma, hloubka rekurze činí nejvýše log n. Každá úroveň rekurze k délce výpočtu vytvořeného obvodu přispěje konstantním počtem taktů. Obvod tedy pracuje v O(log n) taktech.
Trochu pracnější bude odhadnout, z kolika hradel se vytvořený obvod skládá. Uvažujme strom rekurze našeho algoritmu – pozor, to je úplně jiný strom než ten popisující formuli! Strom má výšku v≤ log n, v každém vrcholu bydlí nějaký podproblém, při jehož řešení vznikne konstantní počet hradel. Počet hradel je tedy O(počet vrcholů stromu rekurze), což je O(počet listů stromu rekurze), jelikož každý vnitřní vrchol má aspoň 2 syny. Proto nám stačí spočítat listy.
Nechť Si značí součet velikostí všech podproblémů na i-té hladině stromu rekurze. V kořeni je zjevně S0=n. Dokážeme, že Si+1 ≤ (3/2)·Si. Mějme nějaký podproblém na i-té hladině. Označme t jeho velikost. Centroid rozdělí podproblém na dolní stromy velikostí d1 a d2 a horní strom velikosti h. Z vlastností centroidu víme, že d1, d2, h ≤ t/2 a d1 + d2 + h < t. Na (i+1)-ní hladině jsme vytvořili podproblémy velikostí d1, d2, h a ještě jednou h. Jejich celková velikost tedy je d1 + d2 + 2h ≤ t + h ≤ 3/2·t. Sečtením přes všechny podproblémy na hladině dostaneme Si-1 ≤ (3/2)·Si.
Na poslední hladině (té s listy, tedy v-té) tudíž máme Sv ≤ n·(3/2) log n. A jelikož každý podproblém v listu je konstantně velký, musí být celkový počet listů, a tím pádem i všech hradel O(n·(3/2) log n) = O(n·3 log n / 2 log n) = O(n·3 log n / n) = O(3 log n) = O((2 log 3) log n) = O(2 log 3· log n) = O((2 log n) log 3) = O(n log 3) ≈ O(n1.59). (Zde trochu švindlujeme – všechny listy nemusí ležet na poslední hladině. Ale pokud jsou některé výše, uvedené nerovnosti platí tím spíš.)
Kdyby nás ještě zajímala časová složitost algoritmu, kterým jsme obvod vytvořili, můžeme ji spočítat podobnou úvahou. V každém podproblému strávíme čas lineární ve velikosti podproblému hledáním centroidu a předáváním vstupů do rekurze. Celkový čas tedy bude lineární v součtu velikostí hladin ∑i Si. Jelikož Si rostou exponenciálně, sčítáme geometrickou řadu a její součet je asymptoticky roven nejvyššímu členu Sv. Časová složitost je tedy také O(n log 3).
Řešení pomocí heavy-light dekompozice
Takhle zajímavou úlohu přeci nemůžeme odbýt jediným řešením :) Ukážeme si proto další možný přístup. Z něj také nakonec vyjdou logaritmicky hluboké obvody, které budou navíc jen lineárně velké.
Nadále budeme používat následující značení hradel:

Nejprve si uvědomíme, že všechna uvažovaná hradla lze sestrojit pomocí jediného druhu hradel – noru. To je hradlo, které vznikne zřetězením negace za or. Vrací tedy pravdu pouze v případě, že oba jeho vstupy jsou nepravdivé.

Všimneme si, že těmito náhradami se počet hradel zvýší jen konstantně krát. Navíc se nikde nerozděluje signál. Vznikne nám tedy binární zakořeněný strom. Jeho listy jsou buď vstupu nebo konstanty a vnitřní vrcholy jsou nory.
Na něm si uděláme heavy-light dekompozici. Pokud ji neznáte, podívejte se na řešení úlohy 29-4-7. Pak se každou cestičku z těžkých hran pokusíme nahradit tak, aby se celková hloubka stromu snížila.
V původním stavu je každá cestička posloupností norů. Na každý z nich (kromě posledního) je přiveden jeden signál, muže to být i konstanta:
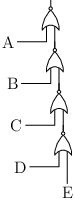
Dále si povšimneme, že záleží pouze na poloze prvního vstupu (počítáno od kořene), který má hodnotu 1. Nor, který má jako jeden vstup 1, totiž vždy vrátí nulu. Nezáleží tedy na tom, jaká hodnota přijde z druhého vstupu, z cestičky těžkých hran.
Od tohoto hradla směrem ke kořeni už jsou jen nory s jedním nulovým vstupem (za předpokladu, že jsem pracovali s nejbližší jedničkou). Ty se chovají pouze jako negace. Tedy když nad prvním hradlem se vstupem 1 je sudý počet norů, tak je celkový výstup z této části obvodu 0, v opačném případě 1.
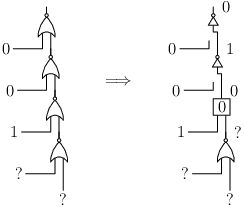
Pro každý vstup je tedy jasně dané, jaký bude výsledek, když se jedná o první vstup s hodnotou 1.
V případě, že všechny vstupy budou 0, tak je výsledek 1 právě tehdy když je počet hradel lichý.
Sestrojíme si binární stromeček, kterým nahradíme uvažovanou cestu z těžkých hran. Jeho listy budou vstupy dané části obvodu seřazené podle vzdálenosti od kořene.
Hrany v daném stromu ve skutečnosti budou dva signály. První říká, jestli v daném podstromu existuje vstup s hodnotou 1 (označme X). Pokud ano, tak druhý (označme Y) určuje, jaký by byl výstup z našeho obvodu v případě, že by daný podstrom obsahoval první jedničku.
Vnitřní vrcholy budou jen tyto dvojice signálů spojovat. Složku X spočítáme jednoduše jako or vstupních X.
Složku Y spočítáme takto: V případě, že první podstrom obsahuje jedničkový vstup, tak se použije hodnota z něho, v opačném případě se použije hodnota z druhého podstromu. V případě, že ani v jednom z podstromů není jednička, tak nás nezajímá návratová hodnota Y.
Evidentně toto jsou jen dvě logické funkce a ty dle úvodního pozorování umíme sestrojit. Pro zajímavost si ale můžeme ukázat konkrétní obvod:

Z listu povede jako existence jedničky v podstromu původní vstup a výsledek v případě první jedničky bude konstanta.
Abychom ošetřili případ, kdy všechny vstupy jsou nulové, tak na konec přidáme ještě jeden list. Ten bude vždy aktivní a jeho výsledek bude konstanta dle parity počtu norů v cestičce. Celé to bude vypadat takto:

Každou těžkou cestu jsme tedy nahradili obvodem hloubky O(log n). Z vlastností heavy-light dekompozice víme, že každá cesta z kořene do listu obsahuje O(log n) lehkých hran, mezi kterými jsou kusy těžkých cest. Celý obvod má proto hloubku O(log 2 n).
Co se prostoru týče, každý vrchol stromu jsme nahradili O(1) hradly, takže sestrojený obvod má O(n) hradel.
Další optimalizace
Předchozí algoritmus fungoval tak, že vytvořil vyvážené stromy a zavěsil je pod sebe. Ovšem pod každý strom věšíme různě velké stromy, takže výsledný obvod už může vyjít nevyvážený, a tudíž má hloubku O(log 2 n) místo O(log n).
Pojďme vymyslet, jak obvod vyvážit. Bude to fungovat tak, že velké části obvodu zasuneme do stromečku, pod kterým jsou pověšené.
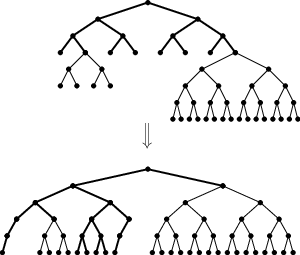
Vyvažovat budeme od listů obvodu. Tedy když budeme věšet podobvody pod nějaký stromeček, tyto podobvody už budou vyvážené.
Vyvažování stromečku bude probíhat následovně: Nejprve si vytvoříme posloupnost listů a pak nad ní vybudujeme samotný strom. (Všimněte si, že operace kombinující X a Y je asociativní, takže výsledek nezávisí na tvaru stromu, pouze na pořadí listů.)
Pro každý podobvod, který chceme pod aktuální stromeček zavěsit (ve správném pořadí), si v posloupnosti zabereme 2h políček, kde h značí hloubku podobvodu. Navíc budeme chtít, aby zabraný úsek začínal na indexu, který je násobkem 2h. Proto před něj ještě přidáme nějaký počet prázdných políček, nejvýše však 2h-1.
Na konec posloupnosti listů doplníme prázdné místo tak, aby délka posloupnosti (označme S) byla mocninou dvojky. Tím ji nejvýše dvakrát prodloužíme.

Každému podobvodu na pověšení jsem tedy přiřadili interval po sobě jdoucích listů. Ovšem díky tomu, že první z nich je na kulatém indexu 2h, podstrom jejich nejbližšího předka obsahuje pouze tyto listy.
Vytvoříme si tedy strom s počtem vrcholů odpovídajícím délce posloupnosti. Každý obvod, který chceme pověsit, pak připojíme místo podstromu pod nejbližším předchůdcem příslušného intervalu listů.
Při implementaci pak samozřejmě nemusíme vytvářet pole listů. Stačí si jen počítat indexy. Nakonec přeskočíme všechny vrcholy, které mají jen jednoho potomka (nepočítáme-li podstromy obsahující pouze přeskočené listy).
Celý výsledek tedy bude mít hloubku log S.
Takto postupně vyvážíme každý stromeček.
Odhad hloubky řešení. Nahlédneme, že délka posloupnosti při vyvažování stromečku je nejvýše čtyřikrát větší než součet délek intervalů vrcholů, které pod něj věšíme. Mezery před úseky přidají maximálně jednou tolik a doplnění na mocninu dvojky pak přidá ještě maximálně jednou tolik.
Označme celkový počet listů původního obvodu norů jako N. Z heavy-light dekompozice víme, že každý list projde jen nejvýše log N spojeními. Což ovšem znamená, že součet délek původních posloupností (tedy N) se nejvýše (log N)-krát vynásobí čtyřmi. Finální délka posloupnosti proto bude nejvýše N ·4 log N = N3. Z toho vyjde hloubka obvodu O(log N3) = O(log N).
Počet hradel v řešení je O(n). Náš strom v každém vrcholu obsahuje pouze konstantní počet hradel. Jelikož počet listů je O(n) a každý vnitřní vrchol obsahuje dva potomky, celkový počet vrcholů je O(n). Heavy-light dekompozice běží v čase O(n). Každou těžkou cestu zpracujeme v čase lineárním s její délkou, celkem tedy také O(n). Celý algoritmus proto běží v čase O(n) a spotřebuje O(n) prostoru.
 33-2-S Šumy (Zadání)
33-2-S Šumy (Zadání)
Odkazy na referenční implementace úkolů ze všech dílů seriálu naleznete v řešení posledního dílu seriálu.