Druhá série třicátého třetího ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám podzimní vydání KSP-H aneb druhé série hlavní kategorie 33. ročníku KSP.

Podobně jako v první tak i v této sérii naleznete 4 normální úlohy, bonusovou úlohu a pak také pokračování seriálu o počítačové grafice. Všechny díly seriálu můžete odevzdávat v průběhu celého roku, takže vůbec nevadí, že jste třeba první díl nestihli. Detaily naleznete u zadání seriálu. Připomínáme, že oproti loňskému ročníku se do výsledkové listiny započítávají všechny úlohy a body se již nepřepočítávají podle počtu vyřešených sérií.

Odměny & na Matfyz bez přijímaček

Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (této kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, placku a možná i další překvapení.

Zadání úloh

Letos nebudou mít úlohy žádný velký spojující příběh, na který jste mohli být zvyklí z minulých let. Namísto toho budou mít jednotlivé úlohy své vlastní malé příběhy. Snad se vám budou líbit :)

Teoretická úloha33-2-1 Ostrovní království (9 bodů)

Kuchařková úloha

Za devatero horami, sedmero moři a třemi informatiky na odvážné výpravě se rozkládá malé ostrovní království. I když je malé co do rozlohy, tak rozhodně není malé co do počtu ostrovů. Ostrovů je dokonce tolik, že v královském archivu ani pořádně neví, kolik jich je. Krále by nyní zajímalo, z kolika obydlených ostrovů (s alespoň jedním městem) se jeho říše skládá. Ale počet měst ani cest nikdo nezaznamenával.

Jedinou záchranou by mohlo být královské ministerstvo cest, které si drží podrobný přehled o všech cestách, o které se musí starat. Na každém ostrově se nachází několik měst (vždy minimálně jedno, menší ostrovy bez města nás teď nezajímají), každé z měst má své unikátní sekvenční číslo. Města na jednom ostrově jsou spojena cestami, které jsou také sekvenčně očíslované (číslujeme od nuly dál, žádná cesta ani žádné město ještě v historii království nezanikly, takže v číslování nejsou žádné „díry“).

Vždy platí, že ze všech měst na jednom ostrově se dá po cestách dostat do všech dalších měst na tom stejném ostrově, ale na jiný ostrov je potřeba vždy dojet lodí (zkrátka mezi ostrovy žádná cesta nevede, v království nevěří v existenci mostů). Navíc na žádném ostrově cesty netvoří cyklus (ministerstvo cest nebuduje zbytečné cesty a na existenci kruhových objezdů v království nevěří).

Na vás dopadl úkol spočítat počet ostrovů. Jediné dva typy dotazů, které můžete pokládat archivářům ministerstva cest, jsou:

Vyhledávání v archivu ministerstva cest je ale náročné (Už jsme se zmiňovali, že mimo mostů a kruhových objezdů nevěří v tomto království ani na papír? Záznamy jsou vytesány na masivních mramorových deskách…). Proto byste měli vymyslet postup, jak získat počet obydlených ostrovů na co nejméně dotazů do archivu.

Řešení

Teoretická úloha33-2-2 Hasičské stanice (11 bodů)

V právě postaveném městě inženýři zjistili, že zapomněli na jednu důležitou věc. Ve městě totiž nepostavili žádnou hasičskou stanici. Z vyhlášky EU však není dovoleno bydlet v budovách, které nejsou chráněné alespoň jednou hasičskou stanicí. Pomozte jim vymyslet, jak nejlépe stanice rozmístit.

Město si můžeme představit jako obdélník N×M budov. U každé budovy je dán maximální počet lidi, kteří zde mohou bydlet.

Každou budovu je možné přestavět na hasičskou stanici. Když se to stane, tak v dané budově již nebudou moct bydlet žádní lidé. Tato stanice pak bude chránit všechny budovy, které leží ve stejném řádku nebo sloupci (hasičská auta jsou moc veliká, a tedy nezvládnou zatáčet, aby dojela k budově za rohem).

Vaším úkolem je vymyslet algoritmus, který dostane zadanou mapu města a upraví ho přidáním hasičských stanic tak, aby byl počet lidí, kteří v něm mohou žít, co nejvyšší. Lidé mohou bydlet pouze v budovách chráněných alespoň jednou hasičskou stanicí a nemohou bydlet na hasičských stanicích.

Řešení

Praktická opendata úloha33-2-3 Bludiště s turrety (12 bodů)

Tajný agent Hrochbond uvízl v komplikovaném bludišti postaveném doktorem Zlounem. Bludiště je tvořeno pravoúhlými políčky, na kterých je buď prázdné místo, zeď, nebo turret střílející rakety jedním ze čtyř směrů. Agentovi Hrochbondovi se povedlo získat mapu bludiště a dokonce i intervaly, ve kterých jednotlivé turrety střílejí, a potřeboval by najít nejrychlejší cestu k východu.

Každý turret střílí pouze jedním směrem a to v pravidelných intervalech. V čase nula všechny turrety vystřelí raketu (objeví na sousedním políčku turretu ve směru jeho střelby) a rakety postupně letí rychlostí jednoho políčka za sekundu v přímém směru, dokud nenarazí na pevnou překážku (zeď, turret nebo Hrochbonda). Turret s intervalem K pak vystřelí další raketu za K sekund (tedy turret s intervalem K vystřelí raketu v časech 0, K, 2K, …).

Rakety jsou malé, takže pokud se potkají dvě rakety na stejném políčku, tak se vyhnou a obě letí dál v původním směru. Políčko turretu se počítá jako zeď jak pro Hrochbonda, tak pro rakety.

Ilustrace: Hrochbond v přestrojení

Hrochbond se zvládne přemístit na vedlejší políčko také za jednu sekundu, takže celý průchod bludištěm probíhá v jednosekundových kolech. Hrochbond se však nesmí vyskytnout na stejném políčku, na kterém se vyskytuje raketa (vybuchl by, k radosti doktora Zlouna), nebo na políčku, které raketa právě opustila (raketa má za sebou ohnivý plamen, který by z Hrochbonda udělal v mžiku well-done steak), a to i pokud raketa ihned po opuštění políčka narazí do zdi.

Hrochbond může vykonat každé kolo jednu z pěti následujících akcí:

Je možné vstoupit jen na volná políčka a na políčko cíle, zdmi a turrety procházet nelze.

Nalezněte pro zadanou mapu na vstupu nejrychlejší cestu (co do počtu kol) vedoucí ze startu do cíle bez toho, aniž by se Hrochbond během cesty dostal na políčko, na kterém se nachází raketa nebo se v minulém kole nacházela.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete tři čísla – R a S udávající počet řádků a sloupců mapy (pozice [0,0] je vlevo nahoře) a číslo T udávající počet turretů. Bude následovat R řádků po S znacích popisující bludiště: . (tečka) značí volné políčko, # zeď, T turret, S startovní pozici Hrochbonda a C cílové políčko.

Na následujících T řádcích pak dostanete popis jednotlivých turretů. Každý řádek bude obsahovat pozici turretu (řádek a sloupec, indexujeme od nuly), natočení turretu, ve kterém střílí rakety (jedno z písmen LPND), a interval ve kterém rakety střílí (interval bude mezi čísly 1 až 6 včetně).

Formát výstupu: Na první řádek výstupu vypište délku vámi nalezené nejkratší cesty D a na druhý řádek pak bez mezer D znaků udávajících jednotlivé Hrochbondovy kroky. Slibujeme, že cesta ze startu do cíle vždy existuje.

Ukázkový vstup: 
6 5 2
S....
#T...
....T
#.#..
.##..
.C..#
1 1 P 3
2 4 L 4
Ukázkový výstup: 
12
--PPPDDDDDLL

Animovaný příklad průchodu jiným bludištěm s turrety:

Pro zobrazení animace je potřeba JavaScript

Řešení

Praktická opendata úloha33-2-4 Oprava satelitů (13 bodů)

Na vesmírné stanici se kvůli nárazu s asteroidem pomíchaly satelity a je potřeba je srovnat. V extrémních podmínkách, které panují na této planetě, však nemá žádný astronaut šanci přežít – proto je potřeba naprogramovat robota, který závadu opraví autonomně.

Ilustrace: Ten správný robot na opravu satelitů

Satelity si lze představit jako orientovaný graf, kde z každého satelitu (vrcholu) vede jeden výstupní kabel (hrana). Na začátku robotovy práce tvoří satelity „řetěz“ se speciálními satelity Z na začátku a C na konci.

Robot začíná svojí práci na satelitu Z, může svoji práci ukončit kdekoliv a má k dispozici tyto čtyři typy příkazů:

Aby začala komunikace se Zemí opět fungovat, tak je potřeba pro robota připravit sérii příkazů, které po K-ticích satelity otočí pozpátku (vyjma krajních satelitů Z a C, které zůstávají na místě). Například pro K = 2 se má provést následující:

Z →1 →2 →3 →4→C
⇓
Z →2 →1 →4 →3→C

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku vstupu bude počet satelitů N (bez startovního a koncového) a velikost K-tic satelitů k otáčení. Slibujeme, že K dělí N (tj. nikde nezůstanou přebytečné satelity). V prvním testu je K = 2, ve všech ostatních je K ≥ 3.

Formát výstupu: Posloupnost příkazů, která každou sousední K-tici satelitů prohodí. Příkazy mají tento tvar:

Velikost programu pro robota může být nejvýše 50 MB (naše vzorová řešení dávají nejvýše malé jednotky MB).

Ukázkový vstup: 
2 2
Ukázkový výstup: 
P A
D
P B
D
P C
D
P D
T C
N B
T B
N D
T A
N C

Znázornění:

Z -> 1 -> 2 -> C
----------------
Z -> 1 -> 2 -> C
A    B    C    D
----------------
Z -> 2 -> 1 -> C

Body za poslední dva testy se odvíjí od toho, kolik různých značek robot na satelity položí – plné body lze získat pouze za řešení využívající nejvýše tři značky. Za použití více značek také nějaké body dostanete.

Na webu jsme připravili simulátor, ve kterém si řešení můžete otestovat. Po zadání instrukcí simuluje robotův pohyb po satelitech a v případě chyb zobrazuje také dodatečné informace, které by se mohly hodit při řešení úlohy.

Řešení

Bonusová úloha33-2-X1 Závody formulí (10 bodů)

Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.

Počítat se dá nejen klasickými algoritmy, ale třeba i pomocí logických (booleovských) formulí a obvodů. Pojďme se nad nimi zamyslet.

Formule

Nejprve definujeme formuli. To je výraz, ve kterém jsou logické proměnné (budeme značit řetězci písmen a číslic) pospojované logickými spojkami. Pro naše účely budou stačit spojky ∧ (and, konjunkce), ∨ (or, disjunkce) a ¬ (not, negace). Formule může například vypadat takto:

(x∧ ¬y) ∨ (¬x∧ y).

Když chceme formuli „spustit“, dosadíme za proměnné logické hodnoty 0 (nepravda) nebo 1 (pravda). Výstupem formule pak je jediný bit, opět 0 nebo 1. Vyzkoušejte si, že naše ukázková formule dostane x a y a spočítá jejich xor.

Nevýhodou formulí je, že „nemají proměnné“. Pokud chceme nějaký mezivýsledek použít víckrát na různých místech, nezbývá než zmáčknout pomyslné copy & paste a výpočet mezivýsledku zkopírovat. Pokud tento mezivýsledek závisí na jiném mezivýsledku a tak dále, může formule exponenciálně narůst. Proto budeme raději pracovat s obvody.

Obvody

Obvod se skládá z následujících součástek:

Jednotlivé součástky jsou propojené „dráty“ podle následujících pravidel:

Ukažme si příklad obvodu, který počítá xor podle naší formule:

Příklad obvodu

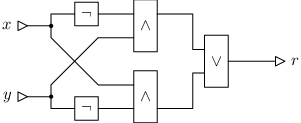
Výpočet obvodu probíhá v taktech. V každém z nich se aktivují ty součástky, které už mají k dispozici vstup z předchozích taktů, a vydají svůj výstup. V nultém taktu se tedy aktivují součástky, do kterých nevedou žádné dráty – to jsou vstupní porty a konstanty. Výpočet se zastaví, jakmile se aktivují všechny výstupní porty. Náš ukázkový obvod tedy počítá v pěti taktech: v nultém se aktivují porty x a y, v dalším negace, pak andy, pak or a nakonec výstup.

Všimněte si, že počet taktů výpočtu nezávisí na hodnotách vstupů. Můžeme ho také spočítat jako délku nejdelší cesty mezi vstupními porty (případně konstantami) a výstupními porty. Proto se mu říká hloubka obvodu. Hloubku můžeme považovat za analogii časové složitosti. Podobně můžeme měřit prostor potřebný na výpočet velikostí obvodu vyjádřené počtem hradel.

Pokud byste zatoužili prozkoumat obvody detailněji, doporučujeme seriál 20. ročníku. Pro tuto úlohu by to ale nemělo být potřeba.

Stromečky

K jedné formuli obvykle existuje více obvodů, které se mohou lišit hloubkou. Třeba pro x1 ∧ x2 ∧ … ∧ x8 můžeme spočítat x1∧ x2, pak výsledek z andovat s x3, pak výsledek s x4 atd. Takový obvod bude mít hloubku 9. Nebo můžeme vyrobit „stromeček z andů“:

Dva obvody pro AND 8 čísel

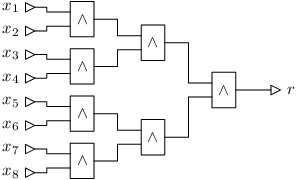
Ten spočítá totéž v hloubce 5. Obecně pro and n proměnných dá první způsob hloubku Θ(n), zatímco druhý Θ(log n).

Jak překládat formule

A teď konečně slíbená úloha. Budeme překládat formule na obvody. Dostaneme nějakou formuli délky n (délky budeme měřit řekněme počtem logických spojek) a budeme chtít vyrobit obvod, který počitá totéž s co nejmenší hloubkou.

Nějaký obvod určitě existuje. Stačí si nakreslit stromovou strukturu formule (v listech jsou proměnné, ve vnitřních vrcholech logické spojky. A to už vlastně je obvod, který počítá totéž: listy jsou vstupní porty (víc výskytů téže proměnné slepíme do jednoho portu), vnitřní vrcholy jsou hradla, z kořene vede drát do výstupního portu.

Tato konstrukce dává obvod hloubky Θ(n). Pro jeden konkrétní případ jsme ale viděli, že stačí Θ(log n). Uměli byste obecný převod vylepšit, aby se k tomu přiblížil? Zajímavé je libovolné řešení s lepší než lineární hloubkou.

Poznámka: Také se můžete zamyslet nad tím, jak překládat naopak obvody na formule. Jak velká formule vyjde? Bodovat to nebudeme, ale i tak budeme rádi, když nám to napíšete.

Řešení

Seriálová úloha33-2-S Šumy (15 bodů)

Toto je seriálová úloha, která navazuje na podobnou úlohu v minulé sérii. Pokud jste předchozí díl seriálu neřešili, pro pochopení tohoto dílu je dobré si jej nejméně přečíst. A pokud si chcete úlohy z minulého dílu také naprogramovat, stále za ně můžete získat polovinu bodů.

V tomto díle se podíváme na to, jak se dá z trošky náhody vytvořit něco zajímavého. Všechny přírodní struktury v sobě mají nějakou míru chaosu, ať už to je mech na skalách, oblaka na obloze, vzory ve dřevě nebo třeba povrch vašich dlaní. Právě náhodná podstata mnohých přírodních objektů dělá šumové funkce tak zajímavými a užitečnými. Nejprve si ale musíme nějakou tu náhodu pořídit.

Stejně jako v minulém díle budeme pracovat v Shadertoy, což je webový editor shaderů. Jak jej ovládat (a jak psát shadery) se dočtete v prvním díle seriálu.

Opět odevzdávejte zdrojové kódy vašich shaderů zabalené do zipka a pojmenované nějak tak, aby bylo jasné, který shader řeší kterou úlohu. Vždy prosím odevzdávejte celý spustitelný kód shaderu, ne jenom jeho část.

Náhoda

Vyrábět náhodné hodnoty v počítačích je poměrně problém, zvlášť pokud chcete náhodu využít pro kryptografii. My si ale vystačíme s něčím, co náhodně jen vypadá.

V běžných programovacích jazycích máme k dispozici pseudonáhodné funkce, které nám při každém zavolání vrátí jinou, zdánlivě náhodnou hodnotu, nicméně uvnitř jsou tyto funkce deterministické. Před prvním použitím bývají inicializovány nějakou počáteční hodnotou, takzvaným seedem. Pro stejný seed funkce vrací stejnou posloupnost hodnot. Pokud chceme, aby se náhodný generátor choval při každém spuštění programu jinak, můžeme jako seed použít například systémový čas.

V shaderech žádný podobný nástroj není. Už jen zajistit, aby každé volání nějaké funkce vracelo pokaždé jinou hodnotu je problém, protože různé pixely se nesmí navzájem ovlivňovat (protože se počítají paralelně). A pokud by náhodná funkce vrátila pro každý pixel to samé, tak by moc užitečná nebyla.

Naše náhodná funkce tedy bude muset mít nějaké parametry, minimálně souřadnice aktuálního pixelu, ze kterých „náhodu“ spočítá.

Chceme tedy něco, co pro málo se lišící hodnoty (například souřadnice sousedních pixelů) vrátí velmi různé výsledky. Tuto vlastnost mají hešovací funkce a jako zdroj náhody můžeme použít některou z nich. Také si můžeme jednu velmi jednoduchou hešovací funkci vyrobit ze staré dobré funkce sinus. Spusťte si následující shader:

float func(float x)
{
    float y = sin(x);
    //y = y * 10.0;
    //y = fract(y);
    return y;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    vec2 uv = fragCoord/iResolution.xy;
    // Střed souřadnic chceme uprostřed obrazu
    uv = uv * 2.0 - 1.0;
    // Korekce pro správný poměr stran
    uv.x *= iResolution.x / iResolution.y;

    vec3 col = vec3(0.0);

    // Rozsah obrazu je asi -4..4 v obou osách
    // (u X ve skutečnosti trochu jiný, aby byl
    // zachován poměr stran)
    uv *= 4.0;

    // Osa X
    col += clamp(1.0 - abs(uv.y) * 40.0, 0.0, 1.0) * vec3(1.0, 0.5, 0.5);

    // Osa Y
    col += clamp(1.0 - abs(uv.x) * 40.0, 0.0, 1.0) * vec3(0.5, 1.0, 0.5);

    // f(x)
    col += clamp(1.0 - abs(uv.y - func(uv.x)) * 20.0, 0.0, 1.0) * vec3(0.5, 0.5, 1.0);

    // Vybarvíme pozadí současnou hodnotou funkce
    col += clamp(func(uv.x), 0.0, 1.0) * 0.25;

    fragColor = vec4(col,1.0);
}

Shader zobrazuje graf funkce func, která je ve své neupravené podobě jen sinem. Pozadí je vybarveno hodnotou funkce pro x-ovou souřadnici daného pixelu.

Zkuste odkomentovat řádek y = fract(y); ve func a podívat se, jak se graf funkce změní. Funkce fract vrací desetinnou část čísla, existují i funkce floor vracející dolní celou část a ceil vracející horní celou část.

Nyní odkomentujte řádek y = y * 10.0;. Výsledek zatím nevypadá příliš zajímavě. Teď zvětšete konstantu 10.0, přidejte k ní pár nul. Výsledek pro třeba 10000.0 je poměrně chaotický, že? Právě jsme si vyrobili pseudonáhodnou funkci!

Poznámka: Toto demo je založené na podobné vizualizaci ve webové knize The Book of Shaders, kterou je inspirován i celý tento seriál. Neváhejte si ji přečíst, zvlášť 4. kapitolu, která je velmi zajímavá a relevantní k tomuto dílu seriálu.

Máme tedy něco, co nám z jednoho floatového parametru vyrobí „náhodu“. To ale nestačí. Vyrábíme dvojrozměrný obraz, a proto by se nám hodila funkce, která udělá náhodu z vec2. Tu vyrobíme následujícím trikem:

float random(vec2 st)
{
    float s = dot(st, vec2(12.3456, 34.1415));
    return fract(sin(s) * 45678.9);
}

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    vec2 uv = fragCoord/iResolution.xy;
    // Střed souřadnic chceme uprostřed obrazu
    uv = uv * 2.0 - 1.0;
    // Korekce pro správný poměr stran
    uv.x *= iResolution.x / iResolution.y;

    vec3 col = vec3(random(uv));

    fragColor = vec4(col, 1.0);
}

Z vektoru vyrábíme skalár tím, že provedeme skalární součin s nějakým konstantním vektorem. V tomto případě je to ekvivalentní (z definice skalárního součinu) zápisu float s = st.x * 12.3456 + st.y * 34.1415;. Pokud vám není jasné, co to skalární součin je, odpověď najdete v našem krátkém úvodu do vektorů.

Tedy změny jak v x-ové, tak v y-ové souřadnici vedou k jinému číslu dosazenému do sinu. Zároveň jsou obě čísla vynásobená různými a hlavně velkými konstantami, takže nevznikají čárovité artefakty (schválně zkuste místo toho použít vec2(1.0, 1.0)). Ve skutečnosti ty artefakty stále vznikají, jen jsou té správné velikosti a směru, že se v naší pravidelné mřížce pixelů neprojevují, a to nám stačí. Každý pixel padá do jiné části kopečků sinu. Kdybychom dostatečně zazoomovali, stále bychom artefakty viděli.

Neváhejte místo tohoto triku se sinem použít i jiné hešovací funkce. Spoustu jich naleznete například v tomto shaderu (přepněte se v editoru do záložky „Common“).

Perlin Noise

Náhoda je sice hezká, ale není až tak… hezká. Můžeme ji ale použít k vytvoření vizuálně zajímavější šumové funkce známé jako Perlin Noise či Perlinův šum.

Ideou Perlinova šumu je vytvořit pravidelnou mřížku bodů a spočítat náhodu jen pro tyto body. Pro místa mezi body interpolujeme (děláme plynulý přechod) hodnoty ze čtyř rohů aktuální „buňky“.

float random(vec2 st)
{
    float s = dot(st, vec2(12.3456, 34.1415));
    return fract(sin(s) * 45678.9);
}

float perlinNoise(vec2 st)
{
    vec2 cell = floor(st);
    vec2 cell2 = ceil(st);
    vec2 f = fract(st);

    float s00 = random(cell);
    float s01 = random(vec2(cell.x, cell2.y));
    float s10 = random(vec2(cell2.x, cell.y));
    float s11 = random(cell2);

    return mix(
        mix(s00, s10, f.x),
        mix(s01, s11, f.x),
        f.y
    );
}

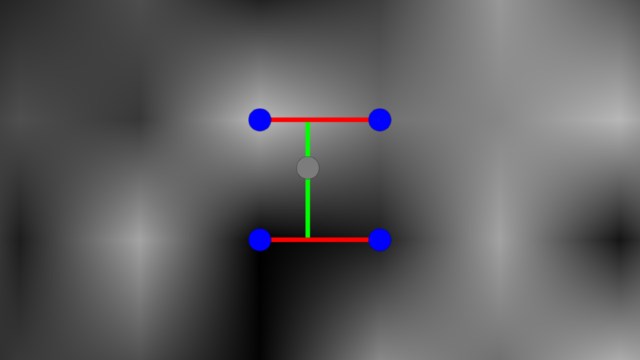
Naše buňky mají velikost jedné jednotky. Pro získání souřadnic rohu buňky používáme již zmíněnou funkci floor (dolní celá část) a pro souřadnice uvnitř buňky funkci fract (desetinná část). Poté si spočítáme náhodu ve všech čtyřech rozích buňky a hodnotu lineárně interpolujeme pomocí funkcí mix, nejdříve dle souřadnice x, poté dle y.

Obrázek vizualizuje funkčnost interpolace hodnot z rohů buňky. Modré puntíky značí rohy, ve kterých počítáme náhodu. Na červených horizontálních čarách interpolujeme podle x-ové souřadnice uvnitř buňky, poté mezi dvěma výslednými hodnotami interpolujeme podle y-ové osy. Celé to odpovídá kódu: mix(mix(s00, s10, f.x), mix(s01, s11, f.x), f.y). (Pamatujte, že mix(x, y, a) není nic jiného než x * (1 - a) + y * a.)

Zkuste tento šum spustit. Protože je velikost buňky jedna jednotka, je potřeba souřadnice pixelu něčím velkým vynásobit, aby bylo něco zajímavého vidět, třeba perlinNoise(uv * 16.0).

Toto zatím nevypadá nic moc – všimněte si kosočtvercových artefaktů. Ty jsou způsobeny právě lineární interpolací (občas je lze vidět i ve hrách, pokud má nějaká textura malé rozlišení). To opravíme tím, že použijeme místo křivky lineární křivku kubickou (v GLSL zabudovaná jako funkce smoothStep). Dejte před „mixování“ tento řádek: f = smoothstep(0.0, 1.0, f);. Výsledek už vypadá o něco lépe.

Gradient Noise

Existují různá vylepšení základního Perlinova šumu, například Simplex Noise nebo Gradient Noise. Simplex Noise používá místo čtvercové mřížky mřížku z rovnostranných trojúhelníků, což je pro vyšší dimenze výrazně rychlejší (počet bodů, co musíme spočítat, pak roste s dimenzemi lineárně, nikoliv exponenciálně).

Gradient Noise používá čtvercovou mřížku, ale neinterpoluje náhodné hodnoty jako takové, místo toho v každém vrcholu mřížky vytvoří nějaký přechod (gradient) a ten interpoluje. Více se o nich dočtete například v 11. kapitole The Book of Shaders.

Ve zbytku seriálu doporučuji používat místo základního Perlina právě jednu z těchto vylepšených variant. Níže je zdrojový kód pro Gradient Noise. Všimněte si, že náhodnou funkci, která místo skaláru vrací vec2, jsme vyrobili prostě tak, že náhodu počítáme dvakrát a vstupní st „dotujeme“ různými vektory, aby byly výsledky různé i pro stejné st.x a st.y. Také nyní v random2 vracíme hodnoty v rozsahu -1 až 1, což se nám pro Gradient Noise hodí.

vec2 random2(vec2 st)
{
    vec2 s = vec2(dot(st, vec2(12.3456, 34.1415)),
                  dot(st, vec2(42.2154, 15.2854)));
    return fract(sin(s) * 45678.9) * 2.0 - 1.0;
}

float gradientNoise(vec2 st)
{
    vec2 cell = floor(st);
    vec2 f = fract(st);

    vec2 s00 = random2(cell);
    vec2 s01 = random2(cell + vec2(0, 1));
    vec2 s10 = random2(cell + vec2(1, 0));
    vec2 s11 = random2(cell + vec2(1, 1));

    float d00 = dot(s00, f);
    float d01 = dot(s01, f - vec2(0, 1));
    float d10 = dot(s10, f - vec2(1, 0));
    float d11 = dot(s11, f - vec2(1, 1));

    vec2 u = smoothstep(0.0, 1.0, f);

    float noise = mix(mix(d00, d10, u.x), mix(d01, d11, u.x), u.y);
    return noise * 0.5 + 0.5;
}

Také si všimněte, že ve své základní variantě je Gradient noise docela šedivý a chybí mu kontrast. To lze opravit tím, že poslední řádek funkce gradientNoise nahradíte tímto: return clamp(noise * 0.8 + 0.5, 0.0, 1.0);. Hlavní rozdíl je v tom, že se hodnota noise při převodu na rozsah 0 až 1 násobí něčím větším než 0.5 a pokryje tedy větší rozsah hodnot. Nechceme ale omylem vybočit z rozsahu 0 až 1, proto ještě finální hodnotu „clampneme“ do tohoto rozsahu.

Cellular Noise

Dalším typem šumu je šum buňkový, anglicky známy jako Cellular Noise či Worley Noise. Jako u Perlina i zde rozdělíme plochu na čtvercové buňky. V každé buňce vygenerujeme jeden náhodný bod. Šum samotný je potom vzdálenost k nejbližšímu bodu (ať už leží v libovolné buňce).

vec2 random2(vec2 st)
{
    vec2 s = vec2(dot(st, vec2(12.3456, 34.1415)),
                  dot(st, vec2(42.2154, 15.2854)));
    return fract(sin(s) * 45678.9) * 2.0 - 1.0;
}

float cellularNoise(vec2 st)
{
    ivec2 cell = ivec2(floor(st));
    vec2 f = st - vec2(cell);

    float minDist = 1.0;

    for (int y = -1; y <= 1; y++)
    {
        for (int x = -1; x <= 1; x++)
        {
            ivec2 localCell = cell + ivec2(x, y);
            vec2 localPoint = random2(vec2(localCell)) * 0.5 + 0.5 + vec2(x, y);
            minDist = min(minDist, length(localPoint - f));
        }
    }

    return minDist;
}

Všimněte si, že stačí zkontrolovat jen 9 buněk pro každý dotaz – buňku aktuálního pixelu a osm sousedních.

Úkol 1 [3b]

Další zajímavou variantou této funkce je nevracet vzdálenost nejbližšího bodu, ale druhého nejbližšího. A právě to je vaším úkolem. Výsledek by měl vypadat nějak takto:

Fractal brownian motion

Ještě se podíváme na jedno velmi užitečné „šumové primitivum“. Na Perlin (či Gradient) Noise se dá dívat jako na „sinusoidu“. Kopečky sice mají různou velikost, ale rychlost změny hodnoty (frekvence) zůstává stejná. Co když sečteme několik šumů o různých frekvencích dohromady? Výsledek se nazývá Fractal brownian motion, zkráceně fbm. Kdyby byla suma nekonečná, skutečně by se jednalo o fraktál.

float fbm(vec2 st)
{
    float val = 0.0;

    float p = 0.5;

    const float angle = 1.0;

    mat2 rotation = mat2(
        cos(angle), sin(angle),
       -sin(angle), cos(angle)
    );

    for (int i = 0; i < 5; i++)
    {
        val += gradientNoise(st) * p;
        p *= 0.5;
        st *= 2.0;

        st += vec2(1.181, 0.57);
        st = rotation * st;
    }

    return val;
}

Ve funkci sčítáme několikrát Gradient Noise. Každá tato iterace se nazývá oktáva. Následující oktáva má vždy poloviční amplitudu (p *= 0.5;) a dvojnásobnou frekvenci (st *= 2.0;) než předchozí. Také souřadnice st v každé iteraci nějak posuneme a otočíme.

Výsledek této funkce by měl připomínat kouř či mraky. Zkuste ubrat nebo naopak přidat oktávy.

Úkol 2 [3b]

Dalším vaším úkolem je aplikovat stejný princip jako u fbm i na buňkový šum - sečtěte několik buňkových šumů o různých frekvencích. Výsledek je další užitečné „šumové primitivum“:

Úkol 3 [3b]

Zkuste co se stane, když do sebe „zapojíte“ tři fbm.

Bude potřeba vytvořit si vlastní „barevnou“ verzi funkce fbm, která nevrací jedinou hodnotu, ale alespoň vec2, aby šla přičítat k souřadnicím. Také je lepší, když tato hodnota bude v rozsahu -1 až 1 místo 0 až 1. Ve skutečnosti se hodí, aby vracela rovnou vec3, ve vnitřních funkcích z něj použijeme jen první dvě složky a ve vnější z něj získáme barvu (nezapomeňte ji převést do rozsahu 0 až 1).

Též můžete výsledky některé z vnořených fbm něčím pronásobit, aby měly větší vliv na vnější fbm.

Také lze místo některé fbm použít vícevrstvý buňkový šum (opět upravený na barevný) z předchozího úkolu.

Úkol 4 [2b]

Animujte (posunujte) souřadnice uv z předchozího úkolu v čase. Zkuste souřadnice v různě vnořených fbm (či Worleyho šumech) animovat různě rychle a různým směrem.

Úkol 5 [4b]

Vraťme se k základnímu buňkovému šumu. Co když jako zdroj pozic bodů v buňkách použijeme místo úplné náhody (random2) něco sofistikovanějšího, třeba fbm? Ve statickém obrázku se nich moc nestane, proto zkuste pozice těchto bodů animovat v čase (třeba posunujte souřadnice, ze kterých se čte fbm). Navíc z buňkového šumu vracejte, který bod byl nakonec nejbližší a různé buňky poté různě obarvěte.

Tím jsme si prošli základní šumové funkce. Jak jsme zmínili na začátku, jejich využití je především procedurální generování různých (nejen) přírodních útvarů. A na to, jak se něco takového dělá, se lépe podíváme v příštím díle. Také se v příštím díle podíváme, jak se zhruba chová světlo a jak naše výtvory nasvětlit.

Kuba Pelc

Řešení