Třetí série třicátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 33-3-1: Bezpečný tunel
- 33-3-2: Ospalý student a diktát
- 33-3-3: Stříbrných stříkaček
- 33-3-4: Obsazování území
- 33-3-S: Světlo a stín
- 33-3-X1: Z(a)tracené kouzlo
 33-3-1 Bezpečný tunel (Zadání)
33-3-1 Bezpečný tunel (Zadání)
Chceme najít nejkratší cestu mezi políčky, na která se umí legálně dostat Kevin, a políčky, na která se legálně umí dostat Zuzka. Nejdříve tedy najdeme, jaká políčka to vůbec jsou: spustíme prohledávání do šířky se startem v Kevinově domě, navštívená políčka si označíme, a pokud se dostaneme do vzdálenosti více než K metrů, skončíme. To samé provedeme se startem v Zuzčině domě.
Jak nyní najít dvě různě označená políčka, která jsou k sobě nejblíž? Použijeme prohledávání do šířky ještě jednou. Tentokrát však ne se startem v jediném bodě, ale za startovní políčka prohlásíme všechna políčka, na která se umí dostat Kevin. Tato políčka vložíme do fronty, nastavíme jim nulovou vzdálenost a pokračujeme standardním prohledáváním do šířky, ignorujícím zdi, dokud nenarazíme na první políčko, na které se umí dostat Zuzka. Toto bude druhý konec tunelu, ten první můžeme najít, když si během prohledávání budeme ukládat zpětné odkazy a pak po nich projdeme do jednoho z políček, odkud jsme prohledávání začali.
Jaká bude časová složitost tohoto algoritmu? Používáme třikrát za sebou prohledávání do šířky a pak ještě jednou projdeme některá políčka. Prohledávání do šířky na čtvercové mapě s rozměry M ×N nám zabere O(M N) času, stejně jako následné procházení políček. To bude tedy výsledná časová složitost. Samotné načítání mapy do paměti zabere O(M N) času, lepší algoritmus tedy nenajdeme.
Co kdybychom však mapu v paměti mít nemuseli a načítali jen políčka, která potřebujeme? Začneme stejně, najdeme si políčka, na která se Kevin a Zuzka umí dostat. Těchto políček je O(K2), prohledáváním do šířky to zvládneme v čase O(K2). Nyní předpokládejme, že Kevinův dům je víc vlevo než Zuzčin dům. Nechť souřadnice nejpravějšího políčka, na které se Kevin umí dostat, je xK, a souřadnice nejlevějšího políčka, na které se umí dostat Zuzka, je xZ = xK + c. V takovém případě libovolný tunel, který Zuzka s Kevinem vykopou, musí jít alespoň c políček vodorovným směrem. Můžeme si tedy Zuzčin dům a všechna políčka, na která se umí dostat, pomyslně posunout o c políček doleva. To samé uděláme i se svislým směrem a ypsilonovou souřadnicí. Takto si můžeme mapu zmenšit na velikost O(K) ×O(K) a opět stejným způsobem najít oba konce tunelu. Časová i paměťová složitost bude v takovém případě O(K2).
 33-3-2 Ospalý student a diktát (Zadání)
33-3-2 Ospalý student a diktát (Zadání)
Pohlédněme na úlohu grafově. Délka úkolu n odpovídá počtu vrcholů a každý útržek popisuje orientovanou cestu na těchto vrcholech. Když tedy rozdělíme útržky na hrany, dostaneme nějaký orientovaný graf. V něm pak chceme najít jednoznačné pořadí jeho vrcholů tak, aby vedly orientované hrany vždy z vrcholu s nižším pořadím.
Jinými slovy, graf chceme topologicky setřídit. Aby toto setřídění existovalo, v grafu nesmí existovat žádný orientovaný cyklus. Nahlédněme, že pokud by takový cyklus existoval, tak ať už zvolíme na tomto cyklu libovolný vrchol jako první v pořadí, bude do něj vést hrana nesprávným směrem. Takové grafy nazýváme orientované acyklické grafy nebo též DAGy (zkratka z anglického názvu).
Je potřeba, aby hran v grafu bylo alespoň n-1. Kdyby ne, graf bude určitě nesouvislý. Pořadí vrcholů z různých komponent lze libovolně prohazovat, tím pádem nemůže být jednoznačné.
Všimněme si, že každý DAG musí obsahovat vrchol s, do kterého nevede žádná hrana. Kdyby tomu tak nebylo, najdeme orientovaný cyklus: začněme v libovolném vrcholu s0. Do vrcholu si vede hrana, vydejme se tedy „pozpátku“ po ní do si+1. Tohle můžeme opakovat, dokud z sℓ nenarazíme na již navštívený vrchol sk. Orientovaný cyklus je tedy sk →sℓ →… →sk+1 →sk.
Pokud vrchol s bez vstupních hran existuje jen jeden, můžeme ho bezpečně prohlásit za první v pořadí. Pokud najdeme alespoň dva různé vrcholy bez vstupních hran, rovnou prohlásíme, že tyto vrcholy nemají jasné pořadí. Pokud žádný vrchol bez vstupních hran nenajdeme, vyskytuje se v grafu orientovaný cyklus, který můžeme třeba pomocí DFS najít a vypsat.
Pokud z DAGu odstraníme libovolný vrchol v, dostaneme znovu DAG, a v něm bude jistě existovat jiný vrchol s' bez vstupních hran. Obdobně, pokud graf obsahuje orientovaný cyklus C, vrchol s jistě nebude jeho součástí a jeho odstranění C nepřeruší.
Takto můžeme topologicky třídit. Začínáme s prázdným pořadím na původním grafu. Pokud najdeme s1 ≠ s2 bez vstupních hran, rovnou prohlásíme, že s1 a s2 nemají jasné pořadí. Pokud žádné s nenajdeme, můžeme třeba pomocí DFS najít orientovaný cyklus a ten vypíšeme. Jinak přidáme jednoznačné s do rozpracovaného pořadí, odstraníme jej z grafu a pokračujeme dál stejným způsobem, dokud neurčíme pořadí všech vrcholů.
Tohle nám jistě dává algoritmus, který najde správné pořadí. Pokud by graf nebyl DAG, tak na orientovaný cyklus dříve či později narazíme tím, že nenajdeme s. Stejně tak pokud by bylo pořadí nejednoznačné, tak někdy narazíme na více různých s1 ≠ s2 v nějakém podgrafu.
Pokud tento algoritmus však naprogramujeme takto přímočaře, bude mít časovou složitost Ω(n2). Nejvíce nás totiž zdržuje nalezení s, které prochází všechny vrcholy n-krát. Naštěstí každé odstranění vrcholu sníží počet vstupních hran jeho sousedů o 1.
Stačí si tudíž udržovat u každého vrcholu počet aktivních vstupních hran a seznam výstupních hran. Kromě toho chceme udržovat seznam vrcholů s nula aktivními hranami, označme jej S. Zpočátku pro každý vrchol nastavíme počet aktivních hran na počet vstupních hran. Vrcholy, které nemají žádné vstupní hrany, přidáme do S rovnou. To uděláme jednoduchým průchodem všech vrcholů.
Poté n-krát zopakujeme určení i-tého vrcholu v pořadí: Podíváme se na délku seznamu |S|. Pokud |S| ≠ 1, prohlásíme patřičný problém. Jinak vrcholu s ∈S určíme pořadí i, všem jeho výstupním sousedům snížíme počet aktivních hran o 1 a smažeme jej z S. Sousedy, kterým klesl počet aktivních hran na 0, přidáme do S.
Každý krok trvá O(1 + d), kde d je počet hran vycházejících z aktuálního s. Všech n kroků se pak sečte na čas O(n + m) = O(m), kde m je počet hran.
Zbývá dořešit, jak převést vstup na graf. Každý útržek rozdělíme na hrany a přidáme je příslušným vrcholům. Ještě musíme ověřit, že ve všech útržcích dohromady bylo opravdu n různých čísel. Pokud ne, nahlásíme chybu. Celý algoritmus pak bude mít složitost O(N), kde N je délka vstupu – součet délek všech útržků.
Zatím jsme však stále neřešili, jak indexovat vrcholy. Pokud jsou vrcholy dostatečně malá přirozená čísla v rozsahu O(n), můžeme je třeba indexovat v poli. To ale nemusí platit – čísla mohou být třeba obrovská, záporná nebo desetinná, žádnou bližší vlastnost jsme neslíbili. Není však problém v čase O(n log n) vstup přečíslovat na čísla 1,…,n.
 33-3-3 Stříbrných stříkaček (Zadání)
33-3-3 Stříbrných stříkaček (Zadání)
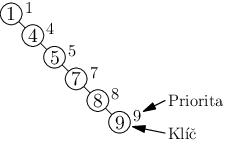
Budeme využívat názvosloví treap. Tedy dostřik bude klíč a náhodná čísla budou priority.
Vždy budeme chtít odpovídat maximálním možným počtem čísel, co jde, tedy N.
Na první vstup stačí odpovědět 3 1 2.
Prvním přidáním se dvakrát zavolá split a dvakrát merge (bez
žádné rekurze). Druhým pak čtyřikrát a třikrát (každý split zavolaný
z main dostane neprázdný vstup, tedy alespoň jednou zavolá sám sebe a
jeden merge zavolá také sám sebe, protože oba dva parametry budou
neprázdné treapy). Posledním pak alespoň čtyřikrát a čtyřikrát (každé volání
z main se alespoň jednou zrekurzí).
Celkem tedy funkce budou zavolány alespoň 21krát bez ohledu na náhodná čísla.
Toto byl jen cvičný vstup na uvědomění si fungování treapu.
Dále si povšimneme, že spoustu volání funkcí na jedno číslo dostaneme tehdy, když budeme pracovat se stromy s velkou hloubkou. Je tedy vhodné, aby se strom nijak nevětvil, tedy aby se jednalo o cestu. Cestu získáme třeba tak, že každý vrchol bude mít stejnou hodnotu jako váhu. Pro získání nějakých bodů tedy stačí odpovědět stejná čísla, jako byla na vstupu.
První problém tohoto řešení nastane, když generátor náhodných čísel bude rozbitý a bude vracet opakovaně stejná čísla. Naše řešení tedy nebude vytvářet nové vrcholy treapu. Stačí se ale podívat na přesnou implementaci treapu a povšimnout si, že při rovnosti vah se nahoru dostane levý vrchol, tedy při dalších výskytech stejného čísla stačí odpovědět o trošku větším číslem. Díky tomu vznikne nový vrchol a stále zůstane zachován tvar cesty.
Díky tomu ale bude nutné všechna čísla přečíslovat. Tedy každé prioritě na vstupu přiřadit unikátní klíč mezi 0 a N-1 tak, aby se nezměnilo uspořádání. Tedy když priorita na pozici a je menší než priorita na pozici b, tak musí být i klíč na pozici a menší než klíč na pozici b. Pro rovnající se priority musí být klíče setříděné podle výše popsaného pozorování.
Setřídíme si dvojice (priorita, index) podle priority a v případě rovnosti podle indexu. Tuto posloupnost projdeme a postupně jí přiřadíme čísla klíčů od 0 do N-1. Poté, například pomocí setřídění podle indexu, přejdeme k původnímu pořadí.
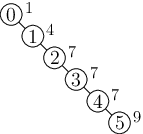
Když bude náhodný generátor generovat klesající posloupnost, dosavadní řešení také nebude fungovat. Vždy totiž připojí nový vrchol nad původní kořen pomocí malého počtu volání funkcí.
Vzorové řešení tedy z poloviny čísel vytvoří předchozím algoritmem treap ve tvaru cesty. Zbylým prioritám určí hodnotu tak, aby byla těsně za posledním vrcholem této cesty. Díky tomu algoritmus musí rozdělit treap tak, že projde celou cestu.
Počet operací tedy musí být větší než 2 ·(N/2) ·(N/2).
Přidáním každého z N/2 vrcholů v druhé skupině se provede alespoň N/2 operací
split a následně merge.
S tímto řešením již vyřešíme všechny vstupy.
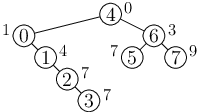
 33-3-4 Obsazování území (Zadání) (Komentáře)
33-3-4 Obsazování území (Zadání) (Komentáře)
Úloha s nakupováním domů na mapě a obsazováním území byla netradiční, ale o to zajímavější. Stala se velmi populární i mezi organizátory, kteří se společně s účastníky předháněli v tom, komu se povede pokrýt všechny zastavěné plochy za co nejméně peněz.
Tato úloha patří mezi ty, na něž je těžké najít optimální řešení. Velikost stavového prostoru roste exponenciálně (i když se dá velmi dobře prořezávat) a mapa už je moc velká na to, aby šlo vyzkoušet všechny možnosti. Taková úloha se řeší heuristicky – nehledáme nejlepší možné řešení, ale pokoušíme se odhadnout nějaké, které alespoň nebude vyloženě špatné.
Řešení této úlohy tedy pojmeme tak, že se pokusíme ukázat několik různých heuristických přístupů, které používali organizátoři. Je poučné se podívat na různé přístupy k tomu samému. Zároveň jsme požádali i několik nejlepších řešitelů, aby také sepsali své postupy řešení, můžete si je přečíst v komentářích k řešení.
Nejdříve trocha statistiky. Mapa Fiktivní Prahy sestávala celkem ze 268 435 456 (228) políček. Domů (zastavěných políček) bylo 21 295 829 (necelých 8 procent všech políček), a kdyby se někdo rozhodl koupit všechny, tak by ho to stálo neuvěřitelnou částku 114 338 661 881.
Nejlepší nalezené pokrytí Fiktivní Prahy bylo pokrytí 332 domy za celkovou cenu 532 293, za orgy těsně uhájil první místo Jirka Sejkora. Nejlepší účastnické pokrytí od Kristýny Petrlíkové skončilo těsně v závěsu s 329 domy za celkovou cenu 532 824.
Protože získat řešení s cenou blížící se jednomu milionu bylo celkem jednoduché a obtížný byl přesun od jednoho milionu k půl milionu, nastavili jsme bodovací funkci tak, že zhruba do 1 200 000 body přibývají pomalu a od této chvíle se počet bodů zvedá. Počet získaných bodů pro celkovou cenu C je:
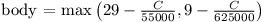
Maximální počet bodů jsme zastropovali na 15 a tímto gratulujeme Kristýně k jejich získání. Dosažené ceny a body ostatních (včetně organizátorů) si můžete prohlédnout v tabulce výsledků.
Nyní již následují jednotlivá řešení. Na konci řešení pak naleznete jejich vizualizace a porovnávač.
Řešení Jirky Kalvody
Svůj plánek Prahy jsem si nejprve rozdělil na 8 svislých sloupců a každý jsem řešil samostatně. Doufal jsem, že překryvy na hranicích řešení moc nezdraží a díky rozříznutí stačilo vyřešit mnohem menší vstupy.
Každý vstup jsem pak procházel z vrchu dolů. V každý moment jsem si pamatoval několik možností, jak pokrýt již navštívené budovy. Pro každou budovu, kterou jsem potkal, jsem prošel všechny tyto možnosti pokrytí. U těch, které aktuální budovu nepokrývaly, jsem vyzkoušel různé možnosti, jak ji pokrýt, tedy koupit budovu v okruhu 500 metrů. Tím jsem jedno možné pokrytí nahradil několika novými, které již danou budovu pokryjí.
Takto by stačilo projít celý plánek a na konci vybrat pokrytí, které je nejlevnější. Ovšem je tu problém. Počet pokrytí při tomto algoritmu roste moc rychle, takže by nám brzy došla paměť, a navíc by algoritmus asi nestihl doběhnout v dosažitelném čase. Proto je nutné možnosti průběžně omezovat a vybírat ty nejnadějnější. Jenže jak na to? Každou možnost jsem se pokusil nějak ohodnotit a pak vybrat jen určitý počet těch nejlepších. Zde již nejspíše neexistuje žádný exaktní algoritmus ohodnocení, a proto přichází na řadu heuristika.
Levnější možnosti by mohly být lepší než dražší. Ale také záleží na tom, kolik domů (a taky které) krom již navštívených pokryje. Já jsem se proto rozhodl od ceny domu odečíst jednu k-tinu ceny pokrytých domů. Za k jsem zkoušel dosazovat různá čísla a pro každé jsem vybral několik nejlepších možností. Další možnosti jsem pak vybíral náhodně.
Každou z osmi oblastí jsem se tímto algoritmem pokusil vyřešit několikrát (s různým generátorem náhodných čísel). Pro každou oblast jsem pak vybral nejlepší řešení a ta jsem pak spojil.
Algoritmus po chvíli našel řešení s cenou 740 391.
Řešení Kuby Pelce
Nejdříve jsem zkusil přímočaré hladové řešení: postupně procházím všechna políčka, zleva doprava, shora dolů, a každý nepokrytý dům koupím. Výsledná cena je 3 174 465.
Tento hladový algoritmus jsem trochu vylepšil: když narazím na nepokrytý dům, najdu ten nejlevnější dům, který ho dokáže pokrýt, a ten koupím (bez ohledu na to, jestli už sám je nebo není pokrytý). Tímto postupem se lze dostat pod million, tento postup našel pokrytí za cenu 908 980.
Poté jsem vyzkoušel spoustu různých věcí, které ale příliš nepomohly. Například jsem domy kupoval podle jejich „cenavýkonu“, tedy poměr mezi jejich cenou a cenou všeho, co by koupě tohoto domu pokryla.
Nejlépe fungovalo randomizované řešení s poměrně jednoduchou myšlenkou: koupím mnoho náhodných domů (mnohem více, než jich je na pokrytí celého města potřeba), poté všechny zbytečné domy zahodím.
Moje generování náhodných domů ale není úplně přímočaré. Nejdříve vyberu náhodný bod na mapě. Tento bod nemusí odpovídat žádnému domu. Poté najdu dům co možná nejbližší k tomuto bodu. K tomu jsem použil předpočítanou mapu (pomocí BFS), která mi pro každé pole říká, kterým směrem se posunout, abych se přiblížil k nějakému domu. Nakonec v nějakém čtverci okolo takto nalezeného domu vyberu ten nejlevnější dům a ten koupím.
Abych měl zaručeno, že tato množina náhodně koupených domů skutečně pokryje celé město, všechny nepokryté domy pokryji pomocí předchozího hladového algoritmu.
Nyní vím, že tato množina pokrývá celé město, ale také obsahuje spoustu zbytečných domů, které je třeba nějak zahodit.
Pro každé políčko mapy si spočítám, kolikrát je množinou pokryto. Poté projdu všechny domy množiny od nejdražšího po nejlevnější. Pokud pro nějaký koupený dům platí, že všechny domy, které pokrývá, jsou pokryty více než jednou, tak daný dům zahodím, protože i potom bude stále pokryto celé město.
Tímto algoritmem jsem se dostal na cenu 665 550.
Řešení Jirky Sejkory
Můj přístup je založený na vylepšování už existujících řešení. Kombinací různých postupů jsem došel až k řešení s cenou 532 293.
Celou dobu jsem udržoval databázi řešení, která na konci obsahovala 21 730 řešení s celkovým počtem 7 601 772 domů.
Detailní popis včetně zajímavých optimalizací a zdrojových kódů je dostupný v Gitovém repozitáři. Následuje jen velmi zběžné shrnutí popisu z předchozího odkazu.
Prvotní generování řešení bylo plně náhodné a později se při generování začal brát ohled na již existující řešení. Domy z dobrých řešení měly větší pravděpodobnost na vybrání do řešení.
Náhodně vygenerovaná řešení jsem zlepšoval pomocí přesunů domů na levnější místa a spojováním dvojic domů v jeden. Tyto přesuny vždy zachovaly validitu řešení. Jak to dělat efektivně (v lineárním čase s počtem pokrytých políček) je popsáno v detailní verzi.
Taktéž jsem kombinoval 1500 až 3500 nejlepších řešení pomocí vertikálních a horizontálních řezů, pokud zachovaly validitu řešení. Toto vyžadovalo netriviální množství optimalizací, aby to doběhlo v rozumném čase. Finální verze to zvládala za deset až dvacet minut.
A jako poslední hlavní část jsem vyřezával z nejlepšího řešení podměsto, které jsem optimalizoval samostatně a poté sloučil opět zpátky.
Tyto přístupy jsem různě střídal a ručně vybíral, které části má smysl vyřezávat.
Celkově řešení spotřebovalo přibližně týden čistého času plného vytížení jednoho procesoru s 12 vlákny a v některých momentech jsem měl problém vejít se do 32 GB paměti — což by šlo výrazně vylepšit za cenu menší rychlosti.
Po všech optimalizacích ale věřím, že k podobně dobrému řešení lze dojít znovu za jednotky hodin.
Vizualizace řešení
Pomocí seznamů nalevo a napravo můžete vybírat řešení k porovnání.

 33-3-X1 Z(a)tracené kouzlo (Zadání)
33-3-X1 Z(a)tracené kouzlo (Zadání)
Nejprve si připomeneme, jak v nějakém řetězci kouzlo najít. Použijeme algoritmus Knuth-Morris-Pratt neboli KMP. Ten vytvoří automat. To je graf, jehož stavy (vrcholy) odpovídají prefixům kouzla. Mezi stavy vedou dva druhy hran: dopředné, které prodlužují prefix o jeden znak, a zpětné. Ty pro každý prefix kouzla určují, jaký nejdelší jeho neúplný sufix je také prefixem kouzla.
Celým řešením nás bude provázet příklad ze zadání:
Máme abecedu { A, B, C },
spočítejme všechny řetězce délky N=5 se zaklínadlem AAA respektive ABC.
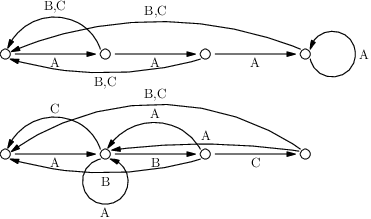
Automaty algoritmu KMP vypadají takto:

Pomocí hran se pak při čtení řetězce pohybujeme mezi stavy. Aktuální stav vždy určuje, jaký nejdelší sufix již prošlého řetězce je prefixem hesla. Když další písmeno řetězce odpovídá dopředné hraně, tak se po ní posuneme. V opačném případě se pohybujeme po zpětných hranách do té doby, než bude předchozí podmínka splněná, anebo již žádná zpětná hrana nebude existovat. Pro nás je ovšem nepraktické uvažovat dva typy hran, tak se jich pojďme zbavit.
Vytvoříme jiné hrany, které budou přímo reprezentovat přechody mezi stavy KMP. Pro každý stav a každé písmenko je totiž jednoznačně určeno, do jakého stavu se dostaneme. V původním KMP se tam dostaneme nějakou posloupností zpětných hran a nejvýše jedné dopředné. Ale my celou tuto posloupnost nahradíme jedinou hranou označenou příslušným písmenem abecedy. Tím vznikne multigraf – může mít paralelní hrany a může obsahovat smyčky. (Mimochodem, pokud znáte konečné automaty, přesně takový jsme teď popsali.)
Nové hrany můžeme vytvořit indukcí podle stavu (od prázdného prefixu k celému kouzlu). Z prázdného prefixu povede dopředná hrana označená prvním písmenem kouzla. Pro ostatní písmena kouzla zřídíme smyčky vedoucí zpět do počátečního stavu. Pro každý další stav ponecháme dopřednou hranu a všechny ostatní hrany zkopírujeme z toho stavu, do kterého v KMP vedla zpětná hrana.
Pro naše příklady to dopadne takto:
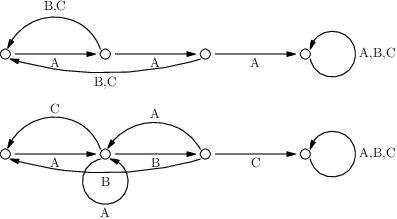
Ještě si ale tento graf mírně upravíme. Zajímá nás totiž jen, jestli řetězec kouzlo obsahuje či nikoliv. Je nám jedno, kde přesně výskyty jsou, ani kolik jich je. Proto stav „právě jsme na konci kouzla“ nahradíme stavem „už jsme celé kouzlo alespoň jednou našli“. Z tohoto stavu se v průchodu již nikdy nedostaneme. Stačí tedy vzít původní koncový stav a hrany nahradit smyčkami, které se vrací zase do tohoto stavu:
Teď se konečně dostaneme k zadané úloze. Ta vůbec nechce zjistit, zdali nějaký řetězec obsahuje kouzlo – místo toho nás zajímá, kolik takových řetězců existuje. Pojďme tedy prohledávání spustit na všech řetězcích současně.
Uvědomíme si, že výpočet našeho vyhledávacího algoritmu pro nějaký řetězec odpovídá právě jedné procházce (sledu) po předchozím grafu. Ta vede z počátečního stavu (prázdného prefixu) přes hrany označené postupně písmeny řetězce. A pokud jsme našli kouzlo, procházka skončí v koncovém stavu.
Řetězce délky N obsahující kouzlo tedy přesně odpovídají procházkám délky N v tomto grafu, které začínají v počátečním stavu a končí v koncovém. Za různé procházky přitom považujeme ty, které se liší v alespoň jedné hraně po cestě (nestačí rozdílnost ve vrcholech, protože více hran může spojovat stejné vrcholy).
Toto vyřešíme pomocí dynamického programování. Pro každou délku procházky budeme počítat, kolik existuje různých procházek končících v každém stavu. Při zvyšování délky procházky pak jen projdeme všechny hrany grafu. K cílovým vrcholům pro procházku délky n+1 přičteme hodnoty počátečních vrcholů procházky délky n. Odpověď pak bude počet procházek délky N hran končících ve stavu „obsahuje kouzlo“.
Opět příklad:
| Délka | 0 | 1 | 2 | 3 | 4 | 5 |
"" | 1 | 2 | 6 | 18 | 52 | 152 |
"A" | 0 | 1 | 2 | 9 | 18 | 52 |
"AA" | 0 | 0 | 1 | 3 | 6 | 18 |
| Obsahuje | 0 | 0 | 0 | 1 | 5 | 21 |
| Délka | 0 | 1 | 2 | 3 | 4 | 5 |
"" | 1 | 2 | 5 | 14 | 40 | 115 |
"A" | 0 | 1 | 3 | 9 | 26 | 75 |
"AB" | 0 | 0 | 1 | 3 | 9 | 26 |
| Obsahuje | 0 | 0 | 0 | 1 | 6 | 27 |
Abychom nenaráželi na velikost datových typů, celý výpočet budeme provádět modulo velké prvočíslo P.
Výsledky dynamického programování můžeme průběžně zapomínat. Stačí si jen pamatovat aktuální a předešlou délku řetězce.
Časová složitost algoritmu je O(AZN), kde A je velikost abecedy, Z délka kouzla a N délka řetězce. Paměťová složitost je O(AZ).
Zrychlujeme
Dále si všimneme, že každá počítaná hodnota pro nějak dlouhý řetězec je jen lineární kombinací počítaných hodnot pro o jedna kratší řetězec. To můžeme popsat pomocí násobení matic. Uvážíme sloupcový vektor xn, který odpovídá počtům procházek délky n do jednotlivých stavů. Pokud tento vektor vynásobíme zleva vhodnou maticí, dostaneme vektor xn+1 počtů procházek délky n+1 do jednotlivých stavů. Hodnoty v této matici budou odpovídat koeficientům lineárních kombinací z předchozího algoritmu – rozmyslete si, že nám vlastně budou říkat, kolik hran vede z i-tého stavu do j-tého. Je to tedy multigrafová obdoba matice sousednosti.
Máme tedy matici A takovou, že Axn = xn+1. Proto xN = ANx0, kde x0 je vektor počtů procházek o 0 hranách (má tedy 1 v počátečním stavu a všude jinde 0.
Pro naše příklady:
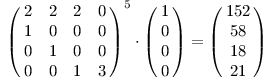
AAA je 21.
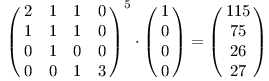
ABC je ale 27.
Teď stačí využít standardní algoritmus pro výpočet N-té mocniny pomocí O(log N) násobení. Ten funguje pro matice stejně jako pro čísla, takže AN spočítá pomocí O(log N) maticových násobení. Jelikož násobíme matice (Z+1)×(Z+1), jedno násobení trvá O(Z3). Celý algoritmus proto seběhne v čase O(Z3 log N) a paměti O(Z2).
(Můžete se podivovat, kam se poděla závislost na velikosti abecedy. Té jsme se dovedli zbavit proto, že všechny znaky, které se nevyskytují v zaklínadle, můžeme považovat za „ostatní“ a vždy si pořídit příslušný počet paralelních hran v grafu.)
 33-3-S Světlo a stín (Zadání)
33-3-S Světlo a stín (Zadání)
Odkazy na referenční implementace úkolů ze všech dílů seriálu naleznete v řešení posledního dílu seriálu.