Pátá série dvacátého osmého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu pošleme každému, kdo získá z alespoň šesti úloh alespoň dva body.
Zadání úloh
Tento příběh završuje příběhy uplynulých sérií. Pokud vám něco nebude dávat
smysl, přečtěte si minulé díly :-)
* * *
Will Knight, vedoucí výzkumník časoprostorového výzkumu, se vrávoravě sebral
se země a oprášil ze sebe saze. Ještě než k němu skrz zalehlé uši dolehlo
houkání sirén, viděl, jak všechno kolem zběsile bliká. To nebude dobré,
pomyslel si.
„Wille, jsi v pohodě? Wille?!?“ ozýval se neodbytně hlas z interkomu. Will
hrábl po tlačítku a přitom se rozhlížel okolo. To, co si v dalších minutách
poskládal ze svých vzpomínek, ze stavu okolí a z toho, co mu řekli z druhé
strany spojení, nebylo vůbec dobré.
Tohle měl být první experiment, kdy časem pošlou člověka, konkrétně Willa. Zatím
vyslali jen několik automatických sond. Ale asi selhal časoprostorový generátor
a jádro generátoru, ve kterém se teď Will nacházel, se už vůbec nenacházelo ve
stejném čase jako zbytek jeho týmu. Nikdo vlastně nevěděl, kde (a kdy) se
ocitlo. Jediné, co měli k dispozici, byly údaje z několika časových majáků ve
stěnách generátoru a spojení přes časoprostorový interkom.
 28-5-1 Zaměřování místnosti (9 bodů)
28-5-1 Zaměřování místnosti (9 bodů)
Výzkumný tým získává souřadnice od časoprostorových majáků
instalovaných ve stěnách místnosti posunuté v čase. Bohužel přijímají více sad
údajů a potřebují rychle odlišit, které sady souřadnic jsou chybné a které by
skutečně mohly označovat místnost.
Výzkumníci ví, že místnost má obdélníkový tvar a majáky jsou instalované
v jejích stěnách. Od vás by potřebovali pomoc s tím, jak rychle určit, jestli
všechny dané body leží na nějakém (jakkoliv otočeném) obdélníku, nebo ne.
Souřadnice bodů jsou libovolná reálná čísla, zaokrouhlování neřešte.
Například pro body [4,4], [2,3], [3,1], [0.5,1] a [4,1.5] na levém
obrázku takový obdélník nalezneme, pro body [0,2], [1,1], [4,1], [1,3], [3,4]
a [5,3] napravo ne.
Řešení
Výzkumníkům se sice povedlo zjistit, že je místnost jenom fázově posunutá a leží na
okraji otevřeného časového víru, ale v záchraně Willa se nedostali o nic dál.
Navíc skomírající generátor už dlouho časový vír pod kontrolou neudrží a nikdo
nevěděl, jak velké škody v čase by jeho vymknutí se kontrole mohlo způsobit.
Unikající chladící kapalina z generátoru tvořila stále silnější a silnější
ledový povlak na jedné z jeho částí a krystal dilithia v jádru byl nebezpečně
popraskaný. Na opravu by stačil jakýkoliv dostatečně velký dilithiový krystal,
problém tkvěl v tom, že k Willovi nemohli nic dostat. Ale jeden
z výzkumníků dostal skvělý nápad – Willovi tak skvělý nepřipadal – a to,
aby si Will obstaral potřebné věci v minulosti.
A tak se stalo, že se Will znovu postavil na plošinu ve středu generátoru,
zadoufal, že krystal tuhle jednu cestu ještě zvládne, a stiskl tlačítko ovládání
na své levé ruce.
* * *
Se zábleskem se zjevil na nějaké louce. Byla mu nepříjemná zima a netušil, kde
se ocitl. Kus vedle ale žongloval nějaký člověk s pochodněmi a Will se rozhodl,
že si nějakou vypůjčí. Vyhlédl si jednu opuštěnou a rozběhl se pro ni. Ale zrovna
v tu chvíli se chlapík otočil a začal ji brát do ruky. Will ho v rozeběhu
odstrčil, pochodeň popadl a nabral to směrem k nejbližšímu lesu.
Chlapík se za ním rozeběhl a byl asi lepší běžec než Will. Pomalu ho začal
dohánět, a tak Will za běhu hrábl po minipočítači na ruce. Skok časem dělat
nechtěl, ale několika místními přesuny by ho setřást mohl. Stejně je chtěl
použít k prozkoumání většího území.
 28-5-2 Místní přesuny (11 bodů)
28-5-2 Místní přesuny (11 bodů)
 S pomocí lokálního transportéru se může Will přemisťovat mezi libovolnými dvěma
body, které ho zajímají. Při průzkumu okolí by rád navštívil N bodů na mapě
nacházejících se v konvexní poloze – to jsou takové body, které můžeme všechny
umístit na obvod nějakého konvexního mnohoúhelníku, neboli napnout kolem nich
gumičku tak, aby všechny body obepínala zvenku.
S pomocí lokálního transportéru se může Will přemisťovat mezi libovolnými dvěma
body, které ho zajímají. Při průzkumu okolí by rád navštívil N bodů na mapě
nacházejících se v konvexní poloze – to jsou takové body, které můžeme všechny
umístit na obvod nějakého konvexního mnohoúhelníku, neboli napnout kolem nich
gumičku tak, aby všechny body obepínala zvenku.
Na přesun mezi dvěma body spotřebuje Will tolik energie, jak jsou body od sebe
na mapě daleko (počítáme vzdálenost vzdušnou čarou). Chtěl by začít v libovolném
bodě, navštívit všechny ostatní body a spotřebovat přitom co nejméně energie.
Vymyslete algoritmus, který mu pomůže najít výše popsanou cestu. Níže můžete
vidět ukázku bodů v konvexní poloze a nejlepší nalezené cesty mezi nimi (plná
čára značí cestu, čárkovaná napnutou gumičku).
Řešení
Po setřesení chlapíka udělal Will ještě pár skoků po okolí, než zaměřil svoji
časoprostorovou pozici, a posledním skokem se ocitl v nějakém divném sklepě.
„Dílna, skvělé!“ zamumlal si potichu a šel se podívat, jestli by se mu něco
nehodilo. Cestou si všiml divné klece v temném rohu, ale nevěnoval jí pozornost.
Našel kladívko, krásné nůžky na plech a chtěl už odcházet, když mu ale něco
nedalo, otočil se a pozorněji se podíval na klec. Uvnitř byl muž, k smrti
vystrašený muž!
Will vyskočil na nízkou klec, z náramkového počítače vytáhl žhavou krájecí jehlu
a začal zpracovávat mříže. Nakonec za ně trhl a vyrval je.
V tom zaslechl na schodech kroky a rozhodl se rychle zmizet. Otočil se k muži
v kleci, řekl jenom „Uteč!“ a sám se rychle vydal s pochodní v ruce ke
schodům, zadávaje přitom sekvenci k časovému přesunu na minipočítači.
Těsně, než došel ke dveřím, vyšel z nich druhý muž. Teď už se přesunu nedalo
zabránit a Will muži nechtěl ublížit, tak se ho pokusil odstrčit do bezpečné
vzdálenosti a vyběhnout z domu. V půlce schodů po něm muž natáhl ruku, ale
přesně v tu chvíli se obvody nabily a okolo Willa vyrostla modrá koule…
* * *
Objevil se v nějaké jeskyni, ale přesunem neprošel sám. Před něj dopadla na zem
zuhelnatělá lidská ruka. „Sakra!“ zaklel a pak si všiml, že v jeskyni je
ještě nějaký římský voják, potlučený, s potrhanou zbrojí a beze zbraně.
Potom ale jeho zájem přilákal geologický senzor za pasem, který se rozblikal.
V okolí se nachází velký dilithiový krystal, přesně to, co hledal! Začal obcházet
okolní zdi, než objevil pořádně velký kus. Ten s vítězoslavným rozmachem
kladívka vyloupl, sebral ho, hodil ještě jeden pohled po zkoprnělém Římanovi
a stiskem návratového tlačítka se přesunul zpět ke generátoru.
* * *
S pomocí pochodně rozmrazil zamrzlé potrubí, nůžkami na plech se mu povedlo
uvolnit vzpříčené kusy kovu nad nouzovým ventilem a tím pak zastavil únik
chladící kapaliny. Nakonec vyměnil krystal v jádru, ten původní už byl skoro
rozpadlý na prach, a spojil se interkomem s ostatními.
Willovo nadšení bylo ale vzápětí zchlazeno – zbytek týmu mezitím zjistil, co
způsobilo celou havárii: Klíčová část generátoru se sama přenesla do minulosti,
spálila svůj iridiový obal a vybuchla, což poničilo celý časoprostor. Se strojem
času se půjde přenést do okamžiku těsně předtím, než dojde k výbuchu, ale je
potřeba nové iridium k zastavení reakce.
* * *
A tak se stalo, že se Will ocitl v podzemí nějaké banky 20. století
před velkým sejfem, ve kterém měl být dostatečně velký kus čistého iridia
získaný po dopadu nějakého meteoritu. Jenže trezor měl dost propracovaný alarm.
 28-5-3 Trezor s alarmem (10 bodů)
28-5-3 Trezor s alarmem (10 bodů)
Alarm v trezoru je soustava různě propojených obvodů, kterými teče stejnosměrný
elektrický proud. Do jednoho místa soustavy je připojen záporný pól a od něj
teče proud elektronů různými cestami ke kladnému pólu připojenému také na jedno
místo v soustavě. Pokud se tok proudu přeruší, alarm vyhlásí poplach.
Jednotlivé dráty jsou pospojovány v uzlech a pro každý drát víme, kterým směrem
v něm teče proud. Opačným směrem téci nemůže a v zapojení nejsou žádné
orientované cykly.
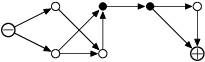
Zapojení alarmu může vypadat jako na obrázku níže. Najděte
ve schématu zapojení všechny uzly, kterých se za žádných okolností nesmíme
dotknout (neboli takové, jejichž přerušení by přerušilo všechny cesty od
záporného ke kladnému pólu). V příkladu níže jsou takové uzly vyznačeny černě.
Řešení
Willovi se povedlo alarm rychle obejít, byla to celkem zastaralá technologie,
i když na svoji dobu docela špička. V trezoru nikým nepozorován vzal trezorovou
schránku, kde podle jeho záznamů mělo být iridium, otevřel ji a vyndal kus
našedlého kovu. Pak ho schoval do kapsy kombinézy, schránku zase vrátil na
místo a vyšel z trezoru ven.
Než se dostal do dvorany banky, zjistil, že je banka přepadena. No aspoň to
lupiči budou mít o něco lehčí, řekl si při pomyšlení na odblokovaný trezor
a vyřazený alarm v něm. Ale to už sahal znovu po svém minipočítači a skočil
časem i s iridiem v kapse dříve, než si toho mohl kdokoliv všimnout.
* * *
Tentokrát se Will zjevil v nějakém skladu plném zásob jídla a s hrozným lomozem
přitom shodil několik polic. Narazil si u toho nohu a zaklel: „Co to sakra?
Vždyť jsem se měl vrátit zpátky!“
Teď o tom ovšem nebyl čas přemýšlet dál. Dveře do skladu byly vzpříčené, ale
vykopnutí je otevřelo a jemu se naskytl pohled na kuchyň. Současně s tím jeho
minipočítač zapípal, když v místnosti zdetekoval podivný časový vír. Jakoby
vycházel z pánve visící na zdi. „Tohle si vezmu,“ zamumlal a pánev sundal
z hřebíku.
Nějaký kuchař se mu pokusil pánev vytrhnout z ruky, ale Will ho odstrčil a se
slovy „Na tohle nemám čas,“ vyběhl na ulici a zmizel v temné boční uličce.
Tam začal zkoumat, proč ho pánev přitáhla na tohle místo.
Zmapoval, že mimo pánev existuje ještě několik dalších časových vírů, které se
asi při výbuchu časového generátoru náhodně rozmístily po časoprostoru a tvoří
teď jakési časoprostorové mosty. Willa by zajímalo, co se bude při jejich
odstraňování s časoprostorem dít.
 28-5-4 Časoprostorové mosty (10 bodů)
28-5-4 Časoprostorové mosty (10 bodů)
Will zjistil, že různé časy a místa jsou náhodně svázány časoprostorovými mosty.
Každé místo v sobě nese jistý náboj energie a na počátku jsou všechna spojena
tak, že tvoří souvislý graf.
Will si vymyslel pořadí, v jakém chce časoprostorové mosty odstraňovat, což
povede k tomu, že se původně souvislý graf bude rozpojovat na menší a menší souvislé
komponenty. Potřeboval by zjistit, jak se bude množství energie v jednotlivých
komponentách chovat vzhledem k odstraňování mostů – vždy nás bude zajímat
součet energie v rámci jednotlivých komponent.
Dostanete zadáno, kolik energie je v každém místě, a pak pořadí
časoprostorových mostů, ve kterém je chce Will odstraňovat. Po každé operaci
byste měli vypsat, co se stalo – buď nic (operace nerozpojila žádné dvě
komponenty), nebo že došlo k rozpojení komponenty na dvě s takovou a takovou
energií.
Příklad: Pokud budeme mít místa A, B, C a D s energiemi po řadě
1, 2, 3 a 4 a tato místa budou spojená do čtverce ABCD, tak následující
posloupnost operací provede toto:
- Zrušení A-D: Nic.
- Zrušení B-C: Rozpojení na 2 části s energiemi 3 a 7.
- Zrušení A-B: Rozpojení na 2 části s energiemi 1 a 2.
- Zrušení C-D: Rozpojení na 2 části s energiemi 3 a 4.
Řešení
Po naplánování ideálního pořadí rušení časoprostorových mostů přišla řada na
realizaci. Will pečlivě navolil, na jaké místo a čas se chce dostat, spustil
přesun…
* * *
…a ocitl se na místě, kde určitě nechtěl být, v nějakém římském stanu.
Potřásl hlavou a rozsvítil si svítilnu na ruce. Všiml si na posteli ležícího
překvapeného Římana. Náramně se podobal tomu, kterého potkal v jeskyni. Teď se
začal zvedat, a tak si Will přiložil prst na ústa v pradávném gestu pro mlčení.
Pak si všiml vybaveného stolu s množstvím kladiv, kleští a dalších věcí. Rozhodl
se, že si pánev trochu vylepší, urazil z ní držadlo a chvíli ji upravoval, aby
ji později mohl použít k rozdrcení iridia na menší kusy. Pak si sbalil věci
a chystal se k odchodu, tentokrát jen aby udělal místní přesun.
Ale ještě než zmizel, ohlédl se po Římanovi. Ujistil se, že je to ten
z jeskyně, z věšáku vedle jeho postele popadl zbroj, štít a zbraň a přesunul
se.
Přesun to nebyl daleký, chtěl jenom vypátrat, jak hluboko v minulosti se ocitl
a jak by měl nakalibrovat svůj minipočítač, aby už dělal časové přesuny přesně.
 28-5-5 Kalibrace (7 bodů)
28-5-5 Kalibrace (7 bodů)
Willův minipočítač má v paměti uložen seznam časoprostorových souřadnic
uspořádaných původně podle času. Ale vypadá to, že se vlivem nějaké poruchy
seznam o něco zrotoval, a Will by rád zjistil, o kolik pozic.
Víme, že všechny časy jsou navzájem různé a že mimo zrotování se nic jiného
nestalo. Z původní posloupnosti
1,3,4,7,9,12,13,14,15
tak mohla vzniknout třeba tato (zrotováním doprava o tři):
13,14,15,1,3,4,7,9,12
Bohužel jediné, co může Will dělat, je podívat se na nějaký index
v posloupnosti, přesunout se časem na tyto souřadnice a určit, jakému odpovídají
času. Rád by zjistil, o kolik se posloupnost souřadnic přesně zrotovala, ale
chce při tom vykonat co možná nejméně cest časem (neboli podívat se na co nejméně
pozic v seznamu). Vaším úkolem je navrhnout mu nejlepší postup, tedy postup
s řádově co nejméně nutnými přesuny časem.
Řešení
Po provedení několika pokusů, při kterých se zjevil s mečem v ruce před nějakým
domem, pak ve sklepě Bílého domu a nakonec v Disneylandu, se Willovi konečně
povedlo nakalibrovat správně minipočítač.
Teď už mohl přesně zaměřit místo a čas, kde mělo dojít k výbuchu části časového
generátoru, která se přenesla do minulosti. Nastavil s velkou přesností stejné
místo a čas o pět minut předtím. Iridium pomocí kladívka a pánve přeměnil na
drobnější kousky, které plánoval nacpat do jádra, aby zastavil reakci. A potom
zmáčkl tlačítko.
* * *
Objevil se v docela běžném panelákovém obývacím pokoji. Tedy byl by běžný, kdyby
v půlce zdi nevisel podivný třímetrový kovový válec, který se materializoval
uprostřed železobetonového panelu, jedním koncem v televizi. Válec vydával
hluboký pulzující zvuk, který se začal zrychlovat. Will odklopil kryt na boku
a doslova ho srazilo na zem teplo, které se vyvalilo ven. Bylo tak veliké, že
skoro okamžitě chytly plamenem blízké záclony.
Will si zastínil obličej rukou a přiblížil se k válci. Po otevření krytu se ven
vysunuly regulační sloty, do kterých by se mělo umístit iridium, ale nevysunuly
se všechny (a Will stejně neměl tolik kousků iridia, aby je umístil do všech).
 28-5-6 Sloty na iridium (11 bodů)
28-5-6 Sloty na iridium (11 bodů)
Máme k dispozici K kousků iridia a S slotů, do kterých se dá iridium
umístit. Slotů je alespoň tolik, kolik je iridia (K≤ S), ale nejsou
rozmístěny rovnoměrně. Všechny sice leží na obvodu kruhu, ale jsou různě daleko
od sebe.
Iridium do nich potřebujeme rozmístit co možná nejvíce rovnoměrně. Za co nejvíce
rovnoměrné rozmístění budeme považovat takové, které umístí každý kousek iridia do
jiného slotu a obsazené sloty budou co nejdále od sebe – minimum ze vzdáleností
mezi obsazenými sloty bude největší možné. Vzdálenost počítáme po obvodu kruhu
(a to i přes začátek kruhu).
Sloty mají celočíselné souřadnice (mohly by to být třeba stupně) a naším úkolem je
z nich rychle vybrat ty, které použijeme. Pokud bude možných několik stejně
výhodných kombinací, můžeme použít libovolnou z nich.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku vstupu budou tři čísla: obvod kruhu O,
počet slotů S a počet kousků iridia k umístění K. Na druhém řádku vstupu
pak bude S celých čísel si označujících pozice slotů na kruhu z rozsahu
0≤ si < O. Všechna čísla budou oddělená mezerami a pozice budou seřazené od
nejmenší.
Formát výstupu: Na jediný řádek výstupu vypište K mezerou oddělených
indexů označujících sloty, které budou použité. Indexujeme od 0.
Ukázkový vstup:
36 10 4
0 2 4 8 12 20 22 24 30 35
Ukázkový vstup a výstup si můžeme přiblížit obrázkem níže. Použité sloty jsou
označeny plným puntíkem, minimální vzdálenosti mezi použitými sloty je 8 a větší
vzdálenosti dosáhnout nelze.
Řešení
Co nejrychleji vložil kousky iridia do slotů a udeřil do oranžového tlačítka.
Sloty se zasunuly a Will sebou pro jistotu praštil o zem. Uvnitř došlo k bouřlivé
reakci a ven vylétly rozžhavené jiskry, které zapálily blízké okolí. Ještě že
kombinézy fasované v institutu byly nehořlavé! Po pár sekundách ale začala
reakce ustávat, iridium zafungovalo jako regulátor.
Will se uprostřed hořícího bytu postavil, podíval se na nyní už neškodný válec
a aktivoval v něm malou autodestrukční nálož. Pak s modrým zablesknutím
z hořícího bytu rychle zmizel, dole už totiž zaslechl houkání sirén.
* * *
Z modré koule se vyloupl opět v místnosti s reaktorem, teď navíc s krátkým
efektem šlehajících plamenů, které vtáhl s sebou. Ušklíbl se nad tím a spojil se
s ostatními.
„Tak časové havárii jsme snad zabránili, zamezil jsem výbuchu!“ oznámil.
„Skvěle, tak teď tě už jenom dostat zpátky,“ přišla mu odpověď.
Aby vrátili místnost s reaktorem (a Willem) zpátky do normální fáze, museli
omezit vzniklý časový vír. K tomu ale bylo potřeba provést velmi mnoho rychlých
časoprostorových výpočtů v krátkém čase – když už se operace zahájí, nejde
přerušit ani pozastavit. Proto se rozhodli si něco předpočítat předem.
 28-5-7 Tajemná operace (12 bodů)
28-5-7 Tajemná operace (12 bodů)
Máme počítač počítající tajemnou operaci ⊗, o které víme jenom to, že je
binární a asociativní (tedy že je to operace mezi dvěma prvky a že nezáleží na
uzávorkování operací ve výrazu). Co si pod tím představit? Může to být například
obyčejné násobení nebo sčítání, nebo třeba násobení modulo 109 (všimněte si,
že na rozdíl od běžného násobení k tomuto neexistuje inverzní operace – není
tedy možné dělit).
Běh programu se bude skládat ze dvou částí. V první části si může program
v nějakém rozumném čase předpočítat, co bude chtít, a pak bude ve druhé (ostré)
části běhu dostávat dotazy. Problémem je, že výpočet tajemné operace ⊗
je náročný a během ostrého běhu zvládne počítač v čase každého dotazu
použít operaci ⊗ pouze jedenkrát.
Na začátku běhu dostane program pevně daná čísla a1 až an, na nichž si
můžeme spočítat, co bude chtít, a při ostrém běhu pak bude dostávat mnoho
dotazů typu
ai ⊗ai+1 ⊗…⊗aj-1 ⊗aj
neboli dotazů na výpočet operace ⊗ na nějakém intervalu mezi i a j
(kde i≤ j).
Chtěli bychom si tedy vybudovat nějakou datovou strukturu, která nám při
ostrém běhu umožní odpovídat na takové dotazy pouze s jedním zavoláním funkce
⊗. Ale výpočet takové struktury by taky měl být co možná nejrychlejší.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Výpočty byly dokončeny, místnost s generátorem vrácena do správné fáze a Will už
se chystal k tomu, že si po náročném dni půjde dát horkou sprchu. V tom jeho
pohled padl na římské brnění a meč, které přinesl a položil s otlučenou pánví do
kouta. Chvilku přemýšlel, pak to vše vzal do náruče a do interkomu oznámil:
„Ještě moment, mám nějakou nevyřízenou práci…“
* * *
Než se Gaius stihl vzpamatovat a pořádně nadechnout, zablesklo se podruhé
a cizinec se vrátil. Teď tam však místo pochodně stál s pánví v jedné ruce
a centurionskou zbrojí ve druhé. Řekl něco dalšího nesrozumitelného a hodil
zbroj i s mečem Gaiovi k nohám. Pak ho rukou pobídl, aby se do ní navlékl.
Gaius dlouze neváhal a cizince poslechl. Jakmile na sebe zbroj navěsil, podíval
se na cizince, co teď. Ten se nahnul, hodil něco nalevo do lesa, na prstech
odpočítal od tří do jedné a silně strčil Gaia do zad. Ten vyběhl současně s tím,
co se zleva z lesa začaly ozývat divné zvuky…
Příběh pro vás dovyprávěl
Jirka Setnička
 28-5-8 Neuronové sítě (14 bodů)
28-5-8 Neuronové sítě (14 bodů)
V minulém dílu seriálu jsme se zabývali modelem biologického neuronu –
perceptronem. Ukázali jsme si, jak takový model „naučit“ a použít
k jednoduché klasifikaci, tedy roztřídění vstupů do několika skupin. V zadané
úloze jste nakonec bojovali s tím, že jeden perceptron dokáže klasifikovat jen
do dvou skupin.
Dnes se podíváme na struktury z umělých neuronů složené, neuronové sítě,
jejichž schopnosti jsou mnohem širší. Používají se k obecné klasifikaci,
rozpoznávání zapamatovaných vzorů, organizaci dat do skupin podle podobnosti
nebo třeba k řešení optimalizačních úloh.
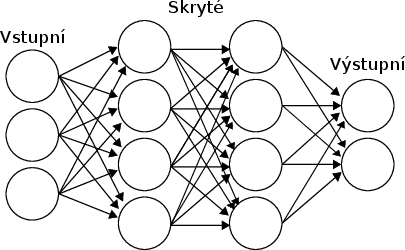
Dopředné vrstevnaté neuronové sítě
Nejoblíbenější způsob, jak zapojit neurony do sítě, je rozdělit je do vrstev
1,2,...,N. Mezi vrstvami napojíme výstup každého neuronu z vrstvy k na
vstup každého neuronu z vrstvy k+1. Každý z těchto vstupů má svoji váhu a
každý z neuronů má svůj práh – stejně jako u jednoduchého perceptronu.
První
vrstvě říkáme vstupní. Je trochu speciální, protože nepřijímá signály od
jiných neuronů, ale přímo vstupní data a ta bez úpravy předává dál. Podobně
poslední vrstva se nazývá výstupní, protože z ní čteme výstup sítě.
Ostatní vrstvy jsou pro okolní svět skryté.
Tuto neuronovou síť bychom teď rádi naučili něco užitečného, tedy našli nastavení
vah, které by zajistilo, že pro vstupy z trénovacích dat bude výstup sítě co
nejpodobnější požadovanému výstupu. Tuto podobnost měříme pomocí chybové funkce
neuronové sítě:
Kde yj,i je výstup j-tého neuronu při i-tém vstupu sítě a dj,i je
požadovaný výstup ve stejném případě. Na předpisu této funkce je zajímavé, že
chyba (nebo také odchylka) každého neuronu je umocněna na druhou, aby se
zdůraznily velké chyby a zanedbaly malé. Sumy pak sečtou chyby ze všech neuronů
pro všechna trénovací data. Polovina je v tomto vztahu jen proto, aby lépe vyšla
jeho derivace – to zde ale dělat nebudeme.
Aby učící algoritmus mohl postupně snižovat chybu úpravou váhy neuronů, hodilo
by se nám, aby aktivační funkce neuronu postupně a spojitě rostla s rostoucím
potenciálem neuronu. Místo skokové funkce signum z minulého dílu tedy v našem
seriálu použijeme sigmoidu:
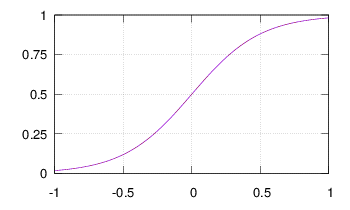
λ je v této funkci konstanta, jejíž nastavením můžeme měnit strmost
funkce. K jejímu vlivu na učení se ještě dostaneme. Písmenkem ξ (ksí) značíme potenciál, e možná už znáte jako Eulerovo číslo.
Níže můžete vidět průběh sigmoidy pro λ= 4:
Výpočet výstupu sítě
Algoritmus pro výpočet výstupu sítě vychází přímo ze vztahů platících pro
perceptron. Postupně počítá výstupy jednotlivých vrstev počínaje první skrytou
(která vstupní vrstva data nijak nezpracovává). K výpočtu potenciálu ξj
podle výstupů předchozí j-té vrstvy používá vztah z minulého dílu:
ξj = ∑i yi wij. Potenciál se
pak dosadí do aktivační funkce, v našem případě sigmoidy.
Nikoho, kdo četl
předchozí díl, by teď nemělo překvapit, že zvlášť nepočítáme s prahem (anglicky
bias). Ten je totiž schovaný v přidaném neuronu s konstantní hodnotou
-1, ze kterého vede vstupní hrana s váhou odpovídající velikosti prahu.
Pro implementaci se může hodit si všimnout, že výpočet potenciálu je skalární
součin dvou vektorů. Pokud váš programovací jazyk tedy vektory (v matematickém
smyslu) a operace s nimi podporuje, můžete si jejich použitím občas ušetřit
trochu práce. Kromě toho můžete zjednodušením kódu ušetřit práci i
čtenáři, což je v programování často ještě důležitější princip.
Úkol 1 [2b]
Vymyslete neuronovou síť modelující logickou funkci XOR. Síť bude mít dva
vstupy a jeden výstup. Počet vrstev a skrytých neuronů je na vás, ale snažte se
o minimalitu. Pošlete nám kresbu sítě včetně vah a vysvětlení, proč je
vaše síť nejmenší možná.
Zpětná propagace
K učení, tedy minimalizaci chybové funkce E, se používá mnoho různých
algoritmů. My se podíváme na nejzákladnější z nich, zpětnou propagaci.
Nejdříve si popíšeme její myšlenku.
Na počátku náhodně nastavíme všechny váhy.
Učení pak probíhá tak, že náhodně vybíráme z trénovacích dat, pro každý vstup
necháme síť vypočíst výstup a porovnáme ho s požadovaným výstupem z trénovacích
dat. Na základě tohoto porovnání upravíme váhy sítě tak, aby se snížila chyba
sítě – výstup se přiblížil k požadovanému.
Postupně procházíme vrstvami od výstupní k vstupní a upravujeme váhy každé
vrstvy tak, abychom snížili chybu té následující směrem k výstupní.
Převést tuto myšlenku do řeči matematiky vyžaduje trochu matematické analýzy,
takže na to pro účely seriálu půjdeme trochu od lesa. Nejdříve vám ukážeme
vzorce, které zpětná propagace na úpravu vah používá, a poté trochu objasníme
jejich části.
Chceme určit novou váhu wij(t+1) spoje z neuronu i do neuronu
j v kroku t+1. Změna této váhy bude záviset na chybě neuronu j a výstupu
neuronu i:
wij(t+1) = wij(t) + αδj yi
kde δj je chyba neuronu j. Ta se dá přímo spočítat pro výstupní
vrstvu:
δj = (dj - yj) λyj(1-yj)
Pro skryté vrstvy je ale třeba ji odvodit na základě chyby, kterou už máme
spočítanou pro sousední vrstvu směrem k výstupní:
δj = (∑k δk wjk )λyj (1-yj)
Kdy učení skončit a prohlásit síť za naučenou nebo naopak nepoučitelnou? Jedna
z možností je sledovat chybu sítě. Pokud se průměrná chyba testovacích výstupů
dlouho nesnižuje, lepší už to asi nebude.
Lepší možnost je vyzkoušet síť na
vstupy, které v trénovacích datech nejsou. Takovým vstupům se říká testovací
data, protože na nich testujeme naučenost sítě. Proč je lepší oddělit testovací
a trénovací data? Představte si, že chcete neuronovou síť naučit třeba
rozpoznat sudá od lichých čísel.
I pokud síť rozpozná naše trénovací čísla bez
chyby, je možné, že se naučila jen seznam všech sudých nebo lichých čísel a
jiná čísla může dál rozpoznávat špatně. Takovému stavu, kdy se síť příliš
zaměřila na trénovací data, se říká přeučení. Naopak schopnosti sítě
zobecnit řešení říkáme generalizace. Díky testovacím datům umíme tyto dva
jevy rozlišit.
Pokud nám neuronová síť dává dobré výsledky na trénovacích i testovacích
datech, znamená to že bude mít takto malou chybu i na dalších vstupech? Ani to
ne! Učení totiž zastavujeme právě tehdy, když budou tyto chyby malé. Pokud
chceme odhadnout chybu, se kterou bude síť pracovat pro další data, je dobré ji
znovu změřit pro oddělenou sadu dat, validační data.
Uff, dat už
potřebujeme pěknou hromádku, kde je ale vzít? To je společně s výpočetní
náročností jednou z největších výzev strojového učení. Stroje svoji neobratnost
v učení kompenzují velkým množstvím trénovacích dat. Zatímco dítěti stačí vidět
pár čísel, aby se naučilo rozlišovat sudá a lichá, stroje jich potřebují řádově
víc.
Mnoho současných technologických společností je schopno vytvářet
„inteligentní“ řešení právě díky tomu, že mají od uživatelů svých služeb
sesbíráno obrovské množství dat. Nám budou muset stačit veřejné datasety
dostupné na internetu. Jak je rozdělit na trénovací, testovací a validační
část? Náhodně; přičemž většina se obvykle používá na trénování.
Předzpracování dat
Narozdíl od perceptronů, neuronové sítě obvykle pracují s čísly v rozsahu
[0;1], a i naše aktivační funkce má obor hodnot v tomto rozsahu. To pro nás
znamená, že bychom si data pro neuronovou síť měli předzpracovat, aby byly
v tomto rozsahu. Těmto technikám předzpracování se říká normalizace a
my ji budeme provádět stejně jako v minulém díle seriálu.
Pokud například chceme,
aby neuronová síť pracovala s výškami dospělého člověka, které se v našich
datech pohybují od 140 po 200 cm, přepočítáme tyto výšky tak, aby
140 odpovídalo nule, 200 odpovídalo jedné a vzájemné poměry výšek zůstaly stejné.
Pokud síť používáme ke klasifikaci do k skupin, často můžeme dosáhnout
lepších výsledků, když místo jednoho výstupu sítě, který by udával číslo
skupiny 1,..,k, použijeme k výstupních neuronů. i-tá skupina se pak
reprezentuje tak, že i-tý neuron má hodnotu 1 a ostatní 0 (nebo v blízkosti
těchto hodnot).
Počáteční parametry
Chování zpětné propagace ovlivňuje několik parametrů a
způsob generování počátečních vah.
Parametry mají vliv hlavně na rychlost učení. Pokud učení
nastavíte příliš rychlé, může algoritmus úplně ztratit schopnost chybu sítě
zlepšovat a učení nebude fungovat. Konkrétní volba parametrů závisí na řešeném
problému a často se s ní experimentuje.
Parametr
λ nastavuje strmost aktivační funkce, v našem případě
f(ξ)
= . Jak si můžete sami vyzkoušet dosazováním,
větší
λ znamená strmější funkci. Strmá funkce pak zrychluje učení,
protože menší potenciál (a tedy menší rozdíl vah) stačí k tomu, aby neuron
vydal výstup blízko
±1. Učení tedy pro velkou
λ nemusí váhy měnit
o tolik, což jej zrychlí.
Parametr α nastavuje rychlost změny vah
v každém kroku učení. Jak je vidět ve vztahu pro aktualizaci vah: wij(t+1) =
wij(t) + αδj yi, větší α způsobí větší změny vah.
Obvykle používáme λ∈[0.5;4] a α∈[0.2;1].
Zbývá vyřešit volbu počátečních vah. Ty bychom chtěli nastavit tak, aby
průměrný neuron reagoval na vstupy v rozsahu [0;1] opět potenciálem v rozsahu
[0;1].
Nechceme tedy například, aby neurony s většími počty vstupů generovaly
potenciály (v absolutní hodnotě) mimo zmíněný rozsah. Proto by takové neurony
měly mít menší váhy svých vstupů. Doporučujeme volit počáteční váhy
v rozsahu
±, kde
N je počet vstupů neuronu.
K přesnému odvození tohoto vztahu je potřeba smíchat trochu matematické
statistiky a integrálního počtu, takže jej zde zatajíme.
Úkol 2 [8b]
Podívejme se znovu na dataset o kosatcích ze
stránky seriálu. Zkusme
klasifikovat kosatce pomocí neuronové sítě a porovnat přesnost s řešením pomocí
perceptronů. Nezapomeňte na předzpracování dat. Původní autorské řešení, které
mělo z 60 trénovacích vzorů na zbytku datasetu 93.42 % přesnost, byste
měli bez problémů překonat.
Zkuste si pohrát s architekturou sítě (počtem
neuronů a vrstev) a parametry a do řešení připište, na co jste přišli.
V odevzdaném řešení rozdělte dataset v poměru 50:25:25 % pro trénovací,
testovací a validační část.
Pokud jste úlohu z minulé série řešili, stáhněte si prosím dataset znovu,
opravili jsme v něm dvě drobné chyby. Od minula také připomínáme, že každý
řádek datasetu reprezentuje vlastnosti jednoho kosatce.
První řádek popisuje
význam sloupečků: první dva jsou délky a šířky kališních lístků, další dva jsou
délky a šířky okvětních lístků. Máme za úkol předpovědět poslední sloupec –
konkrétní druh kosatce: setosa, versicolor, nebo virginica.
Úkol 3 [4b]
Nakonec se podíváme na úlohu, která je pro náš „umělý mozek“ těžká:
rozpoznání srdce. Mějme neuronovou sít se dvěma vstupy, jednou skrytou
vrstvou s N neurony a jedním výstupem.
Síť bude na vstupu přijímat souřadnice
x a y bodu v rovině a její výstup se bude blížit 1, pokud bod leží uvnitř
srdce, a 0 v opačném případě. Srdce budeme pro naše účely znázorňovat známým
piktogramem tvořeným čtvercem a dvěma půlkružnicemi umístěnými nad jeho dvěma
sousedními stranami.
Zvolte si počet skrytých neuronů N (alespoň 6) a najděte nastavení vah této
sítě. Rozměry a souřadnice srdce si zvolte libovolně. Úlohu můžete vyřešit jak
pomocí zpětné propagace, tak pomocí tužky a papíru.
Jan Škoda
Řešení
 28-5-1 Zaměřování místnosti (9 bodů)
28-5-1 Zaměřování místnosti (9 bodů)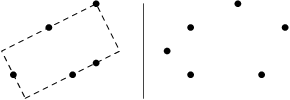
 S pomocí lokálního transportéru se může Will přemisťovat mezi libovolnými dvěma
body, které ho zajímají. Při průzkumu okolí by rád navštívil
S pomocí lokálního transportéru se může Will přemisťovat mezi libovolnými dvěma
body, které ho zajímají. Při průzkumu okolí by rád navštívil 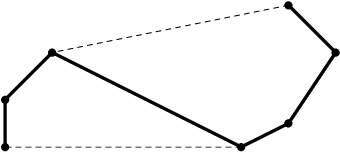

 28-5-6 Sloty na iridium (11 bodů)
28-5-6 Sloty na iridium (11 bodů)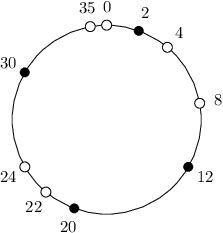
 28-5-7 Tajemná operace (12 bodů)
28-5-7 Tajemná operace (12 bodů) 28-5-8 Neuronové sítě (14 bodů)
28-5-8 Neuronové sítě (14 bodů)