Třetí série třicátého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu si vyslouží každý, kdo vyřeší alespoň 4 úlohy na alespoň polovinu bodů.
Zadání úloh
Zkouškové na Matfyzu? Ne, že by to byla taková hrůza, spíš nezávidím svému
trávicímu systému. Zítra mám zkoušku v devět hodin ráno (ráno, snad jste
si na matfyzácké pojetí času už zvykli) a kromě obědů v menze jsem zbytek
svého stravování řešil bagetami. Ono je to tak hrozně praktické, koupíte je na
vrátnici kolejí, je na ně studentská sleva a nemusíte nic vařit. Ale určitě
bych na kombinaci sýrových a šunkových baget nechtěl přežít celé zkouškové,
i když prý jsou někteří přeživší, kterým se to povedlo.
Venku se už setmělo a je čas na večeři. V kuchyňce si otevřu ledničku, sáhnu
po bagetě a chci se vrátit zpátky do pokoje, když vtom se to stane.
Najednou se mi zatočí hlava a před očima se mi udělají mžitky. Chci se chytit
dveří, abych nespadl, ale místo toho mávnu rukou do prázdna. Chvíli jsem úplně
zmatený a bezmocný. To se mi určitě z těch pitomých baget udělalo špatně…
Pak ucítím, jak ležím na pevné zemi. Nejdřív si myslím, že jsem prostě omdlel.
Jenže pak zaslechnu divné zvuky, které na matfyzácké koleje moc nepatří.
Nejdřív ucítím silný vítr s podivnou vůní. Pak zaslechnu šumění vln, které
naráží na… pobřeží? Otevřu oči. Moje nezdravá strava mi zřejmě musela
způsobit nějaké divné halucinace. Jinak si nedovedu vysvětlit, proč teď ležím
na písečné pláži a přede mnou je širé moře.
Ať tohle přestane! Než se zase vrátím do normálu, sednu si a budu počítat
přicházející vlny, abych se trochu uklidnil.
 30-3-1 Vlnění (9 bodů)
30-3-1 Vlnění (9 bodů)
Uvažujte čtvercovou síť představující vodní plochu. Z levého spodního pole se
do ostatních polí šíří střídavě bílé a černé vlny. Podívejte se na obrázek,
kde tečky jsou části bílých vln a dvojité mřížky jsou části černých vln:
####
...#
##.#
.#.#
Čtvercová síť má v levém spodním poli počátek a směrem doprava a nahoru je nekonečná
(obrázek představuje jen malý výřez). Vaším úkolem je zjistit počet čtverců, které
představují černé vlny, v zadané obdélníkové oblasti sítě.
Program dostane na vstupu souřadnice levého spodního rohu a horního pravého
rohu obdélníku, vždy nejprve číslo sloupce a poté číslo řádku. Číslujeme od
nuly a počátek je pochopitelně ve spodním levém poli. Protože zadaný obdélník
může být potenciálně rozsáhlý, chceme znát hodnotu výstupu modulo 1000000007
(tedy zbytek po dělení výsledku tímto číslem).
Řešení
Z počítání vln mě vytrhne nějaký hlas. „Ty jsi org KSPčka?“
„Ano, to jsem já.“ „Vítám tě v Japonsku. Jestlipak víš, kdo jsem?“
Pozoruji člověka, který se tu právě objevil. Má úplně plešatou hlavu. Říká, že
tohle je Japonsko, že by to byl nějaký zenový mnich? Ale pak si prohlédnu jeho
oči a dojde mi to. Je to pan Nápověda! Musel si ostříhat vlasy a celkově změnit
svoji vizáž, jinak bych ho hned poznal.
„Podle tvého výrazu usuzuji, že už to chápeš. Jsme v Japonsku a všichni
Japonci jsou takoví mírní a úslužní, takže tady nechci žádnou zbytečnou
potyčku. Stačí, abych ti ukázal, že nemáš šanci utéct.“
Instinktivně se chci otočit a zahájit úprk (i když je otázkou kam), ale
s hrůzou zjistím, že to nejde. Vůbec se nemůžu pohnout, ani nohama, ani rukama,
nijak! Jako kdybych vězel v nějaké svěrací kazajce. V Nápovědově ruce se objeví
drobná černá krabička.
„Tohle se mi tady podařilo sehnat. Dokáže to na docela velkou dálku zmrazit
pohyby jakéhokoliv člověka. Dýchat ti to dovolí, ale nic dalšího. Umí to
zmrazit i víc lidí najednou.“
 30-3-2 Zmrazovač (10 bodů)
30-3-2 Zmrazovač (10 bodů)
Pan Nápověda pověřil dva ze svých agentů, aby znehybnili co nejvíce nepřátel.
Nepřátelé stojí na rovné cestě o celkové délce K a pro každého z nepřátel
znáte jeho pozici P, 0 ≤ P ≤ K, P ∈N. Každý z agentů má k dispozici
znehybňovací zařízení, které zmrazí jakéhokoliv nepřítele, jehož vzdálenost
k agentovi je menší nebo rovna X.
Máte zadané parametry K, X a pozici každého nepřítele s tím, že nepřátelé
jsou už na vstupu seřazeni podle své pozice. Najděte dvě celočíselné pozice na cestě,
kam si mohou stoupnout agenti, aby znehybnili co největší množství
nepřátel.
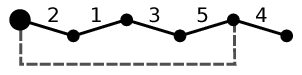
Příklad ukazuje úlohu s K = 14 a X = 2. Dokážeme zmrazit všechny nepřátele,
pokud umístíme agenty na polohy 6 a 10 (vyznačené trojúhelníčkem).
Pro jistotu ještě opakujeme: pozice nepřátel i agentů jsou celočíselné.
Řešení
„Ale jak jsem se sem, do háje, dostal?“ ptám se. Nápověda se zasměje. „Že
sis vzal něco na památku z mého bunkru?“ „No, zkoumali jsme nějaké věci,
které se tam našly. Já si vzal na kolej takové divné těžítko, chtěl jsem to, až
skončí zkouškové, rozebrat…“
„To tvoje těžítko byl experimentální teleportér,“ vysvětlí mi. „Asi
se nějakým omylem zapnul. Můžeš být vlastně rád, že jsi naživu a že tě to
neposlalo třeba na zemskou oběžnou dráhu – někteří zvědavci, kteří to zkoušeli,
skončili takhle ošklivě. Poslední firmware, který se tam nahrál, teleportoval
lidi do blízkosti mé osoby, proto jsi skončil tady. Kdyby to zařízení bylo
trochu přesnější a spolehlivější, hodně by mi to ušetřilo přesuny.“
 30-3-3 Teleportér (9 bodů)
30-3-3 Teleportér (9 bodů)
Pan Nápověda kdysi vybudoval řadu N tajných základen. Ty jsou očíslované
a platí, že jediná cesta z i-té do (i+1)-té základny vede tunelem o délce
Di, což je kladné číslo. Pro cestu mezi dvěma vzdálenějšími základnami je
tedy nutné projít všechny tunely mezi nimi. Hlavní sídlo pana Nápovědy se
nachází v první základně a uvažujeme veličinu Mi jako délku nejkratší cesty
z i-té do první základny.
Spočtení Mi je při tomto zadání triviální (prostě sečteme délky všech tunelů
mezi základnami). Výzkumnému týmu se však podařilo vyrobit teleportér. Chtějí
vybrat dvě základny, mezi kterými bude možnost okamžitého přesunu – jako
bychom mezi ně přidali nový tunel s délkou 0. Při cestách mezi jinými
základnami je samozřejmě na část cesty možné teleport využít také.
Pan Nápověda chce umístit teleportér takovým způsobem, aby se co nejvíce
zrychlila cesta do první základny. Vyberte, do jakých dvou základen umístit
teleportér, aby maximum všech Mi (pro všechny základny) bylo co nejmenší.
Pozor, zvláště v této úloze chceme důkaz správnosti vašeho řešení.
Na obrázku vidíte zadání úlohy s jediným správným řešením – nejdelší cesta
vede z vrcholu mezi tunely délky 3 a 5, kdy musíme projít tunelem délky 5
a potom teleportérem.
Řešení
Nápověda si otráveně povzdychne, jako by ten rozhovor trval až moc dlouho.
„Když jste zničili můj bunkr, přišel jsem o všechno. Pomocí jednoho
teleportéru jsem se přenesl do Tokia, kde jsem měl aspoň nějaké kontakty. Nic
z mých vynálezů se ale nezachovalo. Zmohl jsem se na útok s tím počítačovým
virem, ale jinak musím celé své impérium vybudovat znovu… Proč ti to
vlastně říkám? Taky nemusíš vědět všechno,“ usměje se. Znovu vytáhne
znehybňovací krabičku, stiskne na ní tlačítko a já omdlím, tentokrát opravdově.
* * *
Když přijdu k sobě, jsem v nějaké temné kobce, jen spoře osvětlené
poblikávající zářivkou. Začínám mít dojem, že tu zítřejší zkoušku nestihnu.
Jsou tady dveře, ale samozřejmě zamčené. V rohu místnosti se nachází stůl,
židle a na stole zapnutý notebook. Na displeji se postupně zobrazují červené
a zelené tečky. V rohu svítí nápisy: hmota a antihmota. Pak začne
blikat jiný nápis: odděl je! Tak si sednu a začnu to řešit. Nemůžu si
pomoci, skoro to vypadá, že mě Nápověda přihlásil do nějaké programátorské
soutěže.
 30-3-4 Hmota a antihmota (12 bodů)
30-3-4 Hmota a antihmota (12 bodů)
 Jednomu z pracovních týmů pana Nápovědy se podařilo najít způsob, jak od sebe
oddělit částice hmoty a antihmoty. Protože se ale stále jedná o experiment,
potřebovali by ověřit, zda jsou od sebe odděleny skutečně dokonale. Pro jednoduchost
budeme uvažovat jen částice ve dvourozměrném prostoru.
Jednomu z pracovních týmů pana Nápovědy se podařilo najít způsob, jak od sebe
oddělit částice hmoty a antihmoty. Protože se ale stále jedná o experiment,
potřebovali by ověřit, zda jsou od sebe odděleny skutečně dokonale. Pro jednoduchost
budeme uvažovat jen částice ve dvourozměrném prostoru.
Dostanete k dispozici seznamy částic hmoty a částic antihmoty. Každá částice je
popsána dvěma čísly, které představují její souřadnice. Hledáme přímku, která
rozdělí plochu tak, že všechny částice hmoty jsou na jedné straně a všechny
částice antihmoty na druhé straně. Zjistěte, zda taková přímka vůbec existuje,
a pokud ano, určete její pozici.
 Lehčí varianta (za 7 bodů): Zjistěte jen, zda přímka existuje, nebo ne.
Lehčí varianta (za 7 bodů): Zjistěte jen, zda přímka existuje, nebo ne.
Řešení
Tohle mi nějaký čas zabralo. Jakmile jsem poslal řešení, notebook potemněl. Nic
nenasvědčuje tomu, že bych měl teď něco dělat. Slyším, že za dveřmi neustále
někdo prochází. Nejspíš to je nějaká frekventovaná chodba. Vůbec, jak může být
tahle základna velká? A kolik lidí tu pracuje? Pokud takové skupině velí
zločinec, jak si zařídí, aby se jeho podřízení třeba nevzbouřili?
 30-3-5 Rozbití skupin (8 bodů)
30-3-5 Rozbití skupin (8 bodů)
Pan Nápověda velí japonské tajné základně, kde se nachází velké množství
personálu z různých částí země. Protože ale své podřízené dvakrát nerozmazluje
co se týče jídla a volného času, má obavy ze vzpoury proti své osobě.
Taková vzpoura by vyžadovala součinnost více lidí a Nápověda si všiml, že
nejvíce si na základně rozumí lidé se stejným místem původu. Chtěl by proto
snížit pravděpodobnost toho, že se takoví lidé budou často setkávat.
Základnu tvoří jedna dlouhá chodba, na níž se za sebou nachází N stolů, každý
stůl připravený pro jednoho zaměstance. Každý zaměstanec může pocházet právě
z jednoho z P různých míst původu. V aktuální situaci jsou některé stoly
neobsazené, jiné jsou obsazeny zaměstancem, jehož místo původu známe.
Nápověda chce přijmout zaměstance na každé zatím neobsazené pracovní místo,
přičemž u každého místa si může vybrat, z jakého místa původu bude pocházet
nový pracovník. Aby se však zaměstanci nemohli tak snadno domluvit na
převratu, má Nápověda požadavek: nikdy nesmí dojít k tomu, aby vedle sebe
sedělo více než M zaměstanců se stejným místem původu. Zároveň ale nechce
přesouvat zaměstance, kteří už na základně pracují.
Pro zadané N, M, P a popořadě popis každého stolu (neobsazený/obsazený
zaměstancem s nějakým místem původu) zjistěte, kolik existuje různých možností,
jak doobsadit prázdné stoly, aby byl zachovaný Nápovědův požadavek. Dvě
možnosti doobsazení jsou různé, pokud se alespoň u jednoho zaměstance liší
místo původu.
Příklad: Máme N = 7, M = 2, P = 2, a chodbu zadanou takto:
ABB.AB. (A a B označují dvě různá místa původu, tečka
prázdné místo). Existují dvě různá řešení: ABBAABA a ABBAABB.
Prázdné místo nalevo musí být doplněné „áčkem“, protože by se jinak vyskytla
tři „béčka“ vedle sebe. Prázdné místo napravo může být doplněné jakkoliv.
Řešení
Ozve se divné plácnutí a já uvidím, že na zem spadla nějaká věc. No ne! To je
bageta, kterou jsem měl na koleji! Jak se tady asi vzala?
Odpověď přijde vzápětí. Z rohu naproti místu, kde sedím, přijde záblesk a do
cely se vkutálí Jirka. Další záblesk a vedle něj přistane Filip. Mám tu
zachránce!
„Já jsem měl tušení, že to tvoje těžítko byl nějaký teleportér,“ řekne
Filip, „ale nevěřil jsem tomu, že by se Nápověda dostal technicky takhle
daleko. Když jsi zmizel, tak ten teleportér zůstal na tvém stole. Rychle jsem
ho rozebral a trochu zbastlil, aby dokázal přenášet lidi do tvé blízkosti. Pak
jsem poslal bagetu, abych si ověřil, že to funguje.“
„Ale jak se dostaneme zpátky?“ zajímá mě. Jirka z kapsy vytáhne předmět o velikosti
těžítka, podobný tomu mému. „Naštěstí byl ve věcech z bunkru ještě jeden
teleportér. Vezme nás zpátky do Prahy na koleje. Ale není čas na nějaké řeči,
hned musíme pryč!“ Jirka natáhne ruku, aby byl teleportér mezi námi, a chce ho
spustit, když vtom se otevřou dveře a v nich stojí Nápověda. V ruce drží
povědomou krabičku a já znovu cítím, jak mám ztuhlé a nehybné nohy. Jirkovi
vypadne teleportér z ruky a spadne na zem. Nestihli jsme to!
„Vida, další návštěva z Prahy,“ řekne. „Moc díky za vyřešení úlohy,“
obrátí se na mě. „To je poslední věc, která ještě byla potřeba pro
dokončení antihmotové bomby. Určitě víš, co se stane, když se srazí hmota
s antihmotou – uvolní všechnu svoji energii.“
Nápověda si všimne teleportéru, který Jirkovi spadl na zem. „Výborně, tímhle
jste se chtěli dostat domů? Technologie na výrobu teleportérů se vyrábí dost
těžko a jen tak bych si ji tu neobstaral… ale vy jste mi o mnoho ulehčili
práci.“
Za Nápovědou se objeví člověk poměrně malého vzrůstu, není mu moc v tom šeru
pořádně vidět do tváře. Předá Nápovědovi podivný, kulatý předmět. „Co asi
bude dělat tahle krabička?“ ptám se.
„Tahle krabička dokáže vyhodit do vzduchu pár budov v centru města. Nic
moc? Tak ji zvětšíme na dvojnásobek a už dokáže srovnat se zemí celou městskou
čtvrť. Další pokračování si jistě dokážete představit. A když už tady máte ten
zbastlený teleportér, rovnou tu bombu pošlu přes něj. Bude to taková malá
zkouška.“
To je konec, dívám se na Jirku. Co by nám teď mohlo pomoci?
Temnotu místnosti přeruší záblesk. Z něj se prudce vyřítí další člověk. To je
Janka! Jak nemůže zastavit, porazí Nápovědu na zem. Zmateně na nás zamžourá.
„Na stole ste mali také divné…“
„Nemusíš nic vysvětlovat,“ přeruší ji Jirka. Jak Nápověda spadl, muselo se
mu něco stát se zmrazovačem. Už se zase můžeme hýbat. Na nic nečekám a chňapnu
po teleportéru, který byl až dosud v držení pana Nápovědy. Předám ho Jirkovi,
ten zakřičí: „Vezměte se za ruce!“ Všímám si, že bomba, která taky vypadla
padouchovi z rukou, začala slabě zářit a bzučet. Ale to už Jirka zapnul
teleportér a mizíme pryč, do bezpečí!
* * *
Nedaleko Tokia došlo k podzemnímu výbuchu, japonská armáda tvrdí, že
o ničem neví, čtu na displeji telefonu. Oblast prý byla uzavřena a je pod přísnou
ochranou, některým novinářům se ale přece jenom podařilo proniknout dovnitř
a nafotit zbytky něčeho, co vypadá jako tajná základna.
 30-3-6 Střežení oblasti (11 bodů)
30-3-6 Střežení oblasti (11 bodů)
Japonská policie se snaží zamezit vstupu do ohraničené oblasti, kde se
vyskytovala základna. Má ale málo personálu, a tak chce posílat své lidi jen na
ty části hranice, kam zrovna vyjeli zvědaví novináři. To se navíc může v čase
měnit.
Představte si hranici jako nekonečnou přímku s počátkem, jakýkoliv bod na
přímce lze jednoznačně určit podle vzdálenosti od počátku (ta je kladná, pokud
je bod napravo od počátku, nebo záporná, pokud je nalevo). Na tuto hranici
posíláme hlídkovat stráž. Jejich velitel po sobě zadává N instrukcí, každá
buď „hlídejte hranici mezi body A a B“, nebo „přestaňte hlídat
hranici mezi body A a B“. A je vždy menší než B (tj. bod určující A
je vždy nalevo od B). Na začátku se nehlídá žádná část hranice.
Může se stát, že kvůli první instrukci se sloučí dva nebo víc hlídaných úseků
do jediného dlouhého úseku, naopak druhá instrukce může rozdělit jeden souvislý
úsek do menších úseků. Také lze nařídit hlídání oblasti, která už (třeba jen
zčásti) hlídaná je, nebo zastavit hlídání oblasti, která (třeba jen zčásti)
hlídaná není.
Chceme, abyste po každé instrukci odpověděli, kolik je souvislých oblastí,
které jsou střežené.
Například můžete dostat následující řadu instrukcí. Vpravo od instrukce se nachází
počet souvisle střežených oblastí po provedení instrukce.
| Hlídejte [0,1] | 1 |
| Hlídejte [2,4] | 2 |
| Hlídejte [1,3] | 1 |
| Hlídejte [10,20] | 2 |
| Přestaňte hlídat [15,16] | 3 |
Řešení
Tohle dobrodružství mi zabralo skoro celou noc. Cítím se jako zombík a podobně
asi vypadám, ale je dost možné, že jsme Nápovědu konečně zničili. Za chvíli mi
začíná ta zkouška, na kterou jsem se učil, tak uvidíme, jaký bude výsledek.
Nemá někdo po ruce bagetu?
Kuba Maroušek
 30-3-7 Funkce očima assembleru (15 bodů)
30-3-7 Funkce očima assembleru (15 bodů)
Ve druhém dílu seriálu jsme se naučili základní operace s pamětí, takže již
umíme napsat program, který opravdu dělá něco užitečného – například řadí
čísla podle velikosti. Tentokrát se naučíme vytvářet a volat funkce.
To je asi poslední důležitá konstrukce
z běžných (procedurálních) programovacích jazyků, na kterou jsme se zatím
nepodívali.
Pravděpodobně jste se s funkcemi ve svém programátorském životě již setkali,
takže je nemusíme složitě představovat. Funkce je zkrátka blok kódu, kterému
na začátku předáme vstupy (argumenty), on je zpracuje a něco z nich spočítá.
Navíc může provést nějaký vedlejší efekt, například vypsat číslo na obrazovku.
Funkce nám umožňují členit si práci na menší části, takže nemusíme při
programování myslet na všechny detaily najednou. A také díky nim můžeme snadno
zamezit opakování kódu – pokud stejné operace potřebujeme provádět na více
místech, jednoduše místo opakování celé posloupnosti instrukcí vždy zavoláme
tutéž funkci.
První pokus o funkci
Jak si pořídit něco jako funkci v assembleru? Pojďme to vyzkoušet na
triviálním příkladu funkce, která dostane dvě čísla a vrátí jejich součet.
Především se dohodneme, že vstupy budeme předávat v registrech r0 a r1
a výsledek vrátíme v r0. Na nějaké místo v programu napíšeme kód naší funkce
a označíme jeho začátek návěštím odpovídajícím názvu funkce.
Samotné zavolání bychom pak provedli uložením parametrů do správných registrů
a skokem na ono návěští. Tím ale ještě zdaleka nemáme vyhráno. Hlavní výhoda
funkcí spočívá v tom, že jednu funkci můžeme zavolat z více míst v kódu.
Funkce se tedy musí umět vrátit na to místo, odkud jsme ji zavolali.
Jak to pozná? Mohlo by nás napadnout funkci předat jako jeden z parametrů
adresu, na kterou se má vrátit (tzv. návratovou adresu). To je adresa
instrukce následující hned po skoku, který funkci zavolal. Funkce by tedy
provedla svou práci a na závěr by jen skočila na adresu, kterou takto dostala
v některém registru (musíme mít samozřejmě předem domluveno ve kterém,
tak použijme třeba r2).
Pro tento závěrečný skok existuje instrukce BX (Branch and
eXchange). Proč má v názvu zrovna exchange, je na delší povídání a teď to
není důležité. Zatím se spokojíme s tím, že jako argument bere registr
a provede skok na adresu, která je v něm uložena.
Když si vzpomeneme, že při čtení registru pc dostaneme automaticky adresu,
která je o dvě instrukce dál, dostaneme velmi jednoduchý kód, kterým funkci předáme
správnou návratovou adresu. Naše první funkce bude vypadat následovně.
MOV r0, #123 @ první argument
MOV r1, #456 @ druhý argument
MOV r2, pc @ adresa instrukce MOV r3, r0
B secti
MOV r3, r0 @ výsledek funkce uložíme do r3
B konec
secti:
ADD r0, r1 @ funkce vrací výsledek v r0
BX r2
konec:
Všimněte si nepodmíněného skoku na návěští konec. V našem simulátoru program
skončí tím, že dojde na konec souboru. Kdybychom skok vynechali, bude se po
provedení MOV r3, r0 automaticky provádět následující instrukce, což by
byla naše funkce na sčítání. Tentokrát by jí ale nikdo nepředal novou
informaci o návratové adrese, takže by skočila opět na stejné místo a celý
program by se tak zacyklil.
Protože volání a návrat z funkcí je velmi častá operace a nebyli jsme první,
koho napadlo předávat funkci návratovou adresu v nějakém registru, je na ARMu
zvykem používat k tomuto účelu registr r14 přezdívaný také lr
(Link Register). Pak můžeme pro samotné volání použít šikovnou instrukci
BL (Branch with Link), která sama uloží správnou návratovou adresu
do lr a pak skočí na zadané místo.
Náš příklad se sčítáním bychom pomocí BL mohli zjednodušit takto:
MOV r0, #123
MOV r1, #456
BL secti
MOV r3, r0
B konec
secti:
ADD r0, r1
BX lr
konec:
Zásobník
Všimněte si, že dosud je celý náš kód vzájemně velmi provázaný.
Musíme pořád myslet na to, které registry kde na co používáme,
abychom jejich obsah nedopatřením nepřepsali něčím jiným.
To je s rostoucí velikostí programu čím dál těžší.
Brzy také v popsaném postupu narazíme na jednu slabinu. Jak z jedné funkce
zavolat funkci jinou tak, abychom si nepřepsali návratovou adresu v link
registru? Mohli bychom si ji před zavoláním funkce někam uložit. Ale kam,
abychom si ji nepřepsali tam?
S řešením nám pomůže zásobník. Možná jste o něm již někdy něco zaslechli.
V plné (informatické) obecnosti je to datová struktura, do které můžeme
v nějakém pořadí ukládat data a v opačném je zase vybírat – tedy poslední vložený
prvek bude první, který vyndáme.
Zásobník si zvládneme vyrobit sami. Vyhradíme pro něj souvislou oblast paměti
a dohodneme se, že ji budeme zaplňovat shora dolů (od nejvyšších adres k nejnižším).
Jedním registrem si budeme ukazovat na vrchol zásobníku, tedy poslední vloženou
hodnotu. Nenechte se mýlit tím, že vrchol zásobníku leží na nejnižší využité adrese.
Vložení prvku na zásobník pak bude spočívat ve snížení tohoto ukazatele
a uložení nové hodnoty. A naopak vyndání prvku nejprve načte hodnotu a poté
zvýší ukazatel na vrchol zásobníku.
Důležité je uvědomit si, že zásobník nám stačí jeden, společný pro celý program.
Libovolné funkci dovolíme si na něj uložit, cokoliv potřebuje, pod jednou podmínkou:
než funkce skončí, musí vždy ze zásobníku odebrat vše, co do něj sama přidala.
Tím zaručíme, že když si na zásobník něco odložíme na začátku funkce,
například hodnotu link registru, a následně zavoláme nějaké další funkce, tak
na závěr můžeme ze zásobníku naše data zase bez problému přečíst,
aniž bychom museli hledat, kde jsou.
Zbývá se domluvit, který registr budeme používat jako ukazatel na zásobník.
Protože se zásobníkem samozřejmě návrháři ARMu také počítali, vyhradili pro
něj registr r13 a zavedli pro něj přezdívku sp (Stack Pointer).
K ukládání na zásobník se hodí instrukce PUSH {registr}. Ta odečte
od sp 4 a na takto spočítanou adresu zapíše obsah zadaného registru.
Instrukce POP {registr} provede inverzní operaci: z adresy uložené
v sp přečte číslo, uloží ho do registru a nakonec zvýší sp o 4.
To se dá zapsat i jinými instrukcemi: Místo PUSH {registr} bychom mohli
provést STR registr,[sp,#-4]! a instrukci POP {registr}
nahradit za LDR registr,[sp],#4.
Skutečný PUSH a POP jsou ovšem mnohem mocnější: do složených závorek
můžete napsat více registrů, například PUSH {r0-r3,r7}.
Dodejme, že registry jsou do paměti uloženy v rostoucím pořadí čísel, ten s nejmenším
číslem skončí na nejnižší adrese, tedy na vrcholu zásobníku.
Ještě dodejme, že na některých jiných architekturách procesorů se zásobník používá
i k ukládání návratové adresy z funkce (místo lr). Obvykle existuje instrukce
CALL, která PUSHne návratovou adresu a skočí na začátek funkce,
a instrukce RET, která POPne adresu a skočí na ni.
Rekurzivní funkce: faktoriál
Dejme to všechno dohromady a pojďme si napsat funkci počítající faktoriál
čísla (Faktoriál z n se značí n! a je roven 1·2·3·… ·n.).
Obdobně jako v předchozím případě dostane argument v registru r0
a také v něm vrátí výsledek.
Funkci napíšeme s využitím rekurze – bude volat sama sebe. Faktoriál čísel 0
a 1 je jednoduchý, je to jednička. Pro všechna ostatní čísla využijeme
toho, že n! = n ·(n-1)!.
Celý kód včetně volání funkce bude vypadat následovně:
MOV r0, #7 @ Spočítáme faktoriál sedmi
BL faktorial
@ ... zde pokračuje hlavní program
faktorial:
CMP r0, #1 @ porovnáme vstup (n) s 1
MOVLS r0, #1 @ pro 0 a 1 vrátíme 1
BXLS lr @ a hned skončíme
PUSH {r4, lr} @ uložíme registry na zásobník
MOV r4, r0 @ r4 = n
SUB r0, #1 @ r0 = n-1
BL faktorial @ r0 = (n-1)!
MUL r0, r4 @ r0 = n*(n-1)!
POP {r4, lr}
BX lr
Nejprve porovnáme argument funkce s číslem 1. Pokud je menší nebo roven, chceme
vrátit jedničku. Protože návratovou hodnotu předáváme ve stejném
registru, v jakém dostaneme argument funkce, stačí nám provést dvojici instrukcí
MOV r0, #1 a BX lr a máme hotovo. V příkladu výše se vyhýbáme
dalšímu skákání a obě instrukce zapisujeme rovnou
v podmíněné variantě, takže se provedou právě tehdy, kdy je r0 ≤ 1.
Následně uložíme na zásobník ty registry, které budeme v průběhu měnit.
Protože budeme volat funkci s argumentem n - 1, potřebujeme si někde (v našem
případě v r4) uložit původní hodnotu z r0. Pak zavoláme
funkci faktorial na o jedna menším čísle a až se vrátí, výsledek
vynásobíme zapamatovanou hodnotou.
Na závěr zbývá vrátit zásobník a registry r4 a lr do
původního stavu a vrátit se skokem na adresu v lr.
Volací konvence
Při programování funkcí jsme vždy museli určit, ve kterých registrech se předává
který argument a kde výsledek. Bylo by ale nešikovné pokaždé to vymýšlet znovu
a u každé funkce, kterou voláme, vzpomínat, jaké má rozhraní. Proto se lidé shodli
na takzvané volací konvenci – souboru pravidel určujících, jak se volají
funkce.
Na ARMu je situace jednoduchá, protože konvence vznikla spolu s procesorem
a používají ji prakticky všichni: nejen programátoři v assembleru, ale i autoři
překladačů dalších programovacích jazyků.
(Jinde to může být jinak: pro architekturu x86 existuje mnoho různých konvencí
pro různé operační systémy a programovací jazyky.)
Význam registrů r14 (lr) a r13 (sp) jsme si již
prozradili. První – link register – obsahuje adresu, na kterou se má funkce
vrátit. Pokud tedy funkce chce zavolat jinou funkci, musí si tuto hodnotu někam
uložit.
Druhý – stack pointer – ukazuje stále na zásobník a musíme jej vrátit ve
stejném stavu, v jakém jsme jej dostali. To zaručíme nejlépe tím, že funkce
vždy zavolá instrukci POP na tolik hodnot, kolik jich tam předtím sama
uložila pomocí PUSH.
Registry r0-r3 se používají (postupně) na předání prvních čtyř
argumentů funkce a slouží i pro návratovou hodnotu. Právě kvůli
využití jako argumenty, existují pro tyto registry ještě alternativní jména
a1-a4 (pozor na posun čísel o jedna). Se všemi těmito čtyřmi registry
si funkce může dělat, co chce. Můžete si do nich klidně ukládat mezivýsledky
a nikdo se nebude zlobit, když je nevrátíte v původním stavu.
Registry r4-r11 jsou určené pro ukládání lokálních proměnných uvnitř
funkce. Funkce je musí vrátit ve stejném stavu, v jakém je dostala. Právě díky
využití registrů r4-r11 pro lokální proměnné (variable) dostaly
tyto registry ještě alternativní názvy v1-v8. Silně doporučujeme používat
pouze jeden typ jmen, jinak se v číslování snadno ztratíte. My zůstaneme
u názvů s písmenem r. (Pro úplnost poznamenejme, že registr r9
může mít někdy speciální význam a není pak pro funkce použitelný ani jako
proměnná. V našem prostředí se to ale nestane.)
Těchto volacích konvencí jsme se drželi již v příkladu s výpočtem faktoriálu.
Před použitím registru r4 pro lokální proměnnou jsme ho uložili na
zásobník. Díky tomu jsme ale měli zaručeno, že nám její hodnotu naše funkce
sama nezmění.
Zbývá nám registr r12, čili takzvaný Intra-Procedure call scratch
register alias ip. To nám říká, že se s ním během volání funkce může stát cokoli.
Používá se třeba při volání funkcí z dynamicky linkovaných knihoven (k přesnému
mechanismu se v našem úvodním seriálu nedostaneme). Pokud ale píšete krátkou funkci,
která již nic dalšího nevolá, můžete tedy použít i tento registr zcela dle libosti.
Vynechali jsme ještě registr r15 (pc), který se přirozeně posouvá
s každou instrukcí, takže nemá smysl jej příliš rozebírat.
Úkol 1 [2b]
Napište funkci, která dostane dva parametry: číslo N≥ 3 a adresu A.
Funkce přečte N-prvkové pole čísel uložené od adresy A a vrátí jako
výsledek třetí největší číslo. Řiďte se volací konvencí.
Intermezzo #1: Instrukce LDM a STM
Mimochodem, instrukce PUSH a POP jsou jenom speciální případy
mnohem obecnějšího mechanismu pro přenos více registrů najednou. Jelikož se
nám bude za chvíli hodit, pojďme se na něj podívat pořádně.
Jedná se o osm instrukcí tvaru
(LD|ST)M(I|D)(B|A) registr!, {seznam registrů}
První dvě písmena říkají, zda se data budou načítat z paměti (LoaD), nebo ukládat do paměti (STore).
Zadaný registr určuje adresu v paměti, ale ta se ještě zvýší (Increment) nebo sníží (Decrement),
a to před použitím (Before) nebo po něm (After). Pokud je uveden vykřičník, adresa se následně
zapíše zpět do registru. Registry v seznamu jsou zpracovávány postupně, v režimu I od nejnižšího
čísla k nejvyššímu, v režimu D opačně.
Například LDMIA sp!, {r0,r1} vezme adresu z sp, přečte z ní číslo do r0,
pak ji zvýší o 4, přečte z ní číslo do r1, opět ji zvýší o 4 a nakonec ji uloží zpět
do sp. Je to tedy POP. Podobně STMDB sp!, {r0,r1} je PUSH.
Úkol 2 [3b]
Napište co nejrychlejší funkci, která vyplní velký blok paměti nulami. Jako
argumenty dostane počáteční adresu bloku a jeho velikost v bajtech. Dodržujte
volací konvenci. Minimalizujte celkový počet provedených instrukcí, ale nepoužívejte
nezarovnané přístupy k paměti (třeba čtení 32-bitového čísla z adresy, která není
dělitelná čtyřmi).
Intermezzo #2: Daleká cesta za konstantami
Ještě si dopřejme jednu odbočku. Zatím jsme v programech používali všelijaké
konstanty, ale až na konci minulého dílu jsme si přiznali, že přímo do instrukce
jdou zakódovat jen ve speciálních případech. Podívejme se, co si počít, když se
konstanta do instrukce nevejde.
Jedna z možností je konstantu do registru dostat nadvakrát. K tomu slouží
instrukce MOVW registr, #hodnota
a MOVT registr, #hodnota. Obě jsou zakódované speciálním
způsobem, takže hodnota může být libovolné 16-bitové číslo. Přitom MOVW toto
číslo uloží do nižších 16 bitů registru a vyšších 16 vyplní nulami, zatímco MOVT
uloží číslo do vyšších 16 bitů a nižších 16 nechá na pokoji. Můžeme tedy udělat třeba
MOVW R0, #0x5678 @ R0 = 0x00005678
MOVT R0, #0x1234 @ R0 = 0x12345678
Kdybychom chtěli do registru dostat adresu nějakého návěští, můžeme si ji
od překladače nechat rozpůlit:
MOVW R0, #:lower16:funkce
MOVT R0, #:upper16:funkce
Další způsob je říci překladači, ať konstantu uloží do paměti jako posloupnost
bajtů, a pak ji odtamtud přečíst. Zkusme do programu napsat
.BYTE 0x12, 0x34, 0x56, 0x78
.WORD 0xABADCAFE
.ASCII "kolemdokola"
.ALIGN 4
Tím jsme řekli překladači, aby místo instrukcí vygeneroval nejprve čtyři
bajty s určenými hodnotami, pak určené 32-bitové slovo, posloupnost
bajtů kódujících znaky řetězce (pozor, není ukončena nulovým bajtem)
a nakonec zarovnání na adresu dělitelnou čtyřmi
– to je potřeba, pokud za tímto blokem následují ještě nějaké instrukce,
ty musí být zarovnané.
Všimněte si tečky na začátku: ta překladači říká, že nemá očekávat instrukci
assembleru, nýbrž direktivu překladače.
Pro přečtení konstanty se hodí jedna speciální forma instrukce LDR.
Ta se v assembleru píše jako
LDR cílový-registr, zdrojová-adresa
ale ve skutečnosti se přeloží na adresu vypočítanou sečtením pc
s malým offsetem uloženým v instrukci. Můžeme se pomocí ní tedy snadno
odkazovat na data uložená v paměti blízko instrukce, která je používá.
Samozřejmě si musíme dávat pozor na to, aby se procesor data nepokoušel
provádět jako instrukce. Šikovné místo pro data tudíž leží za instrukcí
BX uzavírající funkci.
Pojďme se podívat na příklad: následující funkce vynásobí svůj argument
rychlostí světla.
nasob_c:
LDR R1, rychlost_svetla
MUL R0, R1 @ výsledek = argument * R1
BX lr
rychlost_svetla:
.WORD 299792458 @ m/s
Jako konstantu můžete použít i adresu nějakého návěští, např.
.WORD nasob_c.
Existuje milá zkratka:
LDR cílový-registr, =konstanta
Ta načte do registru danou konstantu, která může být libovolné
32-bitové číslo (případně návěští). Proč jsme vymýšleli kolem konstant takové
komplikace, když se to dá zařídit jednou instrukcí? On je to tak
trochu podvod a tato zkratka není instrukce. Ve skutečnosti se
LDR r0, =0x12345678 přeloží na:
LDR r0, const_1
...
const_1:
.WORD 0x12345678
Jen vám kompilátor sám najde pro uložení konstanty v programu vhodné
místo (typicky taky za koncem funkce).
Kam s ním? aneb zase zásobník
Když jsme popisovali volací konvenci, tiše jsme předpokládali, že argumenty
funkce jsou nejvýše čtyři a každý z nich se vejde do 32-bitového registru.
Co si počneme, když na tato omezení narazíme?
S rozměrnějšími datovými typy si poradíme snadno: předáme je rozsekané
ve více registrech. To by se mohlo hodit, kdybychom chtěli počítat třeba
s 64-bitovými čísly.
Horší je, když nám dojdou registry vyhrazené pro předávání argumentů
(přeci jenom, jsou jenom čtyři). Tehdy konvence káže předat zbývající
argumenty na zásobníku, a to tak, aby první z nich byl uložený na nejnižší
adrese. Pokud je tedy budeme ukládat instrukcí PUSH, musíme začít
posledním argumentem.
Zavolaná funkce si argumenty ze zásobníku přečte, ale ponechá je tam (k tomu se
hodí instrukce LDMIA bez vykřičníku). Odstranění ze zásobníku má na
starost volající, až mu funkce zase předá řízení. Tím pádem se funkce nerozbije,
pokud jí někdo předá více parametrů, než čekala.
Podobně si poradíme, pokud naše funkce potřebuje víc lokálních proměnných,
než se jí vejde do registrů. Prostě si vyhradí místo na zásobníku odečtením
od sp a do tohoto místa ukládá své proměnné, které adresuje relativně
k sp. Také místo může využívat na argumenty podřízených funkcí.
Než se vrátí, uvede sp do původního stavu.
Někdy je nepohodlné, že sp se neustále mění při dočasném odkládání
hodnot na zásobník různými PUSHi. Tehdy může být příjemnější zkopírovat
si na začátku funkce sp do nějakého jiného registru a adresovat pomocí něj
(na kladných offsetech jsou pak argumenty, na záporných lokální proměnné).
Často se k tomu používá registr r11, říká se mu frame pointer
a v této roli se značí fp.
Podívejme se na příklad funkce s argumenty x1,… ,x6, která vrátí
největší z x4, x5, x6. Hodí se nám použít podmíněnou variantu instrukce MOV.
MOV r0, #5 @ x_5
MOV r1, #6 @ x_6
PUSH {r0,r1} @ na zásobníku x_5 a x_6
MOV r0, #1 @ x_1
@ podobně r1-r3 pro x_2 až x_4
BL max456
ADD sp, #8 @ smažeme x_5 a x_6
@ ... zbytek programu
max456:
PUSH {r4,r5,fp} @ uložíme, co budeme měnit
ADD fp, sp, #12 @ fp ukazuje na původní sp
LDMIA fp, {r4,r5} @ přečteme x_5 a x_6
MOV r0, r3 @ x_4
CMP r0, r4 @ x_5
MOVLO r0, r4
CMP r0, r5 @ x_6
MOVLO r0, r5
POP {r4,r5,fp}
BX lr
Úkol 3 [3b]
Napište funkci s proměnlivým počtem argumentů, která vrátí součet všech
svých argumentů. Jelikož nemůže poznat, kolik argumentů dostala, zastaví
se na prvním nulovém argumentu.
Krutá pravda o našem simulátoru
Nemůžeme to déle skrývat, pravda musí vyjít najevo: náš simulátor assembleru
(http://ksp.mff.cuni.cz/viz/asm)
je ve skutečnosti překladačem Céčka, do kterého jsou jenom vložené assemblerské
instrukce (pomocí GCCčkové direktivy asm). Okolo assemblerských instrukcí
se nachází jednoduchá obálka, která jenom posbírá hodnoty z registrů a předá je
k vypsání obyčejné Céčkové funkci printf.
Takové printf je typickým příkladem funkce s proměnlivým počtem argumentů.
Jako první argument dostane formátovací řetězec (přesně řečeno ukazatel na místo
v paměti, kde začíná posloupnost znaků ukončená nulovým bajtem). Tento řetězec
vypíše a kdykoliv v něm narazí na nějakou kombinaci znaků začínajících procentem,
vypíše místo ní další argument. Speciálně %d nechá vypsat číslo v desítkové
soustavě, %x šestnáctkové číslo a %s řetězec.
Nejspíš už vás to napadlo, ale pro jistotu dodáme, že název libovolné Céčkové
funkce lze použít jako návěští a dá se s ním dělat cokoli, co s assemblerovými
návěštími – např. na něj skočit.
Úkol 4 [3b]
Když je simulátor takový švindl, který si jen tak volá Céčkové printf,
pojďme si ho ze simulovaného assembleru také zavolat. Napište program, který
v simulátoru vypíše 100 číslovaných řádků s textem „Nebudu si číst pod
lavicí popis instrukční sady ARMu.“.
V králíka se proměň!
Nakonec se podíváme na jednu specialitu: programy, které modifikují samy
sebe. Teoreticky to není nic podivného – stejně jako jakákoliv data,
program je v paměti také uložen jako posloupnost bajtů, takže do něj jde
zapisovat (tedy pokud nám to operační systém nezakáže). V praxi se toho
často využívá: nahráváme-li nový program z disku do paměti, nebo třeba
když debugger potřebuje do programu umístit breakpoint.
Pojďme si to také vyzkoušet, ale abychom se vyhnuli záhadným chybám,
prozradíme, že mezi vytvořením instrukcí v paměti a jejich spuštěním
musí proběhnout dvojice instrukcí DSB a ISB. Ty zabrání
situacím typu „procesor si instrukce přečetl v předstihu a začal
je provádět, aniž si všiml, že se pak ještě změnily“. Též připomínáme,
že cílová adresa v instrukci skoku je kódovaná relativně vůči její
vlastní adrese, takže pokud takovou instrukci překopírujete jinam,
bude skákat jinam.
Úkol 5 [4b]
Napište program pro simulátor, který v paměti upraví funkci printf
tak, aby vypisované řádky číslovala. Prozradíme vám, že tato funkce začíná
instrukcí PUSH {r0-r3}.
Jenda Hadrava & Martin Mareš
Řešení
 30-3-1 Vlnění (9 bodů)
30-3-1 Vlnění (9 bodů) 30-3-2 Zmrazovač (10 bodů)
30-3-2 Zmrazovač (10 bodů)
 Jednomu z pracovních týmů pana Nápovědy se podařilo najít způsob, jak od sebe
oddělit částice hmoty a antihmoty. Protože se ale stále jedná o experiment,
potřebovali by ověřit, zda jsou od sebe odděleny skutečně dokonale. Pro jednoduchost
budeme uvažovat jen částice ve dvourozměrném prostoru.
Jednomu z pracovních týmů pana Nápovědy se podařilo najít způsob, jak od sebe
oddělit částice hmoty a antihmoty. Protože se ale stále jedná o experiment,
potřebovali by ověřit, zda jsou od sebe odděleny skutečně dokonale. Pro jednoduchost
budeme uvažovat jen částice ve dvourozměrném prostoru. Lehčí varianta (za 7 bodů): Zjistěte jen, zda přímka existuje, nebo ne.
Lehčí varianta (za 7 bodů): Zjistěte jen, zda přímka existuje, nebo ne. 30-3-7 Funkce očima assembleru (15 bodů)
30-3-7 Funkce očima assembleru (15 bodů)