První série třicátého prvního ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
První sníh už dávno napadl a zase roztál, Vánoce a nový rok už klepou na dveře a organizátoři si konečně našli čas na opravení vašich řešení první série. Za způsobenou prodlevu se vám omlouváme.
Právě si prohlížíte historicky první komentáře k úlohám, konkrétně úlohám letošní první série hlavní kategorie. Od letoška jsou totiž řešení každé série rozdělena na dvě části: na samotná autorská řešení, která vydáváme brzy po termínu série, a komentáře k došlým řešením, která vydáváme až po opravení vašich řešení.
Pokud se vám cokoliv nezdá nebo máte nějaký dotaz, neváhejte se ozvat na našem fóru nebo emailem na známou adresu.
Komentáře k úlohám
- 31-1-2: Skoro nejkratší cesta
- 31-1-3: Řazení kořenek
- 31-1-4: Myslivci
- 31-1-5: Krájení bábovky
- 31-1-6: Hroznýšovo okno
 31-1-2 Skoro nejkratší cesta (Zadání) (Řešení)
31-1-2 Skoro nejkratší cesta (Zadání) (Řešení)
Hlavním problémem bylo, že málokdo přečetl správně zadání úlohy, které se ptalo na počet cest, nikoliv na cesty. To je problém, protože cest může být i exponenciálně mnoho (viz graf níže).
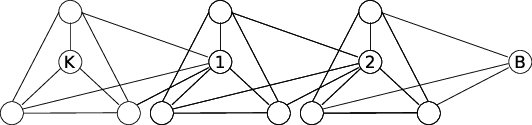
Jinak se sešla pěkná řešení, která úlohu řešila jedním ze tří způsobů:
- Ekvivaletně ke vzorovému řešení.
- Někteří řešitelé si všimli, že lze napočítat cesty a délky od B (babiččin vrchol) a od K (Karkulčin vrchol) pomocí BFS (tak, jak je to popsáno ve vzorovém řešení). Pak můžeme projít každou hranu (z u do v), a pokud by tato hrana prodloužila cesty z K do u a z v do B na skoro nejkratší, tak vynásobením počtu nejkratších cest mezi K a u a počtu nejkratších cest mezi B a v zjistíme počet skoro nejkratších cest přes vrcholy u a v.
- Další přístup byl počítání cest délky k pro k = 1 až k = ℓ+ 1, kde ℓ je délka nejkratší cesty z K do B, tu si můžeme spočítat například pomocí BFS.
 31-1-3 Řazení kořenek (Zadání) (Řešení)
31-1-3 Řazení kořenek (Zadání) (Řešení)
Většina funkčních řešení byla podobná tomu vzorovému: našla nejdelší rostoucí podposloupnost (více čí méně efektivně) a pak vypsala, jak popřesouvat zbývající kořenky. Vypisování se málokdo věnoval pečlivě – konec konců, ze zadání nebylo jasné, co přesně se má vypsat. Ale jak je vidět ze vzorového řešení, vypisování je nakonec ta nejzajímavější část úlohy. Proto jsme těm, kdo ho zvládli správně a rychle, přidělili jeden bod nad maximum.
Dynamické programování
Se zajímavým řešením přišel Pepa Minařík. Nechť a1,… ,an je permutace k setřídění a ak její nejmenší prvek. Ten musíme nějak dostat na začátek, což lze učinit dvěma způsoby:
- Buďto někdy (bez újmy na obecnosti hned na začátku) přesuneme ak před všechny ostatní prvky. Pak zbývá dotřídit posloupnost a1,… ,ak-1,ak+1,… ,an.
- Anebo to neuděláme, ale pak musíme někdy (bez újmy na obecnosti úplně na konci) přesunout prvky a1,… ,ak-1. Tehdy už musí být setříděné ak+1,… ,an.
Označíme-li minimální počet přesunů P(a1,a2,… ,an), musí tedy platit
Nabízí se založit na tomto vztahu dynamické programování: počítat P od nejkratších posloupností k těm nejdelším. Na první pohled to vypadá, že ho budeme muset spočítat pro exponenciálně mnoho posloupností. Zachrání nás ovšem, že všechny z nich vzniknou ze zadané permutace vynecháním nejmenších ℓ prvků a následně zahozením prvních m prvků. Jsou tedy jednoznačně určené parametry ℓ a m, takže jich je jenom O(n2).
Rozmyslete si, že pokud si dvojice (ℓ,m) šikovně uspořádáme, dokážeme každé P(… ) spočítat v konstantním čase. Vyjde z toho poměrně jednoduchý kvadratický algoritmus. Pokud si během něj budeme udržovat, která z variant byla při výpočtu P(… ) ta menší, můžeme snadno odpovědět, jaké přesuny máme provést.
Hladové algoritmy a jiná nefunkční cháska
Nyní se podívejme na některá slibná, ale nefunkční řešení. Můžeme například zkusit použít nějaký třídicí algoritmus, který málo přesouvá. Například Insertsort – třídění vkládáním. Ten ovšem selže na permutaci 4 1 2 3. Vybere nejprve 4 a pak ostatní čísla přesouvá před ni. Spotřebuje tedy 3 přesuny. Stačil by ale jeden: přesunout 4 za ostatní prvky. Podobně se dá vyvrátit optimalita dalších třídicích algoritmů.
Někteří řešitelé také zkoušeli „hladový“ přístup: spočítat pro každé číslo, jak daleko je od své správné pozice, a zahájit přesouvání od toho, které je nejdál. To nefunguje například pro vstup 3 4 1 5 2: nejdále od správné pozice je 2, takže vytvoříme 3 2 4 1 5, což už nejde dotřídit jedním přesunem. Dva přesuny přitom k setřídění vstupu stačí: například přesunout 1 na začátek a pak 2 za 1.
 31-1-4 Myslivci (Zadání) (Řešení)
31-1-4 Myslivci (Zadání) (Řešení)
I přes poměrně velký počet řešení se mi skoro v žádném nepovedlo najít chybu. Asi bylo ze zadání docela jasné, co se má vlastně počítat, což je super. To, že nikdo nezůstal bez bodů, ale neznamená, že by bylo samozřejmé přijít na optimální řešení. Asi všichni, komu se to povedlo, byli blízko jednomu z algoritmů popisovaných ve vzorovém řešení – buď si setřídili obě pole a pak je najednou prošli, a nebo si setřídili jedno z nich a pak v něm binárně vyhledávali odpovídající prvky. První zmíněné bude asi rychlejší v praxi, druhé má zase teoretickou výhodu se strašlivě rozdílnými velikosti vstupů, takže úplně stejná nejsou; plný počet bodů byl ale za obě.
 31-1-5 Krájení bábovky (Zadání) (Řešení)
31-1-5 Krájení bábovky (Zadání) (Řešení)
Úloha byla podle očekávání složitá, takže body dostaly i různé částečné pokusy, pokud fungovaly alespoň v některých rozumně vymezitelných případech (pravidelný mnohoúhelník, čtyřúhelník, …); k tomu asi není co poznamenávat.
Několik řešitelů se však dopustilo předpokladu, který jsme v zadání implicitně vyvraceli obrázkem. Jeden řešitel dokonce měl tolik drzosti, že vyjádřil ještě politování nad nepřesným obrázkem v zadání, za což byl adekvátně ohodnocen sníženou bodovou sazbou. Vězte, že obrázky v zadání se snažíme kreslit tak přesné, jak to je jenom možné, a pokud se tři přímky těsně (leč viditelně) neprotínají v jednom bodě, tak je to proto, že se v tom bodě opravdu neprotínají.
Nyní tedy ukážeme, že v žádném konvexním mnohoúhelníku s konečným počtem stran neexistuje bod, kterým by procházelo více než konečně mnoho dělících úseček. Dělící úsečka je zde taková, jejíž vrcholy leží na obvodu mnohoúhelníka a která dělí mnohoúhelník na dvě části o stejném obsahu.
Definice: Je zadán úhel φ s vrcholem V a polopřímkami Vr a Vs. Je také zadán konstantní obsah S a bod B uvnitř úhlu φ. Přímka p prochází bodem B a protíná polopřímky Vr a Vs v bodech Ri a Si tak, že obsah trojúhelníka VRiSi je roven S.
Tvrzení: Existují nejvýše dvě přímky p pro zadaný úhel φ, obsah S a bod B, které splňují definici.
| 1 |
| qi |
 Ve dvourozměrném vektorovém prostoru s bází tvořenou vektory
VR→ a VS→ si také vyjádříme vektor
VB→ = αVR→ + βVS→,
kde α≥ 0 a β≥ 0. Bod B ale také leží na úsečce mezi body
Ri a Si, proto platí, že VB→ = wVRi→ + (1-w)VSi→. Vztahy pro jednotlivé bázové vektory pak můžeme zkoumat zvlášť:
Ve dvourozměrném vektorovém prostoru s bází tvořenou vektory
VR→ a VS→ si také vyjádříme vektor
VB→ = αVR→ + βVS→,
kde α≥ 0 a β≥ 0. Bod B ale také leží na úsečce mezi body
Ri a Si, proto platí, že VB→ = wVRi→ + (1-w)VSi→. Vztahy pro jednotlivé bázové vektory pak můžeme zkoumat zvlášť:
| 1-w |
| qi |
| α |
| qi |
1 -
| ||
| qi |
| 2 |
| i |
| 2 |
| i |
Kvadratická rovnice pro qi pak má nanejvýš dvě reálná řešení, takže existují nanejvýš dvě různé přímky p pro zadaný úhel, obsah S a bod B, které splňují definici.
Z tohoto lemmatu tedy vyplývá, že každým bodem uvnitř mnohoúhelníka prochází pro každou dvojici hran nanejvýš dvě dělící příčky mezi těmito hranami. A protože hran je konečný počet, tak i dělících příček procházejících libovolným zvoleným bodem je nanejvýš konečně mnoho.
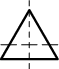 Takový důkaz naštěstí nebylo třeba provádět. Stačilo si totiž uvědomit, kde
leží nejkratší dělící příčka v rovnostranném trojúhelníku! Ani ta totiž neprochází těžištěm.
Není to totiž těžnice/výška, jejíž délka je
Takový důkaz naštěstí nebylo třeba provádět. Stačilo si totiž uvědomit, kde
leží nejkratší dělící příčka v rovnostranném trojúhelníku! Ani ta totiž neprochází těžištěm.
Není to totiž těžnice/výška, jejíž délka je | a√3 |
| 2 |
| a |
| √2 |
 31-1-6 Hroznýšovo okno (Zadání) (Řešení)
31-1-6 Hroznýšovo okno (Zadání) (Řešení)
To tak přijde QA inženýr do hospody, objedná si jedno pivo, dvě piva, nula piv, 9 999 999 piv, -1 pivo, ještěrku, xyzzy … První normální zákazník vejde do hospody, poprosí o jídelní lístek, hospoda vzplane jasným plamenem a všichni uhoří. (Zdroj: Twitter)
Takový tester navštívil váš kód a zjistil, že zhusta funguje. Sice občas spadne, když zmáčknete nějaké tlačítko, u kterého jste to na začátku nečekali, to by GUI dělat nemělo, ale jinak v zásadě dělá, co má. To je moc fajn!
První úkol se ukázal jako velmi jednoduchý, neboť jej splnil prakticky každý. Někdo využil pojmenovanou funkci, jiný lambda funkci.
Druhý úkol byl přidat tlačítko Stop, které časovač zastaví. To bylo taky celkem bezproblémové.
Nikde nebylo specifikováno, jestli se po zastavení má ještě aktualizovat čas, proto to také řada
z vás neudělala, což je v pořádku. Mělo by ale aspoň nespadnout, když jej zmáčknete a časovač zatím ještě neběží;
za takové opomenutí jste přišli o bod. Jedno z rozumných řešení bylo inicializovat časovač
(self.timer = QTimer()) už v konstruktoru.
Třetí úkol se nakonec ukázal, že nebude činit větší problémy. Stejně jako ve druhém úkolu se vyskytovaly potíže s neexistencí časovače, pokud jsem si chtěla nastavit nejdřív délku intervalu a pak teprve časovač spustit (za to byl mínus bod). Někteří z vás interval násobili a dělili 2, jiní přičítali a odčítali zvolenou konstantu (třeba 100 milisekund), což bylo obojí zcela v pořádku.
Tiše jsem pro tento úkol ignorovala, když program při změně intervalu zahazoval délku předchozího ještě nedoběhlého intervalu, neboť to přisuzuji snaze vecpat do jednoho programu řešení všech tří úkolů. Stejně tak jsem neřešila případ, kdy jste nevypisovali čas, ale počet tiků časovače od začátku programu.
Ve čtvrtém úkolu ale program zhusta nefungoval dle zadání. Dá se to otestovat třeba tak, že spustíte časovač, vyskáčete s limitem na nějakou dlouhou hodnotu (třeba 32 sekund), počkáte těsně před konec lhůty a rychle oklikáte mínus, takže se dostanete třeba na jednu sekundu, než skončí ten původní limit 32 sekund.
Co se vlastně má stát? Toť zajímavá otázka. Stále té věci chceme říkat stopky, takže by bylo fajn, kdyby po nějaké dlouhé době, ať už budeme mezitím klikat jakkoliv zběsile na aktualizační tlačítka, zobrazoval reálný čas od spuštění do poslední aktualizace. Takže za nějakou dobu by měl čas aktualizovat a nenechat se zmást změnou intervalu.
Rozhodně se ale nemá stát tohle:
- po doběhnutí 32 sekund se zobrazený čas zvedne jen o 1 s (protože tahle hodnota je nastavená v době, kdy časovač doběhl);
- po kliknutí na snižovací/zvyšovací tlačítko se restartuje časovač bez toho, aby program vzal v úvahu již uplynulý čas od posledního tiku.
Takové chování programu jsem za správné řešení úkolu 4 nepovažovala. Někteří spoléhali na to, že
metoda setInterval objektu QTimer to celé vyřeší, to tak ovšem
není. V dokumentaci asi nikde není explicitně napsané, co se vlastně stane, když změníte
interval za běhu časovače; zdá se však, že se tím nastaví čas od teď do
vypršení časovače, což ale nechceme – zahodili bychom si tím předchozí uběhlý
čas. To ostatně potvrzuje i testovací program, přinejmenším na mém stroji.