Třetí série třicátého druhého ročníku KSP
Celý leták v PDF.
Velikonoční hrošík letos přináší bohatou pomlázku: kromě zadání 4. série a komentářů k 2. sérii (ty se zdržely někde cestou), vydáváme i vzorová řešení 3. série. Ta naopak komentáře mít nebude.
Vzorová řešení 3. dílu seriálu se objeví až později, termín na jeho odevzdání je totiž prodloužený až do konce dubna. Tím pádem i výsledková listina na webu je provizorní.
Pěkné Velikonoce přejí všichni organizátoři.
Řešení úloh
- 32-3-1: Zkrat
- 32-3-2: Hledání konstelace
- 32-3-3: Kontejnerové počty
- 32-3-4: Zmatek v konektorech
- 32-3-5: Energetická náročnost
- 32-3-6: Jízdní řády
 32-3-1 Zkrat (Zadání)
32-3-1 Zkrat (Zadání)
Pojďme si první přeformulovat zadání. Dostaneme graf (energetickou síť) a v něm dva označené vrcholy (místo zkratu a centrální počítač). Našim cílem pak je rozdělit graf na dvě komponenty souvislosti odstraněním minimálního počtu hran.
Odstraňování hran a rozklad souvislého grafu na komponenty napovídá na grafový koncept zvaný hranový řez. To je množina hran taková, že po jejím odstranění se graf rozpadne na více komponent. Takovým řezem může být například množina všech hran. Když totiž z grafu odstraníme hrany úplně všechny, zbude nám spousta jednovrcholových grafů. Zajímavější otázkou ale je, kolik nejméně hran může v grafu tvořit řez? Jak velký je minimální řez?
Úloha nám zadává, že právě takový minimální řez rozdělující dva zadané vrcholy máme najít. Jak to ale udělat?
K postupu mohlo napovědět, že jde o kuchařkovou úlohu a aktuálním tématem jsou toky v sítích. Takže to by mohlo nějak souviset, ne? Pojďme tedy z našeho grafu udělat pořádnou tokovou síť. Náš graf je neohodnocený a neorientovaný. To ale není problém, upravíme ho tak, že každá hrana má kapacitu jedna. Orientaci přidáme rozdělením hran na dvě protisměrné. Uvažujme tedy nadále o grafu jako o ohodnoceném orientovaném. Také máme dva významné vrcholy, v tocích máme zdroj a stok. Tak nechť je vrchol zkratu zdroj a centrální počítač stok. To nám dává kompletní tokovou síť a na ní můžeme algoritmy z kuchařky najít maximální tok. Tak použijme například Ford-Fulkersonův algoritmus. Máme tedy tok, ale co s ním?
Pomůže nám tvrzení, že maximální tok má stejnou velikost jako minimální řez. Proč by to mělo platit? Když si představíme tokovou síť jako soustavu různě tlustých trubek a maximální tok jako objem kapaliny, který trubkami dokážeme za jednotku času protlačit). Minimální řez je v této analogii jakýmsi úzkým hrdlem. Je to označení několika trubek, které mají dohromady minimální kapacitu, jsou v součtu nejmenší, a přitom rozdělují soustavu trubek na dvě části. Z tohoto pohledu vypadá zřejmé, že maximální tok bude limitován právě tímto místem. A protože je to minimální úzké hrdlo, není žádné užší a maximální tok nebude ani menší. Z tvrzení nám tedy plyne, že pomocí toků dokážeme zjistit, kolik hran náš řez obsahuje. (Pozn.: Výše popsaná analogie není důkaz, ale pro naše potřeby stačí. Pro formality můžete nahlédnout do Průvodce labyrintem algoritmů.)
Již dříve zmíněný Ford-Fulkersonův algoritmus zkráceně funguje tak, že hledá zlepšující (neboli nenasycenou) cestu a když takovou najde, tak ji vylepší. Opakuje, dokud to jde. Právě situace na konci běhu algoritmu můžeme využít.
Když necháme algoritmus najít tok a pak spustíme hledání nenasycené cesty ze zdroje do stoku znovu, žádnou logicky nenajdeme. Když si ale uložíme všechny hrany, které nenasycenou cestu přerušili, dostaneme hrany našeho minimálního řezu. Jak jsme si totiž dříve ukázali, hrany minimálního řezu jsou plně využívány maximálním tokem. Nemůžou tedy být součástí zlepšující cesty. A protože řez rozděluje graf na komponenty, blokují jeho hrany všechny nenasycené cesty.
Takže si to shrňme:
- Energetickou síť si představíme jako tokovou síť.
- Najdeme maximální tok.
- Dalším hledáním nenasycených cest pomocí BFS najdeme hrany minimálního řezu.
Jak je to se složitostí? Nechť v je počet vrcholů, e je počet hran. Transformaci grafu uděláme lineárně s e. Maximální tok pomocí Ford-Fulkersona v grafu ohodnoceném jednotkovými kapacitami v čase O(v ·e). Závěrečný krok je pak opět lineární, tentokrát O(v+e). Celková složitost hledání vodičů k odpojení je tedy O(v ·e).
 32-3-2 Hledání konstelace (Zadání)
32-3-2 Hledání konstelace (Zadání)
Mějme posloupnost d1, d2, …, dn, o které máme zjistit, zda odpovídá stupňům vrcholů nějakého neorientovaného grafu na n vrcholech. Nejprve provedeme triviální kontroly: pokud pro nějaké i máme di<0 nebo di≥ n, pak je odpověď evidentně ne. To jistě zvládneme v čase O(n).
Pak posloupnost setřídíme, aby platilo d1 ≤ … ≤ dn. Jelikož všechna čísla di jsou malá a celá, půjde to také v čase O(n). Třeba počítacím tříděním: pořídíme si n počítadel C[0],… ,C[n-1]. Zpočátku budou nulová, pak pro každé i zvýšíme C[di] o 1. Teď tedy víme, kolikrát se vyskytl který stupeň vrcholu. Podle toho vytvoříme novou setříděnou posloupnost: zapíšeme C[0] nul, C[1] jedniček, …, až C[n-1]-krát n-1.
Teď přijde na řadu věta o skóre zmíněná v zadání. Odebereme z posloupnosti nejvyšší stupeň dn. A tolik předchozích stupňů snížíme o 1. Pokud by nám stupně došly nebo se některý z nich dostal pod 0, opět skončíme s odpovědí ne.
Tento postup opakujeme, dokud nesmažeme všechny prvky posloupnosti. Pokud jsme se dostali až tam, odpovíme ano.
Problém ovšem je, že při opakovaném používání věty o skóre se může setřídění posloupnosti stupňů rozbít. Představte si třeba posloupnost 1, 1, 2, 2. Po odtrhnutí poslední dvojky dostaneme posloupnost 1, 0, 1 a kdybychom bezhlavě pokračovali dál, příštím krokem získáme 1, -1 a odpovíme ne. To je ovšem chyba, protože původní posloupnost odpovídá cestě se čtyřmi vrcholy.
Třídit posloupnost pokaždé znova by zase bylo pomalé, takže ji musíme nějak chytře dotřiďovat. Popíšeme způsob, ke kterému nás inspiroval Jirka Kalvoda.
Představme si nějaký úsek posloupnosti, ve kterém snižujeme stupně o 1. Tento úsek leží na konci (je to suffix) a zatím byl setříděný, takže i po snížení zůstane setříděný. Jediné, co se může pokazit, je, že nejmenší stupeň v úseku (říkejme mu δ) se vyskytne i těsně před úsekem. To bylo vidět v předchozím případu: snižovali jsme úsek 1, 2, před kterým byla ještě jedna 1.
Pomůžeme si tak, že máme-li ze všech výskytů stupně δ snížit posledních k, snížíme místo toho prvních k. Tím dostaneme tatáž čísla, ale v setříděném pořadí: nejprve k-krát δ-1 (což může napojit na předchozí hodnoty δ-1), pak několikrát δ.
Abychom to mohli provést rychle, budeme si pro každý stupeň x pamatovat pozici jeho nejlevějšího výskytu (v poli indexovaném stupněm). Ukážeme, jak tyto hodnoty snadno udržovat.
Při počátečním třídění si zapamatujeme nejlevější výskyt každého stupně. Kdykoliv použijeme větu o skóre, budeme procházet posloupnost stupňů od konce po souvislých úsecích stejných stupňů (díky nejlevějším výskytům víme, jak jsou tyto úseky dlouhé). Nechť zbývá snížit k stupňů a zrovna jsme v úseku ℓ opakování nějakého stupně δ. Rozlišíme případy:
- Pokud je k > ℓ, snížíme celý úsek na δ-1 a nastavíme nejlevější výskyt hodnoty δ-1 na začátek úseku. (Jelikož snižování bude ještě pokračovat, žádné další δ-1 nalevo od úseku nebudou.)
- Pokud je k = ℓ, oproti předchozímu případu musíme navíc ohlídat, zda se úsek nenapojil na předchozí. Je-li těsně před úsekem také δ-1, její nejlevější výskyt neměníme.
- Konečně pokud k < ℓ, snížíme prvních k stupňů v našem úseku. Snížené hodnoty se opět mohou napojit na předchozí úsek; pokud nenapojí, nastavíme nový nejlevější výskyt δ-1 na začátek úseku. A stupeň δ se nejlevěji vyskytuje v našem úseku.
Všech k snížení jsme tedy zvládli v čase O(k) = O(dn). Celý algoritmus tudíž běží v čase O(n + ∑i di). Pokud graf existuje, je ∑i di rovno dvojnásobku počtu hran m (každá hrana má dva konce, proto k součtu stupňů přispěje dvojkou). Algoritmus má proto složitost O(n+m), jak požadovalo zadání. Dodejme ještě, že algoritmus by šlo snadno upravit, aby ve stejném čase graf s danými stupni sestrojil.
Rychlejší řešení: Intervalové stromy
Jelikož součet stupňů může být až Θ(n2) (představte si úplný graf), popsané řešení je až kvadratické ve velikosti vstupu. Pojďme se zamyslet, jak by se dalo zrychlit. (Z představy explicitního sestrojení grafu nicméně musíme slevit.)
Pomohou nám intervalové stromy s línými aktualizacemi, které jsou popsané třeba v kuchařce nebo v kapitole 4.5 knížky Průvodce labyrintem algoritmů. Takový intervalový strom umí udržovat nějakou posloupnost d1, …, dn a provádět nad ní tyto operace v čase O(log n):
- Pro dané i zjisti di.
- V daném úseku di, di+1, …, dj přičti ke všem hodnotám nějaké x.
- Pro danou hodnotu x najdi nejlevější prvek menší nebo rovný x (na to si stačí pro každý podstrom pamatovat minimum z hodnot v listech; detaily zkuste domyslet). Speciálně si všimněte, že touto operací umíme nahradit pamatování si nejlevějších výskytů.
Ukážeme, jak v předchozím algoritmu jedno použití věty o skóre provést pomocí O(1) operací s intervalovým stromem. Jelikož větu použijeme O(n)-krát, poběží celý algoritmus v čase O(n log n).
Nechť v posloupnosti zbyly stupně d1, …, dt (ostatní prvky dt+1, …, dn ve stromu ponecháme, jen se na ně už nikdy nebudeme ptát). Chceme tedy odstranit stupeň dt (stačí snížit t o 1) a pak snížit stupně v úseku od pozice i=t-dt do j=t-1 o jedničku. Kdyby bylo di-1 < di, stačilo by úsek od i do j snížit a posloupnost by zůstala setříděná.
Pokud di-1 = di, musíme zachovat setřídění snížením nějakých levějších výskytů tohoto stupně. Nejprve spočítáme, kolik jich je. Dotazem na intervalový strom zjistíme, kde je nejlevější výskyt stupně většího než di. To nám řekne, kolik di-ček chceme snížit. Pak si necháme najít nejlevější výskyt di. Od něj doprava budeme snižovat di-čka. A nakonec necháme snížit zbytek našeho úseku.
Ještě rychlejší řešení: Erdősova-Gallaiova věta
Jde to ale ještě rychleji, pokud použijeme pokročilejší větu o charakterizaci skóre. Dokázali ji v roce 1960 Paul Erdős (Je to maďarské jméno, takže ő čteme jako dlouhé přehlasované o a s čteme jako š.) a Tibor Gallai. Říká následující:
Věta: Posloupnost d1≥ … ≥ dn popisuje stupně nějakého grafu, pokud d1 + … + dn je sudé a navíc pro každé k od 1 do n platí:
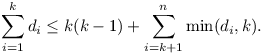
| n |
| i=1 |
Kdykoliv k zvýšíme o 1, nalevo přibude další di do sumy. Člen k(k-1) spočítáme znovu. Z pravé sumy jeden člen zmizí a ostatní členy se mohou zvýšit, pokud byly předtím omezené hodnotou k. To nastává, pokud di = k+1. Všechna taková di ale tvoří souvislý úsek a ten můžeme najít třeba tak, že si opět při třídění zapamatujeme nejlevější výskyt každé hodnoty (dokonce ani nemusíme projít hodnoty v úseku, stačí vědět, jak je úsek dlouhý).
Jedno zvýšení k nás tedy stojí konstantní čas a všechna dohromady zpracujeme v O(n).
Důkaz věty

 Sluší se ovšem větu dokázat. Původní důkaz od Erdőse a Gallaie je docela
komplikovaný (a maďarsky), my vám ukážeme jednodušší důkaz od Tripathiho,
Venugopalana a Westa z roku 2009. I tak je docela pracný.
Sluší se ovšem větu dokázat. Původní důkaz od Erdőse a Gallaie je docela
komplikovaný (a maďarsky), my vám ukážeme jednodušší důkaz od Tripathiho,
Venugopalana a Westa z roku 2009. I tak je docela pracný.
Nejprve dokážeme snazší implikaci: Pokud graf existuje, posloupnost splňuje požadavky věty. Jak už víme, součet stupňů je roven dvojnásobku počtu hran, takže to určitě je sudé číslo. Nyní uvažme jakékoliv k. Podívejme se na prvních k vrcholů (to jsou ty se stupni d1,… ,dk). Levá strana nerovnosti počítá konce hran, které se těchto vrcholů dotýkají.
Pravá strana rozebírá všechny možnosti, jak tyto hrany mohou vést. Hrany vedoucí mezi prvními k vrcholy mohou mít nejvýše k(k-1) konců (z každého vrcholu může vést hrana do každého jiného). Z každého zbývajícího vrcholu může do prvních k vést nejvýše tolik konců, kolik je stupeň vrcholu, ale ne víc než k.
Opačná implikace dá víc práce. Dostaneme nějakou posloupnost stupňů splňující podmínky věty a máme vyrobit příslušný graf. Začneme n vrcholy očíslovanými od 1 do n a prázdnou množinou hran. Postupně budeme graf upravovat tak, aby se blížil zadaným stupňům. Přitom budeme dodržovat následující pravidla:
- Pro každý vrchol i platí, že deg(i) ≤ di, kde deg(i) je aktuální stupeň vrcholu i.
- Pokud ještě existují vrcholy, pro které je deg(i) < di, nazveme r nejlevější takový. [Jelikož vrcholy označujeme čísly, znamená „i je vlevo od j“ prostě i<j.]
- Tedy vrcholy 1,… ,r-1 už mají správné stupně, pro vrchol r víme deg(r) < dr, napravo od r stupně mohou, ale nemusí být správné.
- Neexistují žádné hrany, které by měly oba konce napravo od r.
Ukážeme, jak deficit dr - deg(r) snížit, aniž bychom tato pravidla porušili. Po konečně mnoha opakováních klesne deficit na 0, takže další vrchol získá správný stupeň a r se zvýší. A po dalších dostatečně mnoha opakováních získají správné stupně všechny vrcholy a budeme hotovi.
Rozebereme postupně několik případů:
- Existuje vrchol i, pro který je deg(i) < di a není spojen hranou s r.
Vrchol i tedy musí ležet napravo od r. Tehdy přidáme hranu ri. Tím se zvýšil
deg(i) o 1, takže deficit vrcholu r klesl o 1.
K jednotlivým případům budeme kreslit obrázky. Plné čáry budou znázorňovat hrany, čárkované povedou tam, kde hrana určitě není. Pokud přes hranu nakreslíme křížek, chceme ji zrušit. A puntík přes chybějící hranu naopak znamená, že chceme hranu přidat. První případ tedy odpovídá tomuto obrázku:

- Existuje vrchol i nalevo od r, který není spojen s r. Jelikož deg(i) = di
(to platí všude nalevo) a di ≥ dr > deg(r), má vrchol i víc sousedů než r,
takže musí existovat nějaký vrchol u, který je spojen s i, ale ne s r. (Je nám
jedno, zda u leží nalevo nebo napravo od r.)
Rozlišíme podpřípady:
- Deficit vrcholu r je aspoň 2. Tehdy smažeme hranu ui a přidáme hrany
ur a ir. Tím jsme deg(u) a deg(i) zachovali a deg(r) zvýšili o 2,
tím pádem deficit r klesl o 2.

- Deficit vrcholu r je přesně 1. Jelikož součet stupňů je sudý a součet
všech di je také sudý, musí být součet deficitů také sudý. Takže když r
má lichý deficit, musí existovat ještě nějaký jiný vrchol s lichým, tím
pádem nenulovým deficitem. Tím pádem pro nějaké k napravo od r máme
deg(k) < dk. Pokud nenastal případ 1), v grafu existuje hrana rk.
Můžeme tedy smazat hrany ui a rk a přidat ur a ir. Tím se deg(u) ani
deg(i) nezmění, deg(r) zvýší o 1 a deg(k) sníží o 1. Takže
deficit r klesl o 1.

- Deficit vrcholu r je aspoň 2. Tehdy smažeme hranu ui a přidáme hrany
ur a ir. Tím jsme deg(u) a deg(i) zachovali a deg(r) zvýšili o 2,
tím pádem deficit r klesl o 2.
- Nenastal předchozí případ, takže všechny vrcholy nalevo od r jsou spojené s r.
Navíc existuje nějaký vrchol k napravo od r, pro který deg(k) ≠ min(r,dk).
Z podmínky a) víme, že deg(k) ≤ dk. Díky podmínce d) musí všechny hrany z k vést
(neostře) nalevo od r, takže deg(k) ≤ r. Kombinací všech těchto podmínek na deg(k)
získáme deg(k) < r a současně deg(k) < dk.
Jelikož nenastal případ 1), v grafu existuje hrana rk. Ovšem deg(k) < r, takže pro nějaké i nalevo od r musí chybět hrana ik. Díky nerovnostem deg(i) = di ≥ dr > deg(r) existuje nějaký soused u vrcholu i, který není sousedem vrcholu r.
V této situaci smažeme hranu ui a přidáme hrany ur a ik. Nyní deg(u) a deg(i) zůstaly zachovány a deg(r) a deg(k) se zvýšily o 1. I v tomto případě jsme tedy snížili deficit vrcholu r a nic nepokazili.

- Opět jsou všechny vrcholy nalevo od r spojené s r a mezi nějakými dvěma vrcholy i
a j nalevo od r nevede hrana. Bez újmy na obecnosti je i nalevo od j. Proto platí
di ≥ dj ≥ dr. Jelikož i a j už mají správné stupně a r nikoliv, plyne
z toho deg(i) ≥ deg(j) > deg(r). Tím pádem existuje vrchol u, který je sousedem i,
ale není sousedem r. A také vrchol w, soused j, ale nikoliv r (není vyloučeno,
že u=w). Pokud nenastal případ 2), musí u a w ležet napravo od r.
Tuto situaci vyřešíme smazáním hran ui a wj a přidáním ij a ur. Stupně deg(u), deg(i) a deg(j) se nezměnily, deg(w) klesl o 1 a deg(r) vzrostl o 1. Tím jsme opět snížili deficit vrcholu r a nic nepokazili.

A co když nenastal žádný z předchozích případů? Tehdy víme, že vrcholy 1 až r tvoří úplný graf a pro každý vrchol i napravo od r platí deg(i) = min(r,di). Jelikož podle podmínky d) není žádná hrana celá vpravo od r, platí pro počet všech konců hran:
| n |
| i=1 |
| n |
| i=r+1 |
To připomíná nerovnost z tvrzení věty (r zde hraje roli k z věty). Pravá strana je stejná, nalevo byla ve větě suma všech di. Dostaneme tedy:
| n |
| i=1 |
| n |
| i=1 |
Jenže podle podmínky a) platí pro všechna i také di ≥ deg(i). Obojí současně může platit jenom tehdy, když di = deg(i) pro všechna i, takže každý vrchol už má požadovaný stupeň. Hotovo, důkaz je u konce.
Dodejme ještě, že náš důkaz je vlastně algoritmický: říká nám, jak graf s požadovanými stupni sestrojit. Efektivní implementaci nicméně už domýšlet nebudeme.
 32-3-3 Kontejnerové počty (Zadání)
32-3-3 Kontejnerové počty (Zadání)
Úlohu vyřešíme ve 2D, pak se postup snadno zobecní do 3D.
Kdybychom nemuseli mít celočíselné rozměry krabic, nevyhovující rozměry krabic obecně budou tvořit nějakou souvislou podmnožinu [0,k]2 obsahující (0,0), ta bude navíc symetrická podle přímky { (x,y) ∈R2 | x = y }.
Z této představy mimo jiné vidíme, proč nemusí existovat z hlediska inkluze minimální krabice, která dokáže věci všechny obsáhnout. Uvažme například čtvrt kružnice se středem v (0,0) a poloměrem 10. (Nechť je tedy předmět úsečka délku 10). Krabice s rozměry 8×6 a 9×5 věci obsáhnou, ale nejsou v inkluzi a žádná krabice, jež by měla rozměry menší než obě krabice zároveň neexistuje.
Vraťme se však k popisu algoritmu. Budeme si udržovat interval, do něhož budou nutně patřit oba rozměry všech zbývajících vyhovujících krabic. Na začátku to bude [1, k].
Položme jeden rozměr roven x=k, druhý y=1. Následně budeme opakovat následující dokud x ≥ y . Zeptejme se na tuto krabici s rozměry x ×y. Pokud se věci vejdou, zmenšíme x o 1, jinak zvětšíme y o 1.
Dozvěděli jsme se, jaké je minimální vyhovující y k danému x pro x ≥ y, pokud platí opačná nerovnost, ze symetrie prohodíme rozměry.
Snadno nahlédneme, že dotazů položíme k+O(1).
| x+y |
| 2 |
| x+y |
| 2 |
| x+y |
| 2 |
Z těchto dotazů budeme opět schopni zjistit všechny vyhovující krabice.
| k |
| i=1 |
Nyní ukážeme, že je v nejhorším případě nutné položit alespoň k2/4 + O(k) dotazů. Uvažme věci, které jdou do krabice zabalit, právě když je součet délek jejich stran alespoň nějaké fixní s. Uvažme množinu rozměrů krabic M1 = { (x1, x2, x3) | x1 + x2 + x3 = s, xi ≤ k, x1 > x2 > x3 }. Abychom zjistili množinu vyhovujících krabic musíme se zeptat na každou z krabic s rozměry v M1. (Kvůli možným rotacím případně se stačí na 1 ze všech krabic jejichž rozměry jsou pouze zpermutované.)
Toto je jasné, protože všechny vzhledem k inkluzi menší krabice nevyhovují, naopak všechny větší krabice vyhovují. Proto nelze z ničeho odvodit, jestli taková krabice vyhovuje. Zda je krabice s rozměry v M použitelná, není tedy možné odvodit z použitelnosti jiných krabic a musíme se na ni skutečně zeptat.
Podobně se musíme zeptat i na všechny kombinace rozměrů se součtem s - 1 (množinu M2), všechny ostře větší krabice splňují, ostře menší krabice nesplňují.
Z počtu prvků v M1 a M2 plyne odhad. Volbou s = 3/2 ·k dostaneme velikost M1 ∪M2 asymptoticky ≈ k2 / 4. Platí |M1| ≈ |M2| a pro konkrétní x existuje totiž k - |x - k/2| bodů ve se součtem souřadnic s. Součtem přes všechny možné x a podělením 3! kvůli symetrii dostaneme součet.
 32-3-4 Zmatek v konektorech (Zadání)
32-3-4 Zmatek v konektorech (Zadání)
Ke každé koncovce dostaneme právě dva vyhovující konektory. Pojďme se zamyslet, jak nám pomůže představovat si koncovky jako hrany a konektory jako vrcholy grafu. Pokud všechny hrany zorientujeme tak, aby vstupní stupeň žádného vrcholu nepřesáhl 1, úlohu vyřešíme (orientace hrany směrem k vrcholu značí zapojení příslušné koncovky do příslušného konektoru).
Nejprve se zbavme listů, tedy vrcholů stupně 1. Přilehlé hrany určitě můžeme zorientovat směrem k listům, jinak by jim prostě zůstal nulový vstupní stupeň. Každý list pak můžeme i s příslušnou hranou z grafu odebrat a pokračovat dál. Získáme-li tímto postupem nějaký izolovaný vrchol, můžeme ho jednoduše rovnou taky odstranit.
Tímto postupem buď úlohu přímo vyřešíme, nebo získáme graf, kde má každý vrchol stupeň aspoň 2. Hrana přitom sousedí se dvěma vrcholy, tedy aby šla úloha vůbec vyřešit, musí být všechny stupně rovny právě 2, protože jinak máme víc hran než vrcholů a tedy víc koncovek než konektorů.
Teď už je to snadné. Stupně ověříme a zjistíme, zda lze úlohu řešit. Pokud ano, pracujeme s disjunktními cykly. A jejich hrany už triviálně zorientujeme libovolným směrem v rámci každého cyklu. Získali jsme tak jednoduchý lineární algoritmus.
Snadno nás taky mohlo napadnout řešit úlohu přes toky v sítích, neboli podobně jako se typicky hledá maximální párování. Použitím Dinicova algoritmu bychom si však časově pohoršili na O(N3/2), kde N je počet zadaných koncovek.
 32-3-5 Energetická náročnost (Zadání)
32-3-5 Energetická náročnost (Zadání)
Síť satelitů nadále budeme uvažovat jako strom s ohodnocenými hranami.
Vezmeme libovolnou hranu e s cenou ce. Bude nás zajímat, kolik zpráv přes ni projde. Každý vrchol na ní musí poslat svou zprávu všem vrcholům na druhé straně. Graf se po odebrání této hrany rozpadne na 2 stromy T1 a T2. Cena přenosu zpráv přes e bude dohromady ce ·|T1| ·|T2| .
Výsledná cena bude součtem přes všechny hrany. Zbývá určit kolik vrcholů leží na každé straně každé hrany. Toto umíme spočítat efektivně od listů.
Udržujme si zásobník listů, zpočátku obsahující listy původního stromu. Všem vrcholům ještě nastavíme multiplicitu na 1. Pak postupně zpracováváme listy z vrcholu zásobníku. Chystáme se odebrat L, mající jediného zbývajícího souseda I. Odebereme z grafu L a hranu s ním incidentní. Pak I připočteme multiplicitu L. Pokud se I stal listem, přidáme ho do zásobníku.
Nahlédneme, že multiplicita L při odebírání určuje počet vrcholů na jedné straně hrany spojující I a L. Tím pádem umíme dopočíst počet vrcholů na opačné straně hrany. Při odebírání L máme tedy dost informací k určení celkové ceny přenosu přes hranu mezi I a L, čili ji můžeme v tomto okamžiku zaúčtovat.
Nakonec zůstane v grafu jeden vrchol a všechny hrany tak budou zaúčtovány. Takto jsme získali lineární řešení.
 32-3-6 Jízdní řády (Zadání)
32-3-6 Jízdní řády (Zadání)
Ukázalo se, že se nám podařilo zadat seriál o dost obtížnější, než jsme zamýšleli. Za to se všem řešitelům omlouvám. Nakonec přišlo jediné řešení, a to od Jirky Kalvody, kterému tímto gratulujeme k zisku 18 bodů z 15 (některé věci vyřešil lépe než původně zamýšlené autorské řešení).
Po delším úsilí jsem došel k závěřu, že neumím napsat vzorové řešení, které by bylo dostatečně jednoduché a pro většinu řešitelů srozumitelné a zároveň dávalo rozumné výsledky. Nakonec jsme se tedy rozhodli vzorové řešení nevydávat. Pokud by vás zajímalo, jak se některé úkoly daly řešit, klidně mi napište.