Třetí série začátečnické kategorie třicátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

• 30-Z3-1: Rozkolísaná produktivita
• 30-Z3-2: Podlézání Číňanům
• 30-Z3-3: Teambuilding
• 30-Z3-4: Korporátní seznamka
• 30-Z3-5: Schůze vedoucích
• 30-Z3-6: Těžce zasloužená dovolená

30-Z3-1 Rozkolísaná produktivita (Zadání)

Dostali jsme za úkol najít v seznamu n čísel dva prvky a, b takové, že druhá mocnina jejich rozdílu ((a-b)²) je největší.

Jako první potřebujeme načíst vstup a vytvořit z něj seznam čísel. Jak na to, si můžete přečíst v naší encyklopedii, kde najdete i následující zaklínadlo pro načtení seznamu čísel oddělených mezerou:

pole = list(map(int, input().split()))

O jeho významu teď nemusíte příliš hloubat (nechcete-li), vyzkoušejte si, že funguje (např. tak, že si načtené pole vypíšete příkazem print(pole)).

Pomalé řešení

Triviální řešení by spočívalo v tom pocitvě vyzkoušet všechny dvojice, pro každou spočítat (a-b)² a zapamatovat si největší výsledek a pro kterou dvojici nastal.

Jak takovou věc udělat? Použijeme dva vnořené for cykly, které budou procházet rozsah 0 až N-1. Když to uděláme, tělo vnitřního cyklu se spustí jednou pro každou možnou dvojici prvků. Vyzkoušejme si to (do těla cyklu přidáme ladící výpis, abychom viděli, co se děje):

pole = [25, 77, 12]
for i in range(len(pole)):
  for j in range(len(pole)):
    print(i, j, pole[i], pole[j])

0 0 25 25
0 1 25 77
0 2 25 12
1 0 77 25
1 1 77 77
1 2 77 12
2 0 12 25
2 1 12 77
2 2 12 12

Všimněme si dvou věcí:

1. Každou dvojici navštívíme dvakrát, podruhé v opačném pořadí (např. 0 2 a 2 0). Vzhledem k tomu, že nám nezáleží na pořadí (rozmyslete si, že (b-a)² = (a-b)²), děláme zbytečně dvakrát tolik práce.
2. Zkoumáme i dvojice (a,a) (např. 1 1), které zadání nedovoluje.

Obou těchto nešvarů se můžeme snadno zbavit tak, že vnitřní smyčka bude místo od 0 do N-1 procházet jen rozsah od i+1 do N-1:

for i in range(len(pole)):
  for j in range(i+1, len(pole)):
    print(i, j, pole[i], pole[j])

0 1 25 77
0 2 25 12
1 2 77 12

Vida, ve skutečnosti máme jen tři dvojice k vyzkoušení.

Nyní stačí pro každou dvojici spočítat druhou mocninu rozdílu (v našem případě hodnotu (pole[j] - pole[i])**2). V nějaké pomocné proměnné si budeme udržovat nejvyšší zatím objevenou hodnotu takového výrazu. Pokud aktuální hodnota je větší než dosavadní maximum, nahradíme ho a zároveň si do dalších pomocných proměnných uložíme aktuální indexy i a j, pro které nové maximum nastává. Na konci programu jen vypíšeme zapamatovanou nejlepší dvojici.

Celý program by pak mohl být celkem kratičký:

N = int(input())
pole = list(map(int, input().split()))
maximum = -1
max_i = -1
max_j = -1
for i in range(N):
  for j in range(i+1, N):
    hodnota = (pole[j] - pole[i])**2
    if hodnota > maximum:
       maximum = hodnota
       max_i = i
       max_j = j
print(max_i, max_j)

Řešení má časovou složitost O(N²), protože obsahuje dva vnořené cykly s až N opakováními.

Rychlé řešení

Zkusme to rychleji. Protože o druhé mocnině se hůř přemýšlí, vyřešme si nejdřív jednodušší úlohu, kdy hledáme dvě čísla s největším rozdílem, bez mocnění.

Asi jste si někdy v hodinách matematiky říkali, že rozdíl dvou čísel lze chápat jako jejich vzdálenost na číselné ose – až na znaménko. Ale znaménka řešit nemusíme, pokud si řekneme, že vždy budeme odčítat menší číslo od většího (opačně se to zřejmě nevyplatí). Například pro vstup 5 7 -2 1 budou čísla na ose vypadat takto:

Najít na takovém obrázku dvě čísla s největším rozdílem, totiž dvě nejvzdálenější čísla, není vůbec těžké: očividně je to největší (nejpravější) a nejmenší (nejlevější) číslo – v našem případě 7 a -2, které najdeme v posloupnosti na pozicích 1 a 2. Jejich vzdálenost/rozdíl je 9.

Tedy pro řešení této zjednodušené úlohy stačí najít, kde se v posloupnosti nachází největší a nejmenší prvek a jejich pozice vypsat, číselnou osu si v programu vyrábět nemusíme.

Pozor na to, že nemůžeme použít přímo vestavěné pythoní funkce min a max, protože ty vrací pouze hodnotu minima/maxima (-2/7), nikoli pozici (2/1). Místo toho můžeme minimum/maximum najít „ručně“ for cyklem od 0 do N-1, který bude udržovat průběžné minimum/maximum a jeho pozici.

Co když ale nehledáme prvky s největším rozdílem, nýbrž s největší druhou mocninou rozdílu? Překvapivě to na řešení vůbec nic nezmění. Druhá mocnina je takzvaně rostoucí funkce – čím větší číslo (není-li záporné), tím větší jeho druhá mocnina. Tedy dvojice s největším rozdílem je zároveň dvojice s největší druhou mocninou rozdílu.

Alternativně se dá na problém dívat opět geometricky. Hodnota (a-b)² udává obsah čtverce se sousedními vrcholy v bodech a a b na číselné ose:

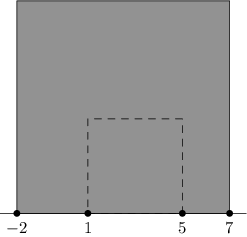
Opět si snadno rozmyslíte, že největší čtverec získáme, když za vrcholy vezmeme minimum a maximum.

K nalezení minima a maxima nám stačí jednou projít seznam, což zvládneme v lineárním čase.

Program je ještě jednodušší než ten kvadratický:

N = int(input())
pole = list(map(int, input().split()))
maximum = pole[0]
minimum = pole[0]
max_pos = 0
min_pos = 0
for i in range(len(pole)):
  if pole[i] >= maximum:
    maximum = pole[i]
    max_pos = i
  if pole[i] < minimum:
    minimum = pole[i]
    min_pos = i
print(min_pos, max_pos)

Filip Štědronský

30-Z3-2 Podlézání Číňanům (Zadání)

Výjimečně jsme si pro vás připravili úlohu, která vlastně není ničím zákeřná. Vyrobit palindrom ze slova na vstupu totiž není vůbec těžké, jak dokazuje i poměrně vysoký počet z vás, kteří úlohu vyřešili na plný počet bodů.

Aby byl řetězec délky N palindromem, musí být znaky na indexech i a N - i - 1 pro 0 ≤ i < N stejné. Jinou podmínku ale nemáme a speciálně se nijak vzájemně neovlivňují znaky, které jsou na jiných pozicích. Ať chceme nebo ne, musíme tuto podmínku splnit pro každé i. Podíváme se tedy na každou dvojici. Pokud už se znaky shodují, není co řešit. V opačném případě však nezbude než alespoň jeden z nich změnit. Ani nemusíme příliš přemýšlet, aby bylo jasné, že stačí vždy změnit pouze jeden z nich.

Tak tedy znovu. Projdeme vstupní řetězec po znacích zároveň zepředu i zezadu. Pokud se znaky liší, zvýšíme počítadlo. V každém případě ale jeden znak přiřadíme do druhého, tím nic nezkazíme. Skončit můžeme už v půlce. Rozmyslete si ale, že nezáleží na tom, jak půlku zaokrouhlíme. Nakonec vypíšeme počítadlo a změněný řetězec.

Z praktického hlediska ovšem může dojít k problémům. V některých jazycích jsou textové řetězce k nepoznání od obyčejného pole znaků (například v C), kdežto v jiných jsou nezměnitelné (včetně Pythonu). Pokud řetězec nemůžete měnit, můžete z něj pole udělat a pak jej převést zase zpět. My si ale popíšeme ještě jiné řešení.

Myšlenka je jednoduchá: vezmeme půlku vstupního textu, a vypíšeme ji. Pak přidáme prostřední znak, pokud byl na vstupu lichý počet znaků. Nakonec vypíšeme znovu první půlku, ale tentokrát pozpátku. Drobnou vadou na kráse je ale požadavek úlohy k vypsání počtu změn – ten nám ale nic nebrání spočítat původní metodou, protože v ní měnit řetězec nepotřebujeme.

S trochou magie napíšeme v Pythonu mile krátký program:

input()
s = input()
h = len(s) // 2

print(sum(s[i] != s[-1 - i] for i in range(h)))
print(s[:h + len(s) % 2] + s[h - 1::-1])

První print využívá toho, že True má hodnotu 1, zatímco False 0. Sečtením hodnot podmínek dostaneme přesně hodnotu, kterou hledáme. Druhý pak vypisuje zpalindromovaný vstup. K vyřezávání podřetězců i k obrácení řetězce používáme syntaktické pozlátko pro řez, po anglicku slice. Jedná se o mocný nástroj pro práci s objekty, které se chovají jako pole.

Pochlubte se nám třeba na fóru, jak krátké řešení jste vymysleli vy!

Ondra Hlavatý

30-Z3-3 Teambuilding (Zadání)

Máme C chodeb vycházejících paprsčitě ze společného středu. Jednotlivé chodby mají délky ℓ_i, součet délek všech chodeb označíme L. Chodby obsahují klíče, dveře a dolary. Máme D druhů klíčů, od každého druhu existují v mapě právě jedny dveře a jeden klíč. Ptáme se, kolik nejvíce dolarů jde sesbírat.

Pomalé řešení

Jak bychom úlohu řešili, kdybychom v bludišti fyzicky stáli? Třeba takto: vydáme se první chodbou, sbíráme, co potkáme. Pokud narazíme na dveře, které neumíme otevřít, vrátíme se zpátky do středu a zkusíme jinou chodbu. Můžeme například chodby zkoušet v pořadí první, druhá, třetí, …, poslední, pak zase první a tak dál.

Ještě musíme poznat, kdy skončit. Snadno si rozmyslíte, že pokud někdy projdeme všech C chodeb, aniž bychom při tom sebrali cokoliv nového, už nemá cenu procházet je znovu (dopadlo by to stejně). V takovém případě můžeme skončit.

Jak takovou věc naprogramovat? Chodby můžeme reprezentovat jako seznam seznamů (či dvojrozměrné pole) – každý z vnitřních seznamů popisuje obsah jedné chodby, v pořadí od středu ke kraji.

Jádro programu pak tvoří tři vnořené cykly:

1. while cyklus, který opakuje procházení, dokud to má cenu,
2. cyklus přes všechny chodby,
3. cyklus, který postupuje jednou chodbou, dokud to jde.

Abychom mohli vnější cyklus včas ukončit, pořídíme si jednu proměnnou udávající, jestli jsme během této iterace vnějšího cyklu sebrali něco nového. Na začátku každé iterace ji nastavíme na False, a pokud bude False i na konci, cyklus zastavíme.

Musíme si pamatovat, jaké klíče máme sebrané. K tomu můžeme použít například pole délky D, které na i-tém místě má nulu nebo jedničku podle toho, jestli už jsme sebrali klíč i-tého druhu. Pak snadno v konstantním čase zjistíme, jestli nějaký klíč máme. Pozor: kdybychom si místo toho pamatovali seznam sebraných čísel klíčů a testovali přítomnost v tomto seznamu (např. operátorem in), bude to pomalé, protože by se musel při každém testu projít celý tento seznam namísto toho, abychom se podívali jen na jedno konkrétní místo.

Také se musíme postarat o to, abychom žádnou věc nesebrali dvakrát (zvláště dolary). Snažší než zvlášť si pamatovat, co už jsme sebrali, je po sebrání prostě příslušné políčko v mapě změnit na prázdné. Pak při příštím průchodu není co sbírat.

Jak dlouho to celé bude trvat? Jeden průchod přes všechny chodby trvá O(L). Při každém průchodu musíme sebrat aspoň jeden nový klíč, jinak bychom se příště nedostali na žádná nová místa a skončili. Uděláme tedy maximálně D těchto průchodů. Odtud dostáváme celkovou časovou složitost O(LD).

Program (Python 3)

Rychlejší řešení

Proč je předchozí řešení pomalé? Tráví spoustu času tím, že znovu prochází úseky chodeb, které už v předchozím kole prošlo. Zkusme se toho vyvarovat. To zařídíme jednoduše: pro každou chodbu si budeme pamatovat, kde jsme v jejím procházení posledně skončili (v kolikátém políčku od středu). Při opakovaném prozkoumávání chodby pak budeme pokračovat od tohoto bodu namísto od začátku.

To zařídíme jednoduše: pořídíme si pole o C prvcích, kde si na i-tém místě budeme pamatovat poslední navštívenou pozici v i-té chodbě.

Tohle řešení má ještě jednu výhodu: nemusíme z mapy odstraňovat sebrané věci, protože nikdy nevstoupíme dvakrát na totéž políčko.

Jak rychlé to bude teď? Na první pohled by se mohlo zdát, že když každé políčko navštívíme nejvýše jednou, bude stačit čas O(L). Ale to není pravda. Na začátku každého kola musíme zkontrolovat všechny chodby a zjistit, ve kterých se můžeme pohnout. Tím strávíme čas až O(C) a můžeme se při tom klidně pohnout jen v jedné chodbě o jedno políčko.

Představte si například následující bludiště:

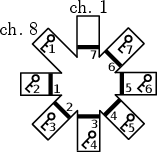
Chodby procházíme od horní po směru hodinových ručiček. Po každém obejití všech chodeb sebereme přesně jeden nový klíč a projdeme jedny nové dveře. Po každém sebrání klíče nám může trvat až O(C) najít správné dveře. Celkem tedy spotřebujeme čas O(CD) na hledání dveří a O(L) na projití všech ostatních políček (každé navštívíme nejvýše jednou). Celková časová složitost je O(L + CD).

Program (Python 3)

Ještě rychlejší řešení

Když sebereme nový klíč, potřebovali bychom umět rychle zjistit, kde k němu leží odpovídající dveře. Protože to je jediné místo, které se nám nově zpřístupnilo a kde má cenu zkoumat. To zařídíme jednoduše: pořídíme si pole délky D, kde si na i-tém místě budeme pamatovat číslo chodby, ve které leží dveře i-tého druhu (pokud jsme je již objevili; na začátku tam bude třeba -1).

Potom když objevíme nový klíč, můžeme se podívat do tohoto pole a pokračovat ve zkoumání nově odkrytých dveří ve správné chodbě bez dalšího hledání.

Výsledný program může vypadat třeba takto: pořídíme si frontu (seznam) chodeb k prohledání. Ta bude obsahovat chodby, ve kterých máme šanci objevit nějaká nová políčka. Na začátku do ní umístíme všechny chodby. Poté vždy opakujeme následující: vybereme jednu chodbu z fronty, procházíme ji od posledního navštíveného místa, kam až to jde, sbíráme věci po cestě.

Pokud se zastavíme u dveří, které neumíme otevřít, uložíme si do pomocného pole číslo chodby, ve které se nachází. Kdykoli sebereme nový klíč, podíváme se do pomocného pole a pokud v něm máme číslo chodby obsahující příslušné dveře, přidáme ji do fronty (protože se v ní zpřístupnil nový prostor, který bychom měli někdy prozkoumat).

Nyní už opravdu každé políčko navštívíme nejvýše jednou a provedeme na něm konstantní množství operací, dostáváme tedy kýženou složitost O(L). Lépe to určitě nepůjde, protože čas O(L) potřebujeme na načtení vstupu.

Program (Python 3)

Filip Štědronský

30-Z3-4 Korporátní seznamka (Zadání)

Zopakujme si zadání: Dostali jsme řetězec znaků A, B a _. Chceme na místa podtržítek vyplnit A a B tak, aby nikdy neležela tři stejná písmena vedle sebe.

Řešení rozborem případů

Nejprve ukážeme řešení založené na rozboru případů. Řetězec budeme procházet zleva doprava a postupně doplňovat písmena. Nejprve se podívejme na případy, kdy posloupnost začíná jedním nebo několika A. Označme a jejich počet:

• Pokud a>2, řešení evidentně neexistuje.
• Pokud a=2, podíváme se na následující znak:
  • Je-li to B, můžeme počáteční AA přeskočit a pokračovat ve zkoumání řetězce od B.
  • Je-li to _, musíme ho nutně změnit na B (jinak by vzniklo AAA). Pak AA přeskočíme a pokračujeme od B.
• Pokud a=1 a následuje B, opět přeskočíme A.
• Jinak za jediným A následují mezery. Rozeberme, kolik jich může být a jaký znak za nimi leží:
  • A_A: přepíšeme na ABA.
  • A__A: přepíšeme na ABBA.
  • A___A: přepíšeme na ABABA.
  • A____A: přepíšeme na ABABBA. Tento postup můžeme popsat obecně pro libovolný počet mezer: střídáme A a B, při lichém počtu mezer připíšeme na konec ještě jedno B.
  • A_B: přepíšeme na AAB.
  • A__B: přepíšeme na ABAB.
  • A___B: přepíšeme na AABAB. Obecně to vypadá tak, že střídáme B a A a při lichém počtu mezer přidáme na začátek A.
  V každém případě pokračujeme od posledního znaku zpracovaného úseku.

Všimněte si, že těmito pravidly nic nezkazíme, protože část, kterou jsme už prošli, se s tou dosud neprojitou nemůže nijak ovlivňovat. (Jedinou výjimkou je případ AA_, kdy je ovšem doplnění B vynucené.)

Podobně můžeme postupovat, pokud řetězec začíná na B. Použijeme stejná pravidla, je si v nich A s B prohodí role. Pokud by řetězec začínal mezerami, můžeme si představit, že před řetězcem leží jedno A. Tím také nic nezkazíme, protože A_… umíme vyplnit, ať už za ním následuje cokoliv. Ze stejného důvodu si za mezerami na konci vstupu můžeme domyslet libovolný znak.

Toto řešení pracuje v lineárním čase, tedy O(n) pro vstup o n znacích. Důvod je snadný: na každý znak vstupu se podíváme pouze konstanta-krát.

Program (Python 3)

Systematičtější řešení

Předchozí řešení je snadné naprogramovat, ale chvíli trvá přijít na správná pravidla. Podívejme se ještě na jiný přístup, který je sice pracnější, ale systematičtější a také obecnější. Funguje i v případech, kdy namísto tří stejných znaků zakážeme nějaký jiný počet nebo použijeme více než dvě písmena.

Řetězec budeme opět procházet zleva doprava a počítat přitom čísla X(i,j,z). Ta budou rovna 0 nebo 1 podle toho, zda je možné vyplnit prvních i znaků řetězce tak, aby končily na právě j znaků z. Pro naši úlohu je tedy i=1,… ,n, j=1,2 a z=A,B. (Například X(5,2,A)=1 znamená, že prvních 5 znaků lze vyplnit tak, aby končily na AA, před kterým bude jiné písmeno než A.)

Rozmyslíme si, podle jakých pravidel tato čísla budeme počítat. Začneme takto: Pokud je prvním znakem řetězce nějaké písmeno z, bude X(1,1,z)=1 a X(1,1,z')=0 pro všechna z'≠ z. Začíná-li řetězec podtržítkem, bude X(1,1,z)=1 pro každé z.

Nechť nyní chceme spočítat X(i,j,z) a už známe všechna X(i',j',z') pro i'<i. Všimneme si, že X(i,j,z)=1 může nastat pouze v těchto případech:

• Především na i-té pozici v řetězci musí ležet buď z nebo _.
• Je-li j>1, musí být X(i-1,j-1,z)=1 (před j-tým z-kem v řadě jich musí ležet ještě j-1).
• Je-li j=1, musí být X(i-1,j',z')=1 pro nějaké j' a z'≠ z (před prvním z-kem musí ležet nějaký jiný znak, a to libovolně-krát).

Podle těchto pravidel můžeme spočítat všechna X(i,j,z). Zvládneme to v lineárním čase: postupně zkoumáme n různých i, pro každé z nich konstantní počet j a z, a pokaždé otestujeme nejvýše konstantně různých X(i-1,j',z').

Ze spočítaných hodnot můžeme jednoduše zjistit, jestli nějaké korektní vyplnění písmenek existuje: stačí se podívat, jestli je X(n,j,z)=1 pro nějaké j a z. Tím také zjistíme, kterým znakem toto vyplnění končí a kolikrát se opakuje. Pak budeme hledat X(n-j,j',z') a z toho se dozvíme, jaké písmeno leží před tím, a tak dále, až pozpátku sestavíme celou odpověď. Zvládneme to opět v lineárním čase.

Program (Python 3)

Martin „Medvěd“ Mareš

30-Z3-5 Schůze vedoucích (Zadání)

Program (C++)

Pali Rohár

30-Z3-6 Těžce zasloužená dovolená (Zadání)

Kdyby mi dal někdo strukturu firmy nakreslenou na tabuli, tak bych postupoval asi takto: Najdu někoho, kdo nemá žádné podřízené, pokud má dost peněz na dovolenou (alespoň D), odečetl bych mu D z výdělku a udělal si čárku, že další zaměstnanec si ulil peníze. Nakonec bych jeho výdělek přičetl k výdělku jeho nadřízeného a smazal ho. Takto bych postupně smazal všechny zaměstnance a zbyl by mi jenom generální a čárky, co jsem si dělal za každé ukradení zisku.

Podobný algoritmus by se dal i naprogramovat – když budeme mít pro každého zaměstnance seznam jeho podřízených a částku jakou vydělal, můžeme celkový zisk i počet krádeží spočítat rekurzivně. Efektivně tak dojdeme dolů k lidem, kteří žádné další podřízené nemají, a když je projdeme, tak se teprve k jejich nadřízeným. Funkce nakonec vrátí dvojici čísel – čistý zisk oddělení a počet krádeží, které podřízení dohromady udělali:

def spocti(zamestnanec):
    zisk = zamestnanec.zisk
    pocet_kradezi = 0
    # posčítáme všechny podřízené
    for podrizeny in zamestnanec.podrizeni:
    	(zisk_p, kradeze_p) = spocti(podrizeny)
    	zisk += zisk_p
    	pocet_kradezi += kradeze_p

    if zisk >= D:
    	# máme zisk alespoň D, tak si nakrademe
    	pocet_kradezi += 1
    	zisk -= D
    
    return (zisk, pocet_kradezi)

Takový algoritmus projde každý vrchol právě jednou a nedělá s ním nic složitého, takže poběží v lineárním čase. Jenom bude ještě před spuštěním funkce převést formát vstupu na hierarchii, se kterou pracuje tato funkce, ale to také jistě zvládneme v lineárním čase (a paměti). Pro úplnost, implementace by mohla vypadat nějak takto:

# projdeme všechny záznamy na vstupu
for (id, nadrizeny, zisk) in vstup:
    z = zamestnanci[id]
    z.zisk = zisk
    # přidáme zaměstnance jako podřízeného
    zamestnanci[nadrizeny].podrizeni.add(z)

Rekurze nicméně v praxi může být trochu omezující, protože vám většina programovacích jazyků (třeba Python) neumožní mít moc zanořenou funkci. Takže by to mohlo při zpracování nějaké šílené korporace s mnoha vrstvami managementu spadnout. To se dá sice také vyřešit, ale bude zajímavější si ukázat jiné řešení, které rekurzi nepotřebuje.

Tentokrát při načtení vstupu nepotřebujeme sestavit celou organizační strukturu, stačí si jenom ke každému zapsat, kolik má podřízených, a referenci na nadřízeného. Pak si uděláme frontu, do které si budeme dávat lidi bez podřízených. Přečtění vstupu by tedy mohlo vypadat takto:

for (id, nadrizeny, zisk) in vstup:
    z = zamestnanci[id]
    z.zisk = zisk
    z.nadrizeny = zamestnanci[nadrizeny]
    # jenom si přičteme počet podřízených
    z.nadrizeny.podrizeni += 1

for z in zamestnanci:
    if z.podrizeni == 0:
        fronta.add(z)

Pak začneme frontu procházet a sčítat zisky. Navíc pokaždé, když vyřešíme nějakého zaměstance, tak jeho nadřízenému kromě přičtení zisku odebereme podřízeného (odečteme počítadlo) a kdyby byl poslední, tak ho přidáme do fronty ke zpracování (protože teď už má všechny podřízené smazané).

pocet_kradezi = 0
while fronta.length > 0:
    z = fronta.pop()
    if z.zisk >= D:
    	pocet_kradezi += 1
    	z.zisk -= D
    z.nadrizeny.zisk += z.zisk
    # odečteme zaměstnance z podřízených
    z.nadrizeny.podrizeni -= 1
    if z.nadrizeny.podrizeni == 0:
    	fronta.add(z.nadrizeny)

Tento algoritmus také zpracuje každého právě jednou – nikoho do fronty nedá dvakrát, protože počet podřízených pokaždé zmenší o jedna, a tak bude roven nule jenom jednou. A každý se do fronty dostane hned, když se zpracují všichni jeho podřízení, takže by mělo postupně dojít na všechny. V každé iteraci udělá jenom nějaké triviální operace, takže také poběží lineárně dlouho.

Standa Lukeš