Čtvrtá série začátečnické kategorie třicátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 30-Z4-1: Statistika sprintů
- 30-Z4-2: Klíče od tělocvičny
- 30-Z4-3: Uhlazovací válec
- 30-Z4-4: Ohrazení zahrádky
- 30-Z4-5: Sběr jablek
- 30-Z4-6: Analýza nadávek
 30-Z4-1 Statistika sprintů (Zadání)
30-Z4-1 Statistika sprintů (Zadání)
Na začátek je vhodné uvědomit si, že místo nejnižšího průměru stačí hledat nejnižší součet (sumu). To proto, že průměr k-tice čísel (a1, … , ak) je (a1 + … + ak) / k a k je kladná konstanta. Přeformulujeme tedy zadání na hledání nejnižší sumy.
Triviální řešení může vypadat takto: Spočítáme sumy pro k-tice (x0, … , xk-1), (x1, … , xk), … Sumy si budeme ukládat do pole velikost n-k a index v poli bude ukazovat první prvek k-tice. Toto pole poté projdeme a najdeme v něm minimum (průběžně si udržujeme nalezené minimum a příslušný index).
Toto řešení poběží v čase O((n-k) · k), protože (n-k)-krát sčítáme k-tici čísel. Pokud k je výrazně menší než n, můžeme výraz zjednodušit na O(nk).
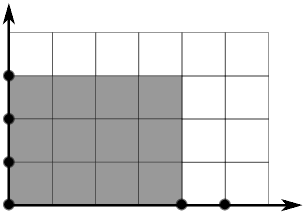
Problém triviálního řešení je v tom, že mnohokrát sčítáme stejná čísla. Obrázek níže ukazuje, jaké čtveřice sčítáme (vždy jeden obdélník přísluší jedné čtveřici). Čím tmavší pozadí, tím vícekrát se daný prvek přičte (16 se přičte ve třech čtveřicích).

Všimněme si, že když přecházíme od k-tice s indexem i ke k-tici s indexem i+1, tak jediné, v čem se suma změní, je to, že vypadne prvek i a přibude prvek i+k.
Sumy tedy nemusíme počítat pokaždé znovu: jakmile známe i-tou sumu, můžeme z ní v konstantním čase spočítat (i+1)-ní – stačí jeden prvek odečíst a jeden přičíst. Jedině pro pozici 0 stále musíme poctivě nasčítat k prvků.
Tím vylepšíme předchozí řešení na časovou složitost O(n), protože na každý prvek sáhneme maximálně dvakrát.
 30-Z4-2 Klíče od tělocvičny (Zadání)
30-Z4-2 Klíče od tělocvičny (Zadání)
Základní myšlenka je jednoduchá. Budeme chtít postupně vytvořit seznamy Si obsahující všechny členy s klíčem kvality i (pro i od 0 do K). Potom jen sečteme jejich délky a dostaneme výsledek.
S0 je prostě seznam vedoucích klubu, ten dostaneme přímo na vstupu.
Nyní bychom chtěli vytvořit seznam S1. To uděláme tak, že projdeme seznam S0, pro každého z členů v tomto seznamu se podíváme na jeho známé a ty přidáme do S1. Pak můžeme obdobným způsobem projít S1 a známé přidat do S2, atd.
Ale má to dva háčky:
- Některý z těchto známých už možná klíč má. Například pokud se znají dva vedoucí A a B, při procházení známých A narazíme na B, ale nechceme ho přidat do S1 (protože už má klíč kvality 0, tak mu nebudeme dávat horší).
- Potřebujeme umět rychle zjistit seznam známých daného člena.
S prvním problémem se vypořádáme tak, že si pro každého člověka poznamenáme, jestli už dostal klíč. K tomu si pořídíme pole D délky N, kde D[i] bude 1, pokud už jsme členovi i dali klíč (zařadili ho do některého seznamu Si), jinak 0.
Takovéto uložení v poli je důležité, protože nám umožňuje rychle (v konstantním čase) testovat, zda už daný člověk má klíč. Kdybychom místo toho měli seznam lidí, kteří dostali klíč, museli bychom pro ověření jednoho člověka celý tento seznam projít, což by trvalo čas O(N).
Ještě zbývá jedna otázka: jak zařídit, abychom uměli rychle zjistit seznam známých nějakého člena? Jednoduše: prostě si budeme pro každého člena seznam známých pamatovat. Tyto seznamy vytvoříme při načítání vstupu: když načteme řádek popisující známost lidí i a j, přidáme j do seznamu známých i a zároveň i do seznamu známých j.
Můžeme si například pořídit seznam Z, jehož prvky budou jednotlivé seznamy známých – Z[i] bude seznam známých i-tého člověka, Z[i][0] bude první známý i-tého člověka, atd.
Na vstup se taky můžeme dívat jako na graf, jehož vrcholy tvoří členové klubu a hrany známosti mezi nimi. Potom výše popsaný seznam Z není nic jiného než reprezentace grafu seznamem sousedů a náš algoritmus je vlastně upravené prohledávání grafu do šířky (liší se tím, že začínáme prohledávat z několika vrcholů současně). Pokud vám ještě tyto pojmy nic neříkají, dočtete se o nich v naší grafové kuchařce.
 30-Z4-3 Uhlazovací válec (Zadání)
30-Z4-3 Uhlazovací válec (Zadání)
Překvapivě, v této úloze nebylo vůbec nic záludného. Pokud znáte libovolný algoritmus na průchod grafu nebo čtvercové mřížky, mohli jste ho s úspěchem použít. Nutným předpokladem pro takto jednoduché řešení je ovšem konstantní velikost desky (v našem případě 3×3), bez něj je úloha výrazně složitější.
Pojďme si připomenout prohledávání do hloubky. Na začátku si na zásobník vložíme levý horní roh, a postupně budeme vytahovat možná umístění válce. Navštívená políčka si musíme někam poznamenat, abychom je nenavštěvovali vícekrát. Tomuto účelu poslouží třeba další mřížka booleovských proměnných. Poté započítáme všechna políčka, která válec na tomto umístění pokrývá – i toto započítání si ale musíme u každého políčka poznamenat, odděleně od navštívení. Na závěr pro každého ještě nenavštíveného souseda zjistíme, zda se na dané místo dá válec posunout, a pokud ano, vložíme jej na vrchol zásobníku.
Pokud bychom chtěli být extra úsporní, stačí nám ověřit nepřítomnost překážek těsně za hranami plochy zabrané válcem. Protože je však v naší úloze válec konstantně velký (a prakticky velmi malý), nemusíme se s tím zatěžovat a můžeme klidně kontrolovat celou plochu čtyřikrát.
Jestliže jste místo explicitního zásobníku (např. v seznamu) využili rekurze a zásobníku volání funkcí, mohli jste narazit na to, že ve vyšších programovacích jazycích je cena za volání funkce příliš vysoká. Pokud to jde tak snadno jako v této úloze, doporučujeme se rekurzi vyhnout, a to zejména v Pythonu.
Takto upravené prohledávání si zachovává svou časovou složitost, která je lineární s počtem políček, která prohledáváme. Znovu připomínáme, že je ve skutečnosti násobena velikostí plochy, která se však díky konstantní velikosti „schová do O-čka“.
 30-Z4-4 Ohrazení zahrádky (Zadání)
30-Z4-4 Ohrazení zahrádky (Zadání)
O kolících na x-ové ose budeme říkat, že jsou vodorovné, kolíkům na y-ové ose budeme říkat svislé. Podle zadání jsme na vstupu dostali seznamy vodorovných a svislých kolíků X a Y délky m a n – konkrétně v seznamu X jsou x-ové souřadnice všech vodorovných kolíků a v seznamu Y jsou y-ové souřadnice všech svislých kolíků.
Aby Zuzka zatlučením posledního kolíku vytvořila obdélníkovou zahradu rovnoběžnou s osami, musí ho zatlouct přesně napravo od nějakého svislého kolíku a zároveň přesně nahoru nad nějaký vodorovný kolík. Jinými slovy, Zuzka může kolík zatlouct jen na pozice tvaru [x, y], kde x je prvek pole X a y je prvek pole Y. V takovém případě bude mít zahrada objem x·y jednotek.
Můžeme tedy vyzkoušet všechny možnosti, jak vybrat nějaké x z pole X a k němu y z pole Y. Pro každou možnost pak můžeme spočítat x ·y, ověřit, zda tento součin nepřekračuje Q, a pokud nepřekračuje, porovnat ho s dosavadním maximem a případně součin prohlásit za nové maximum.
Takový algoritmus bude mít časovou složitost O(mn), protože máme m ·n možností na výběr x a y. Paměťová složitost je O(m+n), protože nám stačí pamatovat si jen X a Y.
Zrychlujeme…
S takto pomalým řešením se ale (samozřejmě) nespokojíme. V první řadě si všimneme, že náš algoritmus pracuje stejně dobře, ať už jsou na vstupu prvky X a Y uvedené v jakémkoliv pořadí. Zkusíme tedy prvky na začátku vzestupně seřadit (za to nic nedáme, oproti O(mn) je čas na řazení zanedbatelný) a uvidíme, zda neumíme seřazení nějak využít.
Jak se náš algoritmus chová na seřazeném vstupu? Nejprve vezme nejmenší x a k němu bere všechna y od nejmenšího, pak pokračuje o něco větším x' atd. Pro konkrétní x jsou nejdřív součiny x ·y příliš malé (už máme lepší maximum), pak jsou chvíli „tak akorát“ (mají potenciál zvýšit dosavadní maximum) a pak jsou zase příliš velké (přesahují Q).
Chtěli bychom umět přeskakovat příliš malé a příliš velké součiny. Je zřejmé, že jakmile pro konkrétní x přeroste x ·y horní mez Q, budou i všechny další součiny příliš velké a můžeme přeskočit až na zpracování dalšího x. S příliš malými součiny ale podobný trik udělat neumíme.
Pomůžeme si úpravou našeho algoritmu – místo abychom pro jedno x procházeli y od nejmenšího, dokud je součin v mezích, půjdeme naopak od největších y, dokud součin meze překračuje. Jakmile totiž narazíme na první součin x ·y nepřekračující Q, můžeme s ním zkusit vylepšit dosavadní maximum a přeskočit na další x – všechny ostatní součiny budou menší, takže s nimi maximum nezlepšíme.
Zdá se, že jsme se dostali do stejné situace, jako předtím – víme, kdy už máme skončit, ale nevíme, kde máme začít. Tentokrát si ale umíme pomoct: pro konkrétní x nebudeme procházet všechna y od největšího, ale začneme tam, kde jsme skončili s minulým x'. Jelikož x se zvětšují, platí, že pokud byl nějaký součin x' ·y příliš velký, bude i součin x·y příliš velký. Přeskakujeme tedy jen ty y, které pro nás již v minulém kole byly příliš velké, a tím spíš pro nás budou příliš velké teď.
Jaké má toto řešení časovou složitost? Na začátku řadíme obě pole, což zvládáme v O(n log n+m log m). V druhé části sice provádíme m cyklů a v každém můžeme projít až Θ(n) různých y, ale není těžké si rozmyslet, že dohromady vyzkoušíme jen Θ(n + m) různých kombinací x a y: mezi každými dvěma kombinacemi se buď x zvýší nebo y sníží a druhá složka zůstane stejná. Dohromady se ale x může zvýšit nejvýše m-krát a y se může snížit jen n-krát, celkově tedy může být jen n + m kombinací. Časová složitost druhé části je tedy O(n + m), celková časová složitost je O(n log n+m log m). Paměťová složitost zůstává O(n + m).
 30-Z4-5 Sběr jablek (Zadání)
30-Z4-5 Sběr jablek (Zadání)
Kolem každého stromu je nějaký interval, ve kterém jsou jablka nejblíže k němu, a všude jinde bude nějaký jiný strom blíž. Takový interval je z každé strany ohraničený středem mezi naším stromem a nejbližším stromem z dané strany (nebo není ohraničený, když tam žádný další strom není). Když si stromy setřídíme, můžeme si jedním průchodem vyrobit takový interval pro každý strom – jako hranici vždy použijeme střed mezi dvěma stromy.
Teď potřebujeme pro každé jablko najít, do kterého spadá intervalu. Jablka si
také můžeme setřídit podle polohy a pak je postupně projít. Budeme je
procházet zároveň s intervaly, do kterých můžou spadat – pro každé jablko si
posuneme „kurzor“ na interval tak, aby do něj spadalo. Pak se podíváme, jaký je
tam strom, a vypíšeme, jak je od jablka daleko. Když budeme mít hranice intervalů
v poli hranice_intervalu (které začíná mezi prvním a druhým intervalem a končí
nekonečnem), tak by to v kódu mohlo vypadat takto:
nh = 0 # Nejbližší hranice
for jablko in jablka:
# Posuneme si hranici tak, aby byla vždy
# za jablkem. Někdy se tento cyklus nemusí
# vůbec vykonat.
while hranice_intervalu[nh] < jablko:
nh += 1
# Strom je na stejné pozici jako jeho interval
vzdalenost = abs(stromy[nh] - jablko)
print(vzdalenost)
Nalezení hranic i průchod jablky bude potřebovat řádově stejně času jako je stromů, respektive jablek. Setřídění polí provedeme nějakým rozumným algoritmem z knihovny (třeba MergeSort nebo QuickSort) a to bude trvat O(N log N) času pro jablka i stromy. Když budeme mít N stromů a M jablek, budeme potřebovat na celý algoritmus O(N log N + M log M) času.
 30-Z4-6 Analýza nadávek (Zadání)
30-Z4-6 Analýza nadávek (Zadání)
Máme najít v textu délky N podřetězec délky K (budeme mu říkat slovo), který se vyskytuje co nejvíckrát zopakovaný bezprostředně za sebou. Navíc máme slíbeno, že K je mnohem menší než N.
Většinou se hodí začít úplně primitivním algoritmem, který je vlastně jenom překladem zadání. Prostě vyzkoušíme všechna možné slova a pro každé z nich spočítáme, kolikrát po sobě se opakuje. Na to stačí porovnat ho s následujícími K znaky, pak s dalšími K znaky a tak dále.
Jak bude takový „dřevorubecký“ algoritmus rychlý? Máme celkem N-K+1 slov, každé z nich můžeme porovnávat s až N dalšími znaky. To dává časovou složitost O((N-K+1) · N) = O(N2).
Nic moc, řeknete si. Ale jde to snadno zrychlit: Pokud se nějaké slovo S zopakovalo t-krát, tak se žádné jiné slovo začínající během prvních t-1 opakování slova S nemůže opakovat víc než t-krát. Nejpozději po t-tém opakování se totiž zarazíme o stejnou neshodu znaků, o jakou jsme se zarazili u slova S.
Když jsme tedy pro slovo na pozici i našli t opakování, nemusíme příště zkoušet slovo na pozici i+1, ale stačí popoběhnout na pozici i+tK-1. Například pro K=4 a text
OKOPOKOPOKOPAKOPAKOPAKOPAKOPA
objevíme 4 výskyty slova OKOP a pak pokračujeme od KOPA. (KOPO,
OPOK ani POKO se nemohou opakovat víckrát než OKOP.)
Tím pádem každý znak textu prozkoumáme nejvýše K-krát, takže složitost algoritmu klesne na O(NK). To je, pokud zanedbáme závislost na K, jistě nejlepší možné.
Lineární řešení
Také vám vrtá hlavou, jestli existuje algoritmus, který by byl rychlý i pro velké K? Tak tady je.
O znaku na i-té pozici řekneme, že je nadějný, pokud je stejný jako znak na (i-K)-té pozici. Všimneme si, že pokud se nějaké slovo vyskytne dvakrát za sebou, všechny znaky jeho druhého výskytu jsou nadějné. A naopak: pokud najdeme K po sobě jdoucích nadějných znaků, znamená to, že se nějaké slovo vyskytlo podruhé. Platí to i obecněji: slovo se vyskytne t-krát za sebou pravě tehdy, když je v textu (t-1)K po sobě jdoucích nadějných znaků.
Hezky je to vidět na následujícím příkladu (N=22, K=4, nadějné znaky jsou označené hvězdičkami):
ABCDABCEDBCEDBCEDBXYDB
....***..*********..**
Existuje úsek 9 po sobě jdoucích nadějných znaků, takže se nějaké
slovo (BCED nebo CEDB) vyskytuje ⌊9/4⌋+ 1 = 3
krát za sebou.
Našemu algoritmu tedy stačí najít nejdelší úsek po sobě jdoucích nadějných znaků. To jistě zvládne v čase O(N) nezávisle na K.