Čtvrtá série začátečnické kategorie třicátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 25. června 2018 v 8:00, praktické úlohy lze za třetinu bodů odevzdávat až do 2. července 2018
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 30-Z4-1: Statistika sprintů
- 30-Z4-2: Klíče od tělocvičny
- 30-Z4-3: Uhlazovací válec
- 30-Z4-4: Ohrazení zahrádky
- 30-Z4-5: Sběr jablek
- 30-Z4-6: Analýza nadávek
30-Z4-1 Statistika sprintů (8 bodů)
V Kevinově škole probíhá i letos konec školního roku v líné, uvolněné náladě: žáci se už moc nechtějí učit a ani učitelé nechtějí začínat nějakou složitou látku. Dneska mají místo učení úplně jiný program. Na venkovním školním hřišti probíhají tělocvičné testy. Každý žák musí projít několika disciplínami, aby zjistil, jak je fyzicky zdatný v porovnání s ostatními. Jednou z těchto disciplín je i sprint na 100 metrů.
U běžecké dráhy sedí zapisovatel. Dostal za úkol si poznamenávat naměřené časy a určit K nejrychlejších žáků. Bohužel zapisovatel úkol špatně pochopil a místo toho hledá K-tici žáků, kteří běží těsně po sobě a kteří mají v průměru nejmenší čas.
Vstup programu se skládá ze dvou řádků. Na prvním řádku je celkový počet žáků N a číslo K, které vždy bude menší nebo rovno N. Na druhém řádku pak obdržíte N přirozených čísel, což jsou časy běhu žáků v sekundách. Najděte za sebou jdoucí K-tici žáků, která měla nejnižší průměr časů, a vypište index prvního žáka této K-tice. Číslujeme od nuly, takže například pokud nejlepší průměr měli první, druhý až K-tý žák v pořadí, na výstupu musí být nula.
8 4 28 34 23 10 10 16 10 25
3
30-Z4-2 Klíče od tělocvičny (10 bodů)
Kevin netušil, že zapisovatel času sprintů je zmatený, a zaběhl svých 100 metrů na průměrný čas. Proto ho velmi překvapilo, když se za ním na konci dne zastavil učitel tělocviku. „To jsem netušil, že jsi takový talent! Musíš co nejdříve přijít do našeho běžeckého klubu.“ Než se Kevin stačil nadechnout, tak mu vrazil do ruky klíče od budovy klubu a řekl mu, kdy a v kolik hodin má přijít.
Když ale Kevin přišel na místo, zjistil, že se nemůže dostat dovnitř. Členové klubu si klíče mezi sebou kopírovali tak dlouho, že se klíče staly nekvalitními a přestaly odemykat. Kevin má za úkol zjistit, jak rozdat nové klíče, aby se tohle nestalo.
Máte k dispozici seznam členů klubu a víte, kteří členové se mezi sebou osobně znají. Někteří z členů fungují jako vedoucí klubu a ti dostanou originál nového klíče, jehož kvalitu označujeme nulou. Vedoucí všem lidem, které znají, tento klíč nakopírují, ovšem kopie už bude mít horší kvalitu 1. A takhle to pokračuje dál: když nějaký člen klubu dostane klíč s kvalitou X, nakopíruje ho svým kamarádům, kteří ještě žádný nemají, a tato kopie bude mít kvalitu X+1.
Kevin zjistil, že klíč nefunguje, pokud jeho kvalita překročí nějaké číslo K. Zjistěte, kolik členů klubu dostane klíč, který dokáže odemknout dveře.
Na prvním řádku vstupu si přečtete počet členů klubu N, počet M dvojic, které se znají, počet vedoucích V a konečně číslo K. Druhý řádek obsahuje V čísel, která označují vedoucí klubu (číslujeme od nuly, takže každý člen má číslo od nuly do N-1). Pak následuje M řádků, na každém je dvojice čísel členů, kteří se spolu znají.
Na výstup vypíšete jediné číslo – počet členů klubu, kteří budou mít funkční klíč (s kvalitou menší nebo rovnou K).
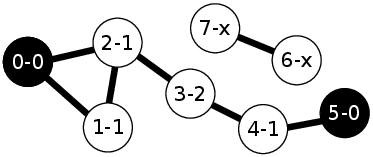
Vstup a výstup odpovídá obrázku. První číslo je pořadové číslo člena, druhé číslo
je kvalita jeho klíče (x znamená, že klíč nedostane). Černou barvou jsou
značeni vedoucí.
8 7 2 1 0 5 0 1 0 2 1 2 2 3 3 4 4 5 6 7
5
30-Z4-3 Uhlazovací válec (10 bodů)
Když v klubu začala hodina běhu, tělocvikář začal dávat Kevinovi pěkně do těla. Třebaže se mu Kevin snažil vysvětlit, že až tak velký talent na sprint zase není, učitel mu to nevěřil a myslel si, že je jen líný. Prý aby Kevin zesílil, dal mu za úkol vzít těžký ruční válec a uhladit plochu velkého fotbalového hřiště.
Hřiště si můžeme představit jako čtvercovou mřížku. Pole v mřížce mohou být buď průchozí (to odpovídá povrchu hřiště), nebo neprůchozí (to mohou být tyče, branky nebo lavičky). Ruční válec má rozměry 3×3 políčka a vždy se musí nacházet jen na průchozích polích. Kevin má za úkol tahat válec po hřišti, aby uhladil co nejvíce průchozích polí. Je ale možné, že kvůli překážkám se do všech míst hřiště nedostane.
Váš program dostane na vstup výšku a šířku hřiště a následně takový
popis, že X znamená obsazené pole, O znamená volné pole. Válec se
na začátku nachází v levém horním rohu (máte jistotu, že tato pole budou
neobsazená). Vypište maximální počet průchozích polí, která Kevin dokáže
zarovnat. To, že skutečný válec by potřeboval nějaký prostor na otočení,
zanedbejte – v této úloze se chová spíše jako velká deska, kterou můžeme
posouvat na jakoukoliv stranu.
6 5 OOOXO OOOXO OOOXO OOOOO OOOOO OOOOX
21
30-Z4-4 Ohrazení zahrádky (12 bodů)
Kevin uhladil i poslední část hřiště a vyčerpaně si sedl na válec. Všiml si, že hned za plotem u hřiště začíná městská zahrádkářská kolonie. Byl hezký den a na záhonech pracovala spousta lidí. Vtom si Kevin všiml, že na něj někdo mává. Byla to Zuzka, kamarádka ze školy. Stála na travnaté ploše vedle záhonů, protože si chtěla vyměřit prostor pro svoji vlastní zahrádku. Nevěděla si ale rady s tím, jak by vlastně měla být velká.
Zahrádkářská kolonie se nachází na rovině se souřadnicovými osami. Zuzka do roviny zatloukla několik kolíků – jeden do pozice [0, 0], několik dalších do pozic [X1, 0], [X2, 0] až [Xm, 0] a několik do pozic [0, Y1], [0, Y2] až [0, Yn]. Všechna Xi i Yi jsou kladná celá čísla, kolíky se tudíž nacházejí na kladných poloosách.
Zuzka má ještě jeden kolík a přemýšlí, kam ho zatlouct, aby spolu s dalšími třemi kolíky vytvořila obdélníkovou zahradu, která bude rovnoběžná s osami. Na jednu stranu chce, aby obsah obdélníku byl co největší, na druhou stranu ale obsah nesmí překročit číslo Q, aby se vyhnula velkým platbám za pronájem.
Napište Zuzce program, který na prvním řádku vstupu dostane počet bodů Xi, počet bodů Yi a číslo Q, na dalším řádku všechny souřadnice Xi a na třetím řádku všechny souřadnice Yi. Program vypíše obsah největší možné zahrádky, který nepřesahuje Q.
Ukázkový vstup a výstup odpovídají obrázku. Šedou barvou je zvýrazněné jedno z řešení.
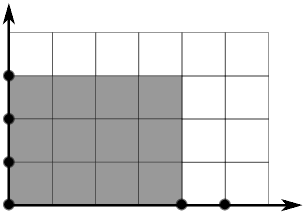
2 3 14 5 4 1 3 2
12
Poznámka: Pokud používáte programovací jazyk, ve kterém mají čísla omezený
rozsah (jako například C nebo Java), vězte, že pro uložení výsledku je potřeba
64bitový celočíselný typ (long long v C, long v Javě).
30-Z4-5 Sběr jablek (12 bodů)
Kevin se běhání věnoval dál, ale také začal Zuzce pomáhat na zahrádce. Na konci léta pomáhal se sběrem jablek v sadu, který byl součástí zahrádkářské kolonie. Protože ale při sázení jabloní nezbývalo mnoho místa, jsou všechny stromy umístěné na jedné přímce. Kevin před nějakou dobou četl knížku o statistice a zajímalo by ho, jak daleko typicky padají jablka od stromů.
Máte k dispozici popis přímky představující sad. Na přímce jsou dva druhy bodů: stromy a jablka. Předpokládáme, že každé jablko spadlo ze stromu, který je k němu nejblíže. Pro každé jablko vypočtěte vzdálenost k nejbližšímu stromu, aby mohl Kevin vytvořit statistiku.
Příklad: Pro stromy na pozicích 4, 1 a 6.7 a jablka na pozicích 2, -2, 4, 6 jsou vzdálenosti jablek k nejbližším stromům postupně 1, 3, 0 a 0.7.
30-Z4-6 Analýza nadávek (14 bodů)
Už jsme zjistili, že zahrádkářská kolonie a sportovní klub spolu sousedí. Mezi nimi se ale právě rozhořel spor o neobsazený pozemek blízko hřiště. Sportovní klub by tu chtěl postavit nové šatny, kdežto zahrádkáři nový dřevník pro uchovávání nástrojů. Hlavní vedoucí obou skupin se sešli na městské radnici. K žádné dohodě ale nedošlo, místo toho se pořádně pohádali!
Kevin na schůzi nebyl, ale dostal se mu do ruky strojový přepis všeho, co na schůzi zaznělo. Tady máte příklad jedné části přepisu:
NEHLUPAKUHLUPAKUCHCEMESATNYPITOMCINEPATRITONAM
Spousta nadávek se v textu bezprostředně za sebou opakuje. Kevin chce v přepisu
najít podřetězec délky přesně K, který se v něm co nejvíckrát bezprostředně za sebou
opakuje. Například pro K = 7 to je podřetězec HLUPAKU (vyskytuje se
dvakrát za sebou).
Můžete předpokládat, že K je rozumně malé, nemusíte optimalizovat složitost na jeho hodnotu.