První série začátečnické kategorie třicátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 4. prosince 2017 v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 30-Z1-1: Kevinova nepatnáctka
- 30-Z1-2: Sářiny loutky
- 30-Z1-3: Petrovo luštění zprávy
- 30-Z1-4: Zuzčin projekt
- 30-Z1-5: Třicet totemů
- 30-Z1-6: Zuzčina první šifra
30-Z1-1 Kevinova nepatnáctka (8 bodů)
Kevin jel na výlet na druhou stranu republiky a už strávil ve vlaku více než sedm hodin – už ho nebavilo dívat se z okna na stále se pohybující krajinu. Všiml si, že spolucestující na opačné straně kupé si hrál s hlavolamem Patnáctkou.
Jedná se o krabičku, do které se vejde 4 × 4 čtverečků, ale jeden chybí. Každý čtvereček má nějaké číslo. Kevin však byl tak znuděný, že jej nezajímala ani čísla na čtverečcích, ani jak se hlavolam řeší.
Místo toho pozoroval, jak se při řešení hlavolamu pohybuje díra. Začal si rozmýšlet různé posuny v hlavolamu a předpovídal, kde díra skončí. V případě, že posun nelze uskutečnit, přeskočí se. Po krátké chvilce si řekl, že krabička je zbytečně malá, a tak začal přemýšlet i o větších krabičkách.
Dokážete i vy předpovědět, kde po provedení Kevinových pohybů skončí díra?
Tvar vstupu a výstupu: Na prvním řádku dostanete čísla M a N – počet
řádků a sloupců v krabičce. Následující řádek obsahuje
dvojici čísel, která reprezentuje číslo řádku a sloupce, ve kterém se nachází
díra. Na třetím řádku dostanete počet posunů. Poslední řádek má zaznamenané
jednotlivé posuny jako znaky <, >, ^, v.
Na výstupu očekáváme čísla výsledného řádku a sloupce, ve kterém díra skončí. Nejvrchnější řádek a nejlevější sloupec jsou očíslované jedničkou.
4 4 2 4 10 <<<v>>^^^^
1 3
30-Z1-2 Sářiny loutky (10 bodů)
Sára se začala věnovat novému koníčku – sběru dřevěných loutek. Také jich už dost nasbírala. Nelíbí se jí však, že má všechny loutky pohozené ve skříni. Chce si proto koupit loutkové věšáky, na které si své loutky pěkně vystaví.
Na každý věšák se vejdou nejvýše dvě loutky. Bohužel dnešní věšáky jsou vyráběny nekvalitně, a ještě k tomu jsou dřevěné loutky docela těžké. Sára zjistila, jakou největší váhu věšáky snesou.
Sáře rovněž už nezbylo moc kapesného, proto by nechtěla kupovat zbytečně hodně věšáků. Pomozte Sáře zjistit, kolik nejméně věšáků si musí koupit, aby mohla rozmístit loutky podle svých představ.
Tvar vstupu: Na prvním řádku se nacházejí čísla N, počet loutek, a K říkající nejvyšší váhu unesitelnou věšákem. Následuje N řádků, na kterých jsou váhy jednotlivých loutek.
Tvar výstupu: Od vás očekáváme jedno číslo – nejmenší počet věšáků, na které Sára už bude moct své loutky rozmístit.
4 20 20 8 15 10
3
30-Z1-3 Petrovo luštění zprávy (10 bodů)
Petr si užíval dovolenou u moře a rozhodl se poslat Kevinovi zprávu, jak se mu tam líbí. Kevin mu hned odpověděl.
V té době byl však Kevin na výletě v horách. A jak to na horách bývá, měl hodně slabý signál a odpověď se po cestě poškodila. Některá písmena ve zprávě byla pozměněna.
Když Petrovi přišla poškozená Kevinova odpověď, hned Kevina požádal, aby mu odpověď poslal ještě vícekrát.
Jakmile mu přišly kopie, každá jinak poškozená, začal luštit zprávu – pro danou pozici vybral písmeno, které se v každé zprávě vyskytlo nejčastěji. Jak si dokážete představit, tento proces je velmi zdlouhavý. Pomozte Petrovi s luštěním!
Tvar vstupu: Na prvním řádku najdete počet zpráv N a jejich délku. Následuje N řádků, kde na každém je přijatá poškozená zpráva. Zprávy budou používat pouze velká písmena anglické abecedy.
Tvar výstupu: Na výstup vypište vyluštěnou zprávu. Jestliže takových zpráv najdete více, vyberte libovolnou z nich.
4 22 JSIMVBEIKYDMCHPRSITMDY JSEMVBESKDDEVHPRSITADF JSEMVBESWYDECHPRSITATY KSEUIBFSKYRECRPRSITADY
JSEMVBESKYDECHPRSITADY
30-Z1-4 Zuzčin projekt (12 bodů)
Zuzka našla na nástěnce zajímavý letáček. V něm byla pozvánka k účasti do velkého prázdninového projektu, do kterého by se mohla zapojit celá škola.
Tento projekt byl velmi rozsáhlý, tudíž se všichni domluvili na systému vedení tohoto projektu. Jelikož se nejlépe pracuje se svými kamarády, každý účastník může oslovit své kamarády, aby byli jeho podřízenými. Rovněž si každý uvědomil, že je pro něj samozřejmě nejvýhodnější přijmout nabídku, která je „nejblíže“ k vedoucímu projektu.
Přišly však nemalé spory o to, kdo projekt vlastně bude vést. Někteří účastníci rovněž chtěli vědět, kolik vlastně budou mít pomocníků, než se na projektu skutečně začne pracovat. Dokážete Zuzce pomoci odpovědět na otázku, kolik přímých podřízených bude tázající mít při volbě daného vedoucího projektu?
Tvar vstupu: Na prvním řádku najdete dvojici čísel N a D. Účastníci projektu jsou očíslovaní 0 … (N-1). Následuje N řádků, kde na i-tém řádku jsou zaznamenaní kamarádi i-tého účastníka, seřazení od nejmenšího čísla. Dále následuje D řádků s dotazy jako dvojice čísel udávající vedoucího projektu a dotazovaného účastníka.
V případě, že dostane účastník více nabídek ve stejné „vzdálenosti“ od vedoucího, vybere si tu od kamaráda s nižším číslem. Pokud by účastník žádnou nabídku nedostal, tak je počet jeho podřízených nulový.
Tvar výstupu: Na výstup vypište na každý řádek číslo udávající počet přímých podřízených dotazujícího.
6 3 1 2 5 0 2 3 0 1 3 4 1 2 4 2 3 0 5 0 0 1 0 0
2 1 3
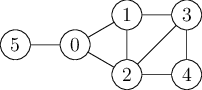
Výše jsme pro ukázkový vstup vyobrazili všechny známé kamarádské vztahy a níže naleznete pro každý ze tří dotazů znázorněno, jak vypadá situace (vedoucí je vždy nahoře a zvýrazněné vrcholy jsou ty, na jejichž počet přímých podřízených se ptáme).
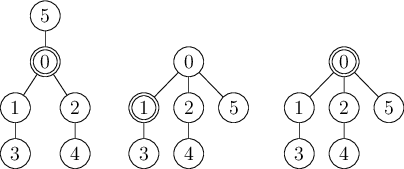
30-Z1-5 Třicet totemů (12 bodů)
Kevin a Petr spolu s dalšími 28 dětmi jeli společně na letní tábor. Užívali si hry i přednášky a ten den nastal čas na stavění totemů, kdy si každý účastník mohl postavit vlastní.
Jako základní suroviny ke stavění totemů byly venku vystavěné hromady z různě vysokých klád. Každému byla přidělená jedna hromada klád, přičemž nebylo povoleno využívat klády ostatních pro férové podmínky.
Kevin se spolu s Petrem domluvili, že postaví stejně vysoké totemy. S takovými kládami se těžce manipuluje a oba nemají žádné nářadí, kterým by je mohli rozříznout na menší. Proto Kevin chce odebrat a použít z vršku své hromady prvních K klád a Petr prvních P klád ze své hromady tak, aby se výsledný součet výšek použitých klád rovnal.
Vymyslete způsob, jak pro zadané délky klád na obou hromadách najít všechny kombinace K a P, které mohou Kevin s Petrem použít (zjistěte kombinace, kolik klád každý musí ze svého vršku hromady sundat a použít), aby se výšky obou totemů, tedy součty výšek použitých klád, rovnaly.
5 7 3 9 6 8 9 7 2 4 5
4 3 5 5
Vršky hromádek jsou nalevo, výsledné výšky totemů jsou 24 nebo 30. Tato ukázka je jen orientační – jde o teoretickou úlohu.
30-Z1-6 Zuzčina první šifra (14 bodů)
Zatímco Kevin se vracel z letního tábora, Zuzka připravovala pro Kevina malou šifru jako zábavu.
Po zahradě začala rozmísťovat písmena tvořící zprávu, kterou má Kevin za úkol rozluštit. Aby Kevin znal pořadí písmen, při položení každého písmene zapsala Zuzka na papír souřadnice, definované jako počet centimetrů na sever a na východ od posledního položeného písmenka.
Při pokládání ale nekontrolovala, zda na daném místě už nějaké písmenko je. Na některých pozicích může být tudíž více písmenek. Zuzka by ráda věděla, kolik a na jakých souřadnicích je jich položeno nejvíce.
Vaším úkolem je najít co nejefektivnější způsob, jak tuto informaci může Zuzka zjistit ze svých zápisků. Můžete předpokládat, že zahrada je nekonečně rozlehlá rovina a první písmenko má v zápiscích napsaný rozdíl od souřadnic (0,0).