Druhá série začátečnické kategorie třicátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 5. února 2018 v 8:00, praktické úlohy lze za třetinu bodů odevzdávat až do 12. února 2018
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Zadání úloh

• 30-Z2-1: K-k-koktavý K-K-Kevin
• 30-Z2-2: Hřiště pro tarantule
• 30-Z2-3: Klonování pavouků
• 30-Z2-4: Příliš bílý displej
• 30-Z2-5: Spokojenost s výstavou
• 30-Z2-6: Skořápky

30-Z2-1 K-k-koktavý K-K-Kevin (8 bodů)

„P-p-p-pomoc!“ vrazil Kevin ráno do třídy. „Proč jdeš pozdě?“ ptala se přísně učitelka. Od začátku hodiny uplynulo už deset minut. „P-p-před-de d-d-dveřmi…“ snažil se odpovědět Kevin, ale bylo na něm vidět, že je celý rozčílený.

Aby byla učitelka schopná pochopit, co se Kevinovi stalo, musí si poradit s jeho dočasnou koktavostí. Chtěla by z jeho vět odstranit všechna přebytečná písmena, která Kevin vykoktává víckrát po sobě. Pomůžete jí?

Na vstupu váš program obdrží záznam Kevinovy řeči. Na výstupu chceme pro každý řádek tu samou řeč, ale stejné znaky vedle sebe budou vypsány jenom jednou. Platí to i pro mezery, naopak s ch si lámat hlavu nemusíte (skládá se ze dvou znaků).

Ppppommmoccc
vvvvyyysssstrasssil
  mmmne    vvvelky
pppavvouk

Ppomoc
vystrasil
 mne velky
pavouk

Řešení

30-Z2-2 Hřiště pro tarantule (10 bodů)

Tak už to bylo jasné: Kevin, který se bojí pavouků, na školní chodbě na jednoho narazil, konkrétně na docela vypasenou tarantuli! Přinesl je do školy učitel biologie spolu s dřevěnou deskou, „hřištěm“, na které je cvičí.

Tarantulí hřiště je vlastně mřížka s K×K poli. Na hřiště umístíme K očíslovaných tarantulí tak, aby na začátku stály na diagonále, první tarantule vlevo nahoře a další vždy o řádek níže a sloupec napravo. Cvičení je rozděleno na několik kroků, kde v každém kroku dostane každá tarantule instrukci, jak se pohnout – doleva, doprava, nahoru, dolů, nebo zůstat stát na místě. Všechny své instrukce provedou najednou.

Pokud by měl pavouk přepadnout přes okraj, tak svůj krok neprovede. Nesmí se však stát, že v nějakém kroku stojí dva nebo více pavouků na jednom poli, v takovém případě hejno zpanikaří a rozuteče se. (Nevadí, pokud dvě tarantule stojí vedle sebe a v nějakém kroku si prohodí místa, ale na konci kroku musí mít každá svoje pole jenom pro sebe.)

Na prvním řádku máte zadané K a počet kroků N. Na každém z následujících N řádků je popis jednoho kroku. Jeden krok je popsaný pomocí K znaků <, >, ^, v a o (zůstaň stát), kde i-tý znak představuje instrukci pro i-tého pavouka. Vypište na výstup číslo prvního kroku, po jehož provedení se dvě nebo víc tarantulí srazí na nějakém poli, nebo -1, pokud k tomu nikdy nedojde (číslujeme od jedničky).

3 4
>o^
v^o
o><
<<o

3

Řešení

30-Z2-3 Klonování pavouků (10 bodů)

Jakmile se všechny tarantule našly a byly bezpečně uloženy v teráriu, vysvětlil učitel Kevinovi, že kdysi pracoval ve výzkumném ústavu, kde se pokoušeli klonovat pavouky. V každém experimentu začali s jedním jediným pavoukem, kterému odebrali DNA a vytvořili buď jednoho, dva, nebo také žádného „potomka“. Vzniklí pavouci (pokud nějací byli) se poté stejným způsobem klonovali dál a takhle vzniklo mnoho generací pavouků. Nikdy se však z jednoho pavouka nepodařilo naklonovat více než dva nové jedince.

Tvar vstupu: Na jediném řádku je popsán rodokmen původního pavouka (který obsahuje informace o všech jeho potomcích). Popis rodokmenu jednoho pavouka je zapsán ve tvaru (AnB), kde n je jméno pavouka a A a B jsou rodokmeny jeho potomků (popsané stejným způsobem).

Pokud pavouk má méně než dva potomky, můžeme místo A nebo B napsat znak _ znamenající „tady žádný potomek není“. Pavouka bez potomků bychom tedy popsali jako (_n_), ale jako zkratku můžeme místo toho psát jen n.

Jména pavouků se skládají z jednoho malého písmene anglické abecedy a nemusí být unikátní.

Uvažte následující rodokmen:

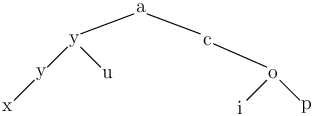
Ten lze zapsat např. jako (((xy_)yu)a(_c(iop))) nebo třeba (((xy_)yu)a(_c((_i_)op)).

Tvar výstupu: Pro každého pavouka, který nemá potomky, vypište na zvláštní řádek jeho rod: jména jeho předchůdců (počínaje tím, který už žádného předchůdce nemá) a jméno pavouka samotného. Rod libovolného levého potomka vždy vypisujte dřív než rod příslušného pravého potomka.

(((xy_)yu)a(_c(iop)))

ayyx
ayu
acoi
acop

Řešení

30-Z2-4 Příliš bílý displej (12 bodů)

Zpráva o uprchlých tarantulích se rychle dostala k řediteli školy. Ten si uvědomil, že pokud by učitel biologie vzal do školy víc zvířat, která chová doma, mohla by se z toho udělat na chodbách školy poučná výstava. Kevin měl na začátek výstavy zapojit počítač, kde si návštěvníci budou moci najít další informace. Ve skladech školy ale Kevin našel jen starý černobílý panel, který navíc přestával fungovat, pokud na něm svítilo příliš mnoho bílých bodů.

Předpokládejte, že displej má S ×R bodů. Na začátku jsou všechny body zhasnuté (černé). Dostanete více požadavků na rozsvícení nějaké obdélníkové oblasti na displeji. Rádi bychom věděli, kolik bodů bude po provedení všech požadavků rozsvícených.

Tvar vstupu: Na prvním řádku jsou čísla S, R a K, kde S je počet bodů na šířku, R na výšku a K počet požadavků. Následuje K řádků s požadavky: na každém jsou čtyři čísla X₁, Y₁, X₂ a Y₂, která představují požadavek „rozsviť body obdélníku, jehož horní levý roh je na souřadnicích [X₁,Y₁] a spodní pravý roh na souřadnicích [X₂,Y₂]“.

První souřadnicí je vždy číslo sloupce a druhou číslo řádku, číslujeme od jedničky a levého horního rohu displeje. Může se stát, že přijde požadavek na rozsvícení bodů, které už rozsvícené jsou, pak je necháte být.

Tvar výstupu: Vypište počet rozsvícených bodů.

3 5 2
2 2 3 4
1 3 2 4

8

Řešení

30-Z2-5 Spokojenost s výstavou (12 bodů)

Kevin se Zuzkou se jednou domluvili, že na výstavu zajdou spolu. Aby si mohli snadno porovnat dojmy, dá Kevin i Zuzka každému zvířeti číselné hodnocení. To může být kladné, pokud se jim zvíře líbí, nebo záporné, pokud nelíbí (u Kevina samozřejmě pavouci). Výstava je umístěna v jedné dlouhé školní chodbě, takže po prohlédnutí si Kevin i Zuzka zvlášť zapsali nějakou posloupnost celých čísel.

Při porovnávání výsledků Kevina napadlo, že by z nich mohl zjistit, jakou průběžnou spokojenost měl každý z nich během procházení výstavy. Průběžná spokojenost po zhlédnutí i-tého zvířete se spočítá jako součet všech hodnocení od prvního zvířete do i-tého. Stalo se někdy během prohlížení, že by on i Zuzka měli stejnou spokojenost? Přitom není nutné, aby v té chvíli oba byli u stejného zvířete.

Tvar vstupu: Na prvním řádku dostanete počet zvířat na výstavě N. Na druhém řádku je posloupnost N celých čísel, která představují Kevinovo hodnocení, na třetím řádku N čísel se Zuzčiným hodnocením. Číslujeme od jedničky.

Tvar výstupu: Pokud je možné najít v Kevinově posloupnosti podposloupnost od 1 do K a v Zuzčině posloupnosti podposloupnost od 1 do L takové, že součty těchto podposloupností se rovnají, vypište na jeden řádek K a L. Jinak bude výstupem programu řetězec NEEXISTUJE.

5
-3 6 1 -5 3
5 -1 -1 2 4

2 3

Pokud by vám zadání něco připomínalo – jde o to samé, jako v úloze s totemy v minulé sérii, tentokrát však máme povolená záporná čísla.

Řešení

30-Z2-6 Skořápky (14 bodů)

Poslední den výstavy učitel žákům nabídl, aby si s ním zahráli skořápky, a vítěz že dostane zvláštní cenu.

Jak se hrají skořápky? Vedoucí hry (skořápkář) má k dispozici N neprůhledných kelímků a kuličku. Jedno kolo probíhá tak, že kelímky srovná vedle sebe, aby byly dnem vzhůru, a kuličku schová do jednoho kelímku. Pak začne kelímky v řadě rychle prohazovat mezi sebou a poté, co skončí, musí ostatní hráči hádat, v jakém kelímku se kulička nachází.

Učitel byl v roli skořápkáře hbitý, ale Kevin byl bystrý a dařilo se mu. O jedné pauze mu však zvědavost nedala a nahlédl do učebny biologie, aby zjistil, o jakou cenu se vlastně hraje. Hned vzápětí zděšeně uskočil – nápis cena pro vítěze byl na terárku s tarantulí!

Tak tohle si Kevin domů v žádném případě nevezme. Jeden z jeho spolužáků si během hraní skořápek zaznamenával do notebooku pohyby kelímků, aby bylo jisté, že učitel nepodvádí. Kevin k němu nenápadně přišel a připsal jeden tah do záznamu z posledního kola, kdy vyhrál. Doufá, že při kontrole bude tohle kolo prohlášené za neplatné a on skončí s méně body.

Jak vypadá záznam jedné hry? Pamatujeme si, že máme N kelímků, dále pak pozici kuličky na začátku a konci hry. Také si pro každý učitelův tah pamatujeme X a Y, což jsou čísla kelímků, které v tomto tahu prohodil mezi sebou. Ve všech případech čísla označují, o kolikátý kelímek zleva se jedná (tj. kelímky nemají stabilní přiřazení čísel).

Máme záznam jedné hry, o kterém víme, že byl původně korektní (pokud bychom hru odsimulovali, tak kulička skutečně skončí v té pozici, jak bylo zadáno). Arachnofob Kevin tam však vložil jeden tah navíc, kvůli kterému teď záznam nesedí. Dokážete zjistit, o který tah šlo? Je-li více možností, vypište libovolnou z nich.

Řešení