První série dvacátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 26-1-1: Blokující signály
- 26-1-2: Přeskládání nákladu
- 26-1-3: Plynové kapsy
- 26-1-4: Oprava databáze
- 26-1-5: Senzory
- 26-1-6: Hydroponie
- 26-1-7: Mravenci
- 26-1-8: Turingova strojovna
26-1-1 Blokující signály (Zadání)
Řekněme, že dokážeme zastavit nějaký signál v uzlu X. Co to znamená? To znamená, že můžeme z hlavního počítače poslat blokující signál, který do uzlu X dorazí ve stejný moment jako ten vadný.
Všimněme si, že když můžeme poslat z hlavního počítače signál, který dorazí do uzlu X v čase T, tak můžeme poslat i signál, který dojde kdykoliv potom. Můžeme totiž signál z hlavního počítače jednoduše vyslat později.
Ke každému uzlu X tedy existuje nějaký minimální čas T0 takový, že dokážeme zablokovat každý vadný signál, který do uzlu X dorazí nejdříve v čase T0. Speciálně pro hlavní počítač je T0 rovno nule: pokud vadný signál prochází hlavním počítačem, stačí si na něj počkat.
Na každý uzel X, který je nějak spojený s hlavním počítačem, můžeme nejdříve dosáhnout v čase, za který stihneme přejít nejkratší cestou z hlavního počítače do uzlu X. Stačí si tedy zjistit délku nejkratších cest z počátku do všech ostatních uzlů, čímž získáme všechny časy T0.
Tahle úloha je (jak si jistě zkušenější řešitelé všimli na první pohled) grafová. Na zjištění délek všech nejkratších cest z nějakého daného vrcholu se v obecném grafu dá použít třeba Dijkstrův algoritmus, který jde naprogramovat tak, aby seběhl v čase O(M + N log N) na grafu s N vrcholy a M hranami. Protože ale v této síti jsou všechny hrany (neboli spojení mezi počítači) stejně dlouhé, můžeme nejkratší cesty najít prostým prohledáváním do šířky, což se stihne za O(M + N). Prohledávání do šířky si můžete představit jako postupné „oloupávání“ sítě: nejdříve utrhneme hlavní počítač, pak všechny počítače na něj napojené (tedy ve vzdálenosti 1), pak všechny napojené na ně (2 kroky daleko), a tak dále. Na detaily implementace se můžete podívat ve zdrojáku vzorového řešení.
26-1-2 Přeskládání nákladu (Zadání)
Problém rozdělení kontejnerů do skladišť můžeme převést na obarvování neorientovaného grafu. Kontejnery budou vrcholy, doporučení budou hrany mezi nimi a obarvení vrcholů dvěma barvami bude znázorňovat jejich rozdělení do skladišť.
Naším cílem je obarvit vrcholy grafu tak, aby hran vedoucích mezi vrcholy stejné barvy (tedy nesplněných doporučení) byla nejvýše polovina.
Ve speciálním případě, kdy bychom měli slíbeno, že graf je čistě bipartitní (tedy že se dá rozdělit na dvě množiny, kde hrany vedou jen mezi množinami a ne uvnitř), bude obarvení vrcholů dvěma barvami triviální.
Dokud budeme mít nějaký neobarvený vrchol, budeme opakovat toto: obarvíme ho první barvou, všechny jeho sousedy druhou, všechny sousedy sousedů opět první a tak dále. Protože každý vrchol sousedí pouze s vrcholy z opačné partity, povedlo by se nám takto splnit všechna doporučení u každého z vrcholů.
Pro bipartitní grafy je to tedy snadné. Jak to ale bude v obecném případě? Už se nám asi nepovede splnit všechna doporučení, ale můžeme se pokusit splnit jich alespoň polovinu. (Pokud bychom jich však chtěli splnit co nejvíc, už by šlo o NP-úplnou úlohu.)
Náš algoritmus bude pracovat po krocích a v každém kroku se bude lokálně pokoušet splnit alespoň polovinu doporučení. Nejdříve se podíváme, jak bude vypadat jeden jeho krok, a potom si dokážeme, že tím splníme alespoň polovinu doporučení i globálně.
Krok algoritmu:
- Vezmi libovolný neobarvený kontejner.
- Spočítej, kolik má sousedů které barvy.
- Pokud má sousedů jedné barvy méně, obarvi ho touto barvou. Jinak libovolně.
- Dokud nejsou všechny kontejnery obarveny, pokračuj bodem 1.
Pro účely dokazování přiřadíme každé doporučení jen jednomu z dvojice kontejnerů – tomu obarvenému později (tím si určitě nic nepokazíme, neboť jednotlivá doporučení ani jejich počet se nijak nezmění).
Každý z kontejnerů bude tedy mít svou vlastní množinu doporučení. Ale to jsou přesně ta doporučení, která jsme uvažovali v bodu 2 algoritmu a obarvením kontejneru jsme jich splnili alespoň polovinu. U každého kontejneru je tedy alespoň polovina doporučení splněna, takže v součtu přes všechny kontejnery musí být splněna také alespoň polovina doporučení. A tím je splněno i zadání.
Zbývá ještě časová a prostorová složitost. Vše, co si musíme pamatovat, je nějaký seznam vrcholů a ke každému vrcholu seznam jeho hran, takže paměťová složitost je O(N+M).
Časová složitost je mírně složitější. Provedeme sice N kroků algoritmu a v každém se můžeme podívat až na M hran (což by mohlo vést na O(MN)), ale stačí si uvědomit, že celkově se za celý běh programu podíváme maximálně na 2M konců hran a tedy výsledná časová složitost bude jen O(N+M).
26-1-3 Plynové kapsy (Zadání)
Jednoduché řešení
Pro každý dotaz prostě projdeme příslušný interval zleva doprava a pokud se aktuální znak bude shodovat s předchozím, přičteme jedničku. Toto řešení je ale pomalé.Rychlé řešení
Připravíme si pomocné pole. Na pozici i budeme mít uložený počet bezpečných míst v intervalu <0, i>. Tomu se říká prefixový součet. Potom při dotazu na <i, j> stačí od j-té pozice odečíst (i-1)-tou. Tím od všech bezpečných pozic nalevo od pravého konce intervalu odečteme ty nalevo od levého konce intervalu, tedy zbudou nám jen ty pozice uvnitř intervalu.A jak si toto pomocné pole spočítat? Velmi podobně tomu, jak jsme počítali výsledek při jednoduchém řešení. Vypravíme se od levého konce a pokaždé, když bude aktuální znak stejný, jako předchozí, zvětšíme si průběžný počet o jedna. A v každém kroku si aktuální průběžný součet uložíme.
Proč to funguje, je vidět z vysvětlení v druhém odstavci. Pomocné pole nám zabere lineární množství paměti s velikostí vstupní posloupnosti. Co se týče času, pak předvýpočet je lineární s délkou posloupnosti na vstupu (projdeme jej jednou zleva doprava a v každém políčku uděláme konstantní množství práce). Jeden dotaz zodpovíme v konstantním čase, protože jen odečteme dvě čísla.
26-1-4 Oprava databáze (Zadání)
Vyřešme nejprve jednodušší variantu, totiž dvojné prvky. Pro každý prvek pk v zadané posloupnosti můžeme vyzkoušet všechny dvojice předchozích prvků pi,pj a ověřit, zda náhodou jejich součet není pk. Tím dostaneme řešení s časovou složitostí O(n3). To ale není nejlepší řešení této úlohy.
Můžeme si všimnout, že zbytečně několikrát provádíme stejné součty. Co kdybychom si místo toho dané součty systematicky pamatovali a pak v nich jen vyhledávali? To můžeme udělat například binárním vyhledávacím stromem.
V něm si budeme uchovávat všechny možné součty dvojic prvků před aktuálním prvkem pk. Tedy v moment zpracovávání prvku pk v něm bume mít hodnoty součtů dvojic pi,pj pro i,j<k. Takže jen ověříme, zda je hodnota pk obsažená ve stromě a pokud ano, tak pk je dvojným prvkem. Nakonec přidáme do stromu všechny součty pk + pi pro i<k a pokračujeme prvkem pk+1.
Toto řešení má časovou složitost O(n·(log n + n log n)) = O(n2 log n) a paměťovou složitost O(n2).
Nyní pojďme vyřešit úlohu pro trojné prvky. Postupovat budeme velmi podobně. Opět budeme mít binární vyhledávající strom uchovávající součty zatím potkaných dvojic, akorát budeme rozdílně zpracovávat prvek pk. Pro něj budeme předpokládat, že je třetím prvkem v součtu a pro všechny j>k ověříme, zda je možné pomocí součtu dvou prvků před pk dostat hodnotu pj - pk.
Pokud ano, tak prvek pj je trojným prvkem. To zjistíme dotazem na binární vyhledávací strom. Pak stejně jako předtím do stromu přidáme všechny součty tvořené prvkem pk a některým předchozím prvkem a přesuneme se s výpočtem na další prvek posloupnosti.
Řešení má časovou složitost O(n2 log n), protože provádíme O(n2)
operací s binárním vyhledávacím stromem. Při programování použijeme knihovní
implementaci binárního vyhledávacího stromu, například v jazyce C++ to je
set z knihovny STL. Celá realizace řešení je pak kratší, než tento slovní
popis. :-)
Medvědí poznámky
Dvojné prvky jde hledat o něco rychleji. Postupně procházíme přes všechna j a zjišťujeme, zda je součet prvku pj s nějakým prvkem nalevo od něj roven nějakému prvku napravo od něj. Za tímto účelem si budeme udržovat dva setříděné seznamy: L bude obsahovat hodnoty ležících nalevo od aktuálního prvku, P ty napravo.
Pro každé j spočítáme Sj = L+pj (seznam vzniklý přičtením pj ke každému prvku z L). To je také setříděný seznam, takže jeho sléváním s P můžeme snadno zjistit, zda Sj a P mají nějaký společný průnik, čili dvojný prvek. Všechny tyto operace zvládneme pro jedno j provést v lineárním čase, celkově tedy v O(n2). Paměti spotřebujeme pouze O(n).
Vyhledávací stromy jsou mocná zbraň, kterou je dobré ovládat, ale občas lze věci řešit i jednodušeji. Jako třeba zde. Pro hledání trojných prvků postačí předpočítat si všechny možné součty dvojic, setřídit si je a pro každou hodnotu součtu si zapamatovat její nejlevější výskyt. Pak můžeme namísto ve stromu binárně vyhledávat v této setříděné posloupnosti a podle pozice nejlevějšího výskytu snadno ověřit, zda součet leží před zkoumaným pk, anebo až za ním.
Pokud bychom se ovšem spokojili s algoritmem, který je rychlý v průměru
a ne nutně v nejhorším případě, hodí se místo stromu použít hešovací tabulku
– ta pracuje v průměrně konstantním čase na operaci, čímž se časová složitost
hledání trojných prvků sníží na O(n2). Najdeme ji i v STL pod názvem
unordered_set.
26-1-5 Senzory (Zadání)
Zkoušení všech možností tady moc efektivní nebude. Pojďme úlohu trochu rozebrat, aby se na ni jednodušeji útočilo.
První učiněné pozorování bude následující: můžeme věže rozmístit do řádků a do sloupečků nezávisle. Když se totiž věže ohrožují, tak se ohrožují buď v řádku, nebo ve sloupečku, a naopak pokud je rozmístění věží správné v řádcích i ve sloupečcích, je správné i celkově. Zredukovali jsme si tedy zadání na jeho jednodušší verzi, ve které se věže staví do jednoho řádku, dvě nesmí stát ve stejném sloupci, a každá může stát jenom v nějakém vymezeném intervalu. Vyřešíme tyhle podúlohy pro sloupce a pro řádky zvlášť a výsledky spojíme.
Řešení pomocí systému různých reprezentantů
Jednodušší podúloha je speciální případ hledání takzvaného systému různých reprezentantů. Mějme třeba množiny A = {1, 3, 4}, B = {3, 4, 5}, C = {5, 6}. Systém různých reprezentantů je takové přiřazení prvků množin k jejich množinám, že všechny vybrané prvky jsou různé. Příklad systému různých reprezentantů pro tyto množiny A, B, C je třeba A →1, B →3, C →5 (ale třeba A →3, B →3, C →6 nebo A →5, B →3, C →6 už ne). Obecně se systémy různých reprezentantů dají hledat přes toky v sítích. Vytvoříme si bipartitní graf, ve kterém jedna partita budou prvky množin (1, 3, 4, 5, 6) a druhá budou množiny (A, B, C) a natáhneme hrany s kapacitou 1 mezi prvkem x a množinou M tam, kde x ∈M.
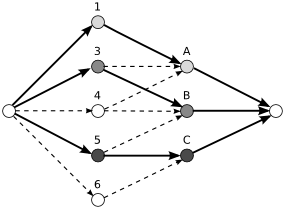
Potom si vytvoříme zdroj, ze kterého povedou hrany kapacity 1 do všech prvků, a stok, do kterého povedou hrany kapacity 1 ze všech množin. V této síti najdeme maximální tok například pomocí Fordova-Fulkersonova algoritmu. Maximální tok nám ukáže hledaný systém různých reprezentantů (pokud existuje). Kapacity hran a podmínky, které musí tok splňovat, zajišťují, že všechny prvky i všechny množiny budou použity maximálně jednou.
Je to zcela správný způsob řešení úlohy o rozmisťování věží. Podrobnosti hledání maximálního toku tu však nenajdete, protože úloha jde řešit jednodušeji a rychleji. Máte-li o ně zájem, můžete je najít v kuchařce o tocích.
Jednodušší řešení
Zkusíme to takzvaně hladově: můžeme nejdříve vybrat věž, kterou umístíme na první sloupeček, pak ze zbylých vybrat tu, kterou umístíme na druhý, a tak dále (samozřejmě přeskakujeme sloupečky bez věží). Jak si ale budeme věže vybírat? Překvapivě tu bude fungovat metoda „do prvního sloupečku vyber tu věž, se kterou jde nejméně hýbat“ (pojmenujme ji třeba minimální věž). To, že takový algoritmus bude fungovat, nahlédneme indukcí.
Důkaz správnosti
Indukci začneme třeba od triviálního případu s jednou věží: tu můžeme umístit hned na první sloupeček, na který může přijít, takže tam algoritmus funguje.
Indukční krok bude schematicky takovýhle: „Když nějaká věž má prázdný interval, je jasné, že žádné řešení neexistuje. Řekněme teď bez újmy na obecnosti, že na první sloupeček jde umístit nějaká věž. Vybereme z věží, které jdou dát do prvního sloupečku, libovolnou minimální, a položíme ji tam. Tím si zmenšíme zadání o jednu věž a jeden sloupeček. Necháme si od indukce přihrát řešení menšího problému. Pokud existuje, přidáme k němu tuhle věž a máme výsledek. Pokud neexistuje, pak neexistuje ani řešení problému včetně minimální věže.“
Zbývá teď dokázat, že pokud budeme věže takhle umisťovat, tak o žádné řešení nepřijdeme. (Důkaz toho, že žádné řešení nepřidáme, je jednoduchý.) Jinými slovy: pokud jdou věže nějak rozmístit podle zadání, tak jdou rozmístit i tak, že v prvním sloupečku bude z věží, které tam šly umístit, libovolná minimální.
Vezměme si nějaké řešení a vyberme si z věží, které můžou dostat první sloupeček, nějakou minimální. Označíme ji třeba M. Nechť M nedostane první sloupeček, ale sloupeček SM. Pokud je první sloupeček v řešení volný, můžeme do něj M přemístit, čímž dostaneme řešení, ve kterém první sloupeček drží vybraná minimální věž. Pokud není první sloupec volný, znamená to, že nějaká věž X jej drží. Protože M je minimální věž, tak interval věže X obsahuje mimo jiné sloupeček SM. Můžeme tedy věže X a M beztrestně prohodit. Po prohození opět dostaneme řešení, které má v prvním sloupci minimální věž.
Implementace
Máme dokázáno, že to bude fungovat, a zbývá to „jenom“ implementovat. Budeme postupně ukrajovat věže a sloupečky. V proměnné si budeme držet poslední sloupeček, do kterého jsme už umístili věž (a další věže budeme umisťovat jenom za něj).
Věže chceme brát v takovém pořadí, abychom pokaždé umisťovali tu, která je v nezpracovaném prostoru minimální. Jak toho dosáhneme? Mohli bychom si v každém kroku najít minimální věž průchodem všech zbylých věží, ale to by nás stálo kvadratický čas. Existuje lepší řešení: ukládat si věže do haldy. Halda konkrétně bude minimová a budeme v ní třídit podle konce intervalu, do kterého můžeme věž umístit. Také do ní věže nebudeme přidávat všechny hned, ale teprve okamžikem, kdy narazíme na začátek jejich intervalu. Kdykoliv z téhle haldy tedy odebereme věž s nejmenším koncem intervalu, bude to právě ta minimální pro sloupeček, který budeme zabydlovat.
Jako první krok věže v O(N log N) setřídíme vzestupně podle minima intervalu. Potom budeme postupně zleva zaplňovat sloupečky a přidávat věže do haldy.
Každou věž zpracujeme takto: jde-li umístit hned za poslední umístěnou věž, učiníme to. Nejde-li to, zkusíme ji umístit na začátek jejího intervalu. Pokud ani to nejde, znamená to, že poslední umístěná věž je za koncem intervalu právě zpracovávané věže, takže zpracovávaná věž nejde umístit nikam – řešení neexistuje. Nakonec nesmíme zapomenout zvýšit proměnnou s poslední umístěnou věží.
A co nás to bude stát? Paměť je jednoduchá: stačí O(N) na uložení vstupu a haldy. Co se času týče: setřídění věží zabere O(N log N). Každou věž také jednou uložíme do haldy a jednou z ní vybereme, což obojí trvá O(log N) za věž, tedy celkem O(N log N). Všechno ostatní trvá kratší dobu.
26-1-6 Hydroponie (Zadání)
Zahrada skýtá přihrádky na rostliny označené čísly 0 až N-1. K dispozici máme M nápajecích okruhů, i-tý okruh je intervalem Ii=[ai,bi)={ai, ai+1, …, bi-1}. Délka intervalu v tomto značení je bi - ai.
Pokoušíme se určit počet všech možných osazení rostlin do přihrádek tak, aby každý interval obsahoval alespoň jednu rostlinu. Protože mohou být výsledné hodnoty extrémně vysoké, počítáme pouze zbytek po dělení této hodnoty číslem 1 000 000 007.
Rozklad na schodiště
Proveďme úvodní pozorování. Platí-li pro navzájem různá i a j inkluze Ii⊆ Ij, můžeme interval Ij ze svých úvah vypustit. Podmínku na obsazení rostliny v tomto intervalu nám zajistí interval Ii.
Dále budeme uvažovat pouze intervaly, které v sobě neobsahují žádný celý interval. Intervaly si navíc uspořádáme vzestupně dle jejich počátku. Pro libovolné i<j budou nyní platit nerovnosti ai<aj a bi<bj. (První nerovnost je dána uspořádáním, druhá tím, že Ij nemůže celý ležet v Ii.)
Získali jsme jakousi schodovitou strukturu. Tuto strukturu si rozebereme na jednotlivá schodiště. Schodiště Si bude množinou intervalů Iu až Iv takovou, že každé dva po sobě jdoucí intervaly mají neprázdný průnik, navíc Si bude vždy největší takovou možnou množinou. Tedy Iu-1 a Iv+1, pokud existují, jsou disjunktní s Iu a Iv. Počet schodišť označme jako T.
Povšimněme si, že úloha se nám nyní rozpadla na T+1 zcela nezávislých podúloh. Pro přihrádky neobsažené v žádném intervalu nejsme ničím vázáni, tedy máme 2K možností jejich obsazení, je-li K počtem těchto přihrádek. Zbývajícími podúlohami jsou jednotlivá schodiště.
Výpočet pro jedno schodiště
Mějme jediné schodiště s intervaly J0, …, Jℓ-1. Nyní označujme Ji = [ai, bi).
Zužitkujeme myšlenku dynamického programování a budeme si postupně počítat hodnoty D(0) až D(ℓ-1), kde D(i) udává počet možných rozmístění květin, umisťujeme-li je pouze do intervalů 0 až i.
Počáteční hodnota D(0) je zřejmě 2|J0|-1, neb nám je zakázáno pouze to obsazení květin v intervalu J0, při kterém neumístíme ani jednu květinu.
Předokládejme nyní, že hodnoty D(0), …, D(i-1) již byly spočteny, a my chceme určit D(i).
Buď p nejmenší takové, že bp > ai. Interval Ji rozdělíme na podintervaly [ai, bp), [bp, bp+1), [bp+1, bp+2), …, [bi-1, bi).
Možnosti osazení květinami si rozdělíme podle toho, do kterého z těchto podintervalů umístíme nejpravější květinu. Nejprve se podívejme na intervaly tvaru [bj, bj+1) pro nějaké j splňující p ≤ j < i. Později se ještě podíváme na speciální interval [ai, bp). Výsledky pro jednotlivé intervaly pak sečteme a získáme D(i).
Máme interval [bj, bj+1), ve kterém bude umístěna alespoň jedna rostlina, a víme, že na pozicích od bj+1 dále už žádná květina nebude. Možností, jak umístit květiny do tohoto podintervalu, je 2bj+1 - bj - 1. Kolika způsoby lze korektně osadit zbytek schodiště udává D(j), což dává celkem (2bj+1 - bj - 1) · D(j) možností pro tento interval.
Zbývá nám interval [ai, bp). Je-li p = 0, pak je mezivýsledkem hodnota 2a0 - ai · (2ai-b0 - 1). Musili jsme obsadit alespoň jednu květinu do intervalu [ai, b0), zbytek intervalu J0 jsme mohli obsadit libovolně.
Pro p > 1 se ještě podíváme na interval Jp-1. Pro ten už platí bp-1 ≤ ai. Počet možných osazení intervalu [ai, bp) je opět 2ai-b0 - 1. Interval [bp-1, ai) lze obsadit libovolně, tedy 2ai-bp-1 způsoby. Jak obsadit všechny pozice před tímto intervalem už udává D(p-1). Celkem tedy (2ai-b0 -1) · 2ai-bp-1 · D(p-1).
Celkový počet možných osazení tohoto schodiště je D(ℓ-1).
Plody našeho snažení
Protože jsou umístění do jednotlivých T schodišť a do přihrádek mimo schodiště nezávislá, získáme výsledek jako součin počtu možností pro tyto jednotlivé případy.
Zbývá se zamyslet, s jakou složitostí umíme celé naše řešení implementovat. Abychom si intervaly správně uspořádali a zbavili se přebytečných, stačí je setřídit a vhodně projít. (Detaily si rozmyslete sami, nebo si je přečtěte ve vzorové implementaci.)
Asymptotická složitost algoritmu bude funkcí dvou proměnných, jmenovitě N a M. V takovém případě nemusí být jednoznačné, která časová složitost je tou optimální. Může to záviset na vztahu mezi těmito proměnnými. (Optimální algoritmus by asi měl podle vstupních hodnot N a M zvolit správnou variantu implementace).
Předvedeme si dvě možné složitosti řešení. V prvním případě intervaly setřídíme v čase O(M log M), třeba pomocí Quicksortu.
Během počítání možností pro všechna schodiště mocníme dvojku a to exponentem z rozsahu 0 až N. Tuto operaci jsme schopni provést v čase O(log N).
Při výpočtu možností pro daný interval ve schodišti sčítáme možnosti podintervalů. Všimněme si, že tento součet není potřeba počítat vždy od nuly, ale stačí jej aktualizovat při zvyšování i a p. To znamená lineární počet operací vzhledem k počtu intervalů. Nejdražší operací je už zmíněné mocnění dvojky.
První řešení má tedy časovou složitost O(M log N) a paměťovou složitost O(M). (Všimněte si, že O(log M) a O(log N) je totéž, protože M je nejvýše N2.)
Protože okraje intervalů jsou z rozsahu 0 až N-1, můžeme je také setřídit přihrádkovým tříděním v čase O(N). Všechny mocniny dvojky si můžeme dopředu předpočítat a pak na dotaz odpovídat v konstantním čase. Tak získáváme druhé řešení s časovou i paměťovou složitostí O(N+M).
Při implementaci nesmíme zapomenout všechny hodnoty průběžně nahrazovat jejich zbytkem po dělení 1 000 000 007, abychom nedostávali ohromná čísla.
Vzorová implementace ukazuje řešení v čase O(M log N).
26-1-7 Mravenci (Zadání)
Pokusme se soustředit na srážku určitých dvou mravenců. Lze si všimnout, že pokud si je neoznačíme, vypadá situace tak, jako by se míjeli a k žádné srážce nedošlo. Mravenec, který spadne z klacku poslední, je tedy ten, který je nejvzdálenější od okraje klacku, ke kterému je otočený. Pozor, takový mravenec je vždy aspoň jeden, ale můžou být i dva!
U druhé části nám přibylo několik těžkostí. Nemůžeme už totiž zanedbat označení mravenců. Nahlédneme ale, že mravenci se na klacku nemohou přeskakovat. Speciálně je tedy prvních n mravenců spadlých z klacku na levé straně totožných s těmi n mravenci, kteří jsou na začátku nejblíže levému konci klacku. Pro pravou stranu platí analogické tvrzení.
Z první části již víme, do jakého směru je na začátku orientován mravenec, jenž spadne jako poslední (pro jednoduchost dále předpokládejme, že doleva, jinak analogicky). Nyní zjistíme počet mravenců, kteří na začátku míří doleva. Řekněme, že je jich k. Pak mravenec, který z klacku spadne jako poslední, je k-tý mravenec zleva v pořadí, v jakém stojí mravenci na začátku.
26-1-8 Turingova strojovna (Zadání)
První tři úkoly byly snadné, čtvrtý trochu těžší. Ukázalo se ale, že všechny čtyři skrývají nečekané hlubiny. Začneme proto snadnými řešeními a pak se spolu vydáme na cestu do hlubin.
Úkol 1
Nejprve si všimneme, že každá neprázdná správně uzávorkovaná posloupnost
obsahuje po sobě jdoucí dvojici (). Smazáním této dvojice vytvoříme
jiné správné uzávorkování, v němž opět najdeme takovou dvojici, a tak dále,
až posloupnost zredukujeme na prázdnou. Naopak začneme-li se špatným
uzávorkováním, smazáním () z něj nikdy nevytvoříme správné. Zjistili
jsme, že správná uzávorkování jsou právě ta, která lze zredukovat na prázdnou posloupnost.
Přesně o to se bude pokoušet náš stroj. Pracovat bude nad abecedou { (, ), * }
a jeho program bude vypadat následovně:
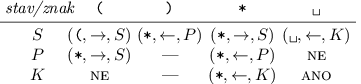
* a přepne se do stavu P, v němž
se bude vracet zpátky a hledat nejbližší levou. Tu také vyhvězdičkuje, načež se
přepne opět do stavu S (všimněte si, že vlevo od aktuální pozice už žádné pravé
závorky nejsou, takže se k nim není potřeba vracet). Až vstupní řetězec dojde, stroj
přejde do stavu K, v němž bude kontrolovat, zda nezbyly nějaké nespárované
levé závorky.
Časová složitost tohoto stroje je O(n2), jelikož až řádově n-krát potřebujeme
najít párovou závorku, což trvá až řádově n kroků. Kvadraticky dlouho bude počítat
například na vstupu (((…))). Kromě prostoru na pásce, kde byl napsán
vstup, nepotřebuje žádnou další paměť.
Úkol 2 s lineární pamětí
Sledujme, jak probíhá výpočet stroje z předchozího úkolu. Vyhvězdičkovaná políčka pásky můžeme ignorovat, ta stroj vždy přeskakuje. Pak platí, že vlevo od aktuální pozice jsou samé levé závorky – to jsou ty, ke kterým jsme ještě nenašli pravou závorku do páru. Každá další závorka je buďto levá (a pak ji přeskočíme, čímž se přesune do levé části), nebo pravá (a tehdy naopak z levé části jednu levou závorku smažeme).
Jinými slovy levou část používáme jako zásobník dosud neuzavřených závorek. Na vícepáskovém stroji si ho můžeme uložit na samostatnou pásku. Tím zařídíme, že další znak v zásobníku bude dostupný v konstantním čase.
Program stroje bude vypadat takto:
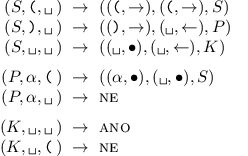
Stroj začne ve stavu S. Na první pásce se bude pohybovat zleva doprava a postupně číst závorky ze vstupu. Na druhé pásce si bude udržovat zásobník otevřených závorek a hlava se v klidovém stavu bude nacházet vpravo od poslední uložené závorky.
Pokud stroj přečte levou závorku, uloží ji na zásobník.
Pokud přečte pravou závorku, přepne se do stavu P a zkontroluje, jestli na zásobníku má nějakou levou. Pakliže ano, odstraní ji a vrátí se do počátečního stavu. Pokud ne, závorkování není správné.
Skončí-li vstup, je ještě potřeba zkontrolovat, že na zásobníku nezůstala žádná neuzavřená závorka. O to se stará stav K.
Tento stroj pracuje v lineárním čase s délkou vstupu (každý znak zpracuje v konstantním čase) a spotřebuje lineárně mnoho prostoru na pracovní pásce.
Úkol 2 s logaritmickou pamětí
Zadání vybízelo k co nejmenší spotřebě paměti. Vskutku, předchozí řešení
prostorem vysloveně plýtvá. Do zásobníku ukládá samé levé závorky, takže
by úplně stačilo pamatovat si jejich počet ve dvojkové soustavě. Uložíme
ho jako posloupnost znaků 0 a 1 na pracovní pásce. Nejnižší
řád se bude nacházet vpravo a v klidovém stavu bude hlava stát na mezeře
napravo od něj.
Obsluha vstupní pásky bude vypadat následovně:
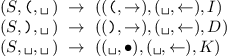
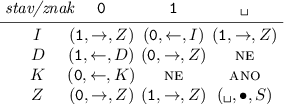
Nyní spotřebujeme pouze logaritmické množství prostoru, neboť dvojkové číslo v rozsahu 0 až n zapíšeme pomocí ⌊ log2 n⌋+ 1 bitů. Ovšem zvyšování a snižování počítadla trvá logaritmicky dlouho, takže jsme si časovou složitost pokazili na O(n log n).
Úkol 3
Pokud si můžeme dovolit přidávat pásky, vystačíme si dokonce s jediným stavem. Rozšíříme abecedu o tolik symbolů, kolik měl původní stroj stavů. Přidáme novou pásku, z níž budeme používat jen jediné políčko. Na něm budeme udržovat informaci o tom, jaký stav původního stroje právě simulujeme. A aby se nový stroj správně rozběhl, určíme, že prázdné políčko odpovídá počátečnímu stavu původního stroje.
Úkol 4
Na jednopáskovém stroji se nabízí rozšířit abecedu na uspořádané dvojice (z,s), kde z je znak původní abecedy a s stav původního stroje. Jenže: pokud posuneme hlavu na sousední políčko, musíme tam přenést informaci o stavu, která byla zakódovaná do stávajícího políčka. To nejde udělat najednou (protože do stavu nového stroje zakódujeme jen 1 bit informace), ale s trochou šikovnosti poskytují dva stavy dost manévrovacího prostoru na to, abychom informaci přenesli po částech.
Stavy nového stroje nazveme X a Y. Abecedu rozšíříme na trojice (z,s,m), přičemž z a s budou odpovídat znaku a stavu původního stroje (stavy očíslujeme) a m bude mód, na němž bude záviset, co zrovna X a Y znamenají. Módů budeme rozeznávat pět: klid, vysílání doprava, vysílání doleva, příjem zprava, příjem zleva.
Představme si, že nový stroj právě odsimuloval jednu instrukci starého stroje. Na aktuálním políčku změnil s i z a teď se potřebuje posunout na sousední políčko, řekněme doprava. Udělá toto:
- Na aktuální políčko zapíše mód vysílání doprava, přepne se do stavu X a posune hlavu doprava.
- Sousední políčko bylo v módu klid, takže si stav X vyloží jako požadavek, který přišel zleva. Nastaví s=0, přejde do módu příjem zleva a ve stavu X se posune zpět doleva.
- Nyní je předávání informací nastartováno. Vysílací políčko pokaždé sníží své s o 1 a dokud nevyjde 0, přesouvá se na přijímací políčko ve stavu X. Přijímací políčko zvýší své s o 1 a vrátí hlavu zpět (stále stav X). Pokračujeme v předávání.
- Jakmile vysílací políčko dopočítá do nuly, přepne svůj mód na klid a posune hlavu na přijímací políčko, tentokrát ve stavu Y. Podle toho přijímací políčko pozná, že přenos je u konce, a odsimuluje další instrukci původního stroje.
Pokud chceme přenášet informaci doleva místo doprava, postupujeme obdobně, jen v prvním kroku použijeme stav Y, podle čehož přijímací políčko pozná, že přenášíme zprava.
Každou instrukci původního stroje tedy umíme odsimulovat konstantně mnoha instrukcemi stroje nového.
Úkol 4: start výpočtu
 Právě předvedené řešení 4. úkolu má jeden malý, leč podstatný háček:
jak se vlastně celý výpočet rozběhne? Potřebujeme přeci, aby byl ve znaku
na prvním políčku pásky zakódován počáteční stav S0 původního stroje.
Právě předvedené řešení 4. úkolu má jeden malý, leč podstatný háček:
jak se vlastně celý výpočet rozběhne? Potřebujeme přeci, aby byl ve znaku
na prvním políčku pásky zakódován počáteční stav S0 původního stroje.
Jak to zařídit? Máme možnost určit pro každý znak původní abecedy, jaká trojice mu bude odpovídat v nové abecedě, a také si můžeme vybrat počáteční stav nového stroje.
Hned se nabízí zapisovat znaky původní abecedy jako trojice (z,S0,klid). Jenže ani pro počáteční stav X, ani pro Y to nedopadne dobře: stroj se bude snažit kopírovat stav ze sousedního políčka, které na to vůbec není připraveno. Tak raději necháme nový stroj, ať svůj výpočet zahájí zapsáním stavu S0. Jak ale pozná, kdy to má udělat?
Půjdeme na to menší oklikou. Nejprve si rozmyslíme, že každý Turingův stroj můžeme předělat tak, aby nikdy nevyužíval políčka pásky nalevo od počáteční polohy hlavy (tedy aby jeho páska byla jen jednostranně nekonečná). Zařídíme to „přeložením pásky napůl“. Políčka původní pásky si očíslujeme … , -3, -2, -1, 1, 2, 3, … a na i-té poličko nové pásky uložíme uspořádanou dvojici znaků z původních políček i a -i.
Předělaný stroj bude simulovat instrukce původního stroje a navíc si bude ve svém stavu pamatovat, zda se nachází v kladné či záporné části původní pásky. Podle toho bude používat buď první, anebo druhou složku dvojice a případně obracet směr pohybu hlavy. Navíc si na políčko 1 umístíme značku, abychom poznali, že jsme přešli přes rozhraní kladné a záporné části.
Tato transformace zpomalí výpočet pouze konstanta-krát a má jeden příjemný důsledek, kterého vzápětí využijeme: vstoupíme-li na jakékoli políčko poprvé, je to vždy zleva.
Nyní se vraťme zpět k redukci počtu stavů. Každý znak z původní abecedy zakódujeme jako trojici (z,S0,init). Nový mód init se chová stejně jako klid a navíc říká, že jsme na políčku poprvé. Proto víme, že během výpočtu nového stroje nemůžeme na takové políčko přijít ve stavu Y (ten by totiž znamenal „jdeme kopírovat zprava“). Y tedy prohlásíme za počáteční stav nového stroje a kombinaci mód init + stav Y využijeme k rozjezdu stroje.
Heuréka, problém vyřešen. Každý jednopáskový Turingův stroj umíme upravit tak, aby počítal totéž (až na změnu abecedy), zpomalil se jenom konstanta-krát a vystačil si přitom s pouhými dvěma stavy. (Přesněji řečeno, předvedli jsme to pro stroje, které odpovídají stavem ano nebo ne. Pokud by výstup vydávaly na pásce, museli bychom ještě na závěr výpočtu pásku „vyčistit“ a překódovat zpět do vstupní abecedy. Ale to už je maličkost.)
Pro přehlednost ještě ukážeme tabulku, co který stav znamená ve kterém módu:

Poznámka: Dodejme ještě, že inicializaci lze provést i jinak. Využijeme toho, že jsme ve vysílacích módech nepotřebovali stav Y. Pojďme i tam stavem rozlišovat, zda jsme přišli zleva nebo zprava. Navíc máme možnost v každém módu poprohazovat, co znamená X a co Y. Pak zafunguje následující trik.
Na počáteční políčko přijdeme ve stavu X, takže si políčko myslí, že má přijímat zleva. Požádá proto políčko vlevo od sebe o pokračování vysílání. Jenže levé políčko o žádném vysílání neví, takže to interpretuje jako žádost o příjem zprava. Přejde tedy doprava s žádostí o vysílání. Můžeme zařídit, aby si pravé políčko tuto žádost vyložilo jako konec vysílání, čili přijalo stav 0. Ten zpracujeme speciálně: skočíme doleva a také předáme konec vysílání. I levé políčko ukončí příjem přijetím stavu 0, ale umí to rozlišit, protože přišel zprava, takže ho může zpracovat jinak speciálně: zahájením přenosu skutečného počátečního stavu stroje doprava. Kouzlo se zdařilo.
Zpět k úkolu 1: rychlejší řešení
Trik s počítadlem z úkolu 2 se dá využít i na jednopáskovém stroji. Jen si musíme dát pozor, kam počítadlo uložíme: pokud na začátek pásky (před vstup), budeme ke konci vstupu potřebovat spoustu kroků na přesuny mezi vstupem a počítadlem; počítadlo za koncem vstupu se bude chovat podobně špatně na začátku výpočtu. Kam tedy? Pořídíme si počítadlo stěhovavé: bude umístěno těsně před dosud nezpracovanou částí vstupu a po zpracování každé další závorky ho celé přestěhujeme o jednu pozici doprava.Program stroje bude vypadat následovně:
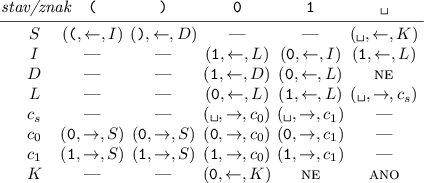
Stroj opět začíná ve stavu S. Jakmile zmerčí levou závorku, posune se těsně před aktuální pozici, kde je uloženo počítadlo, a začne ho inkrementovat. Přitom setrvává ve stavu I, dokud dochází k přenosu do vyšších řádů. Jakmile přenosy ustanou, přejde do L a pohybuje se směrem k levému okraji počítadla. Nakonec pomocí stavů c0, c1 a cs celé počítadlo přesune o znak doprava a vrátí se zpět do S.
Podobně reaguje na pravou závorku, jen k tomu používá dekrementovací stav D. Na konci výpočtu jako obvykle pomocí stavu K zkontroluje, že počítadlo vyšlo nulové.
Časová složitost tohoto řešení je O(n log n), protože pro každý znak vstupu strávíme O(log n) kroků zvyšováním či snižováním a následně přesunem logaritmicky dlouhého počítadla. Paměti zabíráme stále O(n).
Zpět k úkolu 2: trocha naděje
 Také vám vrtá hlavou, jestli by nešlo nějak zkřížit naše dvě řešení
druhého úkolu a dosáhnout současně lineárního času a logaritmické paměti?
Jistá naděje tu je.
Pozorujme, jak se mění číslice počítadla, když ho opakovaně inkrementujeme:
Také vám vrtá hlavou, jestli by nešlo nějak zkřížit naše dvě řešení
druhého úkolu a dosáhnout současně lineárního času a logaritmické paměti?
Jistá naděje tu je.
Pozorujme, jak se mění číslice počítadla, když ho opakovaně inkrementujeme:
| 0000 →0001 →0010 →0011 →0100 →0101 →0110 → | |
| →0111 →1000 →1001 →1010 →1011 →… |
Pro přehlednost jsme změněné číslice vyznačili tučně.
Pokaždé se jedničky na konci čísla změní na nuly a nula před nimi na jedničku. Nebo jinak: jedna jednička vznikne a možná nějaké zaniknou. Pokud provedeme m inkrementů, vzniklo celkem m jedniček. Každá z nich zanikla nejvýš jednou, takže všech zániků dohromady je také nejvýš m. Všech m inkrementů tedy zabralo čas O(m).
Tehdy říkáme, že jeden inkrement má konstantní amortizovanou časovou složitost. Hezky se to popisuje pomocí penízkové metody. Jelikož čas jsou jak známo peníze, zavedeme mezi nimi směnný kurs. Jeden penízek bude představovat dostatek času na provedení jedné operace našeho stroje: tedy přepsání nuly na jedničku či opačně, včetně případného pohybu hlavy.
Nyní prohlásíme, že na provedení jednoho inkrementu po uživateli chceme 2 penízky. Jeden z nich použijeme na vytvoření jedničky, druhý dáme nově vzniklé jedničce do vínku a ona si z něj časem zaplatí své smazání. Za m inkrementů tedy zaplatíme 2m penízků a každou operaci stroje jsme naúčtovali některému z inkrementů.
Dokud tedy při kontrole závorek potkáváme jen ty levé, časová složitost
stroje je lineární. Jenže… pravá závorka způsobí snížení počítadla
a to nám celý elegantní amortizační argument zboří: počítadlo může libovolně
dlouho střídat hodnoty 0111… 1 a 1000… 0, což nutně
zabere logaritmický čas.
Úkol 2: dvojková soustava vrací úder
Tak snadno se přeci nevzdáme. Dvojkovou soustavu rozšíříme, aby byla vyvážená. Vedle číslic 0 a 1 použijeme navíc -1 (pro zkrácení zápisu budeme místo 1 psát+ a místo -1 prostě -).
Váhy řádů budou stále mocniny dvojky, takže číslo ckck-1… c1c0
bude mít hodnotu ∑| k |
| i=0 |
Dvojkový zápis čísla funguje i ve vyvážené dvojkové soustavě, ale totéž
číslo může mít i jiné zápisy. Například 6 (110 dvojkově) se dá zapsat jako
++0, ale i +-+0 nebo +-0-0, jakož i mnoha dalšími způsoby.
Přesto z první číslice poznáme, zda je číslo kladné nebo záporné.
Nechť první číslice je + a má váhu 2k. Potom ani
kdyby byly všechny ostatní číslice záporné, nepřispějí dohromady tolik, aby se
celé číslo vynulovalo, nebo dokonce přehouplo do záporna. Platí totiž
20 + 21 + … + 2k-1 = 2k - 1. Podobně je-li první číslice -,
musí být číslo nutně záporné.
Z toho speciálně plyne, že jediné možnosti, jak zapsat nulu, jsou řetězce
číslic 0. Cokoliv jiného je buď kladné, nebo záporné.
Inkrementování čísla provedeme takto: půjdeme zprava doleva. Pokud potkáme 0,
změníme ji na + a zastavíme se. Potkáme-li -, změníme ho na 0
a zastavíme se. Narazíme-li na +, přepíšeme ho na 0 a stejně jako
v klasické dvojkové soustavě provedeme přenos do vyššího řádu (o číslici vlevo).
Dekrementování je symetrické: z 0 uděláme -, z + uděláme 0,
z - vytvoříme 0 a přenos.
Posloupnost inc, inc, inc, inc, dec, dec, inc tedy projde hodnotami
0,
+,
+0,
++,
+00,
+0-,
+-0,
+-+.
Nyní nahlédneme, že inkrementování i dekrementování má konstantní amortizovanou
složitost. Penízky budeme tentokrát přiřazovat všem nenulovým číslicím. Inkrementování
si nechá od uživatele zaplatit 2 penízky. Pokud přepíše 0 na +,
zaplatí to z uživatelova penízku a ten druhý dá do vínku vzniklému +.
Změní-li + na 0, zaplatí to z penízku toho + a pokračuje
ve výpočtu. A pokud přepíše - na 0, zaplatí to z penízku toho -
a dva uživatelovy penízky může prohýřit. Dekrementování se chová obdobně, též si
vystačí se dvěma penízky.
K vyřešení úlohy použijeme Turingův stroj, který bude fungovat obdobně jako naše předchozí řešení s dvojkovým počítadlem, jen použijeme vyváženou dvojkovou soustavu. Popíšeme jen obsluhu počítadla, zbytek stroje zůstane stejný. V klidovém stavu budeme opět udržovat hlavu vpravo od počítadla. Navíc aby se nám snadno testovala nulovost počítadla, budeme nevýznamné nuly ze začátku čísla při každé příležitosti mazat.
Program stroje vypadá takto:
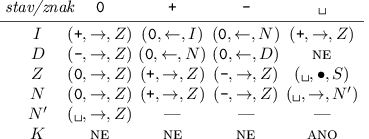
0, odskočí si ještě
do stavu N, v němz zkontroluje, zda tato nula neleží na začátku čísla, a případně
ji smaže. Stav K slouží k závěrečné kontrole nulovosti počítadla – jelikož
nevýznamné nuly průběžně mažeme, postačí testovat prázdnost pásky.
Dosáhli jsme tedy lineární časové a logaritmické prostorové složitosti. Na závěr dodejme, že logaritmický prostor je skutečně zapotřebí, ale důkaz je trochu pracnější a do okraje této stránky by se nevešel ☺
Úkol 2: kočkopsí řešení
Ukážeme ještě jedno optimální řešení druhého úkolu. Je technicky pracnější, ale myšlenkově prostší: Šikovně zkřížíme první řešení (počítadlo v jedničkové soustavě, lineární čas, lineární paměť) s druhým (dvojková soustava, čas O(n log n), paměť O(log n)).
Opět budeme udržovat počítadlo rozdílu levých a pravých závorek. Počítadlo bude dvojkové, ale budeme ho aktualizovat po skocích. Nejprve spočítáme ℓ=⌈ log2 n⌉.
Vstup budeme zpracovávat po blocích velikosti ℓ. Pro každý blok budeme udržovat počítadlo v jedničkové soustavě. Zajímat nás bude jeho hodnota na konci bloku a také nejnižší záporná hodnota během bloku. To vše zjistíme v čase O(ℓ) a prostoru taktéž O(ℓ).
Hodnotu počítadla na konci bloku převedeme do dvojkové soustavy a přičteme ji ke globálnímu počítadlu. Před tím ještě ověříme, že nejnižší záporná hodnota nepřesáhla předchozí hodnotu globálního počítadla. Všechny tyto operace stihneme v O(ℓ) – tolik bitů mají dvojková čísla, s nimiž pracujeme. Převod z jedničkové do dvojkové soustavy zařídíme postupným přičítáním jedničky, které, jak už víme, trvá O(1) amortizovaně.
Každý blok tedy zpracujeme v čase O(ℓ) a prostoru O(ℓ). Všech O(n/ℓ) bloků v čase O(n) a prostoru opět O(ℓ) = O(log n).