Druhá série dvacátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Zadání úloh
V předchozí sérii jste mohli sledovat nouzové přistání vesmírné
lodi Freya. Jacob, který přistání přežil, nalezl kus od lodi
zdobený oštěp, známku inteligentního života. Vyrazil ho hledat.
Najednou ho ale vyrušilo zapraskání za jeho zády …
* * *
Mezi listy zlatě zasvítily dva velké kruhy. Byly to oči nějakého zvířete.
K očím patřil i čumák a překvapivě malá hlava. A tělo a čtyři dlouhé nohy.
Jacobovi vyskočilo srdce někam do krku.
Nedělal si iluze o tom, že zvíře přišlo, aby se stalo jeho průvodcem
po neznámé planetě. Když jako jediný přežijete nouzové přístání vesmírné
lodi, je to samo o sobě dost šílené a na další zázrak si obvykle musíte
zase chvíli počkat.
Zvíře zatím Jacoba pozorovalo. Možná pozorovalo i kus jeho okolí.
Rozhodně se zdálo, že pozorně naslouchá. Aspoň pokud to, co Jacob
považoval za uši, skutečně byly uši. Něco tu nesedělo, ale
strach nedovolil jeho mozku zabývat se nějakými nepodstatnými
nesrovnalostmi. Místo toho se dal na útěk.
Běžel, co mu síly stačily, a litoval, že se nedá vylézt na okolní stromy.
Netušil, jestli zvíře zůstalo stát na místě, nebo jestli běží za ním a on
ho jen pro svůj vlastní dusot neslyší. Netroufal si ohlédnout se, a navíc,
dokud zvíře neviděl, mohl doufat, že tam není.
Najednou vzduch prořízlo nějaké zasvištění. Ani tehdy se Jacob neohlédl,
jen si uvědomoval, že ho nic neskolilo, že může běžet dál.
Zastavil se až za hodnou dobu, kdy začal opadávat jeho strach, a s tím
mu začaly docházet síly. Našel odvahu ohlédnout se. Po zvířeti nebylo ani
vidu. Jacob si nebyl úplně jistý, že trefí zpět, ale pro tuhle chvíli
se rozhodl doufat, že cestu najde.
Začal se zase soustředit na svůj původní plán, totiž hledat místní
inteligentní život. Pozorně se rozhlédl po okolí. A zděsil se.
Teprve teď si všiml, že kus od něj jsou volně natažené dva provazy,
které se do sebe navíc poněkud zamotaly. Byl div, že se o ně při svém
úprku nepřerazil. Jacob se k nim sehnul, aby je mohl prozkoumat blíž.
26-2-1 Zamotané provazy (7 bodů)
V pralese jsou volně natažené dva provazy, které se do sebe zamotaly.
Provazy jsou pevně uvázané na dva stromy, první provaz níž a druhý
výš. Žádný z nich se nikde nevrací. Může to tedy vypadat třeba takto:
O každém překřížení víme, který z provazů je vpředu.
Chceme zjistit, jestli je možné provazy rozmotat bez toho, aby bylo
nutné některý z nich odvazovat.
Program dostane na vstupu číslo N udávající počet křížení a N
čísel 1 nebo 2 udávajících, který provaz je vpředu (na stromech
je provaz 2 vždy uvázaný nad provazem 1). Odpovědět má ano,
nebo ne, podle toho, zda je provazy možné rozmotat.
Příklad (odpovídá obrázku):
4
1 2 2 1
Odpovědí je
ano, jelikož provazy rozmotat jdou.
Řešení
Při zkoumání provazů Jacob najednou zahlédl mezi stromy jakýsi barevný
záblesk. Pouhým pohledem se mu nedařilo zjistit víc, a tak se
s patřičnou obezřetností vydal tím směrem. Jak se přibližoval, měnily
se občasné záblesky v barevnou plochu prosvítající mezi stromy.
Konečně se Jacob dostal až k ní. Ocitl se na něčem, co snad mohlo
připomínat mýtinku, ovšem po stromech ani trávě tu nebyly vůbec
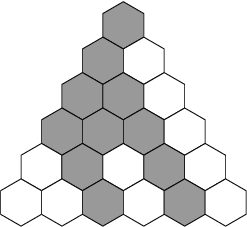
žádné stopy. Teď už Jacob viděl, že trojúhelníkovou barevnou plochu
tvoří zvláštní hexagonální kameny, některé červené, některé do žluta.
Zdálo se, že je kdosi naskládal do mnoha vrstev, kterými pečlivě
vyplnil hlubokou jámu; několik dalších kamenů se válelo v nejbližším
okolí. V jednom z nich byl vyrytý podivný nápis:
Jacob si všiml, že jedna z barev spojuje všechny tři strany
trojúhelníku, a napadlo ho, jestlipak je to tak i ve vrstvách,
které nevidí.
26-2-2 Barevný trojúhelník (8 bodů)
Máme rovnostranný trojúhelník o hraně N tvořený hexagonálními kameny dvou barev.
Dokažte, že v trojúhelníku existuje jednobarevná souvislá plocha,
ve které se nachází alespoň jeden kámen z každé strany trojúhelníku.
Kameny ve vrcholech patří do dvou stran zároveň.
Příklad takového trojúhelníku si můžete prohlédnout na obrázku.
Barvou, která spojuje všechny tři strany, je zde šedá.
Řešení
Protože se začalo připozdívat, rozhodl se Jacob brzy pokračovat dál.
Kamenný trojúhelník mu nyní sloužil jako dobrý orientační bod, a on
se vypravil směrem dál od jednoho z jeho vrcholů.
Po nějaké době došel k místu, kde se prales najednou začal rozestupovat.
Vzniklý výhled odhalil krom jiného to, že tato část pralesa je
mírně vyvýšená nad okolím – zdola musel být nahoru opravdu impozantní
pohled.
O kus dál uviděl Jacob řeku. To ho potěšilo, neboť pokud se tu dá
spoléhat na podobné věci jako na Zemi, mohl by ji sledovat a dojít
po jejím proudu k nějaké civilizaci.
Zdálo se ovšem, že terén je všelijaký a některá místa by mohla
cestu hodně zpomalit. Musel si ji proto dobře rozmyslet.
26-2-3 Plánování cesty (10 bodů)
Jacob se chce co nejrychleji dostat k řece. Terén, přes který musí
projít, si lze představit jako čtvercovou síť o rozměrech R ×S.
V některých oblastech je tento terén dost nepříjemný, a tak přes
některá políčka trvá průchod delší dobu, některá jsou dokonce
zcela neprůchozí.
Průchod přes oblast ležící na souřadnicích i, j trvá ti, j.
Přecházet mezi políčky je možné pouze vodorovně nebo svisle (šikmo ne).
Vaším úkolem je najít nejrychlejší cestu.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Jacob cestu naplánoval, jak nejlépe uměl. Dál byl ovšem rozhodnutý vyrazit
až ráno. Přeci jen není nejrozumnější pohybovat se unavený někde, odkud
můžete spadnout. Teď si raději opatřil provizorní přístřešek. Chvíli se
ještě podivoval nad tím, jak jasná je noc, a pak se uložil ke spánku.
* * *
Ráno se Jacob vzbudil brzy. Pobalil si svých několik věcí a odhodlaně
vyrazil na cestu. Terén tu byl skutečně všelijaký, místy příjemně
ušlapaná hlína, místy skoro bažiny, mezitím ledacos jiného, ovšem
připravená trasa se vcelku osvědčila. Mohlo být krátce po poledni,
když Jacob dorazil k řece.
V jednom kameni u břehu byl opět vyrytý podivný nápis:
Ještě víc ovšem Jacoba zaujaly podivné kostky na protějším břehu.
Vypadaly trochu jako dětské dřevěné kostičky, jen o mnoho větší.
A zdálo se, že z nich někdo chce podobně jako z kostiček pro děti
postavit velkou věž.
26-2-4 Stavba věže (10 bodů)
Někdo se z K kostek snaží postavit věž. Všechny kostky jsou stejně
velké, ale každá kostka má svoji váhu wi a nosnost ℓi.
Nosnost ℓi znamená, že i-tá kostka unese na ní stojící kostky
o maximální celkové váze ℓi, jinak se zbortí a věž spadne.
Zajímá nás, jestli lze postavit věž ze všech K kostek. Věž stavíme
tak, že přímo na sebe pokládáme jednotlivé kostky (můžete si představit
i to, že stavíme komín).
Lehčí varianta (za 3 body): Vyřešte úlohu za předpokladu, že všechny kostky
mají váhu w = 1.
Řešení
Stavba, ať už měla být v budoucnosti čímkoli, byla zrovna opuštěná.
Jacob se tedy vydal dál po proudu řeky. Cestou občas potkal nějaký ten
nápis na kameni, stále se mu v nich ale nedařilo odhalit žádný smysl.
Po několika nápisech a mnoha krocích se před Jacobem najednou objevila
malá věžička. Nebo alespoň malá na místní poměry. Jak už Jacob očekával,
stál před ní kámen s nápisem:
Věžička neměla okna, měla ovšem dveře. Po troše váhání si Jacob dodal
odvahy a zkusil dveře otevřít. Šlo to překvapivě lehce. Jako první
zaznamenal směs různého hučení a bzučení. Pak teprve s jistou
úlevou zjistil, že vevnitř nikdo není.
Původcem podivných zvuků se ukázaly být jakési krabičky. Byly na sobě
různě zavěšené, celá konstrukce byla navíc uchycená ve věžičce.
Jacob se ale nemohl ubránit dojmu, že konstrukce už nemůže dlouho
vydržet. Ačkoli si nebyl jistý, jestli je to dobrý nápad, rozhodl se
jí pomoci tím, že ji vyváží.
26-2-5 Vyvažování (12 bodů)
Očíslované krabičky jsou zavěšené ve věžičce, hrozí ale,
že celá konstrukce spadne. Chceme ji proto vyvážit. Podle piktogramů
na zdech víme, že je potřeba zachovat určité pořadí krabiček
na konstrukci. Celou úlohu si tak můžeme představit jako vyvažování
binárního vyhledávacího stromu.
Na vstupu máme obecný binární vyhledávací strom (jeho definici
naleznete v kuchařce) a chceme z něj udělat dokonale vyvážený binární
vyhledávací strom. Pro každý vrchol výsledného
stromu tedy musí platit, že rozdíl velikostí jeho levého a pravého
podstromu je nejvýše 1.
Konstrukce už drží jen silou vůle, takže požadujeme, aby váš
algoritmus pracoval s lineární časovou složitostí.
Počet bodů, které dostanete, bude záviset na prostorové (paměťové)
složitosti vašeho řešení. Nějaké body dostanete i za lineární, na
plný počet ale potřebujete konstantní složitost.
Řešení
Po práci si Jacob udělal pauzu na svačinu. Bylo pomalu vhodné
začít myslet na návrat, ale on chtěl ještě pokračovat ve svém pátrání.
Usoudil, že alespoň do večera může jít dál, a pak se uvidí.
S plnějším žaludkem se pak Jacob vypravil opět po proudu řeky. Tentokrát
ovšem potkal něco zajímavého mnohem dřív. Došel totiž k něčemu, co se
snad dalo považovat za brod.
Tradičně tu potkal vyrytý nápis, tentokrát dost složitý. Po chvilce
jeho zkoumání Jacob pojal podezření, že znaky, které už nějakou dobu
potkával na kamenech u břehu, jsou zkratkou nějakého názvu. Studoval
další slova na kameni a přemýšlel, která z nich by také mohla být
názvy a mít nějakou svoji zkratku.
26-2-6 Zkratky míst (12 bodů)
Máme podezření, že pro názvy míst se používají třípísmenné zkratky,
a máme také seznam slov, o kterých si myslíme, že by mohly být názvem
nějakého místa.
Zkratka má první písmeno vždy stejné, jako je první písmeno názvu
daného místa, a zbylá dvě písmena jsou libovolná dvě písmena z názvu
místa ve správném pořadí. Název Praha tak lze zkrátit např.
na PRH nebo PHA, ale už ne na PHR nebo RHA.
Vaším úkolem je zjistit, pro která všechna slova bychom skutečně
uměli takovou zkratku najít. Zkratky míst musí být navzájem
jedinečné, chceme jich ale najít co nejvíce.
Je-li možných řešení se stejným počtem nalezených zkratek víc,
vypište libovolné z nich.
Příklad:
Vstup: Výstup:
Pra Pra PRA
Praga Praga PAA
Prak Prak PAK
Prk Prk PRK
Prkg Prkg PRG
Pak Prague PGU
Prague
Řešení
Jacobovi se povedlo překonat řeku a dostat se na druhý břeh. Před ním
začínalo něco, co silně připomínalo cestičku. Zhluboka se nadechl
a pak po ní vyrazil.
Cestička chvíli vedla skoro podél řeky, pak se od ní ovšem prudce
odklonila a zavedla Jacoba za hradbu stromů. Nebyly to stejné stromy
jako v pralese, ale podobně jako ony byly vysokánské a měly o trochu
jinou barvu, než by člověk čekal na Zemi.
Jacob se rozhlédl kolem sebe a bezděky zatajil dech. Našel, co hledal!
Byl tu inteligentní život, byl tady, přímo před ním.
Tvorové byli vlastně podobní lidem. Byli vyšší, Jacob by vedle nich
vypadal jako malé dítě. Podobně jako zvíře minulý den měli
překvapivě malou hlavu a naopak nezvykle velké oči. Barvou kůže
připomínali spíše pozemšťany, kterým zrovna není dobře od žaludku.
Ale bez nejmenších pochyb to byli představitelé místního inteligentního
života.
Skupinka tvorů se zrovna motala kolem obrovského kmene stromu, který
zřejmě pocházel z pralesa.
26-2-7 Čištění kmene (13 bodů)
Humanoidní tvorové čistí kmen stromu. Celkem se práce účastní T tvorů.
Na kmeni je M míst, která je potřeba očistit. Každé takové místo je na
nějaké pozici mi (to může být třeba vzdálenost od konkrétního konce
kmene; pozice bude vždy celočíselná).
Na začátku stojí j-tý tvor na pozici tj. Práce tvorů probíhá
v jednotlivých krocích: v každém kroku se každý tvor (nezávisle na
ostatních) může přesunout o jednu pozici vlevo, vpravo, nebo může
zůstat stát na místě.
Očištění části kmene, nad kterou tvor stojí, je bleskové (proběhne
ve stejném kroku, kdy tvor k této části kmene dojde). Speciální
výjimkou je počáteční pozice každého tvora. Ta je očištěná ještě
před tím, než tvor udělá první krok.
Zajímá nám nejmenší počet kroků potřebný k očištění celého kmene.
Při řešení můžete předpokládat 1 ≤ M, T ≤ 100 000 a
1 ≤ mi, tj ≤ 1 000 000 000.
Příklad:
Mají-li se zkontrolovat místa 2, 5, 6 a tvorové stojí na pozicích
3, 5, zvládnou kmen očistit na 1 krok. Kdyby stáli na 3, 4,
budou kroky potřebovat 2.
Řešení
Když se před ním tvorové vynořili, nebyl si Jacob najednou vůbec jistý,
co by vlastně měl udělat. Pozoroval skupinku, všiml si také kdesi za
nimi ďolíků v zemi, všiml si, že v jednom z nich zmizel stejný tvor.
Najednou se ozval výkřik. Jacob se polekaně rozhlédl. Někdo si ho
zřejmě všiml a upozornil na něj ostatní. V té chvíli se na něj upřely
pohledy všech tvorů.
Pokračování příště…
První Jacobovy kroky po neznámé planetě s vámi sledovala
Karolína „Karryanna“ Burešová
26-2-8 Továrna na přepisování (14 bodů)
V prvním díle letošního seriálu jste se mohli seznámit s Turingovými stroji coby
zajímavým teoretickým modelem počítače. Dnes v naší zoo výpočetních
modelů popojdeme k sousednímu výběhu, kde se pasou přepisovací pravidla.
Ne nadarmo jsou hned vedle – časem uvidíme, že si spolu tahle dvě zvířátka
náramně rozumějí.
Abeceda a vstup s výstupem
Jak už název napovídá, přepisovací pravidla pracují nad nějakým zadaným
řetězcem znaků (říkejme mu vstup) a postupně ho nějak přepisují, až
dostanou nějaký další řetězec znaků (výstup). Než začneme mluvit
o samotných pravidlech, pojďme tyto řetězce pořádně definovat.
Za abecedu budeme označovat konečnou množinu všech znaků, které se mohou
vyskytnout v řetězci. Vstup a výstup jsou pak vždy nějaké konečné
řetězce znaků z této abecedy.
Mimo to zavedeme dva metaznaky, kterými budeme označovat okraje řetězce:
^ na začátku a $ na konci řetězce. Tyto znaky nebudou součástí
abecedy, a tedy se nebudou vyskytovat nikde jinde než právě na okrajích řetězce. (Podobnost s regulárními výrazy používanými v praxi vůbec není náhodná.
Chcete vědět víc? Nahlédněte do seriálu 23. ročníku.)
Abecedou mohou být například čísla 0-9, písmena a-z, nebo třeba { ♥, ♠, ♣, ♦}.
Jednotlivé úlohy pak mohou navíc určit, že ve vstupu nebo výstupu se smí
vyskytovat jen některé znaky abecedy.
Přepisovací pravidla
Každé přepisovací pravidlo má svou levou a pravou část: levé části budeme říkat
vzor a pravé přepis. Zapisovat ho budeme takto:
vzor →přepis
Ve vzoru se mohou kromě znaků abecedy vyskytovat
i metaznaky začátku a konce řetězce (pak se vzor váže k nějakému z okrajů
řetězce), v přepisu se už mohou vyskytovat jen znaky abecedy.
Aplikace konkrétního pravidla na nějaký řetězec pak vypadá následovně:
- Najde se první (nejlevější) výskyt vzoru v řetězci.
- Tento výskyt se vymaže a na jeho místo se vloží přepis.
Pravá strana (přepis) může být i prázdná. Takové pravidlo lze například využít
k vymazání části vstupu. Vzor naopak prázdný být nemůže, vždy musí obsahovat
alespoň jeden znak nebo metaznak.
Uvažme například následující pravidla:
Každé samostatně aplikujeme na vstup baa. První pravidlo ho přepíše
na bba, druhé na bab a třetí pravidlo nic nepřepíše (takovýto
vzor ve vstupu neexistuje, a tedy se nic neprovede).
Samostatnou aplikací pravidel ovšem dost silný výpočetní model nedostaneme.
Na to bude potřeba poskládat více pravidel dohromady.
Přepisovací programy
Přepisovacím programem nazveme nějaký uspořádaný soubor přepisovacích
pravidel, čili několik pravidel seřazených za sebe.
Výpočet přepisovacího programu probíhá v krocích: první krok přepisuje
vstup programu, výstup prvního kroku se stane vstupem druhého, a tak stále
dokola. Výpočet končí ve chvíli, kdy již mezi pravidly neexistuje žádné,
jehož vzor by se vyskytoval ve vstupu. To se samozřejmě nemusí stát – jistě
snadno vymyslíte přepisovací program, který se nikdy nezastaví. (Jednou
z možností je třeba program skládající se z jediného pravidla $
→a. Ten nikdy neskončí, protože vzor pravidla je obsažen
v každém řetězci.)
Výpočet každého kroku by se dal formálně popsat takto:
- Najde se první pravidlo, jehož vzor se vyskytuje někde ve vstupu.
- Toto pravidlo se provede (najde se první výskyt vzoru ve vstupu a na jeho
místo se vloží přepis).
- Výstup tohoto pravidla se použije jako vstup dalšího kroku. Výpočet dalšího
kroku začíná opět od prvního pravidla a od začátku řetězce.
Zbývá zavést nějakou míru efektivity – analogii časové složitosti
normálních programů. Nám pro tyto účely bude sloužit počet provedených kroků
přepisovacího programu. (Na zamyšlení: co by odpovídalo prostorové
složitosti?)
Příklady
Pojďme vyzkoušet, co přepisovací programy dovedou.
První příklad bude jednoduchý. Představte si, že máme zadanou posloupnost
nul a jedniček (třeba 01101) a chceme ji setřídit. Jinými slovy chceme
přesunout všechny nuly nalevo od jedniček.
To půjde překvapivě snadno. Sestrojíme program obsahující jediné pravidlo:
10 →01
Na našem ukázkovém vstupu bude výpočet probíhat takto:
01101,
01011,
00111.
Povšimněme si, že dokud posloupnost není setříděná, existuje v ní aspoň
jedna po sobě jdoucí dvojice 10, takže program běží dál.
Doběhne někdy? Sledujme inverze v posloupnosti: tak budeme
říkat dvojicím (ne nutně sousedních) čísel, která jsou ve špatném pořadí.
Naše ukázková posloupnost obsahuje 2 takové dvojice. Každé použití pravidla
sníží počet inverzí právě o jedna, takže se program po konečně mnoha krocích
musí zastavit.
Jak dlouho náš program poběží? Ve vstupu délky n může být nejvýše (n/2)2
inverzí (to odpovídá situaci, kdy na vstupu máme n/2 jedniček a za nimi n/2 nul)
a program je odstraňuje po jedné, takže provede řádově n2 kroků. (Mimochodem, pokud
budeme provádět chytřejší operace než pouhé prohazování, je možné dosáhnout
i lepší efektivity. Zkuste vymyslet, jak.)
Druhý příklad už bude záludnější. Možná si vzpomínáte na kontrolu
správnosti uzávorkování z minulé série. Pojďme si ukázat, jak snadno se dá
vyřešit pomocí přepisovacích pravidel.
Na vstupu budeme mít posloupnost levých a pravých závorek a naším úkolem bude
rozhodnout, jestli tvoří správné uzávorkování, nebo netvoří. Podle toho vrátíme
na výstupu buď ANO, nebo NE. Pro připomenutí, správné uzávorkování je
takové, ve kterém jsou závorky správně spárované a páry se nekříží.
Idea našeho přepisovacího programu bude takováto: Všimneme si, že se v každé
neprázdné správně uzávorkované posloupnosti vyskytuje po sobě jdoucí dvojice ().
Tu můžeme odstranit, čímž získáme další správně uzávorkovanou posloupnost, a tak dále,
až nakonec dospějeme k prázdné posloupnosti. Funguje to i naopak: přidáním ()
do jakéhokoliv správného uzávorkování nelze získat nesprávné, takže se nemůže
stát, že bychom na prázdný řetězec zredukovali nějaké nesprávné uzávorkování.
Program vypadá následovně:
X$ | →NE |
X( | →X |
X) | →X |
() | → |
^$ | →ANO |
^( | →X |
^) | →X |
Dokud vše probíhá tak, jak má, čtvrté pravidlo umazává závorky. Pokud umaže
všechny závorky, páté pravidlo vypíše ANO. Pokud ale již nebude možné
umazat žádnou dvojici závorek, nastoupí jedno z posledních dvou pravidel a na
scénu přijde X. To pak za pomoci prvních tří pravidel vymaže zbytek
vstupu, vypíše NE a program se zastaví.
Rozmyslete si, proč namísto posledních dvou pravidel nemůžeme použít
^ → X. (Správná odpověď je, že pak by se nám
program nikdy nezastavil, protože vzor takového pravidla by byl nalezen vždy.)
Úlohy
Vymyslete přepisovací programy na následující problémy. U všech programů
odhadněte efektivitu (v počtu provedených kroků) a pokuste se o co nejlepší.
Součástí řešení by měl být slovní popis a alespoň náznak zápisu použitých
přepisovacích pravidel.
Úkol 1 [2b]
Vstup je tvořený posloupností čísel 0 až 9. Vaším úkolem je zanechat
na výstupu ANO, pokud je posloupnost čísel neklesající, a NE
v opačném případě.
Úkol 2 [3b]
Na vstupu je posloupnost znaků *. Spočítejte, kolik jich je, a výsledek
zanechte na výstupu jako číslo ve dvojkové soustavě.
Úkol 3 [5b]
Na vstupu jsou dvě čísla ve dvojkové soustavě oddělená křížkem #.
Na výstupu nechť se objeví to větší z nich. Pozor, zápisy čísel nemusí být
stejně dlouhé. Případ, kdy jsou si čísla rovna, nemusíte uvažovat.
Převod na Turingův stroj a naopak
Jak už jsme zmínili v úvodu, přepisovací pravidla a Turingovy stroje spolu úzce
souvisí. Ukážeme, jak převést jakýkoli přepisovací program na Turingův stroj.
Nejdříve se zamyslíme, jak převést jedno přepisovací pravidlo do řeči Turingova
stroje. Začneme s hlavou na levém konci pásky a budeme se postupně pokoušet
najít výskyt vzoru (vyzkoušíme všechny začátky a vždy porovnáme se vzorem;
stav stroje bude říkat, kolikátý znak vzoru porovnaváme).
Ve chvíli, kdy nalezneme první výskyt, přepneme se do dalšího stavu a pásku
přepíšeme odpovídajícím přepisem (a případně odsuneme či přisuneme zbytek znaků
na pásce, pokud přepis bude mít jinou délku než vzor). A nakonec, po dokončení
přepisování, vrátíme hlavu opět na začátek pásky (a stejně tak v případě, že se
nám nepovede najít žádný výskyt vzoru).
Tím jsme úspěšně naučili Turingův stroj zpracovat jedno pravidlo. K překladu
celého přepisovacího programu už zbývá jen krůček. Každé pravidlo v programu
bude mít svou vlastní sadu stavů (sady nechť jsou třeba očíslované). Po úspěšném
provedení pravidla a návratu hlavy zpět na začátek pásky se přesuneme do
první sady; po neúspěšném hledání vzoru se přesuneme do následující sady
(zkusíme aplikovat další pravidlo v pořadí). Pokud budeme neúspěšní i
u posledního pravidla, ukončíme výpočet.
Právě jsme dokázali, že každý přepisovací program lze simulovat Turingovým
strojem. Pokud navíc ukážeme, že každý Turingův stroj lze převést na přepisovací
program, bude jasné, že oba výpočetní modely jsou stejně silné (co jde
spočítat v jednom, jde i ve druhém a opačně). To už ale bude na vás:
Úkol 4 [4b]
Dokažte, že pro každý jednopáskový Turingův stroj existuje přepisovací program,
který počítá totéž. Přesněji řečeno, pokud se pro daný vstup Turingův stroj
zastaví, přepisování se také zastaví a vydá stejný výsledek. Pokud se stroj
nezastaví, přepisování se také nezastaví. Rozmyslete si, v jakém vztahu je
časová složitost stroje a pravidel. Svůj přístup demonstrujte na stroji
z příkladu v 1. sérii (vyvážená posloupnost).
Jirka Setnička & Martin „Medvěd“ Mareš
Řešení
