Druhá série dvacátého šestého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

26-2-1 Zamotané provazy (Zadání)

Prvním postřehem může být, že počet křížení musí být vždy sudý, jinak nemůže být provaz 2 nahoře na obou stromech. Dále si lze všimnout, že když je na dvou po sobě jdoucích kříženích nahoře stejný provaz, jde jen o přehozenou „vlnu“, a lze ji bez problémů rozmotat.

Pokud budeme postupně odstraňovat dvojice stejných křížení, dobereme se k jednomu ze dvou stavů. Pokud nám zbyly dva provazy bez křížení, jde je rozmotat. Jinak budou tvořit posloupnost, ve které se pouze střídají jedničky a dvojky, a kterou již rozmotat nelze.

Velmi se nabízí možnost implementovat program pomocí zásobníku. Každé nové překřížení porovnáme s vrcholem zásobníku a pokud se liší, přidáme nové křížení. Pokud jsou stejné, vrchol odebereme. Takto se určitě dostaneme ke každé dvojici, kterou bychom odebrat mohli. Už teď máme algoritmus lineární s počtem křížení a toto stačilo na zisk 6 bodů.

Lépe než lineárně to samozřejmě nepůjde, každé křížení ovlivňuje výsledek. Pomůžeme si ale s pamětí a to vynecháním zásobníku. Můžeme si to dovolit, protože se v něm po sobě jdoucí prvky vždy liší – jde vždy o střídající se jedničky a dvojky. Stačí si tedy pamatovat, čím zásobník končí a jak je hluboký.

Optimálním řešením je tedy výše popsaný algoritmus běžící v čase O(N) a využívající O(1) paměti. Za takové řešení jsme už dávali plný počet bodů.

Program (C)

Ondra Hlavatý & Jirka Setnička

26-2-2 Barevný trojúhelník (Zadání)

V řešení se inspirujeme myšlenkou, kterou nám zaslal řešitel Matej Lieskovský. Předpokládejme pro spor, že v síti neexistuje souvislá oblast spojující všechny tři strany. Vezměme horní vrchol trojúhelníka a uvažme největší jednobarevnou souvislou oblast, ve které leží.

Tato oblast, řekněme bez újmy na obecnosti bílá, se dotýká minimálně dvou stěn, kterých se dotýká vrchol. Z předpokladu se však nedotýká třetí. Je tedy zespoda zcela ohraničena souvislým pásem černých šestiúhelníků, který navíc spojuje ty samé dvě stěny, které spojuje zvolená bílá oblast. To opět z předpokladu znamená, že tato černá oblast nezasahuje do třetí strany.

Nahlédněme, že když celou bílou oblast u horního vrcholu přebarvíme na černo, nevznikne tím souvislá oblast spojující tři strany – tato oblast spojuje stejné dvě strany jako její černá hranice, takže spojení se třetí stranou nevznikne. Tím jsme ovšem zvýšili aspoň o 1 počet černých šestiúhelníků a dostali jsme opět obrazec bez souvislé oblasti spojující všechny 3 strany.

Tuto operaci můžeme opakovat kolikrát chceme, ovšem po určitém počtu kroků musíme dojít do stavu, kdy už bude černý celý trojúhelník. To je ovšem obrazec, ve kterém už zřejmě existuje souvislá jednobarevná oblast spojující všechny tři strany, což je hledaný spor. Tím je důkaz hotov.

Alternativní interpretace stejné myšlenky by fungovala následovně: Pomocí pozorování výše snadno ukážeme, že v daném obarvení existuje souvislá oblast spojující všechny tři strany právě tehdy, když existuje taková oblast v obarvení, kde přebarvíme onu souvislou oblast při některém vrcholu.

Když tedy budeme dostatečně dlouho takto přebarvovat, opět dostaneme zcela černý trojúhelník, který už takovou všespojující oblast obsahuje. Z tohoto stavu ovšem můžeme do stavu, kde jsme začali, natáhnout řetěz výše popsaných ekvivalencí, takže existuje-li ve finálním stavu oblast spojující všechny tři strany, existuje i v původním obrazci.

Mark Karpilovskij

26-2-3 Plánování cesty (Zadání)

Úloha o plánování Jacobovy cesty nebyla ničím jiným, než hledáním nejkratší cesty v grafu. Přeformulujme si úlohu nejprve z řeči čtvercových políček do čisté řeči grafů.

Definujme orientovaný ohodnocený graf G. Vrcholy grafu budou políčka zadané oblasti. Hrany mezi dvěma políčky vedou právě tehdy, když spolu obě políčka sousedí stranou a obě jsou průchozí. Ohodnocení hrany z políčka A do políčka B bude odpovídat času potřebnému na zdolání políčka B.

Průchod do šířky

Graf G má RS vrcholů a O(RS) hran, kde R×S jsou rozměry oblasti. Řešením původní úlohy je délka nejkratší cesty v G ze startovního políčka do cílového políčka.

Prvním způsobem, jak úlohu řešit, je prohledat graf do šířky. Prohledávání do šířky (BFS) je popsáno v naší grafové kuchařce a zde jej nebudeme opakovat.

Nesmíme ovšem zapomenout, že prohledávání do šířky funguje pouze v případech, kdy ohodnocení všech hran je jednotkové. Nejprve musíme ještě provést jednu úpravu grafu. Využijeme celočíselnosti ohodnocení hran a každou hranu nahradíme posloupností jednotkových hran. Konkrétně hranu s ohodnocením t nahradíme cestičkou složenou z t jednotkových hran. Takové operaci se také říká podrozdělení.

Pokud označíme jako T nejvyšší z ohodnocení všech hran, můžeme počet hran i vrcholů nového grafu omezit výrazem O(TRS). Nejkratší cesta v podrozděleném grafu odpovídá nejkratší cestě v původním grafu.

Na tomto grafu už použijeme prohledávání do šířky a získáme řešení s časovou složitostí O(TRS).

Dodejme ještě, že si můžeme vystačit s prostorem velikosti O(RS). Nově přidané vrcholy a hrany si totiž nemusíme nutně pamatovat. Stačí pracovat s původním G a akorát při vkládání vrcholu do fronty přidělit vrcholu jakési „zpoždění“, se kterým má být zpracován. Zpoždění nejprve nastavíme na ohodnocení hrany. Po vyjmutí vrcholu z fronty zpoždění snížíme o jedna. Je-li zpoždění stále větší než nula, vrchol nezpracujeme, ale znovu jej vložíme do fronty.

Dijkstrův algoritmus

S pomocí průchodu do šířky bylo možno zdárně vyřešit prvních pět vstupů, v dalších pěti testovacích vstupech již byla hodnota T příliš vysoká a bylo nutno využít sofistikovanější algoritmus.

Mezi takové algoritmy se například řadí Dijkstrův algoritmus, který je vlastně rozvinutím předchozí myšlenky o zpožděných vrcholech. Dijkstrův algoritmus je důkladně vyložen v další z našich kuchařek. Kuchařka shodou okolností vychází letos zároveň se zadáním třetí série a bylo by zbytečné zde její obsah opakovat.

Použijeme-li při implementaci Dijkstrova algoritmu binární haldu, dosáhneme časové složitosti O((N+M) log N), kde N je počet vrcholů a M počet hran grafu. V našem případě získáváme řešení s časovou složitostí O(RS log RS). Paměťová složitost řešení bude O(RS).

Můžete si povšimnout, že použití k-regulární či Fibonacciho haldy by nám v našem konkrétním problému nepomohlo. Graf je totiž velmi řídký (má pouze lineární počet hran vzhledem k počtu vrcholů).

Program (C) – průchod do šířky

Program (C) – Dijkstrův algoritmus

Lukáš Folwarczný

26-2-4 Stavba věže (Zadání)

Lehčí varianta

Jakmile víme, že všech K kostek má stejnou váhu, můžeme si je setřídit podle jejich nosnosti. Poté je budeme postupně procházet od největší k nejmenší a budeme kontrolovat, že nosnost ℓi ≥ K-i-1 (kde i je index v poli, které je číslováno od nuly).

Proč to můžeme udělat právě takto? Protože potřebujeme, aby každá kostka unesla všechny nad sebou. Ty váží právě K-i-1 (pokud mají všechny jednotkovou váhu) a pokud bude tato nerovnost splněna pro každou kostku, tak takovou věž určitě postavit můžeme.

Pokud by naopak tato nerovnost na nějakém místě splněna nebyla, tak bychom aktuální kostku mohli prohodit jenom za nějakou kostku výše (protože kdybychom ji prohodili níž, musela by unést ještě víc). Jenže všechny kostky nad aktuální mají nosnost menší nebo rovnou aktuální, takže v takovém případě neexistuje způsob, jak by věž šla postavit.

Časová složitost takového řešení je O(K log K), protože právě tak dlouho budeme třídit. Kontrola, že lze věž postavit, už proběhne jen v čase O(K). Taková řešení jsme ohodnotili slíbenými 3 body, tedy maximem za lehčí variantu.

Ale lehčí variantu lze vyřešit i v čase O(K). Uděláme to takto:

  1. Vytvoříme pole o velikosti K (opět číslujeme od nuly).
  2. Projdeme kostky a u těch, které mají ℓi ≥ K, nastavíme jejich nosnost na K-1 (protože větší nosnost nepotřebujeme, stačí nám, aby unesly maximálně K-1 kostek).
  3. Postupně projdeme všechny kostky a do pole velikosti K si zapíšeme, kolik kostek má kterou nosnost (tedy budeme indexovat pole přímo nosností).
  4. Poté si vybereme jednu kostku s nosností K-1. Pokud taková neexistuje, je jasné že věž postavit nelze a zahlásíme neúspěch. Pokud existuje, tak ji smažeme a spustíme náš algoritmus znovu pro K o jedna menší.

Ale počkat, to bude přece trvat až O(K2)! Zkusíme tedy vzít jenom hlavní myšlenku a vylepšíme ji. Rozmysleme si, jak se nám pole po smazaní jedné kostky ve 4. bodě změní.

Kostky, které měly předtím nosnost ℓi < K-1, to nijak neovlivní, ty zůstanou na stejném místě. Jediné, co se změní, jsou kostky s nosností ℓi ≥ K-1, tyto (až na tu jednu smazanou) dostanou nosnost ℓi = K-2.

Z toho nám vyplývá, jak naprogramovat řešení. První tři kroky uděláme přesně tak, jak je napsáno výše, ale 4. krok uděláme trochu chytřeji – uvědomíme si, že vlastně vůbec není nutné celé pole počítat pokaždé znova.

Stačí nám jednu kostku o nosnosti K-1 odečíst a všechny kostky o stejné nosnosti, které nám zbyly, přičíst ke kostkám s nosností K-2. Takto upravený 4. krok budeme opakovat, dokud se nedostaneme na K = 0. Pokud jsme cestou nenarazili na žádné potíže, tak lze celá věž postavit.

Těžší varianta

V případě, že mají kostky rozdílné váhy, nám už nebude stačit obyčejné třídění podle nosnosti. Jako protipříklad použijeme dvě kostky: w1 = 1,  ℓ1 = 3 a w2 = 4,  ℓ2 = 2. Podle nosností bychom chtěli nejdříve umístit první, která už druhou neunese. Prohlásili bychom tedy, že věž nelze postavit. Druhá kostka však první unese, ale my bychom tuto možnost ani nevyzkoušeli.

Jak tedy úlohu vyřešit? Mnozí z vás správný postup vymysleli. Obtížnější však bylo dokázat, že řešení opravdu funguje. Ukážeme si kromě algoritmu a důkazu i to, jak můžeme na takové řešení přijít postupně.

Věž stavíme odspoda v jednotlivých krocích. Na začátku máme věž nulové výšky a hromádku všech kostek. V každém kroku z hromádky vybereme ty kostky, které unesou všechny zbývající kostky na hromádce. Vybrané kostky můžeme přidat v libovolném pořadí do věže.

Pokud se nám podaří tímto způsobem věž postavit ze všech kostek, tak máme vyhráno, protože jsme nikdy nepoužili takovou kostku, která by neunesla vše nad sebou. Pokud věž nesestavíme, tak jsme nalezli hromádku, ze které ani jedna kostka neunese všechny zbývající. Z této hromádky však nelze nikdy postavit věž – žádná kostka nemůže být základnou věže. Přidáním dalších kostek si celou konstrukci můžeme zatížit, nikdy ji však neodlehčíme. Věž tedy nejde postavit ani ze všech kostek.

Okamžitě tak dostáváme algoritmus, který úlohu řeší v čase O(K3). Provedeme totiž nejvýše K kroků, kde v každém z nich spočítáme pro každou kostku součet hmotností všech zbývajících.

Nyní si můžeme všimnout, že při sčítání hmotností ostatních kostek sčítáme dokola téměř ta samá čísla. Lepší tedy bude si předem spočítat součet hmotností všech kostek na hromádce, označme jej třeba S. Do věže potom můžeme přidat kostky, pro které platí S - wi ≤ ℓi, tedy ekvivalentně S ≤ ℓi + wi.

Když se nyní podíváme na vývoj S po jednotlivých krocích, zjistíme, že se číslo S pouze snižuje. Nic nám tedy nebrání kostky vybírat v pořadí od největší po nejmenší podle součtu wi + ℓi.

Algoritmus díky tomu můžeme velmi zjednodušit a urychlit. Kostky nejprve setřídíme podle součtu hmotnosti a nosnosti. A následně v lineárním čase ověříme, zda se kostky unesou. K tomu stačí, když půjdeme od špičky věže dolů a vždy porovnáme nosnost aktuální kostky se součtem hmotností kostek nad ní. Tento součet si v průběhu snadno spočítáme z předchozího pouhým přičtením hmotnosti další kostky. Celý algoritmus tak doběhne v čase O(K log K) a spotřebuje při tom O(K) paměti.

Program (C) – lehčí varianta

Program (C++) – těžší varianta

Vojta Sejkora & Jenda Hadrava

26-2-5 Vyvažování (Zadání)

Vyhledávací stromy lze vyvažovat mnoha různými algoritmy, které všechny pracují v lineárním čase, ovšem liší se množstvím potřebné paměti. Začneme tím nejobyčejnějším, který potřebuje lineární pracovní prostor, a postupně se propracujeme až ke konstantní paměti.

Rozebrat a složit: lineární prostor

Přetvářet nevyvážený strom na vyvážený pomocí lokálních úprav vypadá složitě. Co kdybychom ho prostě rozebrali a pak znovu poskládali?

Rozebírání proběhne rekurzivním průchodem stromu: vždy projdeme nejprve levý podstrom, pak kořen a nakonec pravý podstrom. Takto jednotlivé vrcholy navštívíme ve vzestupném pořadí. Stačí si je tedy průběžně ukládat do pole.

Ze setříděného pole posléze vyrobíme dokonale vyvážený strom: kořenem bude prvek, který v poli leží uprostřed (tedy medián). Hodnoty ležící v poli před ním patří do levého podstromu, hodnoty za ním do pravého. Oba podstromy sestrojíme rekurzivně a zavěsíme pod kořen. Do rekurze přitom stačí předávat počáteční a koncový index úseku pole, ze kterého zrovna stavíme strom.

Jak rozebrání starého stromu, tak postavení nového nás stojí O(n), kde n je počet vrcholů stromu. Na co všechno spotřebujeme paměť? Předně si musíme uložit lineárně velké pole hodnot. Nesmíme také zapomenout na zásobník od rekurze: na něm bude najednou tolik položek, kolik činí hloubka stromu. Ta může při rozebírání dosáhnout až n, během skládání pak pouze O(log n). Prostoru tedy celkem zabereme O(n).

Rozebrání stromu na seznam

Pojďme se zbavit zbytečné kopie hodnot. Místo kopírování vrcholy zadaného stromu popřepojujeme, aby tvořily liánu, tedy strom, v němž nejsou žádní leví synové. Ukazatele na pravé syny nám tedy tvoří obyčejný spojový seznam, navíc setříděný podle hodnot.

K převodu stromu na liánu se budou hodit rotace (viz kuchařka). Ty umožňují měnit tvar stromu, a přitom stále zachovávají uspořádání vrcholů (strom je tedy stále vyhledávací).

Budeme postupovat takto: dokud má kořen levého syna, provádíme v kořeni rotaci doprava. Když už levého syna nemá, sestoupíme do jeho pravého syna a tam algoritmus opakujeme.

Ukažme si, jak to vypadá pro jeden strom se 7 vrcholy (tučně je vždy vyznačena hrana, kterou se chystáme rotovat):

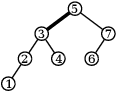
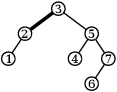
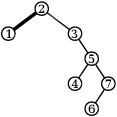
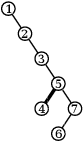
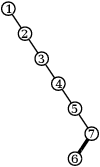
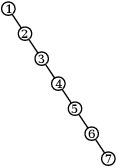
Rozebrání stromu na seznamRozebrání stromu na seznamRozebrání stromu na seznam
Rozebrání stromu na seznamRozebrání stromu na seznamRozebrání stromu na seznam

Proč to funguje? Stačí si všimnout, že mezi kořenem a aktuálním vrcholem leží nějaká už sestrojená liána. Rotace ji nepokazí a po konečně mnoha rotacích (každá zmenšuje velikost levého podstromu) učiníme jeden krok doprava, který liánu prodlouží. Algoritmus se tedy musí zastavit a v tu chvíli je celý strom liánou.

Kolik celkem strávíme času? Kroků doprava je lineárně. Abychom ukázali, že rotací také, stačí sledovat, jak se vyvíjí délka pravé cesty. To je cesta vedoucí z kořene doprava, dokud to jde. Každá rotace ji prodlouží o 1, ovšem délka cesty nikdy nepřekročí n, takže všech rotací je nejvýše n.

Logaritmické řešení

Nyní upravíme funkci na převod seznamu na strom, aby si vystačila se seznamem namísto pole.

Problematické místo je hledání prostředního prvku: v poli byl přístupný v konstantním čase, v seznamu bychom ho hledali lineárně dlouho, čímž bychom si pokazili celkovou časovou složitost.

Místo toho rekurzivní funkci navrhneme tak, aby dostala jako parametry seznam S a počet prvků k. Funkce odpojí prvních k prvků seznamu, vytvoří z nich strom T a vrátí jak tento strom, tak zbytek seznamu S''.

V pseudokódu bychom ji zapsali třeba takto:

Strom(S,k):
  1. Je-li k=0, vrátíme prázdný strom a seznam S.
  2. ℓ←⌊(k-1)/2 ⌋
  3. (L,S') ←Strom(S,ℓ)
  4. x ←odpojíme první prvek seznamu S'
  5. (P,S'') ←Strom(S',k-ℓ-1)
  6. Vytvoříme strom T: kořen bude mít hodnotu x, jeho levým podstromem bude L a pravým P.
  7. Výstup: Dvojice (T,S'').

Čas je opět lineární, paměti nám stačí O(log n) na zásobník.

Konstantní prostor pro úplné stromy

Ani logaritmický prostor ovšem není nutný. Ukážeme řešení v konstantním prostoru, zatím ovšem pouze pro úplné stromy. Tak budeme říkat stromům, v nichž mají všechny vnitřní vrcholy právě 2 syny a všechny listy leží na téže hladině. Úplný strom hloubky h má tedy

20 + 21 + … + 2h = 2h+1 - 1

vrcholů. (Jiná možnost, jak úplné stromy definovat, je ještě zesílit definici dokonalé vyváženosti a požadovat, aby levý a pravý podstrom byly pokaždé přesně stejně velké. Proto se jim také někdy říká perfektní stromy.)

Dostaneme tedy seznam délky mocnina dvojky minus 1 a máme z něj vyrobit úplný strom.

Algoritmus bude jednoduchý, ale nečekaný. Jeho průběh sledujme na obrázcích níže (tučně je opět zvýrazněna hrana, kterou rotujeme; vlasové čáry pod vrcholy zatím ignorujte).

Půjdeme z kořene doprava a v každém kroku provedeme jednu rotaci doleva. Tím nám z cesty vznikne „hřeben“ – pravá cesta poloviční délky, z jejichž vrcholů vedou levé odbočky do listů.

Poté průchod z kořene doprava zopakujeme. Pravá cesta se opět dvakrát zkrátí a na levých odbočkách budou už viset „třešničky“ – úplné stromy hloubky 1 se třemi vrcholy. Další průchod vytvoří úplné stromy hloubky 2 se sedmi vrcholy a tak dále.

Nakonec celou pravou cestu rozebereme a zbude nám jeden úplný strom.

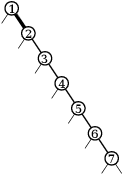
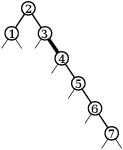
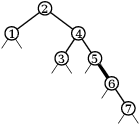
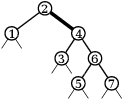
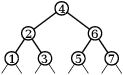
Rozebrání stromu pomocí rotacíRozebrání stromu pomocí rotacíRozebrání stromu pomocí rotací
Rozebrání stromu pomocí rotacíRozebrání stromu pomocí rotací

Času jsme spotřebovali lineárně: hran na pravé cestě je na počátku n-1 a každá rotace jednu odstraní. Prostor potřebujeme pouze na konstantně mnoho pracovních proměnných.

Konstantní prostor pro všechny stromy

Dobrá, ale co když počet vrcholů není tak hezké číslo, aby šlo sestrojit úplný strom? Tehdy najdeme nejbližší menší číslo m tvaru 2i-1, z tolika prvků seznamu sestrojíme úplný strom a zbylých r=n-m vrcholů pověsíme pod listy úplného stromu.

Zařídí se to snadno: pokud k některým vrcholům počáteční liány přivěsíme levé syny a spustíme algoritmus pro úplné stromy, tak se tyto „přívěsky“ objeví právě pod listy úplného stromu. (To znázorňují ony vlasové čáry v obrázku, které jsme napoprvé přehlíželi.)

Náš obecnější algoritmus tedy projde liánu a celkem r-krát provede rotaci doleva, aby se z části vrcholů staly přívěsky a zbyla pravá cesta délky m, na kterou půjde spustit původní algoritmus.

Oněch r rotací se samozřejmě budeme snažit rozmístit co nejrovnoměrněji. Uděláme to takto: pořídíme si proměnnou, která bude na počátku nulová, v každém kroku k ní přičteme r/m a kdykoliv překročí 1, tak zrotujeme a odečteme 1.

Dokonce se můžeme zbavit dělení: místo původní proměnné si budeme pamatovat její m-násobek. Začneme tedy na nule, pokaždé přičteme r a pokud překročíme m, zrotujeme a odečteme m. (Mimochodem, přesně tento postup se používá při aproximování úseček pomocí pixelů na obrazovce.)

Zbývá dokázat, že skutečně vyjde dokonale vyvážený strom. Pro každý vrchol má platit, že rozdíl velikostí levého a pravého podstromu činí nejvýše 1. Jelikož v úplném stromu jsou oba podstromy stejně velké, stačí ukázat, že se počty přívěsků pod nimi liší nejvýše o 1.

Všimneme si, že vrcholy obou podstromů tvoří v liáně souvislé úseky, navíc stejně dlouhé. Ukážeme, že pro každé dva úseky stejné délky platí, že se počty přívěsků pod nimi liší nejvýše o 1.

Počítejme, kolik náš algoritmus mohl vygenerovat přívěsků pro úsek délky u. Nechť pomocná proměnná řídící přivěšování má na začátku úseku hodnotu h (víme, že 0 ≤ h < m). Pak vytvoříme celkem ⌊(h+ur)/m⌋ přívěsků. Tento výraz je nejmenší pro h=0 a největší pro h=m-1, přičemž obě krajní hodnoty se mohou lišit nejvýše o 1. (Neboť pro každé x platí ⌊x+1⌋ = ⌊x⌋+1.)

Výsledný strom je tedy dokonale vyvážený a na jeho vytvoření nám postačil lineární čas a konstantní paměť.

Program (C) – řešení pomocí rotací

Uvedený algoritmus pochází z článku Tree Rebalancing in Optimal Time and Space od Quentina F. Stouta a Bette L. Warrenové, na který nás upozornili řešitelé. Aneta Šťastná navíc navrhla jednodušší rozmisťování přívěsků, kterým jsme se také inspirovali.

Alternativní řešení

Když jsme úlohu zadávali, měli jsme vymyšlený úplně jiný způsob řešení. Jeho rozbor se všemi detaily je trochu pracnější, základní myšlenka ovšem také stojí za zmínku.

Upravíme logaritmické řešení, aby nepotřebovalo tolik paměti na zásobník. Budeme předpokládat, že každý vrchol si kromě ukazatelů na syny pamatuje i ukazatel na otce (časem se ukáže, že to není potřeba).

Představme si nejprve, jak libovolný strom projít ve vzestupném pořadí hodnot bez použití rekurze. Začneme v kořeni a řídíme se následujícími pravidly:

Při konstrukci stromu si budeme počínat obdobně: vytvářený strom budeme takto „obcházet“ a místo abychom vrcholy vypisovali, tak je budeme zakládat.

To se snadno řekne, ale při implementaci nás čeká několik překážek.

Předně potřebujeme udržovat plánovanou velikost podstromu (proměnná k v logaritmickém řešení). Při kroku dolů ji prostě dělíme dvěma, leč při kroku nahoru nestačí násobit dvěma, neboť původní hodnota mohla být lichá. To vyřešíme tak, že si v každé úrovni rekurze zapamatujeme zbytek po dělení dvěma. To je jeden bit na každé z O(log n) úrovní, takže se všechny dají poskládat do jediného čísla velkého řádově n.

Další potíž je, že občas potřebujeme přejít přes vrchol, který jsme ještě nevytvořili. To není těžké, ale při programování to řádně zamotá hlavu. Postačí, když budeme udržovat nejbližší vyšší vrchol, který skutečně existuje, a aktuální hloubku.

Co víc, k neexistujícímu vrcholu také občas potřebujeme něco připojit. Tak to připojíme k onomu nejbližšímu vyššímu existujícímu a navíc si zapamatujeme, ze které strany připojujeme (to je opět bit na úroveň).

Konečně si potřebujeme pro každou úroveň pamatovat, jestli aktuální vrchol na této úrovni ještě není vytvořen (tzn. zrovna jsme zalezlí kdesi v jeho levém podstromu), nebo už existuje (levý podstrom hotov, teď jsme někde v pravém).

Tímto způsobem také dosáhneme lineárního času a konstantní paměti.

Program (C) – alternativní řešení

Dva pointery místo tří

Na závěr jedna pozoruhodná perlička: způsob uložení binárního stromu se dvěma pointery na vrchol, který umožňuje v konstantním čase zjistit levého syna, pravého syna i otce libovolného vrcholu.

První pointer (říkejme mu třeba P) bude ukazovat na levého syna. Druhý (řečený Q) bude v levém synovi ukazovat na jeho pravého sourozence, ale v pravém synovi na otce.

Levého syna vrcholu tedy zjistíme pomocí P. Pravého pomocí Q z levého syna. Pokud chceme znát otce, zkusíme přejít pomocí Q a podíváme se, zda jsme se dostali do vrcholu s menší hodnotou. Pokud ano, je to hledaný otec. Pokud ne, dostali jsme se do pravého sourozence, takže přejdeme ještě jednou po Q.

Pokud by vrchol měl jen jediného syna, bude na něj ukazovat P a jeho Q se odkáže zpět na otce. Porovnáním hodnot zjistíme, zda je to levý či pravý syn.

Martin „Medvěd“ Mareš & Dominik Macháček

26-2-6 Zkratky míst (Zadání)

Všimněme si, že slova s různým počátečním písmenem nikdy nemůžou mít stejnou zkratku. Zkratka je totiž určená prvním písmenem slova a pak nějakým výběrem dalších dvou písmen z něj.

Můžeme tedy úlohu řešit samostatně pro každé počáteční písmeno a úloha se nám tak pro jednu „hromádku“ se stejným počátečním písmenem zjednodušuje na nalezení unikátních dvoupísmenných zkratek sestávajících se ze zbylých písmen slova (mimo prvního) ve správném pořadí.

Pokud jste již někdy slyšeli o problému hledání maximálního párování v bipartitním grafu, určitě vám jej tato úloha trochu připomíná. Pokud ne, doporučujeme vaší pozornosti příslušný článek v naší zbrusu nové programátorské encyklopedii.

Jednu partitu (říkejme jí levá) tvoří slova, druhou (pravou) všechny možné zkratky. Hrany vedou z každého slova do všech zkratek, které z něj lze utvořit. Pak párování v tomto grafu odpovídá nějakému přiřazení zkratek slovům. Nyní stačí prostě najít párování maximální, tedy takové, které co nejvíce slovům přiřadí zkratku. Pro množinu slov {ara, arab, bar} by mohl graf vypadat takto:

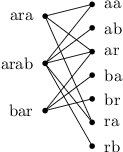
Mohlo by vás ještě trochu překvapit, že si na úlohu bereme takto obecné kladivo. Naše zkratkové grafy přece mají velice speciální tvar, fakt, kterého obecný párovací algoritmus nijak nevyužije. To se občas hodí, když se náš problém podobá nějakému známému, na chvíli se tvářit, že jsou stejné. Nebojte, za chvíli se k alespoň některým zvláštnostem zkratkového grafu zase vrátíme.

Označme si N počet vstupních slov, S součet jejich délek a |Σ| velikost abecedy. Než se pustíme do rozboru složitosti, ještě přidáme do algoritmu malý zlepšovák: při načítání vstupu upravíme slova tak, že v každém zachováme pouze první a poslední výskyt libovolného písmene. Snadno si rozmyslíte, že tím nijak nezměníme množinu zkratek, které lze ze slova vytvořit. V každém takto upraveném slově se libovolné písmeno abecedy vyskytuje nejvýše dvakrát, je tedy dlouhé O(|Σ|), a tudíž S = O(N · |Σ|).

Jak bude náš graf velký? Možných zkratek existuje |Σ|2, počet vrcholů tedy bude N + |Σ|2. V nejhorším případě, kdy každé slovo obsahuje všechna písmena abecedy a půjde z něj vytvořit řádově |Σ|2 zkratek, bude graf obsahovat N|Σ|2 hran.

Pokud je abeceda malá, můžeme |Σ| prohlásit za konstantu a dostaneme příjemný lineárně velký graf. Graf sestavíme v čase O(N · |Σ|2) (díky tomu, že každé slovo je nyní dlouhé O(|Σ|)), tedy pro malou abecedu O(N).

Budeme-li, jako v odkazovaném článku, párovat postupným hledáním zlepšujících cest, které běží v čase O(|M| · |E|) (kde |E| je počet hran grafu a |M| velikost výsledného párování), potrvá to O(N2). Paměti spotřebujeme O(N) na uložení grafu.

Kdož jste zvyklí převádět párování na toky v sítích, vězte, že nejde o nic jiného než jinou formulaci Ford-Fulkersonova algoritmu pro párovací sítě. My zde používáme tuto verzi, protože další úpravy a optimalizace se na ní budou popisovat snáz než v tokové formulaci.

Program (Python)

Toto řešení je dostačující jak pro většinu běžných použití (anglická abeceda, ASCII), tak pro získání plného počtu bodů. Prostou výměnou párovacího algoritmu za Hopcroft-Karpův zlepšíme čas na O(|E|√|M|) = O(N√N).

Zvláště zvědaví mohou pokračovat ve čtení a dozvědět se, co dělat v případě, že máme abecedu opravdu velkou.

Velké abecedy

Pokud bychom předchozí postup chtěli zkusit např. s Unicode, náš graf by měl řádově 232 vrcholů, do většiny z kterých by žádná hrana nevedla. Nabízí se vytvářet vrcholy pouze pro zkratky, které mohou z nějakého slova vzniknout. Kolik jich bude? Ze slova délky L lze vytvořit až řádově L2 zkratek (pokud jsou všechna jeho písmena různá). Tedy náš graf může obsahovat až O(S2) vrcholů a O(NS2) hran.

To je pořád docela dost, jak pro časovou (O(N2S2)), tak paměťovou (O(NS2)) náročnost našeho algoritmu. Obojí zkusíme zachránit drobnými úpravami párovacího algoritmu.

Pokud jej neznáte, teď je vhodná chvíle to napravit. Pokud ano, pro jistotu zopakujeme drobné shrnutí a trochu terminologie: (ne)párovací hrana je hrana grafu (ne)patřící do aktuálního párování, volný vrchol je takový, který není spárován (všechny hrany s ním incidentní jsou nepárovací), střídavá cesta je cesta v grafu, na které se střídají párovací a nepárovací hrany, a nakonec zlepšující cesta (Příznivci tokového párování: rozmyslete si, že takováto definice zlepšující cesty přesně odpovídá tokové zlepšující cestě v párovací síti – jen s useknutými hranami vedoucími ke zdroji a stoku (neb v našem grafu žádný zdroj a stok nemáme).) (též volná střídavá cesta) je střídavá cesta začínající a končící volným vrcholem (a tedy nutně i nepárovací hranou). Algoritmus začne s prázdným párováním a v každém kroku najde zlepšující cestu, změní po celé její délce párovací hrany na nepárovací a naopak, čímž zachová korektnost párování a zvětší jej o jedničku. Pokud zlepšující cesta neexistuje, párování je maximální.

Klíčovým pro nás bude jedno pozorování: po celou dobu běhu algoritmu je většina grafu „nezajímavá“, totiž tvořená volnými zkratkami. „Zajímavých“ vrcholů je jen O(N) (N slov a nejvýše N spárovaných zkratek). Tedy v zajímavé části grafu je nejvýše O(N2) hran. Graf si lze představit takto:

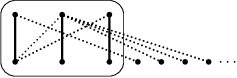
Nejprve napravíme čas. Všimneme si, že každá zlepšující cesta má lichou délku, a tudíž spojuje vrcholy z opačných partit. Stačí nám tedy hledat zlepšující cesty pouze z vrcholů v levé partitě. Dále si uvědomíme, že skoro celé hledání zlepšující cesty probíhá v zajímavé části grafu. Jakmile se dostaneme do nezajímavé části, narazili jsme na volný vrchol, a tedy konec zlepšující cesty. Při libovolném hledání zlepšující cesty tedy navštívíme libovolné množství vrcholů ze zajímavé části grafu, ale nejvýše jeden z nezajímavé. Takové hledání tedy bude trvat O(N2). A použijeme-li odhad složitosti O(čas na nalezení zlepšující cesty·|M|), dostáváme čas O(N3).

Nyní co s pamětí? Pomoci by nám mohl obvyklý trik na úlohy, které řešíme sestavením vhodného grafu: nebudeme jej v paměti vytvářet celý najednou. Místo toho, kdykoli se bude párovací algoritmus chtít podívat na nějakou část našeho grafu, tak mu ji „na požádání“ sestavíme. Co musíme umět s naším „grafem“ provádět, aby párovací algoritmus fungoval?

  1. Pamatovat si, která hrana je aktuálně v párování a která ne, umět do párování hranu přidat/odebrat.
  2. Umět vyjmenovat sousedy daného vrcholu.
  3. Umět o vrcholu poznat, zda je volný.

Stačí nám si mimo samotného grafu pamatovat nějaké jiné datové struktury, které budou umět na takovéto dotazy rychle odpovídat. Pak prostě párovací algoritmus upravíme tak, aby kdekoli původně přistupoval přímo k paměťové reprezentaci grafu, místo toho použil tyto naše struktury.

Najít sousedy daného slova je jednoduché: prostě vyzkoušíme všechny možnosti volby prvního písmene a pro každou z nich všechny možnosti volby druhého písmene, dostávajíce všechny možné zkratky v čase O(1) na každou. Ovšem obráceně (najít sousedy zkratky, tedy všechna slova, ze kterých ji lze utvořit) to vůbec není jednoduché.

Naštěstí si všimneme, že to vůbec nepotřebujeme. Hledáme pouze volné střídavé cesty, a pokud začneme zleva, půjdeme na takové cestě doprava vždy po nepárovací hraně a doleva vždy po párovací. Stačí nám tedy umět hledat:

A to už zvládneme snadno. Naše reprezentace bude vypadat následovně:

Prostřednictvím těchto informací již dokážeme „simulovat“ náš graf s logaritmickým či průměrně konstantním zpomalením. Vzhledem k tomu, že žádné párování není větší než N, spotřebujeme O(N) paměti na pomocné slovníky, ale nesmíme zapomenout na O(S) pro vstup, tedy celkem O(S). Výsledný algoritmus poběží v čase O(S + N3 log N).

Hopcroft-Karp a velké abecedy

I pro velké abecedy bychom rádi použili Hopcroft-Karpův algoritmus. Ovšem jen pokud na něm dokážeme provést optimalizace obdobné těm výše – v původní podobě by byl pomalejší než předchozí algoritmus.

Hopcroft-Karp se skládá z fází: v každé najde v inkluzi maximální množinu disjunktních nejkratších zlepšujících cest a všechny použije ke zvětšení párování. Provádí to tak, že si nejdřív pomocí BFS rozdělí vrcholy grafu do vrstev podle délky nejkratší střídavé cesty vedoucí do nich z nějakého volného vrcholu levé partity a pak už jen pomocí DFS vysbírává nejkratší cesty a značkuje vrcholy, aby žádný nepoužil dvakrát. Obě prohledávání začínají ve volných vrcholech levé partity.

Kromě grafu samotného, na který si vystačíme se strukturami popsanými dříve, si navíc potřebujeme pamatovat ještě:

Obojí budeme uchovávat ve slovnících a s každou částí se vypořádáme trochu jinak.

BFS začínáme v zajímavé části grafu. Jakmile poprvé navštívíme nezajímavý vrchol, prohledávání ukončíme. Tak určitě doběhne v O(N2), jen některým vrcholům v ℓ-té (kde ℓ je délka nejkratší zlepšující cesty) vrstvě bude chybět ohodnocení (díky čemuž si též vystačíme s O(N) paměti). To ale vůbec nevadí. Prostě jen při DFS budeme ochotni navštěvovat neohodnocené sousedy vrcholů v (ℓ- 1)-ní vrstvě a chovat se k nim, jako by ležely v ℓ-té vrstvě.

Nyní k DFS: Každá navštívená volná zkratka znamená novou nalezenou zlepšující cestu. Těch ovšem najdeme za jednu fázi nejvýše N, navštívíme tedy jen O(N) nezajímavých vrcholů a hran. To opět znamená, že si vystačíme s O(N2) času na DFS část jedné fáze a O(N) paměti pro značky.

Hopcroft-Karpův algoritmus běží v čase O(Tf√|M|), kde Tf je čas strávený jednou fází a |M| je velikost výsledného párování. V předchozích odstavcích jsme ukázali, že Tf = O(N2 log N) (použijeme-li jako slovník vyvážené vyhledávací stromy), již dávno víme, že |M| ≤ N a ještě potřebujeme O(S) na načtení vstupu. Výsledná složitost tedy bude O(S + N2√N log N) a stále si vystačíme s O(S) paměti. V praxi by nejspíš bylo výhodnější reprezentovat slovníky jako hešovací tabulky.

Program (Python)

Filip Štědronský

26-2-7 Čištění kmene (Zadání)

Nejdříve se podíváme na to, jakým způsobem může vypadat výsledný pohyb humanoidů. Nahlédneme, že existuje optimální řešení splňující tyto vlastnosti:

Zkusme nyní zodpovědět otázku, zda je možné kmen vyčistit, pokud budeme mít k dispozici k kroků. Postupovat budeme následovně: Pokud má nejlevější humanoid nějakou nečistotu nalevo od sebe, tak ji určitě musí vyčistit on. Tedy začátek jeho intervalu bude l kroků nalevo od něj – tam kde daná nečistota leží. Pravý konec jeho intervalu bude r kroků napravo od něj, přičemž chceme, aby r bylo co největší.

Humanoid má dvě možnosti:

Celkově má udělat k kroků, takže bude platit buď 2l+r = k, nebo l + 2r = k. Z těchto dvou rovnic vybereme tu, jejíž řešení má větší r. Pokud ani jedna rovnice nemá řešení s r≥ 0, tak nejlevější nečistotu za k kroků vyčistit nemůžeme, tedy pro tuto hodnotu k řešení neexistuje.

Pokud alespoň jedna z rovnic řešení pro r má, tak smažeme všechny nečistoty do l kroků nalevo od humanoida a do r kroků napravo od humanoida a stejným způsobem pokračujeme výpočtem u dalšího humanoida zleva. Pokud po zpracování posledního humanoida budeme mít vyčištěné všechny nečistoty, tak jsme našli řešení, které funguje pro k kroků.

Nyní si stačí všimnout, že pokud úloha má řešení pro k kroků, tak určitě má řešení i pro k+1 kroků. Naopak pokud úloha nemá řešení pro k kroků, tak určitě nemá řešení ani pro k-1 kroků. Optimální k tedy můžeme nalézt binárním vyhledáváním.

Maximální počet kroků, který má smysl uvažovat, je dvakrát rozdíl nejmenší a největší souřadnice na vstupu, protože určitě nepůjdeme víc jak tam a zpátky. Označme tuto hodnotu X.

Pak binární vyhledávání udělá maximálně O(log X) kroků; každý zabere čas O(H+M), kde H je počet humanoidů a M je počet nečistot. Poznamenejme ještě, že humanoidy i místa si na začátku musíme setřídit. Celková časová složitost tedy bude O((H+M) log X).

Paměťová složitost je O(M+H). Můžete nahlédnout do vzorového programu.

Program (C++)

Karel Tesař

26-2-8 Továrna na přepisování (Zadání)

Druhou série sice neřešilo tak moc lidí, jako sérii první, ale i tak jsem byl potěšen tím, kolik vašich řešení přišlo.

Úkol 1

Na řešení první úlohy bylo možné jít několika směry. Ukážeme si zde přepisovací program, který postupně umazává stejná čísla a zvedá první z nich. Lehce nahlédneme, že nahrazením dvou stejných čísel vedle jedním (stejným) číslem nic nepokazíme. Neklesající posloupnost zůstane neklesající a klesající také nepřestane klesat.

Pak nám už stačí jen zvedat číslo na první pozici postupně až do devítky. Po každém zvýšení nám tak potenciálně vznikne nová dvojice stejných znaků na začátku, které srazíme na jeden. Pokud bude posloupnost neklesající, tak nám tento postup v průběhu vymaže všechna čísla až na poslední. Pokud se tak stane, zahlásíme úspěch přepsáním na ANO.

Pokud je však posloupnost někde klesající, tak první číslo zvýšíme až na devítku a ještě nám za ní něco zbude. V takovém případě se jen zbavíme zbytku vstupu a na výstupu zanecháme NE.

Takový přepisovací program je uveden níže. V každém kroku (až na konstantně mnoho zvýšení prvního čísla) jedno číslo umaže, tedy běží v lineárním čase k velikosti vstupu.

00 →0
⋮
99 →9
^0 →1
⋮
^8 →9
^9$ →ANO
^9 →X
X0 →X
⋮
X9 →X
X →NE

Alternativním postupem může být naopak detekovat chyby. Neboli měli bychom pravidla pro jakoukoliv dvojici sousedních čísel ve špatném uspořádání (takových je 45) a tuto dvojici bychom přepsali na nějaký chybový znak. Potom bychom vymazali všechna čísla a pokud by nám na konci zůstal nějaký chybový znak, vypsali bychom NE. Tento postup má také lineární složitost, ale potřebuje o něco více přepisovacích pravidel.

Úkol 2

Budeme triviálně realizovat binární sčítačku. Budeme si ji držet vlevo od hvězdiček tak, aby hvězdičky přiléhaly k nejnižšímu bitu čísla. To nám umožní za každou hvězdičku k tomuto bitu přičíst +1.

Jak ale zajistit přenosy do vyšších řádů? Jednoduše, v momentě, kdy bude potřeba provést přenos, zapíšeme namísto přenosu nějaký symbol (z logiky sčítání se nabízí použít třeba symbol 2). A poté ho pomocí dalších pravidel posuneme do vyššího řádu (tedy z 1011+1 se stane 1012 a po přenosu nejprve 1020 a pak 1100).

Realizace s pomocí pravidel (a s ošetřením úvodní inicializace počítadla a prázdného vstupu) vypadá následovně:

^$ →0
^* →0*
0* →1
1* →2
^2 →10
02 →10
12 →20

Kolik kroků provedeme? Odstranění hvězdičky provedeme právě tolikrát, kolikrát byla na vstupu. Mohlo by se však zdát, že nám složitost pokazí přenosy. Stačí si ovšem uvědomit, že přenos z posledního bitu provedeme v každém druhém kroku, přenos z předposledního bitu jen v každém čtvrtém kroku a tak dále. Když posčítáme všechny přenosy, vyjde nám, že jich provedeme maximálně 2N, tedy složitost je stále lineární k délce vstupu. Pro podrobnější důkaz amortizace časové složitosti binární sčítačky nahlédněte na konec řešení minulého dílu seriálu.

Skládání programů

Pro řešení třetího úkolu si nejdříve ukážeme, jak za sebe složit libovolné dva přepisovací programy. Mějme dvě sady přepisovacích pravidel, z kterých chceme vyrobit třetí sadu tak, že nám bude vracet stejný výsledek, jako kdybychom výstup prvního přepisovacího programu použili jako vstup pro druhý.

Co se stane, pokud oba programy jen napíšeme pod sebe? Jelikož aplikace pravidel probíhá postupně, tak dokud běží první přepisovací program, nemůže se provést žádné pravidlo z druhého přepisovacího programu. Problém ale nastane ve chvíli, kdy se výpočet přehoupne do druhého programu. Jak zajistit, aby se nepoužilo žádné pravidlo z prvního programu?

Kdyby programy používaly úplně jiné sady znaků, bylo by to jednoduché (metaznaky začátku a konce řetězce můžeme také odlišit a to třeba tak, že k nim vždy přilepíme ještě nějaký další speciální znak). Tak si to pojďme zařídit.

Všechna pravidla prvního programu přeložíme tak, aby používaly nějaké jiné znaky (třeba ty samé, ale s čárkou). Poté jen potřebujeme přidat překlad znaků před vstupem do druhého programu, který je přepíše zpět na původní znaky.

Druhou nutnou věcí je přepis vstupní abecedy na čárkovanou verzi před vstupem do prvního programu (ale tak, aby se přepis nemohl opakovat po doběhnutí druhého programu). K tomu nám stačí libovolný jeden znak na vstupu, který se nevyskytne v průběhu výpočtu druhého programu, ani na jeho výstupu. Pomocí něj provedeme úvodní přepis.

V praxi budeme chtít mít všechna překladová pravidla na začátku přepisovacího programu. Spouštět je budeme jedním přepisovacím pravidlem na správném místě programu, které nám přidá do řetězce speciální přepisovací znak (rozmyslete si, proč to děláme takto a proč nemůžeme všechna pravidla přesunout na místo spouštěcího pravidla).

Výsledné spojení programů pak vypadá takto:

Umíme tedy spojit libovolné dva programy do jednoho, pokud se na vstupu prvního vyskytuje alespoň jeden znak, který v druhém programu použitý není.

Úkol 3

Poznatek o spojování programů použijeme pro řešení třetí úlohy. Idea bude taková, že si vstup nafoukneme o zkopírované verze obou čísel. První číslo opíšeme normálně, druhé číslo pozadu (aby se nejnižší bity obou čísel dostaly k sobě).

Taky předpokládejme to, že čísla nejsou prefixována nulami. Pokud by byla, můžeme přebývající nuly snadno odmazat. Stačí si zavést dvě pomocná pravidla pro levé a pro pravé číslo.

Tedy ze vstupu ve tvaru „1010#1100“ vyrobíme přepisem „1010_1010=0011_1100“. S touto verzí pak provedeme porovnání (postupným odmazáváním nejmenších bitů) a zjistíme, jestli je větší pravé nebo levé číslo. Druhé pak vymažeme a jsme hotovi.

Nejprve se zabývejme rozkopírováním. Ukážeme pravidla pro kopírování pravé části pozpátku. Druhá sada pravidel pro kopírování levé části bude podobná.

Hlavní idea je, že si vyrobíme na koncích jakési zarážky a postupně budeme znak po znaku pomocí vozíku (znaku v) převážet zkopírované znaky na správné místo. Následující sada pravidel nám přepis odstartuje:

# →y_=_Y
Y0 →0Y
Y1 →1Y
Y$ →X

Tím nám vznikne řetězec (zajímejme se teď jen o pravou stranu od =) ve tvaru _Y...X. Teď můžeme začít převážet znaky. Vždy nabereme jedno číslo u koncové značky, posuneme koncovou značku o jedna doleva a pomocí vozíku převezeme číslo těsně za _. Ve chvíli, kdy nemáme žádný vozík, si ho pořídíme a ve chvíli, kdy pravý ukazatel dojde až k _, ukazatel zahodíme.

0v0 →v00
1v0 →v01
0v1 →v10
1v1 →v11
_v0 →0_
_v1 →1_
1X →v1X1
0X →v0X0
_X →_

Tím jsme si vytvořili přepisovací program, který nám předzpracuje vstup. Nyní si vytvořme program, který nám zajistí samotné porovnání čísel.

Budeme postupně odebírat nejméně významné bity z obou čísel a porovnávat je. Aktuální stav porovnání si budeme držet mezi oběma čísly – jako =/>/< podle toho, jestli jsou čísla zatím stejná, je větší levé, nebo je větší pravé.

Je jasné, že pokud budou na obou stranách stejná čísla, stav (ať bude jakýkoliv) se nám nezmění. Jinak se nahne na tu stranu, kde je aktuálně větší číslo (významnější bit převáží nad těmi méně významnými). Pro stejně dlouhá čísla tedy máme následující pravidla:

1=1 →=
0=0 →=
1=0 →>
0=1 →<
1>1 →>
0>0 →>
1>0 →>
0>1 →<
1<1 →<
0<0 →<
1<0 →>
0<1 →<

Samostatně vyřešíme případ, že je jedno z čísel kratší jak druhé – pak je to delší určitě větší (ukážeme pravidla pro >, pro < jsou analogická):

1>_ →>_
0>_ →>_
1<_ →>_
0<_ →>_
0=_ →>_
1=_ →>_

Uprostřed nám zůstal jeden znak udávající, které z čísel je větší. Nyní stačí to menší vymazat (opět ukážeme jen pro >):

_>_ →Q
Q1 →Q
Q0 →Q
Q$ →

Spojením kopírovacího a porovnávacího programu (spojení můžeme provést, protože vstup obsahuje znak #, který druhý program nepoužívá) vznikne program řešící celou úlohu. Jelikož při přesouvání provedeme pro každý znak lineárně mnoho kroků vzhledem k délce vstupu a přesunů je lineárně mnoho, je výsledná složitost O(N2), kde N je počet znaků na vstupu.

Úkol 4

Jelikož jsme měli Turingovy stroje v minulé sérii zadané tak, že vracely pouze výsledek ano nebo ne (stavem, ve kterém skončily), tak se na tento výstup omezíme i u přepisovacích pravidel – na výstupu tedy zanecháme buď řetězec ANO nebo řetězec NE.

V případě, že by se řetězce ANO nebo NE vyskytovaly na vstupu nebo někde v průběhu výpočtu, odlišíme ty koncové tím, že pro ně použijeme speciální symboly.

Když jsme si odbyli technické detaily, pojďme se podívat na hlavní myšlenku převodu Turingova stroje na přepisovací pravidla. Následující krok Turingova stroje je vždy určený pozicí hlavy, stavem, ve kterém se stroj nachází, a aktuálním obsahem pásky. Tuto informaci budeme potřebovat nějak kódovat v řetězci.

Pozici hlavy tedy budeme reprezentovat speciálním znakem někde v řetězci. Přesněji více speciálními znaky – pro každý stav stroje jeden znak. Zaveďme si pozici hlavy tak, že tento speciální znak bude stát před znakem, na který by ukazovala hlava v Turingově stroji.

Každé pravidlo Turingova stroje má tyto části: vstupní stav, vstupní znak, výstupní stav, výstupní znak a výstupní posunutí. To ale můžeme velmi lehce přepsat do řeči přepisovacích pravidel. Například pravidlo pro stroj říkající „Pokud jsi ve stavu S a na pásce je x, přejdi do stavu T, zapiš na pásku y a posuň se doprava“ bychom mohli napsat jako: Sx → yT.

Drobným problémem je posouvání doleva (vzhledem k tomu, že náš znak pro hlavu stojí před přepisovaným znakem). Pro posun hlavy doleva si musíme vyrobit jedno pravidlo pro každý znak abecedy. Když bude # zastupovat libovolný znak abecedy, vypadá pak stejné pravidlo, jen s posunem hlavy doleva, takto: #Sx → T#y.

Tím máme hlavní část převodu hotovou. Stačí vyřešit pouze tři drobné technické detaily:

Úkol 4 – dodělávky

Zbývá zamyslet se nad složitostí. Na každou aplikaci pravidla Turingova stroje provedeme právě jednu aplikaci přepisovacího pravidla, takže by se mohlo zdát, že složitost obou bude stejná. Přepisovací programy ovšem musí na konci výpočtu smazat celý řetězec, takže pokaždé běží alespoň lineárně s délkou vstupu (kdežto Turingův stroj může skončit třeba po první aplikaci pravidla přechodem do koncového stavu).

Můžeme tedy prohlásit, že přepisovací program má stejnou složitost jako Turingův stroj, vždy ale nejméně lineární s velikostí vstupu.

Pokud bychom měli převod demonstrovat na příkladu s vyváženou posloupností z prvního dílu seriálu, tvořil by hlavní část programu pouze mechanický přepis pravidel Turingova stroje na pravidla přepisovacího programu. To jistě každý zvládne sám.

Mimo nich budeme potřebovat pravidla, která nám na začátku vloží do řetězce hlavu, a pravidla, která nám na konci vymažou zbylé znaky.

A to je milí přátelé z druhé série vše. Přeji vám hodně zdaru i v dalších dílech seriálu při potýkání se s dalšími zajímavými výpočetními modely.

Jirka Setnička