Třetí série dvacátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 26-3-1: Výklad z drahokamů
- 26-3-2: Střih látky
- 26-3-3: Grafová
- 26-3-4: Kladení pastí
- 26-3-5: Rozvrh kovárny
- 26-3-6: Trezor
- 26-3-7: Sopečné pokrytí
- 26-3-8: Zdivočelá počítadla
Čokolády
V této sérii jsme, jak už je naším zvykem, opět rozdávali čokolády. Tentokrát za to, pokud se vám podařilo získat z alespoň pěti úloh alespoň polovinu možných bodů.To se podařilo celkem devíti z vás. Shodou okolností je to právě prvních devět řešitelů v pořadí zisku bodů za tuto sérii. Gratulujeme a užijte si sladkou odměnu.
26-3-1 Výklad z drahokamů (Zadání)
Protože věštění, byť z drahokamů, je komplikovaná věc, začneme jednodušší úlohou. Budeme pro začátek hledat co největší žlutý čtverec.
Podobné úlohy se vyskytují docela často a zkušenému řešiteli už něco našeptává „dynamika“.
Každý (i největší) jednobarevný čtverec má nějaký pravý dolní roh. My si tedy pro každou pozici spočítáme největší čtverec, který od něj vede doleva nahoru a potom jen vybereme nejlepší možnost.
Pokud je aktuální pozice červená, je zřejmě výsledek 0, neboť je to největší žlutý čtverec, který se zde nachází. Naopak, pokud je žlutá, podíváme se na pozici o jedna doleva, o jedna nahoru a o jedna šikmo doleva nahoru. Z nich vybereme minimum jejich čtverců a to zvětšíme o 1 – na čem se „zarazí“ čtverec odpovídající tomuto minimu, na tom se zarazí i náš čtverec v aktuální pozici. Naopak, tím jak se čtverce sousedních políček překrývají, tak nám dají k dispozici odpovídající žlutou plochu, kterou jen aktuální pozicí rozšíříme. Zkuste si to nakreslit.
Samozřejmě, potřebujeme počítat maximální čtverce v takovém pořadí, abychom všechny tři sousedy, do kterých nahlížíme, měli již spočítané. Například po řádcích zleva doprava, stejně jako se čte.
A jako malý technický trik, abychom nemuseli řešit vykukování z pole na levém a horním okraji, připravíme si řádek a sloupeček nul jako jakýsi rámeček.
Nyní tedy, jak na naši těžší úlohu? Všimneme si, že každý šachovnicový čtverec je podčtvercem nějaké velké šachovnice takových rozměrů, jaké má celá mřížka. A tyto velké šachovnice existují právě dvě – jedna, která má vlevo nahoře žlutý drahokam, a k ní inverzní, která má vlevo nahoře červený. Celou mřížku si tedy převedeme a budeme pokládat žluté drahokamy tam, kde barva na dané pozici odpovídá první šachovnici, a červené, kde druhé. Tím jsme úlohu převedli na nalezení největšího jednobarevného čtverce – což je buď žlutý, nebo červený. Žlutý už najít umíme a nalezení červeného bude ponecháno na čtenáři.
Jak paměťová, tak časová složitost jsou lineární s velikostí vstupu. Ke každému políčku vstupu si pamatujeme konstantně mnoho informací (jeho převedenou barvu a jeho maximální čtverec doleva nahoru). Obdobně, při převodu políčka uděláme konstantně mnoho práce, a při počítání minima také koukáme jen na tři okolní políčka.
26-3-2 Střih látky (Zadání)
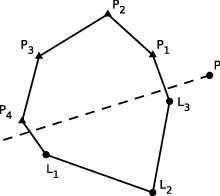
Označme si vrcholy mnohoúhelníka V0 až Vn-1 a střihovou polopřímku p (zadanou počátkem P a vektorem u). Dovolme si z úsporných důvodů zanedbat „ošklivé“ případy, kdy se polopřímka mnohoúhelníka dotýká v jednom bodě či splývá s některou jeho stranou. Nebude těžké ošetřit je dodatečně přidáním několika podmínek na vhodná místa.
Víceméně z definice konvexity plyne, že p bude mít s mnohoúhelníkem nejvýše dva průsečíky.
Všimněme si, že doopravdy vlastně chceme zjistit, se kterými stranami mnohoúhelníka se protíná. Dopočítat konkrétní souřadnice průsečíků už je pak jen drobné cvičení ze středoškolské geometrie. Pokud si s takovými úlohami nerozumíte, nastala správná chvíle přečíst si geometrickou kuchařku.
V průběhu řešení budeme často chtít vědět, jestli bod od nějaké (polo)přímky leží napravo, nebo nalevo (při pohledu po směru polopřímky). Prozatím nám uvěřte, že to snadno zjistíme v konstantním čase.
Všimněme si, že nějaká hrana mnohoúhelníka kříží p právě tehdy, když jeden její konec je vlevo od p a druhý vpravo. Dále si všimněme, že vrcholy nalevo a napravo od p tvoří v mnohoúhelníku souvislý úsek (díky konvexitě). My tedy vlastně v posloupnosti vrcholů nehledáme nic než hranici mezi levými a pravými vrcholy (díky cykličnosti existují dvě). To svádí k tomu použít něco jako binární vyhledávání.
Zde nám ovšem komplikuje život fakt, že posloupnost je cyklická a záleží
na tom, jaký vrchol vezmeme za počáteční. Uvažme např. posloupnosti
PLLPPPP a PPPPLLP.
Pouhým pohledem na prostřední prvek (v obou případech P) nepoznáme,
ve které polovině máme pokračovat v hledání.
Pokud bychom znali alespoň jeden vrchol nalevo od přímky a jeden napravo,
je to jednoduché: v těchto dvou vrcholech posloupnost rozstřihneme. Tím
vzniknou dvě posloupnosti tvaru LLLPPP či PPPLLL, v obou
z kterýchž najdeme hranici prachobyčejným binárním vyhledáváním.

Jak takové dva protilehlé vrcholy sehnat? Uvažme body V0 a Vm := Vn/2. Mohou nastat dva případy:
- V0 a Vm leží na opačných stranách p. Vyhráno.
- V0 a Vm leží na stejné straně p. Pak p neprotíná úsečku V0Vm. Ta však rozděluje mnohoúhelník na dvě poloviny – p tedy prochází jen jednou z nich. Tu druhou můžeme zahodit a pokračovat v hledání rekurzivně s mnohoúhelníkem o polovičním počtu bodů.

Algoritmus se tedy skládá ze dvou fází. V první hledáme dva body na opačných stranách p. Pokud takové dva body najdeme, přejdeme do druhé fáze. Jinak se zastavíme, až nám zbude trojúhelník, pro který už úlohu vyřešíme triviálně testem každé ze tří hran. V druhé fázi binárně hledáme hrany protínající se s p postupem popsaným výše.
V obou fázích nás každý krok stojí konstantní čas a zmenšíme jím počet zpracovávaných bodů na polovinu. Tím dosáhneme celkové složitosti O(log n).
Nalezení správné poloviny bodů
Až dosud je algoritmus docela přímočarý a vymyslitelný. Zatajili jsme ovšem jeden na první pohled drobný detail: jak z polohy p poznáme, kterou polovinu bodů (V1,…,Vm-1, nebo Vm+1,…,Vn-1) zahodit?
To překvapivě není vůbec zřejmé. Existuje spousta způsobů, jak to „umlátit“, např. počítáním nějakých vzdáleností a průsečíků. To jsou ale výpočty komplikované a nepřesné, zkusíme si proto ukázat hezčí, byť možná myšlenkově trochu náročnější řešení.
Představme si úhel V0PVm jako jakýsi „stín“. Víme, že p neleží ve stínu (jinak by se protínala s V0Vm), tedy kdykoli se nějaký objekt nachází celý ve stínu, nemá průsečík s p. Označme si S střed V0Vm a o polopřímku PS („pseudoosu“ stínu). Ta nám rozdělí rovinu na dvě poloroviny.
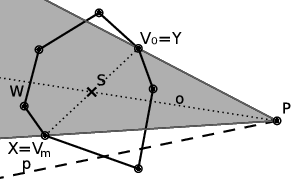
Označme si X ten z bodů V0, Vm, který leží ve stejné polorovině jako p a Y ten opačný.
Podívejme se nyní na sousedy X. Alespoň jeden z nich leží ve stínu, neb kdyby oba ležely na světle, měl by mnohoúhelník vnitřní úhel větší než 180°:
Označme si takového souseda W. Protože X, W, …, Y tvoří konvexní mnohoúhelník, musí jeho obvod „zatáčet“ pořád na stejnou stranu – na obrázku výše doprava (směrem k Y). Tedy pokud je W ve stínu, budou tam i všechny následující vrcholy (přinejmenším ty ve stejné polorovině). Tedy polovina našeho mnohoúhelníku tvořená body X, W, …, Y se nemůže protnout s p: část se jí nachází ve stínu a druhá část v opačné polorovině vůči o než p. Tyto body tedy můžeme (kromě krajních X,Y) zahodit.
Pokud jsou oba sousedé ve stínu, p nemůže mít s mnohoúhelníkem žádný průnik.
Tudíž potřebujeme umět zjistit, (1) ve které polorovině se nachází p, (2) jestli je daný soused X ve stínu.
To jsou ale jen další instance naší operace „poloha bodu vůči polopřímce“. Zvolíme si libovolný bod na p (třeba P+u) a podíváme se, na které straně je od o. Pak X je ten z V0, Vm, který leží na stejné straně. A nějaký soused X je ve stínu, právě když leží od PX na opačné straně, než X od o.
Zbývá nám nějak zařídit onu mýtickou operaci zjištění polohy bodu vůči polopřímce: mějme nějaký bod B a polopřímku q s počátkem Q a směrovým vektorem w. Nyní se nám bude hodit vektorový součin. Z pravidla pravé ruky si snadno rozmyslíte, že w ×(B - Q) je kladný právě tehdy, když B je nalevo od q, záporný, když napravo, a nulový, když leží na q.
Další (byť méně elegantní) způsob je reprezentovat si přímku rovnicí y=kx+q. Detaily necháme čtenáři k rozmyšlení.
26-3-3 Grafová (Zadání)
Požadovaný důkaz je ve své podstatě celkem jednoduchý, k dokázání použijeme matematickou indukci.
Nechť je dán graf s N vrcholy, M hranami a minimálním stupněm k. Důkaz provedeme konstrukcí, ze které nám rovnou vyplyne lineární algoritmus. Induktivně sestrojíme vhodnou posloupnost vrcholů:
- V prvním kroku zvolíme libovolný vrchol v1.
- V i-tém kroku máme již cestu z i-1 vrcholů, chceme přidat i-tý. Vybereme tedy libovolného souseda vi-1, který ještě nebyl vybrán, a zvolíme jej jako vi. Pokud takový už neexistuje, skončíme.
Nyní nahlédneme, že všichni sousedé vrcholu vr musí ležet na sestrojené cestě, neboť jinak bychom mohli cestu prodloužit a provést další krok indukce. Vrchol vr je tedy spojen hranou s aspoň k vrcholy na sestrojené cestě a tudíž určitě existuje vrchol vs, který je sousedem vr a pro který platí s ≤ r-k. Nyní už můžeme jásat, neboť vrcholy vsvs+1… vr nám tvoří kružnici délky alespoň k+1.
Postup užitý v důkaze můžeme implementovat přímo jedním průchodem grafu do hloubky, což nám dává časovou i paměťovou složitost O(N+M).
26-3-4 Kladení pastí (Zadání)
Snažíme se rozmístit pasti v pralese. Přitom musíme dodržet pravidlo, že každá pěšinka spojující dvě křižovatky sousedí alespoň s jednou pastí. V řeči teorie grafů křižovatku nazveme vrchol a pěšinku hrana. Rozmístění pastí splňující výše popsanou podmínku se obvykle nazývá vrcholové pokrytí. Na stavbu pasti v každém vrcholu musíme vynaložit úsilí Ui (zaplatit cenu). Hledáme proto takzvané minimální vážené vrcholové pokrytí.
Podívejme se nejprve na řešení lehčí varianty, ve které je graf tvořen jedinou cestou. Postup potom dokážeme zobecnit i pro těžší verzi.
Lehčí varianta
Pro každou z křižovatek máme dvě možnosti. Buď na ni past umístíme, nebo neumístíme. Pro N vrcholů je tedy všech možných rozmístění pastí 2N. Některá z těchto rozmístění samozřejmě nejsou vrcholová pokrytí. Každopádně ani tak není v našich silách vyzkoušet všechny možnosti.
Co kdyby nás pro začátek nezajímalo samotné rozložení pastí, ale pouze celková minimální cena? Zkusme ji počítat postupně pro jednotlivé počáteční úseky cesty délky i. (Délku budeme měřit třeba v počtu vrcholů.)
Zvlášť si zapamatujeme minimální cenu pi tohoto počátečního úseku délky i za podmínky, že v posledním (i-tém) vrcholu nalíčíme past. Naopak ni bude značit cenu začátečního úseku délky i v případě, že v i-tém vrcholu past není. Celkovou minimální cenu tohoto úseku cesty snadno spočteme jako min(pi, ni).
Pro první vrchol určíme minimální ceny jednoduše: p1 = U1 a n1 = 0. Pro ostatní využijeme toho, co jsme spočítali dříve. Ceny tedy budeme počítat postupně pro všechna i od 1 do N. Pokud je v i-tém vrcholu past, tak minimální cenu pi spočteme z celkové minimální ceny předchozího úseku jako pi = min(pi-1, ni-1) + Ui. V případě, že past do vrcholu i neumístíme, tak jsme ji museli umístit do předchozího vrcholu i-1. Platí tedy, že ni = pi-1.
Tímto postupem snadno v lineárním čase O(N) spočteme minimální cenu potřebnou k rozmístění pastí. Původně jsme však chtěli minimální vrcholové pokrytí i najít. Zrekonstruujeme jej v opačném pořadí od N do 1.
Pokud se rozhodujeme, zda použít i-tý vrchol, pak jej vybereme tehdy, když se nám to vyplatí. Tedy když platí pi ≤ ni. Pokud však vrchol nevybereme, nutně musíme vybrat vrchol i-1. V tom případě se znovu rozhodujeme až u vrcholu i-2.
Těžší varianta
Jak postupovat v případě, že cestičky a křižovatky tvoří strom? Minimální ceny chceme opět počítat postupně z předchozích mezivýsledků. Představme si celý strom jako zakořeněný (všechny vrcholy kromě kořene mají jednoznačně určeného otce). Minimální ceny pi a ni pak budeme počítat pro všechny podstromy, tj. pro vrchol i se všemi jeho potomky.
Potřebné pořadí pro postupné počítání cen získáme tak, že projdeme celý strom pomocí algoritmu prohledávání do hloubky. Při opuštění vrcholu spočteme ohodnocení pi a ni jeho podstromu následovně:
- Pokud je vrchol i list, nastavíme minimální cenu s použitím daného vrcholu pi = Ui.
- Cena bez umístění pasti do listu potom bude ni = 0.
- Pro ostatní vrcholy určíme minimální cenu s použitím pasti ve vrcholu i
jako součet ohodnocení daného vrcholu a celkové minimální ceny podstromů všech
jeho synů: pi = Ui + ∑j ∈Syn(i) min(pj, nj),kde Syn(i) značí množinu synů vrcholu i.
- Pokud do vrcholu i past neumístíme (dle předchozího bodu), musíme pasti
nalíčit ve všech jeho synech: ni = ∑j ∈Syn(i) pj.
Při opouštění posledního vrcholu tak spočítáme minimální cenu rozmístění pasti v celém stromě.
Stejně jako v lehčí variantě musíme ještě určit, ve kterých vrcholech máme pasti nalíčit, abychom dodrželi spočítanou minimální cenu. Projdeme tedy znovu náš strom. Na křižovatku i past umístíme, pokud opět platí pi ≤ ni. Když však past do vrcholu neumístíme, musíme ji přidat do všech jeho synů.
Tím máme i pro těžší variantu celkem slušnou časovou a paměťovou složitost O(N). Strom pouze dvakrát projdeme. Přidané výpočty sice závisí na počtu synů daného vrcholu, dohromady je však synů stejně jako vrcholů.
Pro (NP-)úplnost ještě dodejme, že pro obecný graf není v současnosti známé žádné efektivní řešení.
Program (C++) – lehčí varianta
Program (C++) – těžší varianta
26-3-5 Rozvrh kovárny (Zadání)
Až na pár originálních řešení, často fungujících a optimálních, zvolili všichni hladový přístup zezadu, čili hladový algoritmus, který si popíšeme. Stručně řečeno: seřadíme si požadavky dle termínu dokončení, bereme je od nejvyšší hodiny dokončení po nejmenší a dáváme do rozvrhu do nejvyšší volné hodiny tak, že vždy bereme nezařazený požadavek s nejvyšší prioritou, který lze v tu hodinu vyrábět.
Jak vybírat požadavek s nejvyšší prioritou? Řešení napovídal symbol kuchařky u zadání odkazující se na kuchařku o haldách. Na požadavky použijeme haldu, konkrétně maximovou, tedy řazenou od největšího prvku po nejmenší. Náš algoritmus tedy bude takový hladový.
Trochu podrobněji: Nejprve si seřadíme požadavky dle termínu dokončení a zavedeme si proměnnou hodina, což bude poslední možná hodina, do níž můžeme rozvrhnout požadavek, a kterou zinicializujeme na maximální hodinu dokončení nějakého požadavku mínus jedna. Pak bereme požadavky sestupně dle hodiny dokončení.
V každé iteraci se nejprve podíváme, jestli mezi požadavky nejsou nějaké s termínem hodina + 1 (plus jedna kvůli tomu, že s výrobou nástroje musíme začít hodinu před termínem). Všechny takové přidáme do haldy. Pak vybereme z haldy požadavek s nejvyšší prioritou, rozvrhneme vybraný požadavek na hodinu hodina a tuto proměnnou snížíme o jedna. Skončíme, když se hodina dostane pod nulu.
Počet iterací je roven největší hodině dokončení H mezi požadavky. H však není polynomiální v N, ani v délce vstupu, náš algoritmus tedy není ani polynomiální. Nejčastější chybou v řešeních právě bylo, že skončila s algoritmem, který závisel na H.
Oprava na polynomiální algoritmus je však nasnadě: pokud je halda prázdná, rovnou posuneme proměnnou hodina na nejvyšší hodinu dokončení nezpracovaného požadavku mínus jedna. Díky tomu v každé iteraci odebereme jeden prvek z haldy a přidáme ho do rozvrhu. Alternativně je možné na začátku inicializovat proměnnou hodina na N a všimnout si, že si tím nic nepokazíme, protože stejně nebudeme vyrábět více jak N hodin.
Seřazení dle hodin dokončení jistě zvládneme v O(N log N), kde N je počet požadavků. Z kuchařky víme, že haldové operace jako přidávání, nalezení největšího prvku a jeho smazání trvají logaritmus z velikosti haldy, která bude v nejhorším případě obsahovat všech N požadavků.
V každé iteraci vybereme z haldy maximum (za O(log N)) a smažeme ho, můžeme ale do haldy přidat hodně požadavků. Každý požadavek však dáme do haldy jen jednou, což celkově dává O(N log N) času na přidávání. Časovou složitost jsme tedy určili na O(N log N). Co se týče paměti, vystačíme si jistě s prostorem O(N).
Důkaz správnosti
 Zbývá už jen dokázat, že náš algoritmus dává optimální rozvrh, tedy že
nelze udělat rozvrh s větším součtem priorit. Budeme postupovat sporem, tedy
předpokládat, že pro nějaký seznam požadavků existuje lepší rozvrh než ten, jež
našel náš algoritmus. Postupně dojdeme k nějaké zjevné nepravdě, což znamená, že
lepší rozvrh neexistuje.
Zbývá už jen dokázat, že náš algoritmus dává optimální rozvrh, tedy že
nelze udělat rozvrh s větším součtem priorit. Budeme postupovat sporem, tedy
předpokládat, že pro nějaký seznam požadavků existuje lepší rozvrh než ten, jež
našel náš algoritmus. Postupně dojdeme k nějaké zjevné nepravdě, což znamená, že
lepší rozvrh neexistuje.
Rozvrh R1 vytvořený naším algoritmem a lepší rozvrh R2 se musí někde lišit, přičemž nás zajímají jen rozdíly v prioritách požadavků pro konkrétní hodiny. Jelikož R2 má vyšší součet priorit, musí existovat hodina H, ve které má lepší rozvrh požadavek P s vyšší prioritou, než má požadavek zpracovávaný v hodině H v našem rozvrhu.
Provedeme výměnu a upravíme lepší rozvrh R2 na podobný rozvrh se stejným součtem priorit. Požadavek P musíme vyrábět v našem rozvrhu R1 v hodině H', kde H' > H, jinak bychom ho v hodině H vytáhli z haldy. Nyní zaměníme v rozvrhu R2 požadavky v hodinách H a H' a všimneme si, že jsme si nepokazili rozvrh: požadavek z hodiny H' vyrábíme dříve a požadavek z hodiny H lze v našem rozvrhu vyrábět v hodině H', takže to musí jít i v rozvrhu R2.
Jelikož upravený rozvrh R2 má vyšší součet priorit než R1, tak i po výměně musí existovat hodina, v níž se v R2 vyrábí požadavek s vyšší prioritou než v R1. Mohli bychom tedy takovéhle výměny provádět donekonečna, což však nejde, neboť po každé výměně vzroste alespoň o jedna počet hodin, kde se shodují rozvrhy R1 a R2, konkrétně o hodinu H'. Čili máme kýžený spor.
Tím jsme úspěšně vykovali algoritmus. Užijte si zbytek zimy … tedy, chtěl jsem říct jara.
26-3-6 Trezor (Zadání)
Všichni, kdo se pokusili o tuto úlohu, se nezastavili u lehčí verze a rovnou se pustili do verze plné. Přesto se na chviličku u lehké verze zastavme, uvidíme, že se dá řešit pěkným trikem.
V lehčí verzi nám jednotlivé vnitřní klíče dají dohromady číslo ve dvojkovém zápise – sérii jedniček a nul – a my chceme všechny nuly změnit na jedničky. To určitě můžeme udělat tak, že použijeme právě klíče s exponenty odpovídající pozicím nul v tomto čísle. Nejde to však lépe, s menším počtem klíčů, než kolik je v čísle nul?
Nejde. Žádným způsobem totiž přidáním jednoho klíče nezměníme více než jednu nulu na jedničku. I když by došlo k „přetečení“ nějakého řádu, tak se nám na tomto místě objeví nula a zbytek čísla se chová stejně, jako kdybychom jedničku přičítali k o jedna většímu řádu. Zadání úlohy se tedy dá přeformulovat přímo na spočítání počtu nul ve dvojkovém zápisu součtu vnitřních klíčů.

Protože se nám v lehčí variantě stejné klíče neopakují, tak rovnou dostaneme číslo ve dvojkové soustavě, kde počet jedniček odpovídá počtu vnitřních klíčů. Stačí tedy v lineárním čase a konstantní paměti při čtení vstupu najít největší exponent vnitřního klíče a odečíst od něj celkový počet vnitřních klíčů, čímž rovnou dostaneme potřebný počet vnějších klíčů.
Při řešení těžší varianty ale již bude potřeba hodnoty klíčů nějak sčítat. Nemusíme operovat přímo s hodnotami, bohatě nám stačí sčítat exponenty. Označme si pomocí N počet exponentů (vnitřních klíčů) na vstupu a jako M maximální exponent, který se na vstupu může vyskytnout. Podle velikosti M můžeme úlohu řešit dvěma různými způsoby:
Pro malé M, pokud M < N log N, je nejvýhodnější použít přihrádkové třídění. Maximální exponent, ke kterému se můžeme v průběhu výpočtu dostat, je M + log N (kdyby všech N vnitřních klíčů bylo maximálního exponentu), takže si vyrobíme takto velké pole přihrádek a pak v lineárním čase spočítáme počty jednotlivých exponentů na vstupu.
Pak nám stačí toto pole projít odzadu, počítat počet nul, a kdykoliv se nám v nějaké přihrádce vyskytne číslo větší jak jedna, tak ho necháme „přetéct“ – v aktuální přihrádce necháme zbytek po dělení dvěma (tedy buď 0, nebo 1) a do další přihrádky přičteme (celočíselnou) polovinu hodnoty z aktuální přihrádky. Tím úlohu vyřešíme v čase O(N + M) a s pamětí O(M + log N).
Pro velká M (klidně řádově větší jak N) by se nám však již pole přihrádek do paměti vůbec nemuselo vejít, nemluvě o tom, že by v něm mohly být velké „díry“, ve kterých bychom trávili zbytečně moc času. Pak je výhodnější zvolit jiný postup.
Všech N vnitřních klíčů si můžeme na začátku programu v čase O(N log N) seřadit, seřazené naskládat do spojového seznamu, a pak ho opět jako v předcházejícím případě projít od nejmenšího. Zde však bude drobný rozdíl v tom, že pokud ve spojovém seznamu ještě položka pro další exponent není, tak ji založíme. V tomto případě se dostáváme na časovou složitost O(N log N) (nejdéle trvá úvodní setřídění) a paměťovou O(N).
Poznámka: V ukázkovém programu je použit navíc trik, díky kterému se bez spojáku nakonec obejdeme úplně. Stačí si při průchodu jen pamatovat, kolik stejných exponentů jsme v seřazeném poli už potkali. Kdo chcete, nahlédněte.
26-3-7 Sopečné pokrytí (Zadání)
Naším úkolem je pro mapu R ×S najít posunutí mřížky s velikostí buňky A ×B takové, že počet buněk obsahujících alespoň jeden sopečný kráter je minimální. K takovému výpočtu se nám bude hodit umět rychle zjišťovat, jestli nějaký konkrétní obdélník o velikosti A ×B obsahuje sopečný kráter.
My si ukážeme, jak v čase O(RS) vyrobit strukturu, pomocí které v čase O(1) dokážeme zjistit počet kráterů v libovolném podobdélníku, speciálně tedy i v podobdélnících A ×B.
Jedná se o takzvané dvourozměrné prefixové součty. Mohli jste je potkat například v kuchařce o základních algoritmech. Pokud nepotkali, nevadí, myšlenku zde zopakujeme:
Pro každé políčko si předpočítáme, kolik kráterů obsahuje horní levý obdélník, který má pravý dolní roh právě v tomto políčku. Tedy políčko na pozici [x,y] bude mít hodnotu počtu kráterů v obdélníku ([1,1], [x,y]). Tento výpočet si můžete sami rozmyslet, nebo se na něj podívat ve zdrojovém kódu – není to nic těžkého.
Dvourozměrné pole dvourozměrných prefixových součtů si označme P, pak počet kráterů v obdélníku ([a,b], [c,d]) získáme jako:
Když již máme vybudovanou pomocnou datovou strukturu, zkusíme každé možné posunutí větších buněk. Každé políčko se právě jednou stane nějakým pravým dolním rohem buňky (pro právě jedno posunutí).
V praktické realizaci tak pro každé políčko v mapě R ×S zjistíme, jestli obdélník A ×B mající pravý dolní roh v tomto políčku obsahuje kráter a pokud ano, tak k příslušnému posunutí mřížky přičteme jedničku. Tím jsme vlastně hotovi, už se jen stačí podívat, při jakém z A ×B posunutí jsme potřebovali nejméně buněk mřížky.
Časová i paměťová složitost algoritmu je O(RS). Můžete se také podívat do vzorového kódu psaného v jazyce C++.
26-3-8 Zdivočelá počítadla (Zadání)
Úkol 1 – aritmetické instrukce
Začneme zkratkou ADD x,y,z pro uložení součtu x+y do registru z.
Nejprve zkopírujeme x do z a y do pomocného registru t. Poté budeme
postupně dekrementovat t a inkrementovat z.
MOV x,z
MOV y,t
JZ t,Y
X: INC z
DEC t
JNZ t,X
Y:
(Všimněte si, že naše zkratka nepotřebuje, aby registry x, y a z byly
navzájem různé. O to se budeme snažit i u ostatních aritmetických operací.
Jen musíme dodefinovat MOV x,x, aby neprovedl nic.)
S odčítáním SUB x,y,z si poradíme podobně. Nezapomeneme
na případ, kdy x<y, na což máme podle zadání odpovědět nulou.
MOV x,z
JZ y,Y
MOV y,t
X: DEC z
DEC t
JNZ t,X
Y:
Násobení MUL x,y,z pak definujeme jako opakované sčítání
(s je další pomocný registr):
CLR z
JZ y,Y
MOV y,s
X: ADD x,z,z
DEC s
JNZ s,X
Y:
Ještě se nám v následujících úkolech bude hodit dělení DIV x,y,p,q,
které do p uloží celou část podílu x/y a do q zbytek po tomto dělení.
Implementujeme jako opakované odčítání, jen pokaždé odečteme y-1 a před
odečtením zbývající jedničky zkontrolujeme, zda se dělenec už nevynuloval.
MOV x,t
CLR p
MOV y,s
DEC s ; s = y-1
X: MOV t,q
SUB t,s,t
JZ t,Y
DEC t
INC p
JMP X
Y:

Úkol 2 – tradiční závorky
Závorky na vstupu dostaneme zakódované do jednoho velkého čísla. To potřebujeme rozebrat na desítkové číslice, což se daleko snáz dělá od konce než od začátku: vydělením deseti odstraníme poslední číslici, zbytek nám řekne, jaká číslice to byla.
Na samotnou kontrolu uzávorkování použijeme jako obvykle počítadlo, ale jelikož
vstup zpracováváme zprava doleva, bude tentokrát udávat, kolik závorek bylo
uzavřeno, ale ještě ne otevřeno. Za každou ) ho tedy zvýšíme o 1 a
za každou ( snížíme. Nesmí přitom nikdy klesnout pod nulu a na konci
vstupu musí vyjít nulové.
S našimi aritmetickými instrukcemi je implementace hračka. V registru x očekáváme vstup, do y zapisujeme výstup, z nám bude počítat závorky, v d bude uložena konstanta 10 a r bude obsahovat právě odebranou číslici.
CLR y ; zatím špatně
CLR z ; počítadlo závorek
CLR d
INC d (10x) ; d=10
NEXT: JZ x,END
DIV x,d,x,r ; další závorka?
DEC r
JZ r,OPEN
INC z ; zavírací
JMP NEXT
OPEN: JZ z,DONE ; otvírací
DEC z
JMP NEXT
END: JNZ z,DONE ; závěrečný test
INC y ; správně
DONE:
Úkol 3 – simulace Turingova stroje
Nejprve využijeme trik z 1. série, abychom daný Turingův stroj převedli na jednopáskový.
Nyní navrhneme, jak do registrů zakódovat konfiguraci stroje. Abecedu stroje očíslujeme od 0 do nějakého A-1, přičemž 0 bude znamenat mezeru. Pásku rozdělíme v místě hlavy. Levou část uložíme do registru ℓ jako číslo v soustavě o základu A, číslice nejnižšího řádu bude odpovídat znaku těsně před hlavou (zde se hodí, že 0 je mezera, takže vlevo přirozeně vznikne nekonečně mnoho mezer). Znaky vpravo od hlavy zakódujeme obdobně do registru r, nejnižší řád bude odpovídat znaku bezprostředně za hlavou.
Zbývá nějak reprezentovat znak, na kterém právě stojí hlava, a aktuální stav řídicí jednotky stroje. To zakódujeme do pozice v počítadlovém programu, kde se zrovna nacházíme. Program bude tvořen velikost abecedy × počet stavů podobnými bloky, změna stavu nebo aktuálního znaku bude pouhý skok do jiného bloku.
Stačí tedy umět posouvat hlavu. Popišme posun doprava: Aktuální znak se přesune do levé části pásky, takže registr ℓ vynásobíme velikostí abecedy a přičteme aktuální znak. Naopak registr ℓ vydělíme velikostí abecedy a zbytek nám řekne, jaký znak se stal aktuálním. Posun doleva vyřešíme obdobně.
Úkol 4 – redukce počtu registrů
Kdyby nám stačilo dokázat, že stačí nějaký pevný počet registrů, můžeme k tomu použít předchozí úkol. Ze zadání víme, že každý počítadlový program lze přeložit na ekvivalentní Turingův stroj, v předchozím úkolu jsme se naučili převést ho zpět. Kombinací obou převodů získáme počítadlový program s pevným počtem registrů. Kdybychom promysleli detaily (zejména počty pracovních registrů v aritmetických instrukcích), dostali bychom se na něco jako 5 registrů. Ukážeme, že stačí méně.
Mějme program, který používá registry r1,… ,rk. Jejich stav dovedeme zakódovat do jediného čísla
| r1 |
| 1 |
| rk |
| k |
kde p1,… ,pk jsou navzájem různá prvočísla. Z jednoznačnosti prvočíselného rozkladu plyne, že zakódovaný stav lze dekódovat jediným možným způsobem.
Instrukci INC ri přeložíme na násobení registru r prvočíslem pi.
Ačkoliv bychom mohli použít zkratku MUL, raději si násobení naprogramujeme sami
využívajíce toho, že pi je konstanta. Bude nám stačit jediný pracovní registr t.
CLR t
X: INC t (p_i-krát)
DEC r
JNZ r,X
Y: INC r ; přelijeme zpět do r
DEC t
JNZ t,Y
Podobně DEC ri přeložíme na dělení registru r číslem pi, ovšem musíme
si dát pozor, abychom v případě, kdy r není dělitelné, vše vrátili do původního stavu.
CLR t
; Opakovaně odčítáme p_i.
DIV: JZ r,OK
DEC r
JZ r,R1
DEC r
JZ r,R2
(... dalších p_i-3 dvojic ...)
DEC r
INC t
JMP DIV
; Nebylo to dělitelné,
; pozice v programu udává zbytek.
(... p_i-3 inkrementů jako níže ...)
R2: INC r
R1: INC r
; Nakonec k r přičteme t * p_i.
T: JZ t,DONE
INC r (p_i-krát)
DEC t
JMP T
; Povedlo se, přelijeme zpět do r,
; které už je touto dobou nulové.
OK: INC r
DEC t
JNZ t,OK
DONE:
Podmíněný skok JNZ vyřešíme obdobně: pokusíme se o DEC, pokud
se povede, zvrátíme jeho účinek dalším INC a skočíme. Pakliže se
nepovede, jen uvedeme registr r do původního stavu a pokračujeme
v programu.
Vypadá to tedy, že každý program dokážeme upravit, aby mu postačily pouhé dva registry r a t. Jenže ouha: ještě musíme umět zakódovat vstup do našeho „exponenciálního“ kódování, a na konci programu zase dekódovat výstup. K tomu bohužel potřebujeme další registr.
Kódování vstupu bude probíhat tak, že na počátku položíme r=1 a pak budeme dekrementovat vstupní registr a přitom inkrementovat jeho zakódovaný obraz v r. Podobně dekódování bude dekrementovat zakódovaný obraz výstupního registru a inkrementovat skutečný výstupní registr. Na obojí nám postačí tři registry.
Dodejme ještě, že je známo, že se dvěma registry takové kódování provést nelze. Důvod je prostý: nelze spočítat žádnou funkci, která roste exponenciálně. Dvojregistrový stroj tedy nemůže být univerzální. (Důkaz viz Rich Schroeppel: "A Two-counter Machine Cannot Calculate 2N", Massachusetts Institute of Technology, Artificial Intelligence Memo #257.)
Úkol 5 – minimální instrukční sada
Někteří řešitelé dokázali vymyslet jednoinstrukční sadu, ale pokaždé nějakým ošklivým trikem. Třeba instrukcí, jejíž součástí je konstanta, která instrukci řekne, jakou operaci má provést. Zde předvedeme také mírně podlé, ale snad o ždibec elegantnější řešení.
Naše instrukce se bude jmenovat IDJNZ x,y,p (increment, decrement
and jump if not zero) a bude fungovat takto: Nejprve otestuje registr y
na nulu. Pak inkrementuje registr x, načež dekrementuje registr y (pokud
by vzniklo záporné číslo, zapíše nulu). Nakonec skočí na adresu p, pokud na
začátku byl registr y nenulový. V opačném případě nikam neskáče.
INC x zapíšeme jako IDJNZ x,t,p, kde t je nějaký pracovní
registr a p adresa těsně za instrukcí.
DEC x přeložíme analogicky na IDJNZ t,x,p.
JNZ x,p upravíme na IDJNZ x,x,p.