Třetí série dvacátého šestého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

I v této sérii můžete získat sladkou odměnu! Každému, kdo z libovolných pěti úloh dostane alespoň polovinu možných bodů, které lze za tyto úlohy získat, pošleme čokoládu.

Zadání úloh

V předchozích dvou sériích jste mohli sledovat nouzové přistání vesmírné lodi Freya. Jacob, její jediný přeživší, začal prozkoumávat neznámou planetu a pátrat po inteligentních formách života.

Hrdina příběhu ve svém pátraní uspěl a objevil celý hlouček mimozemských bytostí. Neučinil to však příliš šikovně. Poté, co si jej jeden z tvorů všiml a upozornil ostatní, se rázem na Jacoba upínaly pohledy celého hloučku mimozemských bytostí …

* * *

Dva mimozemšťané vydali zvláštní vřískot, při kterém Jacobovi ztuhla krev v žilách. Rozhodl se nic neriskovat, prudce se otočil a přešel v trysk. Terén se zde prudce svažoval. Ozvaly se další vřískoty. Zněly tak hrozivě, že Jacob na chvíli přestal dávat pozor na své kroky a nohy se mu zamotaly do lián.

Udržet balanc se mu nepodařilo a pak už šlo vše velmi rychle. Jacob ještě stihl natáhnout ruce před sebe, z pádu se tak stal kotrmelec. První kotrmelec byl vystřídán druhým, mnohem rychlejším kotrmelcem. Nežli získal příležitost jakkoliv ovlivnit dráhu svého pohybu, už se řítil dolů ze zhruba desetimetrového srázu.

Po probuzení byl Jacob oslněn červeno-žlutými světýlky, odvrátil proto svůj pohled pryč. Viděl, že se nachází v místnosti se zelenými stěnami. V místnosti se mimo té, na níž ležel, nacházely další čtyři postele. Jednalo se vlastně spíše o lenošky nežli klasické postele, na jaké byl Jacob zvyklý. Jakmile Jacob pořádně zaostřil svůj zrak, zpozoroval, že neleží v klasické místnosti, nýbrž ve velmi honosném stanu.

Vrátil se pohledem ke stropu, teď už byl schopen si prohlédnout ona světýlka. Nebyla to světýlka, ale ozdobné drahokamy odrážející záři svící rozmístěných všude po stanu. Kromě svícnů se zde nacházely zdobené zlaté oštěpy, zlaté masky a totemy. Stan působil jako sídlo šamana.

26-3-1 Výklad z drahokamů (11 bodů)

Žluté a červené drahokamy se těšily velké oblibě a mimo ozdobných účelů se využívaly i k vykládání osudu.

Při takovém výkladu se drahokamy rozsypou na zem a uspořádají do obdélníkového tvaru. Protože všechny drahokamy mají zhruba stejné rozměry, vytvoří tak čtvercovou síť.

Následně se zkoumají všemožné pravidelnosti ve vzniklém obrazci. Zvláštní význam mají uspořádání, ve kterých se drahokamy střídají jako políčka na šachovnici. Vaším úkolem je proto najít největší takovéto uspořádání.

Nyní o něco formálněji: Je zadána tabulka znaků . a # o R řádcích a S sloupcích. Nalezněte největší čtvercovou oblast, ve které jsou znaky uspořádány jako na šachovnici. Tedy v této čtvercové oblasti nikdy nesousedí dva stejné znaky celou stranou, ale pouze rohem.

Příklad: Podívejme se na následující tabulku o šesti řádcích a sedmi sloupcích:

.#....#
#.##.#.
.#.#.##
#.#.#.#
...#.#.
#.#.#.#

Největší hledaná čtvercová oblast s šachovnicovým vzorem má stranu dlouhou čtyři a svůj levý horní roh má na třetím řádku a v třetím sloupci.

Řešení

Teprve po prohlédnutí stanu si Jacob uvědomil, co se dělo před jeho probuzením. Radost z neporaněné hlavy a rukou vyhasla v momentu, kdy zjistil, že nohama nemůže nejen pohybovat, ale dokonce je ani necítí. Nezbývalo než zůstat ležet a zaposlouchat se do venkovních zvuků.

Jacob věděl pouze to, že se nachází v mimozemském táboře a stará se zde o něj trojice léčitelů. Dobře jej živili a Jacob sílil. Pomocí posunků se s nimi i poměrně dobře dorozuměl.

Po zhruba měsíci donesli léčitelé Jacobovi berle. Vyrobeny byly z precizně leštěného dřeva. Dřevo připomínalo pozemský mahagon, jen bylo mechově zelené. Rukojeti byly omotány kožešinou a z boku berlí se nacházela spousta rytin vyobrazujících souboje mimozemšťanů s divou zvěří.

Pohyb s berlemi byl obtížný, protože Jacob nohy za sebou pouze vláčel. I tak měl ohromnou radost, když se mohl začít procházet mimozemským táborem. Při jedné z prvních procházek natrefil na stan zdejších švadlen.

26-3-2 Střih látky (12 bodů)

Jacob vypomáhá švadlenám v jejich práci. Jeho prvním úkolem je stříhání látky. Pozemský pomocník je však ukrutně nešikovný a švadlenám je pro smích.

Jacobovi se daří vést střih rovně, má však velmi špatný odhad. Látku prostě nikdy neustřihne tak, jak by si představoval. Pomozte mu!

Vašemu algoritmu bude předložen konvexní mnohoúhelník zadaný posloupností vrcholů (vrcholy budou zadány v pořadí, v jakém se vyskytují na obvodu mnohoúhelníka). Jeho úkolem pak je vybudovat si datovou strukturu, se kterou bude schopen efektivně odpovídat na střihové dotazy.

V rámci jednoho střihového dotazu bude zadána polopřímka, podél které bude veden střih. Úlohou datové struktury je určit průsečíky polopřímky s mnohoúhelníkem, pokud existují.

Řešení

Následující čas v táboře ubíhal našemu hrdinovi jen pozvolna. Přes usilovnou práci léčitelů (nebo právě kvůli ní) trvalo dva roky, než byl Jacob schopen chodit bez berlí. I poté většina procházek po chvíli skončila ostrou bolestí. Až po zhruba třech a půl letech byl Jacob schopen chodit asi půl dne v kuse, než přišla ona bolest.

Jak Jacob celý ten čas trávil? Inu, zažil ještě vesmírné výpravy před kryogenickým spánkem, přečkat pár let s omezenými možnostmi pohybu a lidského kontaktu pro něj nebylo nic nového. Našel si celou paletu činností. Velké úsilí věnoval například luštění mimozemského jazyka a po zhruba třech letech byl schopen se s mimozemšťany běžně dorozumět. Zdálo se však, že čím lépe Jacob hovořil mimozemsky, tím menší chuť s ním hovořit mimozemšťané měli.

Vynechme drobné Jacobovy zážitky z těchto časů a přesuňme se raději do doby zhruba čtyř let od ztroskotání. Tehdy se Jacob poprvé odvážil vypravit pěšky až k vraku lodi UFC Freya, kdysi věhlasné nákladní lodi Spojené federace. Loď zarůstala zelení, působila však poměrně celistvě. K výbuchu poškozeného hlavního reaktoru evidentně nedošlo.

U trosek lodi potkal Jacob mimozemšťanku. Po krátké konverzaci se ukázalo, že toto není její první návštěva vraku lodi. Ada, jak se mimozemšťanka jmenovala, dle svých slov společně se svými mimozemskými kumpány získala velkou část lodní knihovny.

V luštění beletrie prý mimozemšťané příliš úspěšní nebyli. Na lodi se však nacházelo mnoho knih s informatickou a matematickou tématikou. Na základě obrázků pak odvodili význam většiny pozemské matematické notace.

Adě se prý obzvlášť líbila kniha o teorii grafů. Toho se Jacob rozhodl využít.

Při svém pobytu se bavil řešením spousty úloh, které si pamatoval ze Země, ale nikdy dřív na ně neměl dostatek času. Jednu úlohu řešil marně celé čtyři roky a třeba by Adu mohla napadnout právě ta myšlenka, která jemu unikala.

26-3-3 Grafová (9 bodů)

Nechť k je libovolné celé číslo větší než jedna. Uvažme graf, jehož všechny vrcholy mají stupeň alespoň k. Tím myslíme, že z každého vrcholu vede alespoň k hran.

Dokažte, že v takovém grafu existuje kružnice délky alespoň k+1, a sestrojte algoritmus, který nějakou takovou kružnici najde.

Řešení

Trvalo sice dlouho, než si vzájemně vyjasnili terminologii, nakonec se však dorozuměli a úlohu překvapivě svižně vyřešili.

Jacob byl setkáním s Adou doslova nadšen. Během pobytu v mimozemském táboře dávno přestal věřit, že by snad mohli existovat mimozemšťané se smyslem pro humor. Nebo nedej bože mimozemšťané, se kterými by se dalo jen tak volně povídat.

V průběhu roku se Jacob s Adou pravidelně scházeli. Zásadně vždy u onoho vraku. Tato setkání dávala Jacobovu životu na planetě smysl.

Jak se chýlil pátý rok soužití s mimozemšťany v táboře ke svému konci, dokázal Jacob pobíhat celý den po pralese, aniž by cokoliv cítil. Přišel čas zvažovat co dál. Rozhodně neměl chuť zůstávat u těchto prazvláštních mimozemšťanů. Sice se o něj pět let starali, nebyli však za celou dobu schopni si s ním rozumně promluvit a říci, co jsou zač. Na druhou stranu o Adě toho věděl ještě méně. Neměl ani to nejmenší tušení, kde a jak vlastně žije.

Během jedné noci tohoto období, kdy Jacob nevěděl kudy kam, jej ze spánku vyrušilo zašelestění. Nebral na něj žádný ohled a pouze se začal v posteli přetáčet na druhý bok. Uprostřed pohybu jej polekaly obrovské oranžové oči.

V úleku začal šmátrat po dýce, kterou měl vždy položenou u své postele. Než však pevně uchopil rukojeť dýky, rozpoznal v šepotu neznámé osoby Adin hlas.

Jacoba napadla celá řada dotazů. Než je stihl všechny vyslovit, Ada jej přerušila. „Není čas na dotazy,“ šeptala Ada, „Bratrstvo tě potřebuje.“

Jacob se omezil na jediný dotaz. Jak se bez povšimnutí a bezpečně dostanou pryč z tábora? Kolem tábora byla totiž rozmístěna spousta pastí pro zneškodnění vetřelců neznalých terénu. V noci byly tyto pasti obzvláště zákeřné.

Na to měla Ada prostou odpověď. Ukázala Jacobovi pečlivě vypracovanou mapku rozmístění těchto pastí po okolí tábora.

26-3-4 Kladení pastí (10 bodů)

V této úloze budete navrhovat algoritmus pro hledání optimálního rozmístění pastí v pralese.

Prales je neprostupný a pohybovat se lze prakticky jen po vyšlapaných pěšinkách. K dispozici máte mapu terénu. Na mapě se nachází N křižovatek a M pěšinek. Každá pěšinka spojuje dvě křižovatky.

Pro každou dvojici křižovatek existuje právě jedna cesta (posloupnost pěšinek), po které se lze přemístit z první křižovatky na druhou. V informatické řeči bychom řekli, že mapa je stromem.

Pasti umisťujeme do křižovatek. Vyžadujeme, aby pro každou pěšinku platilo, že na alespoň jedné z křižovatek, které spojuje, leží past.

Umístit past na křižovatku nemusí vždy stát stejné úsilí. Pro každou křižovatku máte zadánu hodnotu U, která modeluje míru vynaloženého úsilí.

Navrhněte algoritmus, který nalezne rozmístění pastí do křižovatek tak, aby každá pěšinka měla na alespoň jednom ze svých konců past. Součet hodnot U všech křižovatek, na které algoritmus umístí past, musí být minimální možný.

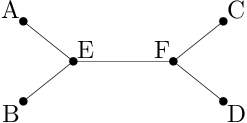
Příklad: Představte si mapu cestiček jako na následujícím obrázku. V případě, že by umístění pastí stálo na všech křižovatkách stejné úsilí, bylo by nejlepší umístit pasti na křižovatky E a F, čímž bychom pokryli všechny cestičky.

Příklad k 26-3-4

Pokud by však ohodnocení úsilí vypadalo jako U(A)=1, U(B)=1, U(C)=2, U(D)=3, U(E)=3, U(F)=4, bylo by nejvýhodnější umístit pasti na křižovatky A, B a F za celkově 6 jednotek úsilí. Žádné jiné rozmístění pokrývající všechny cestičky nemá menší cenu.

Lehčí variantaLehčí varianta (za 3 body): Vyřešte úlohu pro případ, kdy křižovatky budou tvořit jenom jednu nerozvětvenou cestu.

Řešení

Ada s Jacobem pod hávem noci úspěšně opustili tábor a vydali se na cestu. Po cestě se Ada podělila o několik základních informací.

Ada je příslušnicí tajného společenstva s názvem Podzemní bratrstvo. Není mu však oprávněna v tuto chvíli prozrazovat cokoliv o poslaní Bratrstva. Bratrstvo má po okolí rozesetu síť základen. Všechny základny jsou řízeny z Hlavního štábu, kam právě směřují.

Hlavní štáb zabírá většinu rozsáhlého jeskynního komplexu, v řeči mimozemšťanů zvaného Ĝesrít íhgis̆pop̆ k̇iĝes sda p̆kuterap̆. V posledních dnech se objevil problém, se kterým si Bratrstvo není schopno poradit. Chce proto požádat o pomoc Jacoba a využít jeho pozemských znalostí. Podrobnosti není Ada oprávněna sdělovat, žádost o pomoc chce vyslovit osobně Rada stařešinů.

Po poledni dorazili na pralesní mýtinku. Krom zpěvu ptáků neupoutalo nic Jacobovu pozornost. Ada na správném místě odhrnula listí a objevil se mřížový poklop. Poklop chránil úzký otvor, kterým se oba protáhli do jeskyně. Po průchodu takřka třísetmetrovou úzkou chodbou se objevili v ohromném dómu.

Ada pokynula hloučku mimozemšťanů, ať Jacobovi ukážou dóm. Sama zmizela v další chodbě vycházející z dómu hledajíc stařešiny. V dómu se nacházely desítky stanů, obydlí členů Bratrstva. Za stany se nacházel plácek sloužící jako shromaždiště. Zde byli každé ráno členové Bratrstva informováni o všem potřebném.

Dobrou čtvrtinu dómu zabírala mimozemská kovárna. Sestávala z asi tří výhní a dobrých dvou tuctů kovadlin. Mezi právě kovanými předměty Jacob zahlédl meč, lopatu, ba dokonce i svícen.

Jacob byl uchvácen sehraností mimozemšťanů, kladiva svými pravidelnými údery spíše než jako pracovní nástroje působila jako malý orchestr.

26-3-5 Rozvrh kovárny (11 bodů)

Kuchařková úlohaV této úloze se budete zabývat plánováním práce mimozemské kovárny vyrábějící všechny potřebné kovové nástroje.

Základny posílají kovárně své požadavky. Parametry požadavku jsou druh nástroje, priorita P a hodina H, do které je základna ochotna čekat. Než by dostala nástroj po hodině H, raději se zařídí jinak. Hodnoty P a H jsou kladná celá čísla.

Pro zjednodušení předpokládejme, že výroba jakéhokoli nástroje trvá jednu hodinu a během této doby nelze vyrábět nic jiného. Výroba začíná v hodinu 0, tedy na konci této hodiny může být vyroben první výrobek.

Na vstupu dostanete N požadavků, každý požadavek je určen dvojicí hodnot P a H. Protože výroba jakéhokoli nástroje trvá hodinu, typ nástroje se na vstupu vůbec neobjeví.

Váš algoritmus má za úkol sestavit optimální rozvrh výroby. To znamená pro každý požadavek určit hodinu, během které se požadovaný nástroj bude vyrábět, případně -1, pokud požadavek nebude splněn vůbec. Výrobek může být vyroben nejpozději v hodinu H.

Rozvrh je optimální, pokud součet priorit splněných požadavků je nejvyšší možný.

Příklad: Pro požadavky (4,4), (1,1), (2,2), (2,3), (4,4) (zadané v pořadí priorita, hodina nutného dokončení) je jednou ze správných odpovědí 3, -1, 1, 0, 2. Tedy vyrobíme předměty s celkovou prioritou 12 a druhý předmět nevyrobíme vůbec.

Řešení

Z jedné z mnoha chodeb ústících v dómu se vynořila Ada následovaná trojicí mimozemšťanů. Nebylo pochyb o tom, že se jedná o stařešiny. Podsaditý mimozemšťan se představil jako Ubu, Tajemník Bratrstva a Vrchní stařešina. Přivítal Jacoba a pozval jej do svého stanu.

Jacob byl pohoštěn dobrým jídlem a dozvěděl se, že za hodinu bude oficiálně přivítán. Po hodině zdvořilé konverzace se rozezněly fanfáry. Když vyšli z Ubuova stanu, na shromaždišti už postávaly hloučky mimozemšťanů.

Ubu před davem představil Jacoba a oznámil, že Jacobovi bude jako výraz úcty Bratrstva předán dar. Asi dvacítka statných mimozemšťanů po těchto slovech donesla ohromný trezor.

Ke třem stařešinům, které už Jacob poznal, se přidalo dalších devět. Všichni stařešinové se shromáždili u trezoru.

Ke zdárnému otevření trezoru bylo nutno podniknout sérii přesně daných kroků. Nejprve bylo nutno ovládací páku přepnout do spodní polohy. Čtveřice mimozemšťanů poté asi minutu točila obrovitou klikou.

Trezor

Stařešinové přistoupili k trezoru a každý vložil svůj klíč do otvoru v trezoru. Páka byla přepnuta do své horní polohy a čtveřice mimozemšťanů točila další dvě minuty klikou. Ozvalo se cvaknutí.

Další čtveřice mimozemšťanů otevřela těžké víko trezoru.

26-3-6 Trezor (8 bodů)

V této úloze budeme zkoumat mimozemský trezor. K otevření trezoru je potřeba do některých otvorů z vnějšku trezoru vložit sadu klíčů. Pokud je sada klíčů správná (správných sad může existovat více), trezor se po dostatečně dlouhém točení klikou otevře.

Princip trezoru tkví v tom, že všechny klíče odpovídají mocninám dvojky. Trezor má navíc ve svých útrobách skrytou druhou sadu klíčů. (Tvůrce trezorů totiž vyrábí všechny trezory stejně a až podle potřeb kupce navolí tyto vnitřní klíče.)

Během otáčení kliky vnitřní mechanická sčítačka sečte dohromady všechny klíče, jak vnitřní, tak ty zasunuté zvnějšku.

Je-li výsledný součet při zápisu v dvojkové soustavě tvořen samými jedničkami (na úvodní nuly se ohled nebere), trezor se otevře.

Vaším úkolem je pro zadanou N-tici vnitřních klíčů určit nejmenší počet vnějších klíčů potřebných k otevření trezoru. Klíče jsou zadány exponenty a nemusí být různé.

Poznámka: Možná jste se ještě nezabývali výpočetními modely a otázkou toho, o kterých operacích můžete prohlásit, že proběhnou v konstantním čase. Pak by vás mohlo napadnout umocnit dvojku na zadané exponenty a dále s nimi počítat. Vězte však, že výpočetní model, ve kterém bychom mohli v konstantním čase provádět aritmetiku nad libovolně velkými čísly, by byl absurdně silný.

Takový model by už neměl mnoho společného s tím, jak lze využívat skutečné počítače. Nejčastěji se proto uvažují modely, ve kterých lze v konstantním čase počítat pouze s čísly, která jsou polynomiálně velká vzhledem ke vstupním číslům. Takový model uvažujte i při řešení této úlohy.

Příklad: Pro seznam exponentů 0 1 0 1 0 2 4 4 lze trezor otevřít třeba pomocí pětice klíčů 21, 21, 23, 23 a 26.

To však není správná odpověď. Když použijeme pouze klíče o hodnotách 22 a 24, bude součet hodnot všech klíčů 63. To je ve dvojkovém zápise číslo 111111 a trezor se také otevře. Použít pouze jeden klíč pro zadaný příklad již nepostačuje.

Lehčí variantaLehčí varianta (za 2 body): Vyřešte úlohu pro případ, kdy všechny exponenty vnitřních klíčů budou různé.

Řešení

Ubu z trezoru vytáhl meč, došel k Jacobovi, poklekl a v natažených rukou mu nabídl tento dar. Za potlesku davu se stal Jacob majitelem mimozemského meče.

Po ceremoniálu se Jacob, tentokrát společně se všemi stařešiny, přesunul zpátky do Ubuova stanu. Ubu Jacobovi stručně povyprávěl o historii meče. Pak najednou zvážněl. Všichni stařešinové si sesedli blíž k Jacobovi. Zjevně nadešel čas poodhalit Jacobovi účel zdejší návštěvy.

„Drahý příteli,“ začal svou řeč Ubu, „skutečnost je prostá. Bratrstvu hrozí zkáza. Během posledního týdne se začal probouzet vulkán nedaleko Hlavního štábu. Pokud se potvrdí nejhrozivější obavy našich šamanů, láva z vulkánu zaplaví tento jeskynní systém. Nemáme dostatek jiných jeskyní, kam bychom přesunuli všechen náš lid, a na povrchu by jej stihla zkáza. Žádáme tě jménem celého našeho lidu o pomoc.“

„Drazí přátelé,“ volil Jacob opatrně svá slova. „Učiním vše, co bude v mých silách. Obávám se však, že toho nebude mnoho. Má loď ztroskotala a nezdá se, že by jakákoli technologie z ní byla použitelná. Rád bych se však na onen vulkán alespoň podíval.“

„Dobrá,“ odvětil trochu zklamaně Ubu a na chvíli se zamyslel. „Vyšlu s tebou své nejlepší lidi, budou ti ve všem nápomocni.“

O pár hodin později stál Jacob spolu s Adou a dalšími čtyřmi mimozemšťany u úpatí sopky. Z jejího vrcholku pomalu stoupaly malé obláčky dýmu.

Jacob se zamyslel. Co od něj Bratrstvo vůbec očekává? Jistě, na Zemi dávno existovala technologie, která by se s touto hrozbou vypořádala. Co si však lze počít zde? Zdálo se, že sopka lehce smete Bratrstvo. Neměl pocit, že by si to nechala jen tak vymluvit…

26-3-7 Sopečné pokrytí (12 bodů)

Praktická CodExová úlohaPro zabezpečení sopky je na Zemi nutno podniknout dvě opatření – zahájit odčerpávání lávy ze sopouchu speciálním potrubím a pokrýt ústí sopky panely tak, aby neunikal sopečný popel ani gejzíry lávy. Vaším úkolem bude nalézt optimální pokrytí.

Okolí sopky si můžeme představit jako čtvercovou síť velikosti R×S. Na každém políčku se nachází buď znak Z, nebo K. Pomocí Z je označena zem, kterou není potřeba pokrývat, naopak znaky K označují oblast sopečného kráteru, kterou je nutno pokrýt. Oblast kráteru je souvislá.

V celé úloze budeme za sousední políčka považovat ta, která se dotýkají celými stranami. Souvislou oblastí pak rozumíme množinu políček takovou, že kdykoli máme políčka A, B z této oblasti, existuje posloupnost políček z této oblasti s následujícími vlastnostmi: prvním políčkem je A, posledním B a pro každé políčko (mimo posledního) platí, že následující políčko je jeho sousedem.

Pokrývá se panely obdélníkového tvaru rozměrů ρ×σ. Pro zjednodušení úlohy budeme předpokládat, že panel lze položit pouze tak, aby pokryl obdélníkovou podoblast čtvercové sítě o ρ řádcích a σ sloupcích.

Aby celé pokrytí fungovalo, musí panely do sebe zapadnout. To znamená, že pokud spolu dva panely sousedí nějakými políčky, pak spolu musí sousedit celými svými stranami. Panely mohou sahat i za hranice původní mapy.

Nalezněte panelové pokrytí, které pokryje všechna políčka se znakem K a využije k tomu nejmenší možný počet panelů.

Příklad: Na obrázku níže vidíte jedno z možných pokrytí kráterů vlevo pomocí panelů o rozměrech 2×3.

Obrázek k 26-3-7: pokrytí kráteru

Tato úloha je praktická a řeší se ve vyhodnocovacím systému CodEx. Přesný formát vstupu a výstupu, povolené jazyky a další technické informace jsou uvedeny v CodExu přímo u úlohy.

Řešení

Nezdálo se však, že by podobná technologie byla k dispozici zde. Jak si vlastně lidstvo umělo poradit se sopkami v dobách, kdy ještě neexistovaly materiály dost odolné k jejich usměrnění? Přeci by jim neustupovalo…

Z úvah Jacoba vytrhlo zapraskání. Znělo to skoro, jako by se sopka po probuzení potřebovala nejprve protáhnout. Po dalších dvou zapraskáních nastalo opět ticho. Nemělo však dlouhého trvání, bylo po chvilce proříznuto ránou tak ohromnou, že si všichni instinktivně zacpali uši. Ze sopky se vyvalil oblak popela.

Šedivé kousky popela zvolna jako sníh dopadaly na Jacoba a mimozemšťany. Všichni stáli na místě jako přikovaní. Nikdo nebyl schopen slova. Začaly se objevovat první gejzíry lávy. První se vzpamatoval Jacob a zavelel všem k útěku.

Ozval se další výbuch. Tentokrát se už nejednalo o pouhý gejzír. Zformoval se celý proud lávy, který si jako horská bystřina razil svou cestou krajinou. Zřejmě se vydal stíhat prchající skupinku. Jacob se ohlédl a odhodil svůj batoh. Pochopil, že bude muset být opravdu rychlý.

Pokračování příště…

O Jacobových setkáních s mimozemšťany vyprávěl

Lukáš Folwarczný

26-3-8 Zdivočelá počítadla (15 bodů)

SeriálSeriál o výpočetních modelech pokračuje, tentokrát ve znamení minimalismu. V tomto dílu si ukážeme jeden z vůbec nejjednodušších teoretických strojů. Takové obyčejné kuličkové počítadlo, jen trochu programovatelné. Proto mu budeme říkat počítadlový stroj.

Definice stroje

Počítadlový stroj pracuje výhradně s přirozenými čísly. Ta mohou být libovolně velká a zahrnujeme mezi ně i nulu. Obvykle jim budeme říkat prostě čísla.

Stroj je vybaven libovolným konečným počtem registrů. Registry jsou očíslovány a každý z nich obsahuje jedno číslo.

Program stroje je tvořen konečnou posloupností instrukcí. Těch jsou k dispozici 3 druhy:

Na počátku výpočtu je ve smluvených registrech vstup a ostatní registry obsahují nuly. Instrukce se vykonávají jedna po druhé, počínaje první instrukcí programu. Pouze instrukce skoku může způsobit, že se místo následující instrukce začne provádět nějaká jiná, od níž program opět pokračuje sekvenčně.

Pokud se ocitneme mimo program (ať už tím, že jsme tam skočili, nebo po provedení poslední instrukce programu), stroj se zastaví a ve smluvených registrech najdeme výstup.

Časovou složitost bychom mohli zavést jako počet provedených instrukcí, paměťovou třeba jako velikost čísel, která se během výpočtu vyskytnou v registrech. U úloh v této sérii se nicméně nebudeme počítání složitosti věnovat, bude nás zajímat pouze počet použitých registrů. Ten se jako míra složitosti nechová, protože nezávisí na vstupu – je to spíš míra komplikovanosti programu.

Rozšíření instrukční sady

Instrukční sada našeho stroje je značně spartánská. Proto ji rovnou rozšíříme o několik zkratek pro běžné programátorské obraty.

Úkol 1 [3b]

Navrhněte následující zkratky:

Zase ty závorky

Nemůžeme opomenout naši tradiční úlohu o závorkování. Potřebujeme ovšem vymyslet, jak řetězec závorek popsat číslem. Zakódujeme ho velice jednoduše: každou levou závorku v řetězci přepíšeme na číslici 1, každou pravou na 2 a výsledek přečteme jako číslo v desítkové soustavě.

Například řetězec ()(()) přeložíme na číslo 121122, prázdný řetězec zakódujeme jako nulu.

Úkol 2 [4b]

Napište program pro počítadlový stroj, který v registru x dostane kód posloupnosti závorek a až doběhne, sdělí v registru y, zda posloupnost byla (y=1) nebo nebyla (y=0) správně uzávorkovaná.

V programu můžete používat všechny zkratky, které jsme definovali, nebo které jste vymysleli v předchozím úkolu.

O síle počítadel

Jak je vidět z předchozího příkladu, pomocí počítadlového stroje lze odpovídat na netriviální otázky. Ukážeme, že je dokonce stejně silný jako Turingův stroj (a tím pádem i jako přepisovací programy z předchozí série).

Simulace počítadel na Turingově stroji je triviální – stačí každému počítadlu vyhradit jednu pásku stroje.

Úkol 3 [3b]

Vymyslete opačný převod: popište, jak k libovolnému Turingovu stroji sestrojit počítadlový stroj, který spočítá totéž. Zvolte vhodné kódování vstupu a výstupu Turingova stroje čísly.

Nabízí se také otázka, kolik počítadel doopravdy potřebujeme. U Turingova stroje víme, že si (za cenu zpomalení výpočtu) vystačí s jedinou páskou. Jak je to zde? Stačí pevný počet počítadel? A potřebujeme vůbec tolik instrukcí?

Úkol 4 [3b]

Pro co nejmenší konstantu k dokažte, že ke každému počítadlovému stroji existuje ekvivalentní stroj, který použije jen k registrů. Můžete předpokládat, že původní stroj pro vstup i výstup využívá jediný registr x. Dokázali byste k ještě snížit, pokud byste mohli zavést nějaké vlastní kódování vstupu?

Úkol 5 [2b]

Navrhněte ještě menší instrukční sadu, pomocí které půjdou vyjádřit všechny tři instrukce našeho počítadlového stroje. (Nová sada nemusí nutně být podmnožinou té původní.)

Martin „Medvěd“ Mareš

Hroší čajovna

Řešení