Pátá série dvacátého šestého ročníku KSP
Celý leták v PDF.
I v této sérii můžete získat sladkou odměnu! Čokoládu pošleme každému,
který z úloh této série získá dohromady alespoň 50 bodů.
Zadání úloh
V minulém díle se Jacob, zkoušený osudem již pádem hvězdné lodě, setkáním
s mimozemšťany i výbuchem sopky, propadl do nějaké podzemní prostory. Teď
v úžasu zíral na kovovou bednu se začouzeným nápisem „Made in China“.
Tohle je přeci lidská technika! A určitě to nejsou jen náhodně popadané
trosky z Freyi, protože tady je to celé propojené. To
znamená… „Jsi v pořádku?“ přerušil náhle jeho myšlenky hlas shora.
Jacob vzhlédl a spatřil jednoho mimozemšťana, jak klečí na okraji díry,
kterou sem propadl.
Ubu ho asi poslal, aby na něj dával pozor. No teď se to hodí, pomyslel si Jacob.
Poslal mimozemšťana pro posily a za půl hodiny už táhli největší
z kovových beden do tábora.
Jacob chtěl přijít na to, k čemu zařízení slouží. Jelikož bylo, zdá se, vyrobeno
jako co nejlevnější a nejuniverzálněji použitelné zařízení, skládalo se jen
z univerzální řídící jednotky, která byla naprogramována pomocí spousty relátek
uspořádaných v pravidelné mřížce. Bohužel některá z nich byla spálená a bylo
nutné je vyměnit.
26-5-1 Made in China (9 bodů)
 Jacob má před sebou podivné zařízení a chtěl by ho spustit. Jenže předtím musí
vyměnit několik spálených relé. Každé relé má své typové označení (přirozené
číslo), které jde poznat po vyndání relé ze zařízení. Avšak spálená relé mají
označení bohužel spečená k nepoznání.
Jacob má před sebou podivné zařízení a chtěl by ho spustit. Jenže předtím musí
vyměnit několik spálených relé. Každé relé má své typové označení (přirozené
číslo), které jde poznat po vyndání relé ze zařízení. Avšak spálená relé mají
označení bohužel spečená k nepoznání.
Podle schématu na zařízení víme, že původně byla relé
uspořádaná podle tabulky, kde v horní řádce i na levém okraji této tabulky
byla relé označená postupně rostoucími přirozenými čísly začínajícími nulou
(0, 1, 2, 3, …).
Zbytek tabulky byl vyplněn tak, že na pozici [A,B] se nacházelo relé
s nejmenším takovým číslem, které se doposud doleva ani nahoru od něj nevyskytlo
(všechny tyto pozice již samozřejmě musí být osazeny). Prvních šest řádků
a sloupců této tabulky tak bude vypadat takto:
0 1 2 3 4 5
1 0 3 2 5 4
2 3 0 1 6 7
3 2 1 0 7 6
4 5 6 7 0 1
5 4 7 6 1 0
Jacob potřebuje vyměnit několik spálených relé, ale nechce se mu kvůli tomu
zkoumat všechna relé doleva a nahoru od těchto pozic. Proto by od vás potřeboval
postup, který by mu rychle řekl, jaké relé má umístit na pozici [A,B].
Řešení
Po osazení všech relé se zařízení spustilo a zobrazilo na malé obrazovce několik
informací. Po zběžném pročtení bylo Jacobovi vše jasné. Za pár minut už Ubu
a několik dalších starších seděli v jednom ze stanů.
„Ctihodný Ubu, viděl někdy někdo z vašich lidí přímo někoho z vládnoucí
kasty?“ zeptal se rovnou.
„Ne, podle našich zvědů nikdy nesundávají své blyštivé helmy, Jacobe.“
Jacob se nadechl, tohle by mohlo být ošemetné: „Ctihodný Ubu, rado starších,
věc, kterou jsem vykopal, pravděpodobně spustila výbuch sopky. Je to asi
nástroj, který sem umístil někdo z vládcových lidí. Ten nástroj ale poznávám,“
nadechl se, „je to technika mých lidí, nebešťanů.“
Viděl, jaké reakce to mezi radou starších vyvolalo, a tak rychle pokračoval:
„O těch lidech nic nevím, možná to bude nějaký odštěpený klan. Musím se ale
vypravit do královského města a promluvit si s nimi, přesvědčit je o tom, že
dělají špatnou věc.“
Ještě chvíli diskutoval s radou, než se mu ji povedlo přesvědčit, že ho mají
nechat jít samotného. Přízvuk už měl docela dobrý, tak dostal alespoň místní
ekvivalent kutny, kterou tu občas nosili starší mimozemšťané a která mu
zakrývala obličej i celé tělo. S ní by snad mohl splynout s místními. Mimo to si
ještě vzal meč, který získal při rituálu, a dostal od Ady docela přesnou mapu
pralesa. Rozloučil se s místními, minul místní ekvivalent kočky ležící na kraji
tábora a vyrazil.
Jako první se vydal k vraku Freyi. Tam si cestu pamatoval, a tak si během
ní plánoval trasu od vraku směrem ke královskému městu. Bude to dlouhá cesta,
vedoucí v první části skrz hustý prales, kde bude muset dávat pozor,
aby v něm nepřehlédl žádnou odbočku.
26-5-2 Cesta pralesem (9 bodů)
Prales je místo, kde se velmi lehce přehlédne pokračování cesty. Máme mapu
pralesa představovanou čtvercovou mřížkou o rozměrech R × S políček,
dále máme zadané startovní políčko a cílové políčko.
Pohybovat se v mapě můžeme jen horizontálně nebo vertikálně, šikmo ne. Každé
políčko má navíc dva koeficienty přehlédnutelnosti. Jeden pro cestu vedoucí
přes něj rovně (shora dolů, zleva doprava nebo naopak) a druhý pro odbočení
(tedy všechny zbylé průchody – zleva dolů, shora doleva, …).
Protože chceme mít co největší naději, že se v pralese neztratíme, je vaším
úkolem nalézt cestu ze startovního do cílového políčka, která bude mít v součtu
přes všechna políčka cesty co nejmenší přehlédnutelnost (přehlédnutelnost ve
startovním a cílovém políčku neuvažujte).
Řešení
Než si Jacob naplánoval celou další cestu, už stál u boku UFC Freya. Torzo
lodě i po těch letech stále vypadalo majestátně, ale brázda v pralese
i poničené okolí po nouzovém přistání už pomalu zarůstaly novou vegetací.
Během svého několikaletého pobytu v mimozemském táboře se do vraku párkrát
podíval, ale vždy se vydal jen k výstrojnímu skladu pro nové boty. Od
ztroskotání nikdy nezašel dál, to místo na něj z nějakého důvodu působilo
tísnivě a stejně tam nebylo nic zajímavého – nouzový signál nešel vyslat kvůli
nějakému rušení v atmosféře a vody i jídla měl od mimozemšťanů dost.
Teď se skrz zprohýbaný koridor prodral hlouběji do lodi. Freya jako
původně válečná transportní loď měla v přídi několik zabezpečených skladů
a Jacob je chtěl zkontrolovat. Zastavil se u zavřené přepážky, která nesla stopy
po použití malého plazmového hořáku – někdo se chtěl propálit skrz, ale malým
hořákem se mu to zdá se nepovedlo. To znamená, že se tady objevil nějaký jiný
člověk, pravděpodobně někdo z těch, kteří teď vládnou domorodcům.
Jacob odklopil ovládací panel a několika stisky probudil palubní počítač z jeho
spánku. Chvíli trvalo, než naběhl, ale záložní baterie stále poskytovaly
dostatek energie. Potom, co Jacob zadal svůj přístupový kód, se ale nic nestalo.
Zkusil to znovu, a teprve pak si všiml, jakou paseku na kabelech neznámý
návštěvník s plazmovým hořákem provedl. Ještě že ve skladu údržby byla celá
krabice náhradních – jen rychle najít ten správný.
26-5-3 Náhradní kabel (10 bodů)
 Máme před sebou bednu plnou náhradních kabelů a potřebujeme rychle poznat,
jestli jsou nějaké dva kabely stejné. Nejsou to ale jen kabely se dvěma konci,
tyto jsou rozvětvené a mohou obecně propojovat i více věcí dohromady.
Máme před sebou bednu plnou náhradních kabelů a potřebujeme rychle poznat,
jestli jsou nějaké dva kabely stejné. Nejsou to ale jen kabely se dvěma konci,
tyto jsou rozvětvené a mohou obecně propojovat i více věcí dohromady.
Každý kabel si tedy můžeme představit jako spoustu uzlů pospojovaných
jednotlivými dráty. Celý kabel je navíc pospojovaný tak, že v něm neexistují
cykly – z každého uzlu do každého jiného se lze dostat jen jedinou cestou.
Informatik by tedy takovýto rozvětvený kabel mohl nazvat stromem.
Jacob vždy náhodně uchopí dva kabely, a to tak, že je chytí za nějaký uzel
a zbytek nechá viset dolů. Tomuto uzlu budeme říkat kořen. Díky tomu, že
kabely jsou v uzlech spojeny v pevném pořadí, můžeme lehce popsat zbytek
kabelu například tak, že kořen označíme indexem 0 a zbylé uzly vyjádříme jako
N čísel označujících, pod kterým jiným uzlem je připojený i-tý uzel.
V případě více uzlů připojených pod ten samý je uvedeme třeba v pořadí proti
směru hodinových ručiček (rozmyslete si, že je jedno, od jaké pozice začneme
připojené uzly popisovat, když dodržíme jejich pořadí).
Jacoba by nyní zajímalo, jestli náhodou nejsou dva kabely, které drží v ruce,
stejné. To znamená, že kdyby si je chytl oba za správný uzel, vypadaly by pak
oba stejně (mimo přechycení za jiný uzel nesmíme pořadím kabelů v jednotlivých
uzlech nijak rotovat).
Příklad: Pro kabely níže stačí, abychom prostřední kabel chytili za uzel
s indexem 1 a správně otočili, pak budou levý a prostřední kabel stejné
(všimněte si, že uzel 2 se sice zrotoval na druhou stranu, ale pořadí uzlů
připojených k uzlu 1 se tím nijak nezměnilo). Nicméně pravý kabel se od nich
liší (má jiné pořadí podstromů v uzlech).
Levý Prostřední Pravý
kabel kabel kabel
1: 0 1: 0 1: 0
2: 1 2: 1 2: 0
3: 1 3: 1 3: 2
4: 0 4: 3 4: 3
5: 4 5: 3 5: 3
6: 0 6: 0 6: 2
Řešení
Po zapojení správného kabelu zadal Jacob znovu svůj přístupový kód. Panel
zezelenal a s hrozivým skřípotem se pancéřová přepážka otevřela asi do poloviny.
Jacob prolezl skrz a ocitl se v sekci lodě, ve které od startu nebyl. Matně si
pamatoval, že sem nakládali nějaké záhadné bedny s tajným obsahem – stále zde
stály a vypadalo to, že jim nouzové přistání ani příliš neublížilo.
Jacoba ale zajímalo něco jiného. V malém skladu na konci oddělení se nalézala
bedna, o níž vědělo jen několik členů bývalé posádky. Pomalu ji otevřel a vytáhl
pár věcí ven. Pak zvedl plazmovou karabinu, zapřel si ji o rameno a pohledem
skrz zaměřovač vyzkoušel, že vojenská zbraň stále funguje. Myslí mu proletěly
vzpomínky na válku… jeho služba u elitní roty mariňáků, kamarádi v jednotce
a jejich heslo Semper Fidelis – vždy věrní.
Zatřepal hlavou a zahnal vzpomínky. Je to už skoro dvacet let, co po konci války
opustil armádu. Schoval masivní zbraň do batohu, sundal z helmy noční vidění
a termovizi, k boku si připnul malou pistoli na uspávací šipky a pobral ještě
několik drobností včetně sady nářadí. Pak vyrazil.
Podle mapy odhadl, že královské město bude ležet něco přes pět set kilometrů od
místa, kde havaroval. Během svého putování minul několik mimozemských osad, ale
vždy se držel mimo ně. Patnáctý den cesty, odhadem půlden cesty od královského
města, mu však už došlo všechno jídlo. Chtěl si před setkáním raději pořádně
odpočinout, a tak se rozhodl, že navštíví nejbližší vesnici, na kterou narazí.
Jednu takovou objevil k večeru. Asi hodinu ji pozoroval, než se odvážil ukázat
se. Zdálo se, že místní náčelník zrovna řešil nějaký problém s rozdělováním
surovin na výrobu jídla.
26-5-4 Rozdělování jídla (11 bodů)
 Vesnický náčelník má k dispozici K typů různých surovin a chce je co nejlépe
využít, aby mu jich dohromady zůstalo co nejméně nepoužitých. Od každé suroviny
má na začátku nějaké množství m1,…,mK (mi ≥ 0).
Vesnický náčelník má k dispozici K typů různých surovin a chce je co nejlépe
využít, aby mu jich dohromady zůstalo co nejméně nepoužitých. Od každé suroviny
má na začátku nějaké množství m1,…,mK (mi ≥ 0).
Obyvatelé vesnice mu předložili N receptů. Každý recept spotřebuje nějaké
množství od každé suroviny, tedy je zadaný K čísly a1,…,aK
(ai ≥ 0) a lze ho použít maximálně jednou (a to jen tehdy, pokud ještě
od každé suroviny zbývá alespoň tolik, kolik recept spotřebuje).
Vaším úkolem je ze všech
N receptů vybrat takové, které dohromady zanechají co
nejmenší zbytek surovin (tedy pokud si zbytky označíme jako
z1,…,zK, tak
∑ zi bude co nejmenší možné).
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Potom, co se s nimi Jacob najedl, poznal podle náhrdelníku s tajným heslem
v jednom z domorodců člena Bratrstva. Počkal, než odejde stranou, a pak
se za ním nenápadně vydal.
Ve chvíli, kdy si před ním Jacob sundal z hlavy kápi, se mimozemšťan zarazil,
jako by ho někdo praštil palicí po hlavě. Pak ale jeho pohled sklouzl na
náhrdelník Bratrstva, který Jacob dostal od Ady, a došlo mu to: „Ty
jsi ten neznámý cizinec, který nám slíbil pomoc, že? Co děláš takhle daleko od
hlavního tábora? A mimochodem, já jsem Lakus.“
Jacob mu všechno vysvětlil a také mu řekl, že by se potřeboval nenápadně dostat
do královského města, aby si promluvil s králem. To, že jsou to taky pozemšťané
jako on, raději nezmiňoval.
Mimozemšťan se zamyslel a pak pravil: „Pracuji se skupinkou řemeslníků, kteří
do města dopravují kámen. Využíváme k tomu staré podzemní tunely, tudy by ses
tam mohl dostat.“
* * *
Druhý den ráno už Jacob pomáhal tlačit velký povoz kamení naložený tak, že byl
trojnásobně vyšší než on sám. Měl na sobě stále kápi, ale batoh s karabinou
a největšími věcmi dal raději Lakusovi do úschovy, nechtěl aby se případně
dostaly do rukou královým lidem.
Právě se blížili k vstupu do tunelu, město se tyčilo na ostrohu nad nimi. Jacob
si mimo jiné všiml pozemsky vyhlížející antény na největším z domů. Náhle je
zastavilo zavolání jednoho z hlídačů u ústí do tunelu. Začal se hádat s předákem
skupinky, jestli se takhle velký povoz do tunelu vejde, nebo jestli ho bude
nutné složit tady a náklad odnosit ručně.
26-5-5 Průjezd tunelem (12 bodů)
Potřebujeme zjistit, jestli náš povoz projede tunelem. Povoz má průřez
obdélníku rovnoběžného se souřadnými osami, průřez tunelu je představován
konvexním mnohoúhelníkem (zadaným na vstupu třeba jako posloupnost vrcholů po
směru hodinových ručiček).
Ptáme se, jestli se povoz vejde do tunelu, neboli jestli existuje nějaké
posunutí obdélníku takové, že se celý obdélník vejde dovnitř
konvexního mnohoúhelníku. Obdélník můžeme posouvat v libovolném směru (tedy
klidně i nahoru a dolů), ale nesmíme ho otáčet. Pokud takové posunutí existuje,
najděte ho.
Řešení
Po proniknutí do města se Jacob oddělil od skupinky mimozemšťanů. Opatrně
proklouzl okolo stráží a vyšplhal na vyvýšenou věž na okraji hradeb. Zde zalehl
a vytáhl z kapsy dalekohled.
Pozorně si prohlédl antény, které už dříve spatřil. Podle toho, kam byly
zaměřené, se pravděpodobně používaly jen k místní komunikaci. Jeho pohled
upoutala vyčnívající kovová věc za královským palácem, ale ze své současné
pozice tam neviděl. Rozhodl se počkat do noci a pak se přes střechy jednotlivých
staveb opatrně přesunout blíže paláci.
Čekání na tmu využil k tomu, že si pro každou oblast města našel nejvyšší
stavbu, kterou by při nočním přesunu mohl použít jako pozorovatelnu.
26-5-6 Nejvyšší stavby (12 bodů)
Chceme v mimozemském městě najít vždy lokálně nejvyšší stavbu. Plán mimozemského
města je tvořen čtvercovou sítí o rozměrech R × S, kde pro každé
políčko známe výšku stavby, která se na něm nalézá. Dále máme zadaná čísla
r a s (platí r ≤ R a s ≤ S) – velikost oblasti, která nás zajímá.
Chtěli bychom pro každou oblast velikosti r × s zjistit, jakou
nejvyšší stavbu obsahuje.
Výstupem programu by tedy měla být tabulka velikosti
(R - r + 1) × (S - s + 1), kde políčko [i,j] bude obsahovat maximální
výšku stavby nalézající se v oblasti velikosti r × s s levým vrchním
rohem v tomto políčku.
Ukázkový vstup:
r = 3, s = 3
1 4 2 2 0 2
0 2 2 2 1 1
2 1 3 3 0 1
8 1 0 5 0 6
Ukázkový výstup:
4 4 3 3
8 5 5 6
 Lehčí varianta (za 6 bodů): Vyřešte úlohu jen pro jednorozměrný případ (tedy R=r=1).
Lehčí varianta (za 6 bodů): Vyřešte úlohu jen pro jednorozměrný případ (tedy R=r=1).
Řešení
Padla noc. Jacob se plížil po střechách jen v černé kombinéze, pomáhaje si
nočním viděním. Díky tomu, že si přesně zmapoval nejvyšší budovy ve městě, se
dokázal snadno vyhýbat hlídkám. Metr po metru se blížil ke královskému paláci.
Seskočil z poslední střechy, obešel věžičku a naskytl se mu pohled na něco
podivného. Samozřejmě tu věc poznával, za svoji kariéru ji viděl mnohokrát na
spoustě hvězdných lodí. Nebo alespoň její modernější sourozence, tohle byl vážně
starý model, ten už se skoro půlstoletí nepoužíval.
Co ho ale zaskočilo mnohem víc než shledání se starým záchranným raketoplánem
Mark II, bylo to, že aktuálně vypadal jako vyvržený vorvaň. Jeho motory to asi
odnesly při tvrdém přistání, aspoň podle škod na zádi. Plátování z celého okolí
fúzního reaktoru bylo odstraněno a od odhalených součástek vedlo směrem do
paláce několik tlustých svazků kabelů.
Další vedly z místa bývalého kokpitu a končily u soustavy antén na střeše vlevo
od něj. Působilo to celé, jako kdyby se někdo rozhodl využít z raketoplánu
každou použitelnou věc, začal ho přestavovat na obytný přívěs křížený s továrnou
na boty a v půlce navíc ztratil výrobní plány.
Náhle ho vyrušil šoupavý zvuk po jeho pravici. Rychle vyskočil, otočil se a ztuhnul
s rukou na šipkové pistoli. Z půl metru hleděl do zrcadlového hledí skafandru.
Kriticky si uvědomil, že ho ten člověk má špatně nasazený, zámky helmy nebyly
zacvaklé a navíc na sobě neměl rukavice. To mu však nijak nezabránilo v tom
praštit Jacoba po hlavě kovovou tyčí.
* * *
Probudil se v temné místnosti a příšerně ho bolela hlava. Zahlédl vedle sebe
nějakého člověka. Poprvé po pěti letech zase spatřil příslušníka lidské rasy!
„Omlouvám se za tu ránu na hlavě, můj syn je trochu zbrklý,“ začal člověk
starým hlasem. „To víte, nespatřil nikdy nikoho jiného mimo nás, narodil se
pět let po ztroskotání.“
„Jak jste tu dlouho?“ zeptal se Jacob a mnul si bouli na hlavě.
„Naše loď, Hermes, tu ztroskotala před asi 30 pozemskými roky, pokud
počítám správně. Já jsem Cedric, nejvyšší přeživší důstojník,“ řekl stařec,
„kapitán a většina ostatních důstojníků zemřeli, když naváděli loď někam do
nejhlubšího moře…selhával nám reaktor a oni nechtěli zamořit místní
ekosystém výbuchem.“
Hermes, to mu něco říkalo. Nebyla to ta civilní loď, která se ztratila
během války? Původně se myslelo, že byla v nějaké potyčce omylem zničena, ale
průzkum záznamů všech zúčastněných stran neukázal nic.
„A od té doby tu využíváte domorodce?“ přešel Jacob hned k jádru věci.
„Oni si myslí, že jsme bohové. A já nemám v úmyslu jim to vyvracet. Sem tam
se sice objeví nějaký pochybovač, ale jak se říká, dostatečně pokročilou
technologii nelze odlišit od magie – ty blázni se daj hrozně snadno
přesvědčit. A když to nejde…“ s těmi slovy si nadhodil v ruce původně
Jacobovu šipkovou pistoli.
„Ty jsi tu spadl s tou velkou lodí před pár lety, ne? Pokoušeli jsme se do ní
dostat, ale s našimi nástroji ze záchranného člunu jsme se nedokázali proříznout
ani přes jednu přepážku. Ty ale určitě máš přístupové kódy, že?“
„Předpokládáte, že vám pomůžu?!?“ zeptal se Jacob.
„Ty se nechceš nechat považovat těmihle tupci za boha?“ podíval se Cedric na
Jacobův znechucený výraz. „No dobrá, pár dnů na přemýšlení možná změní tvůj
názor.“
S těmito slovy odešel a nechal Jacoba samotného v cele. S vyhlídkou na dlouhý
pobyt začal Jacob zkoumat své vězení. Na jedné zdi objevil dlouhý zápis jedné
z oblíbených mimozemských her, asi si tu nějaký vězeň taky krátil dlouhé čekání.
Hra se docela podobala pozemským piškvorkám a Jacoba by zajímalo, jak vlastně
dopadla.
26-5-7 Partie piškvorek (13 bodů)
Jacob našel zápis jedné partie mimozemských piškvorek, která se hraje se na
čtvercové síti o rozměrech N × N. Zápis hry je tvořen třemi typy tahů:
- Na políčko [A,B] umísti kolečko
- Na políčko [A,B] umísti křížek
- Vymaž znak z políčka [A,B]
Po každém tahu by nás zajímalo, jak je dlouhá aktuálně nejdelší souvislá řada
symbolů (v řádce, sloupci nebo na úhlopříčce). Vybudujte datovou strukturu
držící aktuální stav hrací desky, která by navíc měla zvládat rychle zapisovat
jednotlivé tahy a po každém tahu rychle vypsat aktuálně nejdelší řadu.
Předpokládejte, že tahů bude řádově stejně, jako je velikost hrací desky (tedy
řádově N2). Tahy budou vždy korektní, tedy nebude docházet k mazání prázdného
políčka ani k umisťování znaku na neprázdné políčko.
 Lehčí varianta (za 5 bodů): Vyřešte úlohu pro partii, v níž se znaky nebudou mazat
(nastanou jen tahy prvních dvou typů).
Lehčí varianta (za 5 bodů): Vyřešte úlohu pro partii, v níž se znaky nebudou mazat
(nastanou jen tahy prvních dvou typů).
Řešení
Po zamotání se v partii piškvorek Jacob ulehl na tvrdou zem – ráno moudřejší
večera, pomyslel si. Uprostřed noci ho ale probudil slabý hlas. Chvíli přemýšlel,
jestli se mu to nezdálo, ale když Adu zaslechl znova, okamžitě vyskočil. Dívala
se na něj skrz malé okénko a podávala mu jeho plný batoh.
Bez rozmýšlení ho popadl, vyndal z něj plazmovou karabinu, připjal si meč k boku
a řekl Adě: „Radši ustup.“ Pozvedl zbraň, zacílil a několika přesnými
výstřely zničil mříž. Pak se vzniklým otvorem protáhl k Adě. „Jak…“ začal,
ale Ada ho umlčela. Ukázala mu rukou a rozeběhla se do temnoty.
Nedostali se ale daleko. Na nádvoří, kus od raketoplánu, je obklíčili strážci
s ostrými oštěpy. „Já je nechci zranit, Ado,“ sykl, „není tu nějaká jiná
cesta?“
„Máš meč? Vytáhni ho, dělej!“ řekla rychle Ada.
Jacob si spustil karabinu na popruhu dolů a tasil meč. Co se stalo dál, nechápal.
Strážní upřeli pohled na blyštivou čepel zdobenou kameny, začali si něco mumlat
a ustupovali. Zaslechl něco o proroctví a prorokovi. Co ho ale udivilo víc, bylo
to, že jeden z kamenů na meči začal v blízkosti fúzního reaktoru raketoplánu
nezvykle pulzovat. Vrhl rychlý pohled do změti kabelů a pak mu to došlo.
„Ado, chyť ten meč a drž je od nás dál!“
Ada opatrně uchopila meč, jako by se bála, že se o něj spálí. Jacob začal
kuchat obnažené zařízení, než se mu povedlo uvolnit vlnový rezonátor montovaný
na tyto staré reaktory. Okamžitě se spustil nouzový protokol a reaktor se
odstavil, palác náhle potemněl.
Ada s Jacobem využili nastalý zmatek a rychle unikli z města. Tam na ně čekalo
pár dalších členů Bratrstva s tvory vzdáleně podobnými koňům. Cesta nazpět
k Freye jim nezabrala ani tři dny.
Během zastávek vyrazil Jacob z meče, ke zděšení ostatních, několik kamenů a něco
s nimi a s ukradeným rezonátorem dělal. Co, to nechtěl říct, ale naléhal, že jako
první musí k vraku lodě. Také se cestou věnoval sepisování nějakých věcí do
elektronického zápisníku.
Když tam dorazili, vylezl po trupu nahoru až k troskám anténního pole. Vůbec
neočekával, že by se na téhle planetě mohlo vyskytovat thallium v krystalické
podobě. Pokud tohle vyjde, mohl by přes něj pomocí toho prastarého rezonátoru
vyslat krátký subprostorový impulz, který by mohl proniknout vším tím rušením
okolo.
Potom, co všechno správně pospojoval, usedl k jednomu z řídících panelů. Přehrál
do paměti lodního počítače připravenou zprávu z elektronického zápisníku.
Zhluboka se nadechl a potvrdil příkaz. Lodní počítač ve zlomku sekundy přetížil
anténní systém a v efektním záblesku spálil krystal na prach…
* * *
Ve sledovacím centru vesmírného provozu na Zemi zrovna Bob pojídal sendvič, když
vtom začal jeho počítač varovně pípat. Líně zamáčkl spínač poplachu a podíval se, co
za planý poplach to je teď. Sendvič mu vypadl z ruky a o sekundu později sahal
po interkomu: „Šéfe…Ano, vím, že jsou dvě v noci, ale tohle musíte vidět!“
Pokračování příběhu na podzimním soustředění…
Další část příběhu o Jacobovi pro vás sepsal
Jirka Setnička
26-5-8 Automatizovaný graf (15 bodů)
 Ve všech čtyřech minulých dílech tohoto seriálu jsme se potulovali po pomyslné
zoo výpočetních modelů a zastavovali se u zajímavých exemplářů. Dnes naši
letošní pouť zakončíme u jednoho podivného výběhu, ve kterém se nepase
jedno velké výpočetní zvířátko, ale spousta maličkých. Řeč bude o grafových automatech.
Ve všech čtyřech minulých dílech tohoto seriálu jsme se potulovali po pomyslné
zoo výpočetních modelů a zastavovali se u zajímavých exemplářů. Dnes naši
letošní pouť zakončíme u jednoho podivného výběhu, ve kterém se nepase
jedno velké výpočetní zvířátko, ale spousta maličkých. Řeč bude o grafových automatech.
Úvod
Grafový automat se skládá ze spousty stejných jednoduchých automatů
(můžeme si je představit třeba jako malé programy, omezení viz níže), které jsou
nějakým způsobem pospojovány a společně řeší nějaký složitější problém. Abychom
si nepletli pojmy, budeme dále grafovému automatu jako celku říkat
grafomat a pojmem automat budeme označovat jednotlivé malé automaty
obsažené v grafomatu.
Řečeno formálně, grafomat si můžeme představit jako obyčejný neorientovaný
graf tvořený množinou vrcholů a množinou hran mezi
nimi. V každém vrcholu sídlí jeden automat a hrany nám vyjadřují to, jak jsou
automaty mezi sebou propojené. Pro účely tohoto seriálu si dovolíme pojmy
vrchol a automat ve vrcholu zaměňovat.
Aby navíc mohl každý automat rozpoznat své sousedy, jsou v každém vrcholu
všechny hrany, které z něj vychází, očíslovány navzájem různými čísly 0,
1, 2, … Jedna hrana přitom na obou koncích může (ale nemusí) dostat
různá čísla, takže spíše než hrany číslujeme konce hran. Pokud budeme
mluvit o nějaké hraně z pohledu určitého automatu, budeme její konce nazývat
místní a protější.
Navíc budeme pro jednoduchost předpokládat, že ze všech vrcholů vede
stejný počet hran. Grafům s touto vlastností se říká regulární, nebo
přesněji K-regulární, kde K je počet hran vycházejících z vrcholu.
To mimochodem znamená, že v celém grafu se nachází právě N · K/2 hran,
neboť každá hrana má 2 konce a konců napočítáme N · K.
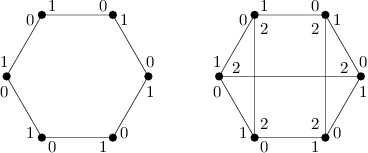
Ukázku 2-regulárního a 3-regulárního grafomatu na 6 vrcholech s očíslovanými
hranami můžete vidět níže.
Automaty a jejich paměť
Už víme, jak grafomat vypadá jako celek, ale ještě bychom si měli popsat, jak
vypadají jednotlivé automaty ve vrcholech. Jak už jsme řekli výše, všechny
automaty musí být stejné – navzájem se budou odlišovat jen tím, co který z nich
dostane na vstupu, a tím, co uvidí okolo sebe.
Formálně vzato, budou to konečné automaty, o kterých jsme psali seriál
ve 23. ročníku. Abychom je nemuseli precizně definovat, budeme si je raději
představovat jako velmi jednoduché programy. V příkladech a v řešeních budeme
programovat v Pythonu, svá řešení můžete psát ve svém oblíbeném jazyce,
pokud si myslíte, že je na to vhodný. Zavedeme ale několik omezení, aby
možnosti našich programů odpovídaly možnostem konečných automatů.
Předně omezíme paměť: Každý automat si může pamatovat jen konstantně mnoho bitů
informace nezávisle na velikosti vstupu. Můžeme použít libovolný pevný počet
proměnných nějakého libovolného, ovšem omezeného rozsahu. Smíme si například
pamatovat číslo od 0 do 42, ale nemůžeme si pořídit proměnnou, ve které bychom
si spočítali počet vrcholů grafu – taková proměnná by musela mít horní mez
závislou na velikosti vstupu, což nemáme dovoleno.
Druhé omezení vyplývá z prvního: V programech jednotlivých automatů nemůžeme
použít rekurzi a pro všechny cykly musí existovat konstantní horní mez na
počet iterací.
Zbývá určit, jak spolu mohou automaty komunikovat. Kdykoliv
jsou dva automaty propojeny hranou, vidí si navzájem do paměti. Mohou si do
ní ovšem jen nahlížet, ne ji jeden druhému přepisovat. Pro přístup k paměti
sousedů máme v každém automatu k dispozici dvě pole indexovaná místním číslem
hrany (tedy od 0 do K-1):
- P[i] obsahuje protější číslo hrany s místním číslem i.
- S[i] přistupuje k proměnným souseda připojeného hranou s místním číslem i.
Pomocí konstrukce S[i].promenna přečteme libovolnou sousedovu proměnnou.
Jen se nesmíme odkazovat na jeho pole P a S, tedy není možné se například
zeptat na proměnnou sousedova souseda.
Průběh výpočtu a jeho ukončení
Jak bylo naznačeno výše, výpočet probíhá v taktech. V každém taktu se automat
může podívat na stav proměnných svých sousedů a podle nich a svého vlastního
stavu provést nějaký výpočet a modifikovat vlastní proměnné. (Pokud během
taktu soused své proměnné změnil, stále vidíme jejich stav z počátku taktu.)
Když se automat rozhodne, že už pro něj veškerá práce skončila, může zavolat
speciální instrukci stop. Od této chvíle až do konce běhu celého grafomatu
už tento automat nevykoná žádnou akci. Jeho sousedé stále mohou číst
jeho proměnné, ale už není žádný způsob, jak by jeho výpočet mohl být opět
nastartován. Poté, co instrukci stop zavolají všechny automaty v grafu,
končí celý výpočet.
Druhou možností ukončení výpočtu je ustálení. Tím se myslí, že se dva
takty po sobě nezmění v žádném automatu hodnota jakékoliv proměnné (rozmyslete si,
proč potřebujeme dva takty a nestačí nám jeden – souvisí to s tím, že automaty
vidí stav proměnných souseda jakoby o tah nazpět).
Pokud se grafový automat nikdy celý nezastaví (ani instrukcí stop ani
ustálením), je to špatně a takový program je chybný.
Vstup je realizován tak, že se před prvním taktem výpočtu objeví ve smluvených
proměnných každého automatu vstupní hodnoty (jaké a v jakých proměnných, to záleží
na úloze). Výstup je obdobný, po konci výpočtu by se ve všech automatech měla
ve smluvených proměnných nacházet správná výstupní hodnota.
Při počítání složitosti nás bude zajímat jen počet taktů do zastavení celého
grafového automatu (na rychlosti výpočtu jednotlivých automatů ve vrcholech
nezáleží). Odhad počtu taktů stačí dělat jen asymptoticky (pomocí O-notace),
pokud to konkrétní úloha nebude vyžadovat jinak.
Příklad 1 – hledání dosažitelných vrcholů
Zadání: Mějme 5-regulární graf na N vrcholech a v každém vrcholu
proměnnou a. Na začátku bude ve všech vrcholech a=0 s jedinou výjimkou
vrcholu A, kde bude a=1. Po konci výpočtu by mělo být a=1 ve všech
vrcholech, kam lze z vrcholu A po hranách grafu dojít.
Řešení: Použijeme princip prohledávání grafu do šířky – každý vrchol bude
sledovat své sousedy a ve chvíli, kdy se v nějakém z nich objeví a=1, sám si
také své a nastaví na 1. Až se hodnoty a ustálí, výpočet se přirozeně
zastaví. Program pro jednotlivý automat bude vypadat následovně:
# Proměnné:
# a - rozsah 0..1
# i - rozsah 0..4, výchozí hodnota 0
for i in range(5):
if S[i].a == 1:
a = 1
Program vykoná nejvýše N taktů. Nejpomaleji poběží, pokud má graf tvar cesty.
Jestliže bude graf „hustší“, program může doběhnout mnohem rychleji –
například pro úplný graf vykonáme jen 3 takty: v prvním se všude
nastaví a=1 a zbylé dva slouží pro ustálení.
Příklad 2 – nalezení protějšího vrcholu
Zadání: Mějme 2-regulární graf na N vrcholech složený z jediného cyklu
sudé délky (graf je tedy sudá kružnice délky N). Na začátku je jeden vrchol
označen: má x=1, zatímco ostatní x=0. Chceme najít protější vrchol a také ho
označit (nastavit mu x=1).
Řešení: Pošleme si po kružnici signály směrem doleva i doprava a ve chvíli,
kdy se potkají, tak víme, že jsme nalezli vrchol přesně naproti. Zde pro ukázku
použijeme zastavení pomocí stop, i když by šlo napsat i verzi zastavující
ustálením.
# Proměnné:
# x - rozsah 0..1
# signal - rozsah 0..1, výchozí hodnota 0
if x == 1:
# Vyšleme úvodní signál na obě
# strany a skončíme
signal = 1
stop
if S[0].signal and S[1].signal:
# Dostali jsme signál z obou stran
x = 1
stop
elif S[0].signal or S[1].signal:
# Signál přišel alespoň z jedné strany
signal = 1
stop
Celý výpočet poběží právě N/2 taktů.
Úkoly
Úkol 1 [3b]
Mějme 2-regulární graf na N vrcholech (N je dělitelné třemi) složený z jediného
cyklu. Na začátku je jeden vrchol označený: má x=1, zatímco ostatní vrcholy mají
x=0. Vaším úkolem je označit zbylé dva vrcholy ve třetinách kružnice. Tedy
pokud si startovní vrchol označíme indexem 0, tak po konci běhu grafového
automatu budou označeny právě vrcholy s indexy 0, N/3 a 2N/3.
Pokud vám to pomůže, můžete předpokládat, že každý vrchol je spojený hranou
s místním číslem 1 se sousedem po směru hodinových ručiček a hranou
s místním číslem 0 s druhým sousedem (jako na obrázku v úvodu).
Úkol 2 [3b]
Mějme 5-regulární souvislý graf s jedním označeným vrcholem (bude mít na
začátku proměnnou a=1, ostatní vrcholy ji budou mít nulovou). Vaším úkolem
bude najít nějakou kostru tohoto grafu, tedy nějakou podmnožinu hran
takovou, že stále spojuje všechny vrcholy, ale neobsahuje žádný cyklus.
Pro výstup použijte pole proměnných kostra[i] obsahující pět prvků. Na začátku
bude toto pole v každém vrcholu plné nul, na konci by v něm měly být jedničky
právě na pozicích, které odpovídají místním číslům hran, které jsou v nalezené
kostře (pozor, pamatujte na to, že místní a protější číslo hrany nemusejí být
stejné a že je nutné nastavit pole kostra[i] na obou koncích hrany).
V předchozích dvou úkolech stačilo odhadovat počet taktů asymptoticky, nebylo by
ale zajímavé zkusit si vyrobit program, o kterém budeme vědět úplně přesně, jak
dlouho poběží?
Úkol 3 [4b]
Vyrobte program, který bude na K-regulárním grafu na N vrcholech (N≥ 1)
běžet přesně C · N kroků, kde C bude nějaká konstanta, která může záviset na
velikosti K. Pokud se vám však povede C stanovit pevně (bez závislosti
na K), bude to ještě lepší. Pokud vám to pomůže, můžete, jako v předchozích
úkolech, předpokládat, že právě jeden vrchol bude nějakým způsobem označen.
Možná už začínáte být nervózní, už je skoro konec seriálu a ještě nebylo ani
slovo o tradičním uzávorkování. Nebojte se, zde přichází:
Úkol 4 [5b]
Vaším úkolem bude zkontrolovat správnost uzávorkování skládajícího se z levých
a pravých závorek. Správné uzávorkování je takové, kde jsou závorky správně
spárovány a páry se nekříží.
V řeči grafomatu budou závorky zakódované hodnotami ve vrcholech 2-regulárního
grafu (kružnice) na N vrcholech: v prvním vrcholu bude zapsána
první závorka, ve druhém druhá, a tak dále. Poslední vrchol pak bude navíc hranou
spojen s prvním, aby byla kružnice uzavřená.
Závorky budou zapsány pomocí proměnné zavorka a to tak, že hodnota 1 bude
odpovídat levé (otevírací) závorce a hodnota -1 pravé (uzavírací) závorce.
Navíc bude první vrchol označen pomocí prvni=1, aby šel jednoduše poznat.
Na konci běhu by ve všech vrcholech měla být nastavená proměnná vystup na
hodnotu 1, pokud bylo uzávorkování korektní, nebo na hodnotu 0, pokud nebylo.
Pár slov závěrem
S grafomaty jste se již mohli potkat při studování starých ročníků Matematické
olympiády kategorie P. Naše grafomaty jsou velmi podobné (ale ne identické –
třeba se liší v podmínkách zastavování), takže se pro inspiraci můžete podívat i na
studijní texty a úlohy 56. ročníku olympiády.
Možná vám grafomaty přijdou jako zajímavý teoretický model, který nemá s praxí
pranic společného. Opak je však pravdou. Speciální verzí grafomatů jsou třeba
takzvané buněčné automaty a nejznámější z nich je asi Conwayova
hra Život.
Ta se svým fungováním blíží svému biologickému předobrazu – buňky v těle
složitějších organismů jsou také často jedna jako druhá (alespoň v rámci stejné
tkáně) a každá z nich reaguje jen na to, co „vidí“ okolo sebe.
Mimo to grafomat můžeme považovat za jeden z dosti realistických modelů
paralelních počítačů. Z fyzikálních zákonů totiž plyne, že vzdálené procesory
spolu nemohou komunikovat okamžitě (kvůli konečné rychlosti světla) a že každý procesor
může komunikovat pouze s velmi omezeným počtem sousedů (kvůli omezené dimenzi
prostoru). Obě omezení grafomat poměrně věrně zachycuje.
Jirka Setnička
Řešení
 Jacob má před sebou podivné zařízení a chtěl by ho spustit. Jenže předtím musí
vyměnit několik spálených relé. Každé relé má své typové označení (přirozené
číslo), které jde poznat po vyndání relé ze zařízení. Avšak spálená relé mají
označení bohužel spečená k nepoznání.
Jacob má před sebou podivné zařízení a chtěl by ho spustit. Jenže předtím musí
vyměnit několik spálených relé. Každé relé má své typové označení (přirozené
číslo), které jde poznat po vyndání relé ze zařízení. Avšak spálená relé mají
označení bohužel spečená k nepoznání.
 Máme před sebou bednu plnou náhradních kabelů a potřebujeme rychle poznat,
jestli jsou nějaké dva kabely stejné. Nejsou to ale jen kabely se dvěma konci,
tyto jsou rozvětvené a mohou obecně propojovat i více věcí dohromady.
Máme před sebou bednu plnou náhradních kabelů a potřebujeme rychle poznat,
jestli jsou nějaké dva kabely stejné. Nejsou to ale jen kabely se dvěma konci,
tyto jsou rozvětvené a mohou obecně propojovat i více věcí dohromady.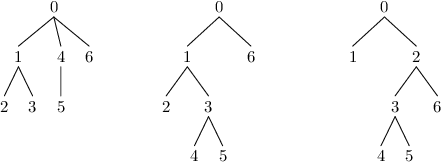

 Vesnický náčelník má k dispozici
Vesnický náčelník má k dispozici 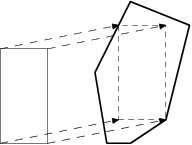

 Ve všech čtyřech minulých dílech tohoto seriálu jsme se potulovali po pomyslné
zoo výpočetních modelů a zastavovali se u zajímavých exemplářů. Dnes naši
letošní pouť zakončíme u jednoho podivného výběhu, ve kterém se nepase
jedno velké výpočetní zvířátko, ale spousta maličkých. Řeč bude o grafových automatech.
Ve všech čtyřech minulých dílech tohoto seriálu jsme se potulovali po pomyslné
zoo výpočetních modelů a zastavovali se u zajímavých exemplářů. Dnes naši
letošní pouť zakončíme u jednoho podivného výběhu, ve kterém se nepase
jedno velké výpočetní zvířátko, ale spousta maličkých. Řeč bude o grafových automatech.