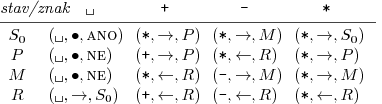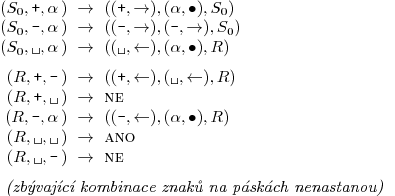První série dvacátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Zadání úloh
Prázdnotu vesmíru prořízl oslepující záblesk. Kde před chvílí byl jenom volný
prostor, nalézaly se teď megatuny hmoty hvězdné lodě. Z trupu se vysunuly
anténní systémy a senzory začaly prozkoumávat okolní prostor.
Mohlo by se to jevit jako standardní skok z hyperprostoru do normálního vesmíru,
nebýt dlouhého roztřepeného šrámu táhnoucího se skoro přes celý levobok. Těsně
nad šrámem se nalézaly ještě stěží rozeznatelné insignie hlásající, že se jedná
o UFC Freya, těžkou nákladní loď Spojené federace.
V tom se objevil další záblesk. Některé z hlavních motorů lodě se spustily
a začaly do prostoru za lodí chrlit gejzíry světla z nukleární fúze tak jasné,
že by se do nich nechráněné lidské oko nemohlo ani podívat. Poškození lodě bylo
příliš rozsáhlé, Freya umírala…
Bylo skoro zázrakem, že se lodi podařilo přežít cestu hyperprostorem v takovémto
stavu. Zdaleka však neměla vyhráno. Hlavní počítač stále zápasil se
selhávajícími systémy a soupeřil o kontrolu nad lodí s poškozenými obvody
vysílajícími do lodních rozvodů nesmyslné příkazy.
26-1-1 Blokující signály (8 bodů)
Hlavní počítač poškozené hvězdné lodě se pokouší obnovit kontrolu nad
většinou důležitých systémů. Bohužel ale poškozené obvody, dříve než je hlavní
počítač zvládl izolovat, vyslaly do lodní počítačové sítě několik vadných
signálů, které je potřeba zastavit, než se dostanou do svého cíle.
Lodní počítačová síť je představována N propojenými počítačovými uzly, mezi
kterými je M přímých spojení (kabel spojující nějaké dva uzly). Síť tedy
vlastně představuje neorientovaný graf.
Každý vyslaný vadný signál je zadaný posloupností uzlů sítě (cestou) a svým cílovým
uzlem. Každou časovou jednotku se posune o jeden uzel na své cestě dál.
Zastavení signálu probíhá tak, že ve vhodný okamžik vyšleme z hlavního počítače
(jeden určený uzel sítě) vhodný blokující signál. Ten cestuje stejnou rychlostí
jako vadný signál, ale může jinou cestou. Když se signály potkají (dorazí
ve stejný čas do stejného uzlu), tak blokující signál zabrání dalšímu šíření
vadného signálu.
Ptáme se, kolik signálů dokážeme zastavit ještě před tím, než dosáhnou svých
cílových vrcholů.
Řešení
Motory postupně ustálily svůj chod a Freya se stabilizovala. Stav však
zůstával kritický, poškozený hlavní reaktor, který byl nyní pod šrámem zčásti
odhalený, stále hrozil výbuchem.
Freya byla transportní loď postavená ještě za války, měla tedy sice
zastaralou, ale snad stále platnou mapu hvězdných soustav. Soustava, do které
s vypětím všech sil dolétla, byla sice daleko od běžných letových tras, ale
obsahovala planetu schopnou udržet lidský život.
Pátrací senzory malou planetu konečně našly, loď mírně změnila svůj kurz
a začala se připravovat na nouzové přistání. Původně měla celý svůj život zůstat
v mezihvězdné prázdnotě a k planetě se přiblížit nejblíže na dosah raketoplánu,
ale poctiví programátoři a konstruktéři ji před lety připravili i na tuto
eventualitu. Devatenáct lidí v kryogenickém spánku stále nic netušilo…
26-1-2 Přeskládání nákladu (9 bodů)
Hvězdná loď potřebuje připravit svůj náklad na nouzové přistání. Přípravy
spočívají mimo jiné v tom, že se musí rozdělit, který náklad bude ve skladišti
na pravoboku a který na levoboku.
Náklad je tvořen celkem N kontejnery. Z důvodu bezpečnosti a rovnoměrného
rozložení zásob (aby jich bylo dost i v případě ztráty jednoho skladiště)
existuje také M doporučení. Každé doporučení říká, že nějaká dvojice
kontejnerů by neměla být v tom stejném skladišti.
Všechny předpisy najednou pravděpodobně splnit nepůjde, ale hlavní počítač chce
nalézt rozdělení kontejnerů do skladišť (množství kontejnerů v jednotlivých
skladištích nemusí být stejné) takové, aby byla splněna alespoň polovina
doporučení.
Řešení
Dopravníky uvnitř lodi dokončily přesuny kontejnerů, loď přečerpala zásoby
paliva tak, aby kompenzovala vyvážení, a byly uzavřeny všechny vzduchotěsné
dveře.
Hlavní motory už nějakou chvíli nepracovaly, jejich další chvíle měla přijít
v konečné fázi sestupu. Freya pomalu klesala do atmosféry planety. Jak se
začala třít o horní vrstvy atmosféry, tak její příď postupně změnila barvu přes
temně rudou až do jasné oranžové. Okolo trupu začaly šlehat plameny a trupové
nástavby začaly odletovat jedna za druhou. Během chvíle zmizely pátrací radary,
jeřábové manipulátory i zbytky poškozených komunikačních antén.
V přesně vypočtenou chvíli naběhly přední manévrovací motory. Nebyly stavěné
jako brzdící, ale jejich předimenzovaná velikost a spuštění na kritický výkon by
mohly stačit, pokud ten nápor vydrží.
Loď zpomalovala. V tom ale její pravobok pohltil oslňující výbuch. Zdejší vrchní
vrstva atmosféry obsahovala nějaké kapsy výbušných plynů. Tentokrát to odneslo
jen skladiště na pravoboku, ale další takový výbuch by mohl loď rozpůlit.
Hlavní počítač vysunul jeden z posledních fungujích radarů. Ve zlomku sekundy,
než ho proud vzduchu vyrval z trupu, stihl zaznamenat rozložení kapes plynů
v atmosféře.
26-1-3 Plynové kapsy (8 bodů)
Snímkovací radar dodal průřez atmosférou obsahující dva druhy plynů. Průřez je
znázorněn v podobě posloupnosti znaků a a b (dva druhy plynů) délky N.
Pro loď širokou dva znaky je bezpečné proletět skrz souvislou oblast buď
jednoho, nebo druhého plynu. Na rozhraní plynových kapes je to moc nebezpečné
(tedy může proletět oblastí aa, bb, ale nemůže proletět místem, kde se
setkávají – ab nebo ba).
Hlavní počítač potřebuje vytvořit datovou strukturu, které by se mohl rychle
ptát, kolik míst k průletu je v zadaném intervalu. Tedy kolik v něm je stejných
sousedních polí.
Počítejte s tím, že dotazů bude řádově N a že počítáme i ta místa, která se
vzájemně překrývají.
Příklad: Výstup z radaru a odpovědi na dotazy na intervaly (indexujeme od
nuly):
Radar: aababbaaa
[0,7] -> 3 místa
[0,8] -> 4 místa
[2,4] -> 0 míst
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Po dalším výbuchu vzplál jeden z brzdících motorů, a proto ho nouzový systém
i s okolní sekcí odhodil. Explodoval v obrovskou kouli ohně těsně za lodí. To se
však už Freya dostala do spodních vrstev atmosféry.
Kdyby se hlavní počítač mohl divit, asi by se teď divil. Ale nic takového neměl
ve svém programu, a tak jen provedl rychlý výpočet, aby se nějak vypořádal
s údaji o mnohem vyšší rychlosti, než byla původně plánovaná.
Hlavní motory podruhé naběhly, tentokrát s tryskami obrácenými na reverzní tah.
Počítač vyřadil všechny pojistky a spustil je na výkon, na který ještě nikdy
neběžely. Za lodí zůstával pruh doslova spálené atmosféry.
Loď brzdila s takovým přetížením, že začaly povolovat vnitřní přepážky. Jedno
z kryogenních oddělení, společně s celým levobočním hangárem, vylétlo z lodi
a zaniklo v záři atomového ohně motorů. Odletovaly kusy trupu a konstrukce se
bortila.
Byla to dobře postavená loď, ještě podle válečných specifikací. Dnešní lodě by
se už dávno rozpadly, Freya však držela dál. Pak ale přišla i její chvíle.
Nejdříve se v půlce trupu zkroutila a zanedlouho se celá zadní
polovina třísetmetrové lodě utrhla společně se všemi hlavními motory.
Svou práci však hlavní motory vykonaly, zbrzdily sestup. Zatím stále funkční
přední část pokračovala v řízeném pádu korigovaném manévrovacími motory. Pak
dopadla. Odrazila se a dopadla podruhé. Vyryla v místním ekvivalentu deštného
pralesa brázdu dlouhou skoro tři kilometry a pak se konečně zastavila…
* * *
Jacob otevřel oči. Nad ním se nacházel otevřený poklop jeho kryogenní kóje.
Otřepal z rukou poslední zbytky kryogenního gelu a protřel si oči.
„Tak počkat, tady něco nehraje!“ pronesl pomalu při pohledu na rozbitou
místnost, do níž odněkud prosvítalo podivné žluté světlo. Vyhoupl se z kóje
a přistál bosýma nohama na nakloněné podlaze.
Druhá strana místnosti, na které se nacházely zbylé kóje, byla celá zavalená.
Pomocí kusu nosníku se mu povedlo roztáhnout dveře a skrz trosky se prodral na
chodbu a k nejbližšímu počítačovému uzlu, aby zjistil, co se stalo.
26-1-4 Oprava databáze (10 bodů)
Databáze hlavního počítače je silně poškozena a samoopravný mechanismus je
vyřazen. Musíme ji proto opravit ručně. Jak ale poznat, že jsme ji sestavili
správně? Jistá naděje tu je: víme, že databáze měla podobu posloupnosti celých
čísel, a počítač si pamatuje, kolik v ní bylo trojných prvků.
Trojný říkáme takovému prvku, který se dá poskládat jako součet nějakých tří
předchozích prvků v posloupnosti. (Dodejme ještě, že jeden prvek nemůžeme
v součtu použít vícekrát, ale dva prvky téže hodnoty už ano.)
Příklad: Pro posloupnost 1,4,7,2,7,16,10 jsou trojnými prvky druhá
sedmička (7=1+4+2), šestnáctka (16=7+2+7) a desítka (10=1+2+7), jiné
trojné nejsou. První sedmička není na rozdíl od druhé trojná, protože
u ní ještě nemůžeme použít číslo 2.
Lehčí varianta (za 6 bodů): Vyřešte úlohu pro případ, kdy hledáme dvojné prvky namísto
trojných (tedy skládáme jen ze dvou předchozích prvků v posloupnosti).
Řešení
Když Jacob zjistil, co se stalo, chvíli stál naprosto bez pohnutí. Potom udeřil
pěstí do přepážky.
„Zatraceně, tak jsem jediný přeživší na téhle planetě, která dokonce ani nemá
jméno!“
Když se trochu vzpamatoval, začal postupovat směrem k bývalému můstku. Cestou se
zastavil ve výstrojním skladu a z hromad popadaných beden vylovil nějaké
základní věci jako baterku, nůž, lékárničku a nějaký batoh. Taky se převlékl do
odolnější kombinézy a vzal si boty.
Po dalších několika minutách zjistil, že můstek lodě již neexistuje. Místo toho
se mu však naskytl pohled na okolní prales. Stromy nevypadaly zase tolik jinak
než ty pozemské. Měly trochu jinou barvu a byly hlavně mnohem vyšší. Převyšovaly
o pár metrů dokonce i zabořené torzo lodě.
Věnoval ještě asi hodinu průzkumu, během něhož obešel většinu lodě. Nakonec
vylezl po již dávno vychladlém trupu na nejvyšší místo a posadil se pozoruje
dlouhou brázdu od pádu lodě.
„Prales…To znamená, že tu asi bude nějaký mimozemský život. A nemusel by
být úplně přátelský,“ zamyslel se Jacob nahlas. Už se také stmívalo a z lesa se
začínaly ozývat podivné zvuky. Chtělo by to asi okolí nějak zajistit. Shodou
okolností Freya zrovna převážela senzorové soupravy, které by mohl použít.
Vypravil se tedy do trosek skladu a rychle vytáhl několik funkčních senzorových
věží a pár desítek metrů kabelů.
26-1-5 Senzory (10 bodů)
Chceme rozestavit K senzorových věží na čtvercovou síť o rozměrech
M×N. Pro správnou funkci senzorů je potřeba, aby žádné dvě senzorové
věže nestály ve stejném sloupci nebo na stejném řádku.
Každá senzorová věž má navíc určený obdélník, ve kterém musí být postavena.
Najděte pro dané zadání nějaké fungující rozestavení věží nebo určete, že takové
rozestavení neexistuje.
Lehčí varianta (za 6 bodů): Vyřešte úlohu pro případ, že sít má tvar jednořádkové „nudle“
(tedy M=1) a dvě věže nesmí stát v témže sloupci.
Řešení
Po zapojení poslední věže do systému se Jacob uložil ke spánku v bývalé jídelně.
Druhý den na planetě již probíhal trošku poklidněji. Po dalším průzkumu lodě
zjistil, že má celkem dostatečné zásoby pitné vody a že nouzové palivové články
mu budou schopny dodávat energii ještě přinejmenším rok, pokud se mu do té doby
nepovede znovu nahodit záložní reaktor.
Mnohem větší problém byl ale s jídlem. Hlavní sklad jídla se totiž nacházel
v zadní části lodě a vepředu byla jen hydroponická zahrada, která navíc při
přistání dost utrpěla. Jelikož nechtěl zatím zkoušet ochutnávat místní jídlo,
rozhodl se Jacob hydroponiku opravit.
26-1-6 Hydroponie (11 bodů)
Hydroponická zahrada je tvořena soustavou N očíslovaných přihrádek na
rostliny, v každé může být maximálně jedna rostlina (ale také tam nemusí být žádná).
Mimo to je zde M napájecích okruhů, každý napojený na určitý interval
přihrádek.
V každém napájecím okruhu chceme mít umístěnou dohromady minimálně jednu
rostlinu, jinak nám na rozmístění a počtu rostlin nezáleží.
Ptáme se na počet možných způsobů, jak můžeme obsadit přihrádky rostlinami tak,
aby byly splněny výše zmíněné podmínky. Jelikož počet může být obrovský,
spočítejte ho modulo 1 000 000 007.
Řešení
Jacob zrovna přemístil poslední rostlinku, když v tom se ozval z chodby poplach.
To počítač napojený na senzory nahlásil, že něco velkého porušilo perimetr.
Jacob popadl velký nůž a vyběhl ven.
Doběhl na místo, odkud senzory hlásily narušitele. Na zemi tam byly v bahně
obtisknuté nějaké stopy a… V Jacobovi hrklo, vedle stop ležel umně vyrobený
a nazdobený malý oštěp. To znamená, že je tady inteligentní život! To musí
prozkoumat!
Natěšený doběhl nazpět do torza lodi, během pěti minut si pobral zásoby jídla
a vody na několik dní, sbalil si lékárničku, kameru a další potřebné věci
a vydal se opět na místo, kde nalezl ten oštěp.
Vydal se opatrně po stopách směrem do lesa. Po několika metrech přišel na malý
palouk, kde ho zaujal místní podivný hmyz. Podobal se trochu pozemským
mravencům, jen byl mnohem větší. Zvedl kus klacku s několika těmito tvory
a chvíli je pozoroval.
26-1-7 Mravenci (8 bodů)
Tvorové podobní mravencům lezou po rovném kusu klacku dlouhém D centimetrů. Na
začátku se jich zde nachází N a každý tvor se pohybuje buď doprava, nebo
doleva, a to rychlostí jednoho centimetru za sekundu.
Když tvor přijde na konec klacku, tak spadne. Když se dva tvorové potkají, tak
se oba otočí čelem vzad. Nás zajímají dvě věci:
a) (za 3 body) Za kolik sekund z klacku spadne poslední tvor?
b) (za 5 bodů) Na jaké pozici tento tvor na začátku stál?
Tvory v této úloze považujte za zanedbatelně malé vzhledem k velikosti klacku.
Řešení
Od pozorování tvorů na klacku náhle Jacoba vyrušilo zapraskání za jeho zády.
Rychle se otočil a…
Pokračování příště…
Úvodem dobrodružství na neznámé planetě vás provedl
Jirka Setnička
26-1-8 Turingova strojovna (12 bodů)
Při řešení KSP po vás obvykle chceme, abyste na daný problém sestrojili
algoritmus. Přemýšleli jste někdy nad tím, co to takový algoritmus přesně je?
Intuitivně je to jasné: nějaký zápis postupu, jak něco spočítat, poskládaný
z dostatečně jednoduchých kroků. To se ale sotva dá pokládat za pořádnou
definici.
Tak jinak: algoritmus je totéž co program v našem oblíbeném
programovacím jazyce, jen zbavený přízemních detailů (třeba omezené velikosti
datových typů). Je to lepší? O moc ne – sice už je jasné, co to znamená,
ale zase se nám definice rozrostla o specifikaci celého programovacího jazyka
(umíte popsat Céčko nebo Python jedním odstavcem? stránkou? knížkou?). A navíc
ani není jasné, jestli pro nás algoritmus znamená totéž jako pro dědečka
Pascalistu nebo pro pradědečka, který ještě programy děroval ve strojovém kódu.
Dobrá, jaká je tedy správná definice? Teoretičtí informatikové obvykle postupují tak,
že si zavedou nějaký výpočetní model. Tím se myslí jednoduchý matematický stroj
s přesně určenými operacemi, řízený programem. Za algoritmus pak prohlásíme
program pro tento stroj. Na první pohled to vypadá, že jsme se z deště přesunuli
pod okap, ale přeci jen tu prší méně: Výpočetní modely jsou daleko jednodušší
zviřátka než běžné programovací jazyky (však za chvíli uvidíme). Navíc není těžké
o různých výpočetních modelech dokázat, že dovedou spočítat totéž, takže nezáleží
na tom, který z nich jsme pro zavedení algoritmu použili.
V letošním seriálu se spolu vydáme na procházku po zoo výpočetních modelů.
Výběhů tu je habaděj, my se zastavíme u pěti z nich a pokaždé si v daném modelu
zkusíme něco naprogramovat a třeba i dokázat pár obecných větiček o jeho
vlastnostech. Mezitím můžete sami rozmýšlet, jak do každého modelu překládat
programy z vašeho oblíbeného jazyka. Pěknou cestu!
Turingovy stroje
Nejklasičtějším a nejspíš i nejstarším modelem počítače je bezpochyby
Turingův stroj. Alan Turing ho popsal v roce 1936 ve své práci, kterou
položil základy matematického zkoumání počítačů.
TS je vybaven oboustranně nekonečnou páskou rozdělenou na políčka. Na každém
políčku je zapsán jeden znak ze zvolené abecedy. Tou se myslí nějaká
množina znaků, o níž víme jen to, že je konečná a že obsahuje mezeru
(tu značíme ␣).
Nad páskou se pohybuje hlava. Vždy se nachází nad jedním políčkem a umí
z něj přečíst znak a případně ho přepsat na jiný.
Činnost stroje ovládá řídicí jednotka podle programu. Řídicí
jednotka se v každém okamžiku nachází v jednom z konečně mnoha stavů. V každém
kroku výpočtu se podívá, v jakém stavu S se nachází a jaký znak z vidí hlava,
a podle toho vybere jednu instrukci programu. Ta stroji říká, že má znak z
přepsat na z', posunout hlavu o políčko v daném směru a nakonec se přepnout do stavu S'.
Program tedy můžeme popsat tabulkou, jejíž řádky odpovídají možným stavům S,
sloupce znakům z a v každé buňce tabulky je uložena jedna instrukce v podobě
trojice (z',p,S'). Instrukce říká, co má stroj ve stavu S, který přečetl znak z, udělat.
Tedy zapsat znak z', posunout se ve směru p ∈{ ←, →, •}
(o políčko doleva či doprava, případně zůstat na místě) a přejít do stavu S'.
Nyní definujeme výpočet stroje. Na počátku výpočtu je na pásce zapsán
vstup, hlava stroje stojí na začátku vstupu a zbytek pásky je vyplněn
mezerami. Řídicí jednotka se nachází ve zvoleném počátečním stavu S0.
Výpočet probíhá v krocích (taktech) – v jednom kroku stroj provede
jednu instrukci programu (přečte znak, rozhodne se podle tabulky, zapíše znak,
posune hlavu, změní stav). Tak pokračuje až do doby, kdy se dostane do některého
z koncových stavů.
Koncové stavy budeme mít dva a budeme jim říkat ano a ne, čímž umožníme
stroji, aby výpočet ukončil úspěšně nebo neúspěšně. Pokud chceme, aby výsledkem
výpočtu bylo něco víc než jediný bit, dohodneme se, že výstup bude opět napsán
na pásce, obklopen mezerami.
Dodejme ještě, že vždy hledáme jeden TS, který danou úlohu vyřeší pro všechny
vstupy – počet stavů, velikost abecedy nebo obsah programu nesmí záviset
na vstupu. Pak můžeme snadno definovat časovou a prostorovou složitost.
Čas budeme měřit počtem provedených instrukcí, prostor počtem políček pásky,
jež během výpočtu navštívila hlava stroje. Nezapomeňme, že mohou existovat
i výpočty, které se nikdy nezastaví; ty pak mají nekonečnou časovou složitost
a možná i nekonečnou prostorovou.
Příklad
Suchá formální definice bude stravitelnější, když ji doplníme příkladem.
Sestrojíme TS, který dostane řetězec složený ze znaků + a -,
vždy se zastaví a odpoví ano právě tehdy, když je vyvážený. Tím
myslíme, že obsahuje stejně plusek jako minusek.
Stroj bude na pásce opakovaně hledat dvojice znaků + a - (ne nutně
vedle sebe) a oba znaky přepisovat na *. Vyvážený vstup tedy nutně předělá
na samé hvězdičky. Jestliže vstup vyvážený není, zbude nakonec jedno +,
ke kterému už neexistuje -, či opačně.
Za abecedu stroje zvolíme množinu { ␣, +, -, * },
řídicí jednotka bude vybavena stavy { S0, P, M, R, ano, ne } a
následujícím programem:
Ve stavu S0 hledáme první znak různý od *. Pokud je to +, přejdeme do stavu P,
v němž hledáme - do páru. Podobně stav M odpovídá tomu, že jsme našli - a hledáme
párové +. Po nalezení páru pokračujeme stavem R, který hlavu stroje vrátí zpět na začátek
vstupu a pak přejde na hledání dalšího páru, tedy do stavu S0.
Časová složitost tohoto stroje pro vstup délky n činí O(n2), neboť na vstupu
se vyskytuje až n párů znamének a každý z nich můžeme hledat až O(n) kroků.
Paměti spotřebuje O(n) políček.
Úkol 1 [3b]
Navrhněte Turingův stroj, který dostane posloupnost závorek ( a )
a odpoví ano nebo ne podle toho, zda je vstup správně uzávorkovaný.
Tím myslíme, že závorky jsou správně spárované a páry se nekříží. Například
na vstupy ()() a (()()) odpoví ano a na )()( odpoví ne.
Součástí řešení úkolu by měl být kompletní popis stroje: abeceda,
množina stavů, program. Sluší se též spočítat, jakou má stroj časovou
a paměťovou složitost.
Vícepáskové stroje
Možná vás překvapilo, že stroj z předchozího příkladu potřeboval na tak obyčejnou
věc, jako rozpoznání vyváženosti, kvadratický čas. Zčásti to bylo způsobené
naší nešikovností (zkuste sestrojit jiný stroj, který tutéž úlohu zvládne rychleji),
zčásti tím, že musíme neustále přejíždět hlavou mezi různými místy, která nás
zajímají současně.
Často se proto uvažuje vícepásková varianta Turingova stroje. Ta má libovolný počet
pásek (budeme ho značit p) a na každé pásce samostatnou hlavu.
Řídicí jednotka se pak rozhoduje podle kombinace symbolů viděných jednotlivými hlavami.
Program proto není 2-rozměrná tabulka, nýbrž (p+1)-rozměrná (jeden rozměr odpovídá
aktuálnímu stavu stroje, ostatní přečteným znakům). Instrukce programu pak říkají
každé hlavě, jaký symbol má na svou pásku zapsat a kterým směrem se má posunout;
různé hlavy se mohou pohybovat různě, nebo zůstat stát.
U vícepáskových TS bývá zvykem, že jedna z pásek je vyhrazena pro vstup
a jiná pro výstup. Na vstupní pásce je na počátku vstup, stejně jako u jednopáskového TS.
Ostatní pásky ze začátku obsahují samé mezery. V průběhu výpočtu smí program ze
vstupní pásky pouze číst a na výstupní pouze zapisovat; ostatní pásky (těm se říká
pracovní) může využívat libovolně. Do prostorové složitosti se pak počítají
pouze políčka na pracovních páskách.
Příklad podruhé
Předveďme si, jak úlohu s plusky a minusky vyřešit rychleji za pomoci stroje
se dvěma páskami: jednou vstupní a jednou pracovní (jelikož odpovídáme pouze ano/ne,
výstupní pásku nepotřebujeme).
Půjde to snadno: nejprve projdeme vstup a všechna - zkopírujeme na pracovní
pásku. Poté vstup projdeme podruhé a za každé + smažeme jedno - z pracovní
pásky; pokud už tam žádné není, odpovíme ne. Na konci ověříme, zda je pracovní páska
prázdná, a podle toho odpovíme ano nebo ne.
Stroj pracuje s abecedou { +, -, ␣ }
a stavy { S0, R, ano, ne }. Jeho program vypadá následovně:
Jelikož trojrozměrnou tabulku neumíme nakreslit, popsali jsme ji pomocí pravidel
(S,x,y) →((x',p),(y',q),S'). Tím myslíme: jsme-li ve stavu
S
a vidíme-li na vstupní pásce znak
x a na pracovní znak
y, pak na vstupní
pásku zapíšeme
x' a provedeme posun
p, na pracovní pásku zapíšeme
y' a provedeme
posun
q; nakonec přejdeme do stavu
S'. Symbol
α značí libovolný
znak abecedy, na levé straně pravidla stejný jako na pravé. Jelikož na vstupní pásku není
povoleno zapisovat, tváříme se, jako bychom tam vždy zapisovali to, co tam
už je. Pokud zastavujeme výpočet, píšeme prostě
ano či
ne a nestaráme
se, co stroj udělá s páskami.
Náš nový stroj pracuje v lineárním čase (vstup projde všeho všudy
dvakrát) a spotřebuje lineární množství prostoru.
Úkol 2 [5b]
Vyřešte první úkol na vícepáskovém Turingově stroji. Snažte se dosáhnout
co nejlepší časové i paměťové složitosti.
Úkol 3 [2b]
Dokažte, že každý Turingův stroj jde upravit, aby si vystačil pouze
se dvěma stavy (kromě ano a ne). Počítat musí samozřejmě stále
totéž, byť třeba pomaleji.
Úkol 4 [2b]
Ukažte, jak vyřešit předchozí úkol pro jednopáskové stroje tak,
aby zůstaly jednopáskovými.
Poznámky
S Turingovými stroji se řešitelé KSP potkali už jednou: zabýval
se jimi seriál 14. ročníku. Zkuste se
na jeho zadání i řešení podívat, skrývá se tam nejedna další
zajímavost. Letošní úlohy jsou ale samozřejmě řešitelné i bez toho.
Zkoušeli jsme zesílit TS přidáním dalších pásek. Co kdybychom ho
naopak chtěli trochu oslabit? Nabízí se nahradit přepisovatelnou
pásku „děrnou páskou“ – v abecedě existuje speciální znak
„díra“ a stroj má povoleno pouze přepsat mezeru na libovolný
znak a nemezerový znak na díru. V úloze 14-4-5 se dokazuje, že
takový TS je stejně silný jako ten klasický.
V omezování TS bychom mohli ještě pokračovat: mohli bychom úplně
zakázat zápis, takže stroj by směl jenom pohybovat se po pásce a číst
(jinými slovy měl by jenom vstupní pásku a žádné pracovní).
Takový stroj už je mnohem slabší, konkrétně ekvivalentní s konečnými
automaty, které jste mohli potkat v seriálu 23. ročníku.
Martin Mareš
Řešení
