Pátá série dvacátého ročníku KSP
Celý leták v PDF.
Milí řešitelé!
Jubilejní 20. ročník KSP je úspěšně za námi a ti nejlepší z vás se mohou těšit na závěrečné soustředění. Než se ale pustíme do rozebírání úloh poslední série, připravili jsme si pro vás malé překvapení. Poprosili jsme našeho Hrošíka, aby nám věnoval pár minut ze svého nabitého programu (to víte, šéfuje celému KSP a přitom musí alespoň 22 hodin denně spát) a poskytl nám exkluzivní interview.
 Dobrý den.
Dobrý den.
Huiii.
Rádi bychom vám položili několik otázek týkajících se vedení KSP, máte chvilku…
Ale opravdu jen chvilku – za pět minut mi začíná druhý oběd.
Naše řešitele a řešitelky by zajímalo, co je na vedení KSP nejtěžší.
Někdo by myslel, že nejtěžší je vymýšlení nebo opravování úloh. Bohužel to není pravda. Nejtěžší je ukočírovat tu nezodpovědnou bandu organizátorů. Sehnat dneska dobrý materiál je opravdu těžké, a tak se musíme spokojit s tím, co máme.
To je zajímavé. A pomáhá vám…váš živočišný druh – tedy myslím jako to, že jste hroch – ve vaší těžké funkci?
Myslím, že trochu ano. Víte, tlustokožci budí přirozený respekt, takže si nikdo nedovolí odporovat mi. Také mám velkou tlamu, takže můžu kohokoli bez potíží seřvat – ehumpf, to tam nepište. Napište tam, že si můžu s každým cokoli vyříkat, to bude znít lépe.
To musí být praktické, ale nepovažoval jste to – ehm, bytí hrochem – také někdy za nevýhodu?
Občas. Víte, už nejsem tak mrštný, jako kdysi. Taky musím hodně jíst a spát, znáte to…
Obraťme list, co považujete za největší pozitivum KSP?
Myslím, že nejlepší na KSP je, co všechno dělá pro mládež. Je mnohem lepší, aby středoškoláci seděli doma u počítače a programovali, než aby se flákali někde po různých sportech nebo dokonce běhali za holkama.
Nyní se dotknu citlivějšího tématu. Myslíte si, že je KSP lepší než ostatní semináře?
Víte, takovéhle srovnávání seminářů není úplně korektní, protože ostatní semináře se zabývají jinými obory, takže neexistuje objektivní metrika (promiňte mi ten matfyzácký výraz), pomocí které bychom je mohli porovnávat. Nicméně pokud otázku přeformulujeme jinak – například zda je informatika lepší než řekněme fyzika – tak je odpověď jasná: Informatika je lepší než všechny ostatní vědy.
To je dost silný názor…nemyslíte si, že by s ním třeba fyzikové nesouhlasili?
To je možné. Můžou s ním nesouhlasit, můžou proti němu i protestovat, ale to je asi tak všechno, co se s tím dá dělat.
A víte, že v řadách organizátorů je i jeden fyzik?
Vím. A také dva matematici, ale co se dá dělat. Jak jsem již řekl na začátku, musíme brát to, co je.
Raději přejdeme na jiné téma. Co děláte pro zábavu? Sledujete třeba Euro?
No, občas se podívám…naposledy byl kurz ke koruně okolo 25,-, ale nevím, co na tom vidíte zábavného.
Á-ha – tak snad už jen poslední otázku…jaké jsou plány KSP na příští rok?
Příští rok chceme pokračovat v rozjeté tradici a neplánujeme žádné velké změny. Detaily ohledně připravovaného seriálu a příběhu k úložkám raději vynechám, abych nezkazil překvapení. Áá – už mi vezou oběd…
Naše interview je u konce. Přeji vám za všechny organizátory pěkné prázdniny a hodně úspěchů v dalších ročnících.
Ještě bychom Vás chtěli, jako už několikrát, poprosit: myslíme si, že je škoda, že se našeho semináře účastní tak málo řešitelů. Budeme rádi, když nám na začátku příštího roku pomůžete s „reklamou“ – například pověšením zadání první série na školní nástěnku, …
Řešení úloh
- 20-5-1: Dračí cestování
- 20-5-2: Piškorcův deratizátor
- 20-5-3: Obrana před draky
- 20-5-4: Dračí chodbičky
- 20-5-5: Roztržitý matematik
- 20-5-6: Hrady, hrádky, hradla
20-5-1 Dračí cestování (Zadání)
Protože drak je velmi inteligentní zvíře, před cestou si dobře rozmyslel, že každá cesta z překladiště do překladiště ho stojí drahocennou síru, takže je určitě dobré počet cest minimalizovat a nosit vždy co nejvíc jde. Náklad 14000 kg se dá rozdělit na 3 náklady po 4200 kg a jeden 1400 kg těžký. Tím pádem musí absolvovat celkem 7 cest (4 cesty tam a 3 zpátky) na přenesení celého nákladu na první překladiště. Kdyby mu ale v nějakém momentu zbylo jenom 12600 (3·4200) kg síry, dokázal by ji odnést na 5 cest. Pro 8400 kg by se musel vracet jenom jednou, což dělá jenom 3 cesty a 4200 kg unese najednou. Drak si okamžitě uvědomil, že překladiště se mu nejvíc vyplatí dělat tak, aby mu v něm zbylo o jednu várku síry míň než právě má, aby to dokázal odnést na méněkrát. Proč je každé jiné rozložení překladišť horší nebo nanejvýš stejně dobré? Zaveďme si značení: Nechť S(A) je množství síry v překladišti A, N nosnost draka, SP jeho spotřeba na kilometr, V(A,B) vzdálenost mezi překladišti A a B a M(A, B) množství síry, které je drak schopný přenést z překladiště A do překladiště B. Je celkem snadné vidět, že počet cest, které musí drak uletět na přenesení nákladu z překladiště A do překladiště B je roven horní celé části z S(A)/N vynásobené dvěma (drak se musí vracet) mínus jedna (poslední várku se už nevrací). Tím pádem M(A,B) = S(A) - počet cest·V(A,B)·SP (tolik toho drak sní po cestě). Z toho ale vyplývá, že kdyby sme nějaké překladiště posunuli dál, pak by drak letěl zbytečně kousek trasy o dvě cesty víc (tam a zpátky), i kdyby už nemusel, čím spotřebuje víc síry. Naopak, kdybychom posunuli nějaké překladiště o kousek blíž, zbylo by na tom překladišti víc síry a drak by musel k dalšímu stanovisti letět zase o dvě cesty víc (protože by ji neunesl na míň cest, kousek by mu tam zbyl). Taky je jednoduché vidět, že dělat si ještě nějaké překladiště navíc nemá smysl, protože jestli projde část trasy na n-krát a pak druhou část trasy taky na n-krát, spotřebuje přitom stejné množství síry jako kdyby letěl celou trasu na n-krát (počet cest·V1·SP + počet cest·V2·SP = počet cest·(V1+V2)·SP) a tím taky stejné množství síry přenese. Když jsme si tedy dokázali optimální rozložení překladišť, snadno podle toho spočítáme maximální množství síry, které je drak schopný přenést na 4200 kilometrovou vzdálenost. Drak si dělá stanoviště tak, aby na dalším stanovišti zbylo o jednu várku míň než má, tj. v takové vzdálenosti, aby při přenosu spotřeboval právě jednu várku. První překladiště si tedy drak zřídí 1400/7 = 200 km od startu. Tím se zbaví jedné várky. Další várky se zbaví za 4200/5 = 840 km, další za 4200/3 = 1400 km. Nyní je drak 1760 km od cíle a na překladišti má už jenom jednu 4200 kilogramovou várku. Tu si naloží na záda a domů se vrátí s 2440 kg síry.
20-5-2 Piškorcův deratizátor (Zadání)
A nejhorší ze všeho jsou trpaslíci, ty potvory vám vlezou všude a strašně rychle se množí. Já je chytám a většinou je zahazuju, ale mám švagra a ten si je nechává na chov…
Protože Temný mág není zdaleka jediný, kdo má se skřítky problémy, pojďme si říct, jak na ně.
Je jednoduché si uvědomit, že čarodějnice může každý den kouzlit vždy jako první. Pokud by v optimálním plánu kouzlila čarodějnice až po kouzelníkovi, mohla klidně kouzlit i před ním. Dále zajisté platí, že pokud může poté kouzelník provést deratizaci, musí ji provést ihned. Pokud by totiž čekal alespoň den, ztrojnásobil by se počet skřítků a on by místo jedné deratizace musel provádět tři.
Jeden den deratizace probíhá tak, že čarodějnice se rozhodne, jak změní populaci skřítků. Poté kouzelník sesílá deratizační kouzlo, dokud není skřítků méně než N. Tedy pouze čarodějnice má možnost volby. A pokud deratizace neskončila (nějací skřítci zůstali), jejich počet skřítků se ztrojnásobí a deratizace pokračuje.
Problém převedeme na hledání nejkratší cesty v grafu. Uvažujme graf s vrcholy očíslovanými 0 až N-1. Hodnota vrcholu odpovídá počtu skřítků na konci dne (po kouzlení, ale před trojnásobením). Hrana z vrcholu i do vrcholu j znamená, že se po jednom dni deratizace změní počet skřítků z i na j. Z každého vrcholu vedou nejvýš tři hrany, protože čarodějnice si může vybrat ze tří možností. Hrany v tomto grafu budou ohodnocené a ohodnocení hrany bude počet mágem seslaných deratizačních kouzel, tedy číslo 0, 1 nebo 2.
Nejkratší cesta v tomto grafu z vrcholu K-1, K či K+1 do vrcholu 0 je určitě řešením naší úlohu. Jak nejrychleji takovou hranu nalézt? Pokud by hrany nebyly ohodnocené, stačilo by použít prohledávání do šířky (pokud nevíte, co to je, nastal dobrý čas pro přečtení kuchařky třetí série 20. ročníku KSP). Protože jsou ale hrany ohodnocené jenom hodnotami 0, 1 a 2, můžeme upravit prohledávání do šířky následovně: nebudeme mít jednu, ale tři fronty F0, F1 a F2. Ve frontě Fi budeme mít vrcholy, do kterých se dostaneme po provedení i deratizačních kouzel. Vrcholy budeme vybírat jenom z F0 a jejich nenavštívené sousedy, do kterých vede hrana s ohodnocením j, budeme ukládat do fronty Fj. Když nám fronta F0 dojde, uděláme z F1 novou frontu F0, z F2 novou frontu F1 a nová F2 bude prázdná. Tak zaručíme, že vrcholy budeme zpracovávat v pořadí rostoucího počtu deratizací, které potřebujeme, abychom se do těchto vrcholů dostali.
Časová složitost tohoto postupu je O(N), protože graf se skládá z N vrcholů a 3N hran, při upraveném procházení navštívíme každý vrchol nejvýš jednou a každého souseda umíme zpracovat v konstantním čase. Paměťová složitost je zřejmě také lineární.
 …to přece musí jít lépe! A taky že jo.
Je možné dokázat, že stačí najít postup, který zabere
co nejméně dní, protože takový postup použije nejmenší
možný počet deratizačních kouzel. (Není to zas tak těžké,
zkuste si to!) Poté je už řešení v čase O(log N)
nasnadě: na konci nultého dne jsou možné počty skřítků
K-1, K a K+1. Na konci prvního 3K-4, … , 3K+4,
konci i-tého 3iK-(3i+1-1)/2 až 3iK+(3i+1-1)/2,
přičemž jde dosáhnout každého počtu mezi. Stačí tedy najít
první interval takového tvaru, který obsahuje násobek N-ka.
…to přece musí jít lépe! A taky že jo.
Je možné dokázat, že stačí najít postup, který zabere
co nejméně dní, protože takový postup použije nejmenší
možný počet deratizačních kouzel. (Není to zas tak těžké,
zkuste si to!) Poté je už řešení v čase O(log N)
nasnadě: na konci nultého dne jsou možné počty skřítků
K-1, K a K+1. Na konci prvního 3K-4, … , 3K+4,
konci i-tého 3iK-(3i+1-1)/2 až 3iK+(3i+1-1)/2,
přičemž jde dosáhnout každého počtu mezi. Stačí tedy najít
první interval takového tvaru, který obsahuje násobek N-ka.
20-5-3 Obrana před draky (Zadání)
Udatných drakobijců bylo mezi našimi řešiteli pomálu, takže většinu stačil drak skolit dříve, než stačili mrknout. Tak alespoň posmrtně si můžeme předvést, jak hledat místo pro vypuštění mocného protidračího kouzla.
Nejdřív si uvědomíme, že pokud máme kružnici, která obsahuje optimální počet temných kamenů, můžeme ji vždy posunout tak, aby na její hranici byly alespoň dva zadané body (alias temné kameny).
Jednoduchý algoritmus je nyní nasnadě: pro každé dva body najdeme kružnice, na kterých tyto dva body leží. Protože poloměr kružnice je pevně dané R, existují takové kružnice nejvýš dvě. Celkem tedy máme O(N2) kružnic a víme, že jedna z nich je optimální. Stačí tedy pro každou z těchto kružnic zjistit, kolik je v ní zadaných bodů, což můžeme udělat jednoduše v lineárním čase. Tak získáme řešení s časovou složitostí O(N3) a lineární paměťovou složitostí.
Je ale zřejmé, že takové řešení třináct bodů nezíská. Nyní si popíšeme řešení se složitostí O(N2 log N). Nebudeme zkoumat kružnice pro každé dva body, ale budeme zkoumat vždy všechny kružnice, na jejichž hranici je daný bod.
Vybereme tedy jeden ze zadaných bodů, kterému budeme říkat centrální, a budeme uvažovat kružnici, jejíž střed je o R nad daným bodem (kružnice tedy „stojí“ na tomto bodu). Pokud touto kružnicí budeme kolem daného bodu otáček tak, aby byl pořád na jejím okraji, budou ostatní body vstupovat a vystupovat z této kružnice. Stačí sledovat vstupující a vystupující body, upravovat si počet bodů v kružnici a po jedné otáčce kružnice kolem bodu si vybrat kružnici s maximálním počtem bodů uvnitř. Když tento postup provedeme pro všechny zadané body, získáme zajisté kružnici s největším počtem bodů uvnitř.
Mějme nějaký centrální bod. Polohu kružnice, která se ho dotýká, budeme určovat úhlem, který svírá spojnice středu kružnice a centrálního bodu s osou x. Řekněme, že pro daný centrální bod a další bod dokážeme zjistit úhly, kdy tento další bod vstoupí do kružnice, kterou rotujeme kolem centrálního bodu, a kdy z ní vystoupí. Pro všechny necentrální body získáme O(N) úhlů. Pokud tyto úhly setřídíme, můžeme pak v lineárním čase provést otáčení kružnice kolem centrálního bodu a najít tak kružnici s největším počtem bodů uvnitř. Pro jeden centrální bod bude tento postup trvat O(N log N) času kvůli třídění úhlů. Celkem tak získáme řešení v čase O(N2 log N) s lineární paměťovou složitostí.
Zbývá vyřešit několik detailů. Za prvé, pro jeden úhel je třeba zpracovat nejprve všechny vstupy a pak až výstupy bodů. Za druhé, v počáteční pozici kružnice musíme spočítat, které body jsou už uvnitř. Můžeme to provést triviálně v lineárním čase, protože to provádíme pro každý centrální bod jenom jednou. A za třetí, musíme umět spočítat úhel vstupu a výstupu bodu z kružnice. Mějme centrální bod c a jiný bod b, který je od něj vzdálený d ≤ 2R.
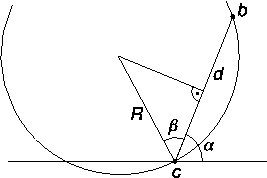
| d |
| 2 |
Program implementuje popsaný algoritmus s tím rozdílem, že kružnicí otáčí proti směru hodinových ručiček a body, které jsou na začátku v kružnici, poznává tak, že jejich úhel vstupu je větší než úhel výstupu.
20-5-4 Dračí chodbičky (Zadání)
Napřed, jak bude algoritmus fungovat. Nejdříve bude ignorovat veškeré jeskyně s pokladem a na tom zbytku spočítá minimální kostru, například algoritmem popsaným v kuchařce 18-3. Poté vezme každou jeskyni s pokladem a připojí ji k nejbližší jeskyni bez pokladu. Jediné na co si je třeba dát pozor je speciální případ, pouze dvě jeskyně, obě s pokladem.
Proč to funguje? Kdyby byly dvě jeskyně s pokladem spojeny napřímo a žádná další cesta z nich nevedla, pak utvoří zcela samostatnou komponentu. Tedy, každá taková musí být připojená k některé bez pokladu. Je jedno, ke které, neboť zbylé jeskyně musí být navzájem propojené (a lze nahlédnout, že přes jeskyně s pokladem to nelze). Tedy vybereme si tu, ke které vede nejkratší chodba.
Zbylý kus musí být navzájem propojený a mít minimální možný součet hran. Toto přesně počítá algoritmus minimální kostry a jeho zdůvodnění správnosti lze nalézt ve zmíněné kuchařce.
Zbývá ještě časová a paměťová složitost. Paměťová je jednoduchá, pamatujeme si každý vrchol (jeskyni) a hranu (chodbu), tedy O(N+M). V časové bude jednak figurovat tvorba minimální kostry, který je O(N+M· log M). Při připojování pokladů projdeme každý vrchol a každou hranu nejvýše jednou, tedy zde je složitost O(N+M). Celková bude tedy O(N+M· log M).
A jedna implementační poznámka na závěr. Obě fáze jsou na sobě zcela nezávislé. Proto je možné tyto dvě fáze prolnout a udělat je obě na jeden průchod seřazenými hranami, jen si u hran dáme pozor, aby maximálně jeden z konců byl s pokladem a nebyl již připojen jinam.
20-5-5 Roztržitý matematik (Zadání)
Milí řešitelé a řešitelky, podle výsledků praktické úložky, které právě nemohu najít, jste si všichni vedli skvěle. Nebo si alespoň myslím, že jste si vedli skvěle …tedy určitě alespoň většina z vás …
Každopádně jsem si tu pro vás připravil nástin řešení, abyste si udělali alespoň hrubou představu o tom, jak to u nás chodí a na co si dávat pozor. Na úvod bych rád zdůraznil, že s papíry se to nemá tak jednoduše, jak by se mohlo na první pohled zdát. Jakmile na papír cokoli napíšete, začne žít vlastním životem a sám od sebe se přesunuje. Má tendenci se schovávat pod jiné papíry, když ho právě potřebujete, a naopak ležet na vrchu a překážet, pokud zrovna hledáte něco jiného.
Ale to jsem trochu odbočil…ach ano – to řešení. Někde jsem ho tu měl připravené. Kam se asi mohlo schovat? V zásadě teď může být kdekoli. Věřili byste, že jsem jednou našel svůj článek dokonce až pod automatem na kávu? Opravdu netuším, jak se tam dostal, protože automat je na chodbě poměrně daleko od mého kabinetu …
Ale abych se vrátil – problém, se kterým se každý den potýkám, se nazývá move-to-front transformace. Můj kolega z informatiky tvrdí, že se používá také při kompresi, ale to mi příliš nepomůže. Jádro problému spočívá v rychlém nalezení a odebrání i-tého papíru v pořadí a jeho vložení na začátek tak, aby se správně posunuly ostatní papíry.
Půjdeme-li na to přímo, nenarazíme na žádné potíže. Všechny papíry si uložíme do pole tak, že i-tý papír se nachází na indexu i. Nalezení papíru máme zadarmo v konstantním čase. Papír odebereme a všechny papíry, které jsou před ním, posuneme o jednu pozici. Tím se nám vzniklá díra zaplní a naopak vytvoříme díru na první pozici. Nyní na začátek vložíme odebraný papír a máme hotovo.
Tohle řešení má lineární časovou složitost na každou operaci (tzn. celkem O(N ·k), kde N je počet papírů a k počet operací), takže se hodí k přerovnávání několika papírků na stole mého pořádkumilovného kolegy, ale prohledání celého mého kabinetu by zabralo věčnost …
Dlouho jsem si s tím lámal hlavu, až mi kolega informatik poradil lepší řešení. Jak jsem se dozvěděl, klíčem jsou stromy – tím nemyslím to, co mi roste pod okny, ale binární stromy. Je vhodné použít nějakou variantu vyvažovacích stromů (AVL, Červeno-černé, …), protože jinak vaše řešení rychle zdegeneruje na lineární spojový seznam. Sám se ve stromech příliš nevyznám, takže pokud vás zajímají detaily, nahlédněte do kuchařky.
V každém vrcholu u bude uložen počet prvků (označme jej c(u)) v podstromě, který má u jako kořen, a také číslo papíru, který je v tomto vrcholu uložen.
Takový strom postavíme jednoduše. Na začátku víme, že papíry jsou seřazeny od 1 do N. Kořen našeho stromu bude reprezentovat prostřední papír z daného intervalu. Levý a pravý podstrom pak vygenerujeme rekurzivně. Počet prvků v každém podstromě spočítáme také snadno: stačí v každém vrcholu sečíst:
Nyní se podívejme, jak rychle nalézt, co hledáme. Řekněme, že jsme ve vrcholu u a pátráme po i-tém papíru (oproti zadání je budeme číslovat od nuly, to vyjde elegantněji). Podíváme se na počet prvků v levém podstromě ℓ= c(<levý syn u>). Pokud je i < ℓ, víme, že se hledaný prvek nachází v levém podstromu, je-li i = ℓ, hledaným prvkem je u sám, a konečně v posledním případě (i > ℓ) se hledaný papír nachází v pravém stromu. Samozřejmě si musíme dát pozor, když přecházíme do pravého podstromu. Tam už nehledáme i-tý papír, ale papír s indexem i - ℓ- 1.
Odebrání samotného papíru pak probíhá podle pravidel mazaní z binárního vyhledávacího stromu (viz kuchařka a též níže). Stejně tak musíme po mazaní provést vyvážení stromu, které závisí na tom, jaký typ stromu jsme použili (opět viz kuchařka). Po mazání je nezbytné ještě opravit všechny hodnoty c(u) ve vrcholech, které ležely po cestě k hledanému papíru.
Odebraný papír vložíme do stromu na nejlevější pozici (tedy na první místo). Opět dodržíme pravidla pro vkládání do stromu, opravíme všechny hodnoty c(u) po cestě a provedeme vyvážení.
Nakonec potřebujeme ještě vypsat konečnou permutaci dokumentů. Stačí pouze projít a vypsat náš strom v pořadí in-order.
Časová složitost uvedeného algoritmu je O(log N) na jednu operaci, protože hledání, mazání i vkládání trvá u vyváženého binárního stromu logaritmicky dlouho. Paměťová složitost se nám přitom nezhoršila. Sice spotřebujeme několikrát víc paměti, ale asymptoticky zůstáváme stále na příjemné složitosti O(N).
Jeden student mi ještě tvrdil, že zná řešení v čase O(k √N), ale vůbec si nejsem jistý, jak by takové řešení mělo fungovat, takže si můžete zkusit takové řešení napsat za domácí cvičení.
Náš čas na konzultaci bohužel vypršel a já se s vámi musím rozloučit. Někde jsem tu měl papír se seznamem dalších schůzek – ale kam jsem si ho sakra založil …?
V programu si vyzkoušíme jednu méně tradiční, ale moc pěknou odrůdu stromů, totiž BB-α stromy již letmo zmíněné v kuchařce. Místo podle hloubky budou vyvažovány podle váhy, čili počtu vrcholů v podstromech. V dokonale vyváženém stromu platí, že se váha levého a pravého podstromu každého vrcholu liší nejvýše o jedničku. My nebudeme tak přísní: povolíme, aby jeden podstrom měl až dvakrát větší váhu než druhý.
Všimněte si, že toto pravidlo nám stále zaručuje logaritmickou hloubku: oba synové vrcholu s váhou w mají váhy nejvýše (2/3)w, jejich synové nejvýše (2/3)2w atd., takže váhy stále klesají exponenciálně. Hloubka stromu tedy bude přibližně log3/2 n.
Když do stromu přidáme nový vrchol, a nebo naopak nějaký smažeme, přepočítáme všechny váhy na cestě ze změněného vrcholu do kořene (všimněte si, že to tak jako tak v naší úloze potřebujeme). Přitom budeme kontrolovat, jestli váhy stále splňují vyvažovací podmínku. Jakmile objevíme vrchol, ve kterém podmínka neplatí, nebudeme se snažit vyvážení obnovit rotacemi (což by také šlo), ale podnikneme daleko razantnější krok: celý podstrom rozebereme a předěláme na dokonale vyvážený.
Přeskládání celého podstromu je samozřejmě časově náročné: trvá O(<váha podstromu>) – inu, když se kácí les, létají třísky –, ale ukážeme, že nebudeme „kácet“ příliš často, takže se nám složitost nepokazí.
Představme si na chvilku, že do stromu jenom vkládáme. Vyberme si nějaký podstrom a sledujme, co se s ním bude dít. Nejprve je během některého kácení postaven jako dokonale vyvážený a tehdy se váha jeho levého a pravého syna rovnají (±1) nějakému číslu w. Pak do podstromu přibývají nové prvky a vyvážení se postupně zhoršuje. Nakonec se situace stane příliš nahnutou, a tak podstrom pokácíme. Všimněte si, že mezi vytvořením podstromu a jeho pokácením se musel jeden syn stát dvakrát těžším než druhý, takže se muselo objevit alespoň w nových prvků. Přebudování samo trvá O(w), tudíž stačí, aby na něj každý z w nově vložených prvků přispěl časem O(1). Každý prvek si takto předplatí všechna pokácení na cestě z něj do kořene (přesně těm přispívá), a tak celkově přispěje časem O(log n).
Mazání nám tuto analýzu trochu zkomplikuje, ovšem snadno nahlédneme, že když je povoleno jak vkládat, tak mazat, nejrychlejší způsob, jak pokácet strom váhy 2w, je smazat z jednoho jeho podstromu w/2 vrcholů a druhý podstrom nechat na pokoji. (Na počátku měly podstromy váhy w, na konci má jeden w/2 a druhý stále w.) Opět na to potřebujeme řádově w operací, takže původní úvaha s příspěvkem O(log n) na operaci stále funguje.
Kolik času tedy spotřebujeme na jednu operaci? Inu, když máme smůlu a zrovna jsme způsobili jedno nebo více kácení, operace může trvat až n kroků. Ovšem díky našemu principu „předplácení si“ stále platí, že libovolných k po sobě jdoucích operací trvá O(k log n), což nám pro řešení úlohy úplně stačí. Tomu se obvykle říká, že každá operace má amortizovanou časovou složitost O(log n).
Stálo to trochu počítání, ale zato jsme si ušetřili spoustu programování. Inu, i informatici jsou líní a někdy i roztržití.
20-5-6 Hrady, hrádky, hradla (Zadání)
a) Jak se průběžná parita má chovat? Inu, pokud na vstupu
přijde nula, parita se nijak nemění. Pokud naopak přijde jednička,
parita se zneguje. Jinými slovy nová parita je xor staré parity
s bitem na vstupu. Pak už stačí přidat klopný obvod d, aby si
paritu pamatoval a novou zapsal při náběžné hraně hodinového
signálu.
Ještě bychom měli domyslet, jakou hodnotu má mít parita na začátku
výpočtu. Za tímto účelem doplníme klopný obvod d o vstup CLR
(clear), který způsobí jeho vynulování, a necháme na uživateli,
ať na začátku „zatahá za reset“ a obvod zinicializuje. (Takový
vstup mají i opravdové klopné obvody.)
Celý obvod bude tedy vypadat takto:
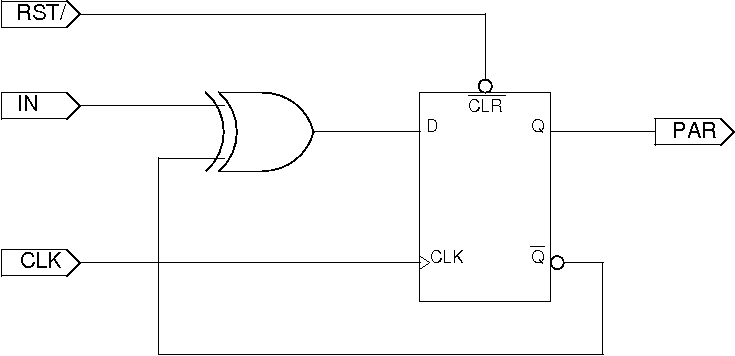
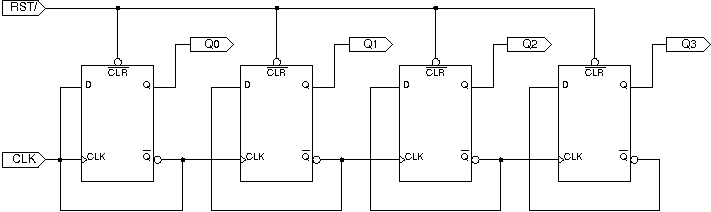
b) Ani čítač nebude složitý. Nejnižší bit dvojkového čítače při každém „tiku“ hodin svou hodnotu zneguje, jinými slovy na jeho spočítání stačí dělička frekvence zmíněná v zadání. Další bit v pořadí se změní právě tehdy, když nejnižší bit přejde z jedničky do nuly, čili když nastane náběžná hrana na negovaném výstupu zmíněné děličky. Takže stačí na tento negovaný výstup napojit další děličku, a tak dále.
Obvod pro N-bitový čítač tedy bude sestávat z N klopných obvodů d
zapojených jako děličky. Schéma pro N=4 najdete níže, sem do úzkého
sloupečku se nevešlo.
Zbývá dodat snad jen to, že i u obvodů tohoto druhu má smysl zkoumat
časovou složitost – v tomto případě dobu, za kterou se obvod po tiku
hodinového signálu ustálí a vydá stabilní výstup. U našeho čítače
je to O(N) kroků (změna musí „probublat“ až N d-čky).
Šel by ale postavit i tak, aby reagoval už za O(log N) kroků,
zkuste si to třeba o prázdninách vymyslet. S páječkou v ruce se
s vámi loučí