Druhá série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 24-2-1: Požární poplach
- 24-2-2: Centrální sklad
- 24-2-3: Odčítání
- 24-2-4: Odbočení vlevo
- 24-2-5: Logická formule
- 24-2-6: Závorky
- 24-2-7: Štětcování
- 24-2-8: Alfa-beta ořezávání a piškvorky
24-2-1 Požární poplach (Zadání)
Uvedieme tri postupne zlepšujúce sa riešenia. Prakticky všetky riešenia, ktoré prišli a boli správne, popisovali jeden z nižšie uvedených algoritmov.
Aby sme nezapísali viac, ako je treba, je dobré si všimnúť čo majú všetky algoritmy riešiace túto úlohu spoločné. A síce je nutné zistiť, kedy jednotlivé stromy (políčka 1×1 označené bodkou) začnú horieť. Keby sme túto informáciu nemali, tak o ľubovoľnej ceste lesom zľava doprava nie sme schopní rozhodnúť, ako dlho bude priechodná. Potrebné zistíme prehľadávaním do šírky od políčok, ktoré sú označené ako ohne. Časová zložitosť je lineárna k veľkosti lesa, teda O(R · S).
Drevorubačský algoritmus
Myšlienka je pokúsiť sa po označení nejakého políčka (viď predchádzajúce odstavce) nájsť cestu lesom zľava doprava (napr. opäť prehľadávaním do šírky).
Predstavme si, že sme nejaké políčko označili číslom i a nevieme nájsť cestu (po neoznačených políčkach – tie ěste nehoria) zľava doprava. To teda znamená, že les je priechodný najneskôr v čase i-1.
Algoritmus funguje, avšak má nepeknú časovú zložitosť. Označených políčok je R · S a pre každé takéto políčko raz prehľadáme do šírky celý les. Teda celková časová zložitosť tohoto algoritmu je O(R · S · R · S) = O(R2 · S2), teda kvadratická k veľkosti lesa.
Zlepšujeme binárnym vyhľadávaním
Predpokladajme, že les dohorel v čase n (políčka máme označené číslami 0…n).
Jednoduchým pozorovaním je, že ak je les v čase k priechodný, tak je určite priechodný aj v čase menšom ako k. Podobne ak je les už v čase k nepriechodný, tak neskôr priechodný určite nebude. Keď teda zvolíme nejaké k a skúsime nájsť cestu po políčkach označených číslom väčším ako k, tak podľa výsledku (buď sme našli cestu alebo nenašli) nás nemusia viac zaujímať políčka označené číslom väčším (ak sme cestu nenašli) alebo menším (ak sme cestu našli).
Z tohoto pozorovania nás môže napadnúť použiť binárne vyhľadávanie. Nech d = 0 a h = n + 1. Opakujeme nasledovné:
- pozrieme sa či vieme prejsť lesom v čase ⌊(d + h) / 2⌋
- ak vieme, tak položíme d = (d + h) / 2
- inak h = (d + h) / 2
- ak h - d = 1, tak skončíme, výsledok je d
Nahliadnime ešte, že d je hľadané číslo. Predtým, než sme skončili, sme buď znížili h na d + 1, alebo zvýšili d na h - 1. V prvom prípade to znamená, že v čase d + 1 sa prejsť nepodarilo, ale zároveň vieme, že v čase d a menšom prejsť vieme, teda správna odpoveď je d. Druhý prípad si analogicky rozmyslíte sami.
Zostáva už len rozobrať časovú zložitosť. Binárne vyhľadávanie zaberie O(log n) krokov, kde n = O(R · S). Každý krok má časovú zložitosť O(R · S), preto výsledná časová zložitosť druhého algoritmu je O(R · S · log n).
A konečne lineárne riešenie
Opäť predpokladajme, že máme označené políčka číslami 0…n. Chceme odpozorovať, či je les priechodný v čase k, ale nie len tak bez rozmyslu, pretože to by sme sa dostali časovú zložitosť O(R · S · n) a boli by sme niekde medzi dvoma vyššie uvedenými algoritmami. Budeme chcieť na každé políčko stúpiť O(1)-krát a tým pádom dosiahnuť časovú zložitosť O(R · S).
Môžeme to spraviť napríklad tak, že budeme postupovat v čase dozadu a prepočítavať, z ktorých políčok je dosiahnutelný cieľ. Pre čas k pridáme políčka, ktoré začali horieť v čase k. Ak z nejakého pridaného políčka existuje cesta na pravý okraj, tak z tohoto políčka prehľadáme do širky celý les ale len po pridaných políčkach. Všetky políčka, na ktoré pri prehľadávaní stúpime uzavrieme (pri ďalšom prehľadávaní sa už na ne nedostaneme). Ak sme uzavreli aj nejaké políčko na ľavom okraji, tak môžeme skončiť.
Políčka budeme označovať U – uzavreté, O – otvorené a X
budú ostatné. Pre i = n, …, 1 budeme opakovať:
- všetky políčka označené číslom i označ ako
O - ak existuje políčko P, ktoré je označené
Oa susedí s políčkom označenýmUalebo je napravo, tak P označUa spusti z P prehľadávanie do šírky po políčkach označenýchOa všetky označU - skonči hneď, ako je nejaké políčko naľavo označené
U– výsledok je i
Nech k je číslo, ktoré hľadáme. Potom v k-tom sú políčka s číslom k a
väčším označené U alebo O a nutne musí existovať cesta po týchto
políčkach zľava doprava a nájdeme ju prehľadávaním do šírky. V čase k+1 ešte
nemohla, inak by sme ju našli už vtedy.
Každé políčko najprv označíme O a ak sa k nemu dostaneme znovu, tak ho
označíme U a potom ho už viac neuvidíme. Celková časová zložitosť teda je
O(R · S).
Pamäťová zložitosť všetkých troch popísaných algoritmov je O(R · S).
24-2-2 Centrální sklad (Zadání)
Centrální sklad byl tak jednoduchý, jak jen vypadal. Kdo se nebál řešit praktickou úlohu, tak měl k plnému počtu bodů velice blízko.
Nejprve se zamyslíme nad definicí průměrné vzdálenosti. Ta praví, že průměrná vzdálenost je součet vzdáleností ke všem výrobcům vydělená jejich počtem. Počet výrobců je stále stejný, dělení počtem výrobců tedy nemění výsledek a můžeme ho zanedbat.
Nyní tedy už počítáme jen součet vzdáleností. Představme si nyní, že bychom chtěli centrální sklad postavit na některém místě tak, že nalevo od něj by byli dva výrobci a napravo od něj tři výrobci. Vyplatí se to? Nevyplatí. Představme si, že ho posuneme o malé číslo c doprava. Vzdálenost od výrobců nalevo bude o c větší, čímž součet zvětšíme o 2c, ale zároveň ho o 3c snížíme díky menší vzdálenosti od výrobců napravo. Tedy jsme si polepšili.
Jak dlouho budeme moci takto zlepšovat? Dokud stále ještě na jedné straně bude víc výrobců, než na straně druhé. Pro lichý počet výrobců je tedy řešení unikátní – postavit sklad přesně na umístění prostředního výrobce (mediánu) – a pro sudý počet výrobců si můžeme vybrat libovolné místo mezi ⌊n/2 ⌋-tým výrobcem a ⌈n/2⌉-tým výrobcem.
Neměli jste tedy vymyslet nic jiného, než jak najít medián v nesetříděné posloupnosti. Optimální algoritmus pracuje v lineárním čase a je popsán v naší kuchařce Rozděl a panuj; my jsme však dovolili i nalezení mediánu pomocí setřídění posloupnosti některým rychlým algoritmem, jako například QuickSortem.
24-2-3 Odčítání (Zadání)
Program funguje korektně v případě, kdy je menšitel menší nebo roven menšenci
a první platná cifra menšence je uložena v prvni[0]. Jak funkce odčítá?
Nejdříve si uvědomme, co se děje v první části algoritmu. Na i-tou pozici
v poli vysledek ukládáme rozdíl hodnot prvního a druhého čísla zvětšený
o devět. Nakonec přičítáme k poslednímu prvku jedničku. Skutečný rozdíl je tedy
zvětšený o číslo 10d (kde d je délka pole vysledek). Navíc máme tento
výsledek uložený v upravené desítkové soustavě, v níž mají jednotlivé řády
váhy 10i, ale číslice mohou být libovolné nezáporné (ne jen 0–9).
V druhé části algoritmu pak čísla v poli vysledek normalizujeme do
klasického desítkového zápisu a zároveň se zbavujeme přebytečného 10d. To se
děje tak, že kontrolujeme, zda je na i-té pozici v poli číslo větší než 10.
Pokud ano, odečteme desítku a předáme ji jako jedničku do vyššího řádu, čímž
upravíme prvky v poli vysledek tak, abychom měli v každém prvku pole vždy
jen jednociferné číslo. Všimněme si dále, že při předání jedničky doleva u prvku
pole s indexem 0 odčítáme od výsledku přebytečné 10d.
Nyní ke složitosti. Paměťová je zjevně lineární (třikrát pole velikosti d a konstantní počet proměnných k tomu). Časová je taktéž lineární. V první fázi algoritmu provádíme d operací. V druhé části při každém kroku doleva klesne součet všech číslic, zatímco při kroku doprava se nezmění. Proto je celkový počet kroků doleva nejvýš lineární; kroků doprava pak je nejvýše o d víc než kroků doleva, takže také lineárně.
24-2-4 Odbočení vlevo (Zadání)
Kdo už slyšel o teorii grafů, tak si jistě pamatuje, že síť křižovatek a cest je nejlépe modelovaná právě pomocí grafu – a pro hledání nejkratší cesty v grafech máme lineární algoritmus procházení do šířky, také zvaný BFS.
Kdo o BFS nebo grafech ještě nic neví, ten si může doplnit znalosti v našich kuchařkách.
Nejsme ale zcela hotovi – musíme totiž postavit ze zadání vhodný graf, abychom mohli spustit BFS. Kdybychom jen prohlásili křižovatky za vrcholy a ulice za hrany, narazili bychom, protože podmínka v zadání (můžeme jet jen rovně nebo doprava) nám říká, že některé ulice nesmí být průjezdné z některých křižovatek.
Můžeme tedy z neorientovaných grafů přejít na grafy orientované – takové, kde každá hrana má i směr, kterým ji lze procestovat. BFS funguje stejně dobře i v takovýchto grafech.
Nicméně ani teď ještě nejsme hotovi, protože ono docela hodně záleží na tom, ze kterého směru přijíždíme. Když přijíždíme na křižovatku z jihu, můžeme jet rovně na sever nebo doprava na východ – jenže když jedeme z východu, můžeme pokračovat rovně na západ nebo doprava na sever.
Jinými slovy, kdybychom měli vrcholy jako křižovatky, tak by se hrany musely měnit podle toho, jak do křižovatky přijedeme. Grafy se ale takto měnit nesmí. Zkusme vytvořit graf jinak.
My si uvědomíme, že když jedeme ulicí v jednom směru, už je naprosto jednoznačné, jaké máme možnosti na další křižovatce. Mohli bychom tedy vytvořit graf tak, že vrcholy tohoto grafu jsou ulice z našeho zadání a orientované hrany povedou mezi ulicemi U a V, pokud z ulice U na další křižovatce jde odbočit podle pravidel do ulice V.
Na další křižovatce… ale která je další? Ulice U je ohraničena dvěma křižovatkami, ale pro každou z nich budou hrany jiné – proto budeme mít dva vrcholy pro každou ulici, podle toho, jedeme-li jedním směrem nebo tím opačným.
Jakmile máme danou ulici a směr, už je jasné, která je další křižovatka a tedy i kam dál povedou hrany.
Na tento „graf orientovaných ulic“ už můžeme pustit procházení do šířky a najít nejkratší cestu v lineárním čase. Jen ještě musíme poznamenat, že nyní umíme vyhledat jen nejkratší cestu mezi orientovanými ulicemi, ne křižovatkami – ale protože z každé křižovatky vedou jen čtyři ulice, můžeme prostě náš algoritmus zavolat pro každou možnou ulici vedoucí ze startu a pro každou možnou ulici vedoucí do cíle. Nejvýše ho tedy můžeme pustit 16krát, a jak známo, konstanta nám složitost algoritmu nijak podstatně nezhorší. (Jen konstantně.)
Na závěr ověříme, že jsme naší konstrukcí nevytvořili příliš velký graf. Na začátku máme N křižovatek, mezi nimi je nataženo nejvýše 4 · N ulic. My jsme vytvořili méně než 8 · N vrcholů, za každou ulici a směr jeden. Kolik náš graf má hran? No, na každé křižovatce máme dokonce už jen dvě možnosti, jak jet dál – tedy jich bude mít nejvýše 16 · N, a to je stále jen lineární zvětšení.
Převést vstupní mapu na náš graf lze také udělat v lineárním čase (pokud dostaneme vstupní data v rozumném formátu, což jste mohli předpokládat).
Sečteno a podtrženo – vstup zvětšíme jen konstanta-krát, pak na něj zavoláme lineární kuchařkový algoritmus (nejvýš 16krát) a naše časová i paměťová složitost tedy bude lineární.
24-2-5 Logická formule (Zadání)
Držme se zásad známého hesla rozděl a panuj. Budeme výraz postupně rozkládat na stále menší podvýrazy, dokud je nedokážeme triviálně spočítat.
Představme si, že již máme dva podvýrazy, u kterých známe počty pravdivých uzávorkování a celkové počty korektních uzávorkování. Počty pravdivých uzávorkování si označme Pa a Pb a celkové počty uzávorkování Ca a Cb. Celkový počet uzávorkování výrazu spočteme jednoduše jako Ca · Cb, protože můžeme skombinovat jakákoliv dvě korektní uzávorkování podvýrazů.
Pokud je mezi podvýrazy operátor and, je počet pravdivých uzávorkování celého výrazu roven Pa · Pb (protože celý výraz bude pravdivý v případech, kdy budou pravdivé oba jeho podvýrazy).
Pokud je mezi podvýrazy operátor or, je to již zajímavější. Celý výraz bude pravdivý v případech, kdy je pravdivý pouze levý podvýraz, pouze pravý podvýraz nebo když jsou pravdivé oba.
Když je pravdivý levý podvýraz, může být pravý podvýraz jakkoliv korektně uzávorkovaný, tedy dostáváme Pa · Cb pravdivých uzávorkování. Obdobně pro případ, kdy je pravdivý pravý podvýraz.
Tím jsme ale dvakrát započítali i případy, kdy jsou pravdivé oba podvýrazy, musíme proto ještě odečíst Pa · Pb (podle principu inkluze a exkluze). Celý vztah pro operátor or je tedy Pa · Cb+Pb · Ca-Pa · Pb.
Teď, když už máme definované skládání podvýrazů, můžeme přistoupit k samotnému počítání. Základním přístupem je rozdělit celý výraz na podvýrazy a podle postupu popsaného výše spočítat počet pravdivých uzávorkování.
Vždy vezmeme celý výraz a postupně ho rozdělíme ve všech logických operátorech. Pro každý operátor rekurzivně spočítáme počty pravdivých a všech korektních uzávorkování příslušných podvýrazů a podle vztahů pro and a or určíme počty uzávorkování při rozdělení v tomto logickém operátoru.
Rekurze se zastaví v okamžiku, kdy dojde k jednoprvkovým podvýrazům (v tom okamžiku vrátí jejich hodnotu). Po spočtení hodnot ve všech operátorech výrazu jenom posčítáme tyto hodnoty a získáme počty uzávorkování celého výrazu.
Lehce si ale všimneme, že spoustu věcí počítáme v rekurzi stále dokola. Nebylo by lepší si je pamatovat? Pro tento přístup ve stylu dynamického programování si tedy založíme dvourozměrné pole, ve kterém budeme ukládat vypočtené hodnoty pro podvýrazy začínající a končící na daných prvcích.
Vždy, když budeme chtít znát počet pravdivých uzávorkování daného výrazu, tak se nejdříve podíváme do tohoto pole a teprve poté případně rekurzivně spočítáme. A naopak, vždy, když vypočteme počet pravdivých a všech korektních uzávorkování u nějakého podvýrazu, uložíme si tyto hodnoty do pole.
Tím jsme si časově hodně pomohli. Podvýrazů je N2 s tím, že výpočet podvýrazů na jedné hladině (podvýrazů o stejné délce) nám v případě znalosti všech kratších podvýrazů trvá O(N). Díky tomu, že každý podvýraz počítáme pouze jednou, je celková časová složitost O(N3).
Paměťová složitost je kvůli použití dvourozměrného pole O(N2).
Ještě poznámka na konec: Počet korektních uzávorkování nějakého výrazu je n-té Catalanovo číslo. To je definováno jako
| 1 |
| n+1 |
| ( | 2n | ) |
| n |
Neudává pouze počet korektních uzávorkování, ale uplatnění najde i ve spoustě jiných úloh z kombinatoriky. Více informací lze najít například na Wikipedii.
24-2-6 Závorky (Zadání)
Většina z vás si správně uvědomila, že aby byla posloupnost správně uzávorkovaná, musí být počet levých závorek větší nebo roven počtu pravých ve všech prefixech a celkově počet levých a pravých závorek musí být stejný.
Nechť a je posloupnost závorek.
Zavedeme si pro ni dvě proměnné:
a.potrebujeme bude udávat počet levých závorek, který je potřeba napsat
před posloupnost, aby nikdy nebylo více pravých než levých závorek.
V a.navic je napsáno o kolik je v a více levých závorek než pravých.
Např. "())(".potrebujeme = 1,"())()".navic = -1
Posloupnost závorek a je správně uzávorkovaná, právě když
a.potrebujeme = 0 a zároveň a.navic = 0. Problém se tedy
redukuje na zjištění těchto dvou proměnných. Ale jak na ně přijít? Pokud bychom
znali dvě poloviny posloupnosti a a b, tak vypočítat proměnné pro jejich
spojení c už je rychlé.
Jaký je v c rozdíl počtů levých a pravých závorek, se spočítá jednoduše:
c.navic = a.navic + b.navic.
Kolik je potřeba doplnit závorek před c (c.potrebujeme), nemusí být
stejné jako a.potrebujeme, například když je a správně uzávorkované a
b.potrebujeme > 0.
Začátek posloupnosti b ovlivňuje hodnota a.navic a závorky, jež se mají
přidat před c, dokáží ovlivnit obě části c, takže platí, že
c.potrebujeme je maximum z a.potrebujeme
a b.potrebujeme - a.navic.
Pro triviální řetězce je "(".potrebujeme = 0, "(".navic = 1,
")".potrebujeme = 1, ")".navic = -1.
Můžeme tedy tyto proměnné určit pro triviální řetězce a spojováním
se dostat až k řetězci délky N.
Teď přijde trik: většina proměnných je po otočení stejná jako před ním, a tak není potřeba počítat vždy všechny. Když si nad řetězcem postavíme binární strom, tak bude stačit změnit jen vrcholy nad pozicí, kde se otáčela závorka. Čili bude potřeba O(log(N)) přepočítání proměnných a poté se podívat do kořene, jestli je posloupnost správně uzávorkovaná.
Na začátku potřebujeme O(N) času na vytvoření toho binárního stromu, poté nám na dotaz stačí O(log N) času. Paměťová složitost je O(N) kvůli uložení stromu.
24-2-7 Štětcování (Zadání)
Tato úloha se projevila jako dosti zrádná. Většinou jste ji řešili tak, že jste si našli všechny vodorovné a svislé vybarvené úseky, z jejich délek vybrali minimum a to prohlásili za výsledek. Bohužel toto řešení nefunguje například na tomto vstupu:
11000
11100
00111
00011
Minimální souvislý vodorovný/svislý úsek má velikost dva, zatímco obrázek dokážeme nakreslit pouze štětcem velkým jedna.
Když jsem mluvil o zrádnosti úlohy, tak jsem to myslel vážně. Nikdo úlohu nevyřešil úplně správně a i já jsem měl ve svém původním řešení chybu. Jak to tedy mělo být?
Ukážeme si jedno řešení pomocí binárního vyhledávání a jedno lineární řešení.
Všimneme si, že pokud obrázek umíme vybarvit štětcem velkým K, tak jej umíme vybarvit i libovolným menším štětcem. Když tedy zvládneme v rozumném čase ověřit, zda lze obrázek vybarvit daným štětcem, můžeme správnou velikost binárně vyhledat.
Nejdříve si pro každé políčko spočítáme, kolik je ve sloupci pod ním černých políček. To zvládneme v čase O(R · S). Dále si během výpočtu budeme pro každé políčko udržovat hodnotu H, jestli jsme toto políčko již vybarvili. Nyní pojedeme postupně po řádcích (budeme přikládat horní stranu štětce) a vždy, když budeme na místě, kde můžeme barvit, tak obarvíme všechna zatím neobarvená políčka a označíme je v H. Detaily výpočtu a jak postupovat při barvení, abychom si nepokazili časovou složitost, si můžete rozmyslet sami jako cvičení.
Každé políčko jsme obarvili maximálně jednou a zkusili jsme O(R · S) pozic štětce, tedy tento krok zvládneme dohromady v O(R · S). Společně s binárním vyhledáváním dostaneme časovou složitost O(R · S · log min(R, S)).
Nyní k lineárnímu řešení. My vlastně pro každé políčko chceme zjistit, v jakém největším čtverci leží. Pak z těchto hodnot vybereme minimum a dostaneme správné řešení. Jak na to? Nejdříve předvedu algoritmus, který úlohu řeší, a pak dokážu, že odpovídá správně.
Odteď budeme černá políčka nazývat jedničkami a bílá políčka nulami. Spočítáme, v jakém největším čtverci jedniček se jedničky nachází. Ovšem maximální čtverce budeme hledat jen pro ty jedničky, které mají vedle sebe alespoň jednu nulu. (Kraj považujeme za nulu.) U takových jedniček totiž dokážeme jednoduše určit, kterým směrem jejich čtverec povede.
Nyní bychom u každé jedničky chtěli znát, jak dlouhý souvislý úsek jedniček z ní vede směrem doprava, doleva, nahoru i dolů. To vše si dokážeme předpočítat v čase O(R · S). Pak pro danou krajní jedničku použijeme následující postup:
Jednička má alespoň z jedné strany nulu, BÚNO (BÚNO = bez újmy na obecnosti) vlevo. Nyní se od této jedničky vydáme směrem doprava, budeme se koukat na délky horních a spodních úseků jedniček a udržovat jejich minima Hmin a Dmin. Půjdeme směrem doprava, dokud nenarazíme na nulu a dokud Hmin + Dmin -1 ≥ K, kde K je počet kroků, které jsme udělali. Jinými slovy zvětšujeme náš čtverec tak dlouho, dokud to jde.
Není těžké nahlédnout, že jsme našli největší čtverec, ve kterém naše jednička leží. Pokud tento postup uděláme pro všechny krajní jedničky a z výsledků vybereme minimum, tak dostaneme maximální velikost štětce. Tento postup má časovou složitost O(R · S), protože jsme na každou jedničku obrázku přišli maximálně ze čtyř směrů.
Zbývá jen nahlédnout, že nám výsledek nemůže pokazit žádná jednička, která má za sousedy jen jedničky.
Pro takovou jedničku j uvažme největší čtverec, ve kterém leží. Takový čtverec určitě musí dvěma protějšími stranami sousedit s nulou, protože jinak bychom jej mohli zvětšit. Nyní se podíváme, jak se algoritmus choval u jedniček, které jsou ve čtverci vedle jedné z těchto dvou nul.
Pokud alespoň u jedné z nich najdeme právě takto velký čtverec, tak jsme vyhráli. Pokud ne, tak buď v jednom z těchto čtverců leží jednička j, nebo jeden z nich můžeme pošoupnout tak, aby v něm jednička j ležela. V obou případech dostáváme spor s tím, že jsme na začátku měli největší možný čtverec pro jedničku j.
Tím je řešení hotové. Vzorová implementace:
24-2-8 Alfa-beta ořezávání a piškvorky (Zadání)
Úkol 1: čtyři v řadě
Nebylo těžké si tipnout, že v piškvorkách, kde vyhrává řada čtyř značek, na neomezeném hracím plánu vyhrává začínající hráč (křížek). Důkaz rozborem případů není ani moc dlouhý, bylo však třeba dát si pozor a nezkrátit ho moc.
Největším chytákem úkolu bylo, že druhý hráč při obraně může vytvořit vlastní řadu dvou značek (tzv. dvojici) a pak se bude muset i první bránit, což někteří řešitelé opomněli zohlednit.
Pojďme tedy na rozbor případů, který se pokusíme co nejvíce zkrátit, aniž bychom něco zanedbali.
Klasickým trikem, jak v teorii her zredukovat počet probíraných případů, jsou symetrie. Když lze nějakou pozici získat z jiné pozice například otočením herního plánu nebo zrcadlením přes libovolnou osu a otočení či zrcadlení nemá v dané hře vliv na strategii hráčů, můžeme zkoumat obě pozice současně.
Jelikož hra je vyhraná pro prvního hráče, pro ověření jeho výhry si stačí pro tohoto hráče vždy vybrat nějaký tah, díky čemuž lze strom hry opět zmenšit (v úrovních prvního hráče). Je však třeba prozkoumat všechny protitahy soupeře.
Snadno si lze všimnout, že kdo udělá tři piškvorky v řadě s volnými políčky na obou koncích, vyhrál, nemá-li zrovna soupeř podobnou řadu. Taktéž vyhraje ten, kdo udělá najednou dvě dvojice, které obě mají volná políčka na koncích – za předpokladu, že soupeř nemůže dalším tahem udělat trojici s volnými konci.
Křížek táhne libovolně a kolečko má následně až na otočení herní plochy tři možnosti: zahrát vpravo od křížku (dotýká se ho hranou), nebo vpravo nahoře (dotýká se rohem) anebo někam mimo (tak, aby se kolečko nedotýkalo křížku).
Zahraje-li kolečko mimo křížek, udělá první hráč dvojici nedotýkající se kolečka. Druhý pak musí dvojici blokovat a v některých případech ještě může zahrozit, že vytvoří trojici s volnými konci:
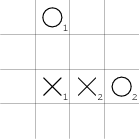
Křížek však takovou hrozbu dokáže odvrátit (což si není těžké rozmyslet) a navíc vždy udělá najednou dvě dvojice s volnými konci, čímž vyhrává.
Zahraje-li kolečko vpravo od křížku, první hráč umístí další značku pod kolečko. Nyní druhý musí blokovat dvojici, aniž by si mohl vytvořit vlastní dvojici (viz obrázek). Křížek dalším tahem vytvoří dvě dvojice s volnými konci a opět vyhrává.
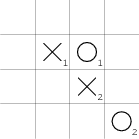
Poslední případ, v němž první kolečko sousedí rohem s křížkem, je zajímavý tím, že pro křížek je pak výhodnější zahrát tah nesousedící s prvním křížkem do situace na obrázku:
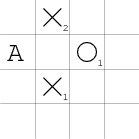
Kolečko musí nějak blokovat vznik trojice s volnými konci, přičemž má tři možnosti: nad ní, doprostřed (tím vytvoří vlastní dvojici) a pod ní.
V každém případě může křížek zahrát na políčko A, udělat dvě dvojice s volnými konci (případně ještě blokovat dvojici koleček), díky čemuž následně vyhraje.
Rozbor případů je hotov, takže nyní víte, jak za prvního hráče vyhrát, ať už bude soupeř vyvádět cokoliv (samozřejmě v rámci pravidel).
Úkol 2: devět v řadě
Zdůvodnění, proč má druhý neprohrávající strategii ve hře devět v řadě na neomezeném plánu, si skutečně zasloužilo svých 9 bodů i s nápovědou – správně ho měl jen jeden řešitel. Ukažme si tedy, jak bylo možné se s úlohou poprat.Nápověda byla rozdělení párů (dvojic), čemuž se říká párování. Správným řešením bylo vytvořit je tak, aby každá možná řada devíti značek obsahovala nějakou dvojici a každé políčko bylo maximálně v jedné dvojici (v našem řešení bude každé políčko přesně v jedné dvojici).
Než si ukážeme vytvoření oněch dvojic, popíšeme tzv. párovací strategii pro druhého hráče, díky níž neprohraje. Druhý vždy reaguje na předchozí tah prvního hráče tak, že zahraje do druhého políčka dvojice, do níž zahrál první hráč.
Tak je zajištěno, že po tahu druhého hráče bude každá dvojice z párování buď prázdná, nebo v ní bude kolečko a křížek. Díky tomu se nikdy nestane, že by v nějaké dvojici byly dvě stejné značky, takže nikdo nemůže dosáhnout řady devíti značek, jelikož každá taková řada obsahuje nějakou dvojici.
Jako rozdělení do dvojic si předvedeme Hales-Jewettovo párování. Obrázek vydá za tisíc slov, což v tomto případě platí dvojnásob – viz poslední stranu letáku.
Tento vzor se pořád opakuje, takže každé políčko herního plánu je v nějaké dvojici. Snadno lze ověřit, že každá možná řada devíti políček obsahuje nějaký pár.
Mimochodem, bylo možné si všimnout, že pokud je remízová varianta piškvorek, v níž vyhrává osm v řadě, musí být remíza i devět v řadě. Jenže o osmi v řadě jsme se jen letmo zmínili, bylo tedy třeba dokázat, že osm v řadě je remíza, což není vůbec, ale vůbec jednoduché.
Pokud vás piškvorky zajímají, můžete se na různé varianty a jejich výsledek podívat na internet.
