První série dvacátého devátého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu pošleme každému, kdo vyřeší tři libovolné úlohy na plný počet bodů.
Zadání úloh
„Nepovídej mi, že máme zase místo placek chlebové uhlí!“ poznamenal naoko
výhružně Warin a poklepal si na meč zavěšený za pasem. Samozřejmě to nemyslel
vážně, ale s Rheou se rádi navzájem škádlili. Znal se s ní déle než s kýmkoliv
jiným z jejich malé družinky a prožili toho spolu již hodně – on jako rytíř
řádu, ona jako nadaná kouzelnice.
Zbytek jejich družiny nacházející se v severské pustině tvořili ještě
nadaný zloděj a lukostřelec Gorf a druhý rytíř, mladý Lian. Do této prapodivné
skupinky je svedl důležitý úkol a už více než týden putovali daleko za známými
a bezpečnými cestami království.
Teď ale byl jejich hlavní starostí ukrutný hlad. Připálené placky sice nejsou
zrovna lahůdka, ale když se z nepřipálené strany namažou máslem, tak se jíst
dají. Jenom při rychlém sundavání z ohně je Rhea poskládala náhodně na jednu
hromádku.
 29-1-1 Připálené placky (8 bodů)
29-1-1 Připálené placky (8 bodů)
Máme na sobě položenou spoustu placek, každá z nich je z jedné strany připálená
a z druhé strany krásně dozlatova. Rádi bychom všechny placky otočili
nepřipálenou stranou nahoru, abychom je pak mohli všechny rychle namazat máslem.
Bohužel placky jsou ještě příliš horké na to, abychom je brali do rukou.
Jediné, co můžeme dělat, je podebrat si několik vrchních placek pánvičkou a celou
tuto část otočit. Jak to vypadá, si můžete prohlédnout na následujícím obrázku.
Dostanete zadáno, jak vypadá hromada placek (posloupnost říkající, které
z placek leží nahoru připálenou stranou a které nepřipálenou). Vaším úkolem je
najít co nejkratší posloupnost podebrání a otočení takovou, aby se po jejím
provedení všechny placky nacházely nepřipálenou stranou nahoru.
Řešení
Další den ráno uklidila družina chvatně své ležení a vydala se dál k úbočí
kopce, který se před nimi rýsoval. Nacházelo se zde jedno z těch samostatných
měst vzdorujících místní divočině a občasným nájezdům goblinů. Tohle vypadalo,
že i docela prosperuje.
Protože jim docházely zásoby a navíc potřebovali zjistit nějaké informace,
vydal se Warin s ostatními k městské bráně. Warin s Lianem schovali svá
brnění do nenápadných ranců na nákladním mezku a štíty se symboly řádu zakryli
plátnem. Bezpečnější bylo tvářit se jako nějací náhodní dobrodruzi.
Když u městské brány uplatili strážného dvěma zlaťáky vtisknutými do dlaně,
nemuseli ani odpovídat na žádné otázky a byli vpuštěni dovnitř. Po přiblížení se
k tržišti se ale družinka stala svědky nějaké hádky. Skupina místních
kupců se dohadovala, kdo má komu co zaplatit. Rhea se rozhodla, že se mezi ně
vetře, zkusí jim poradit a přitom získat nějaké informace.
 29-1-2 Kupecké počty (11 bodů)
29-1-2 Kupecké počty (11 bodů)
Skupina kupců se společně podílela na jedné velké investici. Každý
platil nějakou část, některé z nich to stálo více a některé naopak méně. Nyní by
si chtěli všechny náklady rovnoměrně rozdělit tak, aby ve výsledku investovali
všichni stejně.
Kupci se mohou vyrovnat tím, že ti, kteří platili málo, dají nějaký obnos
těm, kteří platili hodně. O každém předání peněz se ovšem musejí dělat záznamy
v účetních knihách, a tak by kupci chtěli provést těchto převodů peněz co možná
nejméně.
Navíc se ale žádný z kupců nechce zadlužit více, než už je, nebo se naopak
nechat přeplatit víc, než už přeplacený je. Není tak třeba možné kupci, který
má dostat 100 zlatých, dát 120 zlatých, protože by se tím stal o 20 zlatých
přeplacený. Stejně tak není možné poslat jakékoliv peníze kupci, který ostatním
dluží (zadlužil by se ještě víc).
Vymyslete postup, který pro zadané částky zaplacené jednotlivými kupci spočítá,
kdo komu má kolik dát tak, aby byla respektována uvedená pravidla a převodů bylo
málo.
Spočítat řešení s úplně nejmenších počtem převodů je těžký problém a tak to po
vás ani nechceme (jako dobrovolné cvičení si však můžete zkusit rozmyslet, proč
je to těžký problém). K vyřešení úlohy stačí, když vymyslíte postup vedoucí
k maximálně dvojnásobnému počtu převodů peněz, než je optimum. Důležitou částí
je i důkaz, že uděláte nejvýše dvojnásobek převodů, než je nezbytně nutné udělat.
Řešení
Rhea se rychle prodrala davem a využila svého přirozeného půvabu k tomu, aby si
od kupců získala pozornost. Tu prohodila nějaké slovo, jinde poradila
a kupci se rychle dostali k vzájemné dohodě.
Za necelých dvacet minut se Rhea opět vynořila u zbytku skupinky a vítězoslavně
zahlásila: „To byla hračka, to mě bavilo. Od tamtoho obchodníka s kožešinami
jsem se dozvěděla, kdo by mohl vědět víc o té potvoře. Je to stopař, kterého
najdeme prý v kasárnách městské gardy.“
Vydali se tedy do kasáren stojících u východní městské brány. Jak už to tak
v těchto malých městech bývá, výzbroj místních gardistů byla dost různorodá
– od různě dlouhých mečů přes všelijaká kopí až k náhodně
vypadající sbírce halaparten. Co ale oba rytíře příjemně překvapilo, byla
důslednost, se kterou se místní velitelé věnovali výcviku. Teď zrovna cvičili
gardisté s kopími.
 29-1-3 Střídání zbraní (12 bodů)
29-1-3 Střídání zbraní (12 bodů)
Gardisté městské gardy mají k dispozici přesně tolik kopí, kolik jich v gardě
slouží. Každé kopí je ale jinak dlouhé a jednotliví gardisté jsou také různě
vysocí.
Když si gardisté vybírají, se kterým kopím půjdou bojovat, jsou ochotni si vzít
jenom kopí nanejvýš tak dlouhé, jak jsou oni vysocí (neboli gardista nemůže mít
delší kopí, než je jeho výška).
Při výcviku dbají velitelé na to, aby si co nejvíce gardistů zkusilo bojovat
s co nejvíce různými kopími. Zajímalo by je tedy, kolik existuje různých možností,
jak si gardisté mohou rozdělit kopí tak, aby každý dostal právě jedno a to
nebylo vyšší, než je on sám. Vaším úkolem to je pro zadané délky kopí a výšky
gardistů spočítat.
Příklad: Pro kopí o délkách 7,3,6,1 a pro gardisty vysoké 3,7,4,8
existují celkem 4 možnosti, jak si kopí mohou rozdělit. Gardisté ve výše
uvedeném pořadí dostanou kopí délek (1,6,3,7), (3,6,1,7), (1,7,3,6)
nebo (3,7,1,6).
Řešení
Na dvoře kasáren se rozdělili a začali se co nejnenápadněji vyptávat osamocených
gardistů. Nechtěli moc rozhlašovat svoji příslušnost ke královskému rytířskému
řádu, to by tady daleko v severních krajích mohlo způsobovat problémy. Lepší
bylo zůstat neznámými pocestnými.
Gorfovo písknutí je po chvíli všechny svolalo dohromady. Na jedné straně nádvoří
Gorf objevil malého chlapíka, který odpovídal popisu od kupce.
„Prý jsi zahlédl nějakou velkou potvoru,“ spustil Warin a vtiskl muži do
ruky pár zlaťáků. Muž si Warina nervózně prohlédl a pak je všechny posunkem
vyzval, aby ho následovali za roh. Tam jim začal líčit své setkání s drakem.
Popsal jim, že procházel místem, kudy už předtím šel mnohokrát, když tu se přes
skalní převis nad ním přehnala obrovská potvora – drak. Chvíli se před ním
schovával a pozoroval ho ukrytý ve křoví, čekající na příležitost. A když se
naskytla, tak vyběhl, jak nejrychleji dovedl.
 29-1-4 Zběsilý útěk (10 bodů)
29-1-4 Zběsilý útěk (10 bodů)
Stopaře překvapil v divočině drak, a tak se před ním dal na útěk. Stopař má
představu o tom, jak vypadá okolní terén, takže si naplánoval dostatečně
klikatou trasu na zmatení draka. Okolí se skládá buď z normálně prostupného
terénu, nebo ze strašidelných hustolesů.
Stopařova trasa je tvořena lomenou čárou (neboli na sebe navazujícími úsečkami),
která může procházet i skrz hustolesy, ale v takovém případě v nich stopař
zvládne běžet jen poloviční rychlostí. Hustolesy jsou obdélníkové oblasti, které
budou, stejně jako stopařova trasa, zadány na vstupu.
Navíc máme slíbeno, že každou úsečku na trase protíná nejvýše jeden hustoles
a že hustolesů je zhruba stejně mnoho, jako úseček trasy.
Představu můžete získat třeba z obrázku níže. Vaším úkolem bude spočítat, jak
dlouho bude stopařovi proběhnutí celé trasy trvat.
Při řešení by se vám mohlo hodit nahlédnout do geometrické kuchařky.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku vstupu dostanete tři celá čísla oddělená
mezerou: Nejprve rychlost stopaře v normálním terénu V vyjádřenou v metrech za
sekundu. Dále pak číslo N udávající počet bodů na stopařově trase (mezi těmito
body se stopař pohybuje po úsečce) a nakonec číslo H udávající počet hustolesů
(pozor, jeden hustoles může zasahovat i do více úseček).
Na dalších N řádcích naleznete vždy dvě čísla, každá dvojice udává souřadnice
jednoho z bodů na stopařově trase.
A nakonec na dalších H řádcích najdete vždy 4 čísla
ax,ay,bx,by udávající souřadnice levého dolního a pravého horního rohu
daného hustolesa. Všechny souřadnice jsou zadány v metrech.
Formát výstupu: Na výstup vypište počet sekund, za které stopař překoná
celou trasu, zaokrouhlený na celé sekundy.
Ukázkový vstup:
10 5 2
100 100
350 350
500 500
1100 500
1100 100
100 200 1300 300
400 400 600 600
Stopař celkově uběhne cca 1566 m, z toho cca 483 m hustolesem.
Řešení
Po setkání se stopařem se Gorf vydal zařizovat něco do města, možná se
zkontaktovat s místním cechem zlodějů, což byl také velmi dobrý zdroj informací.
Zbytek družiny se usadil v krčmě a nad džbánkem probíral, co dál.
Byli sem vysláni, aby zjistili více o záhadném nebezpečí ze severu. V království
už nějakou dobu kolovaly historky, že na severu se sbíhají nějaké temné síly,
ale zatím ani král, ani řád neměli žádné důkazy. Jen spoustu mlhavých příběhů od
obchodníků.
Živého draka nikdo neviděl po několik set let. Většinu z nich pobili za dávných dob
drakobijci, a pokud nějací draci přežili, tak se myslelo, že spí nekonečným
spánkem ve svých hlubokých slujích. Tenhle jeden ale rozhodně nevypadal na to,
že by byl vyhuben, ani na to, že by spal nekonečným spánkem. Musela ho probudit
nějaká veliká temná síla.
Warin se zamyslel nad jejich nynější situací a přitom se přes svůj džbánek
zahleděl na druhou stranu stolu. S úsměvem si všiml, jak Lian pokukuje po Rhee.
Rheu znal už spoustu let a vždycky ji vnímal jen jako dobrou přítelkyni. Ale
musel uznat, že je to okouzlující kouzelnice a vůbec se nedivil, že mladý rytíř
z ní může mít hlavu v oblacích. Rhea samotná si toho pravděpodobně byla vědoma,
ale vypadalo to, že jí to vůbec nevadí. Jen kdyby ji Lian pořád neoslovoval
„Mylady“ …
Tok Warinových myšlenek přerušil Gorf, který rozrazil dveře do krčmy, doběhl k jejich
stolu a polohlasem pronesl „Warine, Rheo, Liane, na severní hradby útočí
drak!“
Warin se nerozmýšlel moc dlouho a poslal Gorfa s Rheou přímo na hradby, aby
pomohli obráncům. On společně s Lianem se zatím rozeběhli ke stájím, kde
měli svého nákladního mezka, aby se převlékli do brnění. Byli sice jen čtyři,
ale všichni byli zatraceně dobří bojovníci.
Gorf s Rheou doběhli na hradby právě ve chvíli, kdy se nad nimi přehnal drak,
spálil jeden dům těsně za hradbami a začal se otáčet k dalšímu kolečku. Proti
němu vylétlo sporadicky několik šípů, ale bylo jich málo a navíc se nezkušení
lukostřelci ohrožovali spíše navzájem, než aby trefovali draka. Gorf stáhl ze
zad svůj luk a začal je organizovat.
 29-1-5 Lučištníci (10 bodů)
29-1-5 Lučištníci (10 bodů)
Lučištníci stojící v řadě na hradbě mají vyhlédnuté své cíle. Každý z nich míří
lukem na nějaké místo, ale je neúčinné a nebezpečné, aby všichni stříleli, jak
se jim zachce. Rádi by svou palbu koncentrovali a navíc by měli střílet jen ti,
jejichž dráhy palby se nekříží.
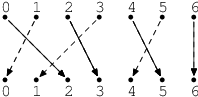
Lučištníky můžeme popsat pomocí bodů, na které míří. Například na obrázku
níže nultý lučištník míří na bod 2, první na bod 0, druhý na bod 3, třetí na bod
1, čtvrtý na bod 5, pátý na bod 4 a šestý na bod 6.
Ze všech lučištníků chceme vybrat co největší skupinu, jejíž dráhy střelby
se nekříží. V uvedeném příkladě jsou to třeba lučištníci 0, 2, 4 a 6
(zvýraznění plnými čarami). Stejně tak by fungovali třeba lučištníci 1, 2,
5 a 6.
Navrhněte algoritmus, který takovou skupinu najde. Pokud existuje
více řešení, stačí oznámit libovolné jedno z nich.
Řešení
Ve chvíli, kdy na hradby doběhli Warin s Lianem v těžké kroužkové zbroji
s bílomodrými štíty, už létaly šípy v mohutných salvách. Drak se raději držel
dál, ale z lesa naproti městské bráně začali vybíhat goblini.
„Kdo k sakru jste?“ vykřikl překvapeně kapitán městské stráže, když se k němu
Warin a Lian rozeběhli. „Rytíři Alvarezova řádu, pokud si chcete zachránit
město, poslouchejte nás!“
Protože oba ozbrojenci vypadali, že jsou mnohem bojeschopnější, než kdokoliv
z jeho mužů, nemluvě o těžké výstroji, kterou nesli, tak kapitán bez větších
námitek souhlasil. Goblini začali dorážet na hradby pomocí žebříků a část
z nich se pokoušela i o proražení brány.

Lian si vzal na starost obranu vršku
hradeb a Warin začal šikovat gardisty dole pod hradbami, aby se připravili na
prolomení brány.
Drak se ale nevzdával. Jakoby ho modrobílé postavičky obou rytířů vyburcovaly
k ještě větší bojechtivosti, začal se střemhlavě vrhat na hradby a svým mocným
dechem je začal spalovat tak, až pukal kámen.
Rhea se ale také činila. Připravovala si štítové kouzlo a nyní ho začala
rozprostírat.
 29-1-6 Štítové kouzlo (10 bodů)
29-1-6 Štítové kouzlo (10 bodů)
Na městské hradby útočí drak a postupně je ničí. Městské hradby si můžeme
představit jako řadu různě vysokých kusů. Drak při každém svém náletu
ubere všem nechráněným kusům hradeb jednu jednotku výšky. Níže, než úplně
do základů, je ale spálit nemůže (výška hradeb nemůže jít do záporných čísel).
Hradby můžeme chránit pomocí štítového kouzla, ale kouzelnice Rhea umí
roztahovat štít vždy jen o jeden kus hradeb mezi každými dvěma drakovy útoky.
Navíc chráněná oblast hradeb musí být souvislá.
Začneme tedy tvořit štít nad libovolným kusem hradeb, který je od této chvíle
chráněn a již se neničí. V každém dalším kroku ho můžeme rozšířit o jedna doleva,
nebo doprava.
Vaším cílem je pro zadané výšky hradeb poradit kouzelnici Rhee, kde má začít
a jak má štít postupně rozšiřovat, aby se v součtu uchránilo co nejvíce hradeb
(tedy aby součet zbylých výšek hradeb byl co největší).
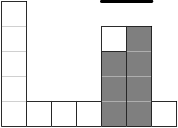
Příklad: Pro hradby vysoké 5,1,1,1,4,4,1 je nejlepší začít se štítem
nad předposledním úsekem hradeb a pak ho rozšiřovat směrem doleva. Tím se nám
povede uchránit celkově 7 dílů hradeb. Kdybychom začali na páté pozici
a rozšiřovali doprava, uchráníme stejně dílů hradeb, kdežto kdybychom začali se
štítem nad nejvyšší hradbou, tak se nám povede uchránit nejvýše 5 dílů hradeb
– vysoké hradby na opačné straně padnou dříve, než nad ně stihneme rozšířit
štít.
Na obrázku jsou znázorněny výšky hradeb a části, které z nich zůstanou, pokud
začneme stavět štít nad předposlední hradbou a roztáhneme ho doleva (další
stavění štítu pak už nic jiného nezachrání).
Řešení
Jeden z posledních drakových útoků vedl na část hradeb, kde Lian odrážel útočící
gobliny. Těsně předtím, než se i zde zhmotnil štít, pronikl drakův útok skrz
a smetl všechny obránce společně s hromadou sutin dolů. Rhea se vyděšeně
ohlédla, Liana však nikde neviděla. Nesměla ale polevit v posilování štítu, na
zachraňování bude čas později!
Městskou bránu mezitím prorazili goblini, ale ani ve snu nebyli připraveni na
modrobílý uragán, který se mezi ně vrhl. Warin rozdával rány na všechny strany,
městští gardisté se sice také snažili, ale úrovně cvičeného alvarezského rytíře
dosáhnout nemohli.
Drak už mezitím utrpěl příliš mnoho zranění od šípů a viděl, že jeho útoky jsou
odráženy štítem, a tak s mocným zařváním svůj pokus vypálit město vzdal a dal se
na ústup. Ve spojení s krvavou lázní u městské brány to na gobliny bylo asi moc.
Většina z nich zpanikařila a začala utíkat nazpět do lesa. Po necelých deseti
minutách už na dohled od brány nezůstal jediný živý goblin.
Když se Warin vrátil s gardisty zpět za městskou bránu, uviděl, jak Rhea a Gorf
usilovně odhazují trámy a kusy zdiva u jedné zřícené části hradeb, Rhea měla
slzy v očích. Hned mu bylo jasné, co se stalo. Odložil zbraně a dal se také do
odhrabování. Vyprostili několik živých a bohužel i několik mrtvých vojáků, když
tu pod sutinami zahlédli modrou a bílou. Po odhození pár trámů Liana konečně
mohli vytáhnout. Nehýbal se.
Pak se náhle ostře nadechl, otevřel oči a rozkašlal. Rhea ho beze slova
sevřela do náruče tak silně, až mu málem vymáčkla dech. Zase byli všichni čtyři
pohromadě a živí a čekala je tady na severu určitě ještě spousta dobrodružství.
Třeba o nich ještě uslyšíme …
Příběh pro vás vyprávěl
Jirka Setnička
 29-1-7 Stromy kolem nás (15 bodů)
29-1-7 Stromy kolem nás (15 bodů)
Pojďte, v letošním seriálu spolu budeme zkoumat stromy.
Ne snad že bychom vás chtěli přeučit na botaniky – půjde nám
o stromy ryze abstraktní, matematické. A ještě více o algoritmy pro práci
s nimi.
Klíč k určování stromů
Definici stromu najdete v kuchařce této série:
je to souvislý graf bez kružnic. To zní učeně, ale kupodivu je to i velmi
praktické: příklady takových stromů potkáváme všude kolem sebe.
Hierarchie – kupříkladu továrna má továrníka, pak ředitele, ten své
náměstky, jejich podřízenými jsou šéfové oddělení, jim podléhají mistři
v dílnách, a tak dále až k řadovým dělníkům. Příslušný strom sestává
z vrcholů (což jsou zaměstnanci) a hran (vztahy „být přímým podřízeným“). (Sám název hierarchie pochází z byzantské řečtiny: hieros znamená
svatý, z toho hiereus je kněz; arché značí moc, vládu. Jak to souvisí:
Původně se hierarchií nazývaly složité vztahy podřízenosti mezi církevními hodnostáři.)
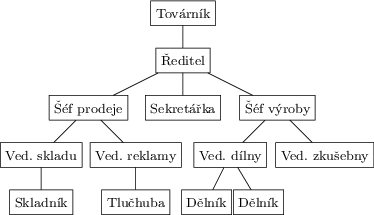
Stromy popisující nějakou hierarchii mají většinou jeden význačný vrchol
– v našem příkladě je to pan továrník, obecně se mu říká kořen stromu.
Jakmile nějaký kořen zvolíme, hned je jasné, kterým směrem je to ve stromu
nahoru (ke kořeni) a kterým dolů. Nenechte se prosím zmást tím,
že na rozdíl od biologů matematici kreslívají stromy kořenem nahoru.
Podle směru také můžeme sousedy každého vrcholu rozdělit na otce
(směrem ke kořeni, v našem příkladě nadřízený) a syny (směrem od kořene,
tedy podřízení). Kořen nemá otce, ostatní vrcholy mají právě jednoho otce.
Listy jsou ty vrcholy, jež nemají syny.
Libovolný vrchol v spolu se všemi svými potomky (to jsou jeho synové, pak synové synů,
atd.) tvoří podstrom, jehož kořenem je v.
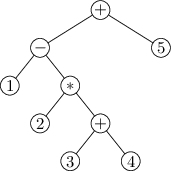
Aritmetický výraz – mějme nějaký výraz s čísly a aritmetickými operacemi,
třeba 1-2*(3+4)+5. Pořadí, v jakém se jednotlivé operace vyhodnocují,
můžeme popsat stromem:
Listy odpovídají zadaným číslům, ostatní (vnitřní) vrcholy jednotlivým
podvýrazům. V každém vnitřním vrcholu bydlí jedna operace, která dostane
mezivýsledky ze svých synů a pošle svůj výsledek otci. V kořeni pak získáme
výsledek celého výrazu. Jelikož běžné operace pracují s právě dvěma čísly,
půjde o strom binární – tedy každý vrchol kromě listů bude mít právě dva
syny.
Městečko lakomců – mapu nějakého městečka si můžeme představit jako obecný graf:
hrany odpovídají ulicím, vrcholy křižovatkám; slepé konce budeme považovat
za speciální případ křižovatek. Pokud ale je pan starosta držgrešle a chce
udržovat co nejméně silnic, brzy z městečka zbude jen kostra, tedy strom
propojující všechny křižovatky. To je příklad stromu, který nemá žádný
přirozený kořen. Můžeme ho tedy zakořenit libovolně, třeba na náměstí s radnicí.
Úkol 1 [1b]
Najděte nějaký další pěkný příklad stromu. Čím méně bude podobný těm
našim, tím lépe.
Reprezentace stromu
Jak stromy reprezentovat v paměti počítače? Zajisté můžeme použít totéž, co
u obecných grafů: vrcholy očíslujeme a pro každý z nich si zapamatujeme
seznam čísel sousedů. Jinými slovy, každý vrchol si pamatuje seznam všech
hran, které z něj vedou.
Zakořeněné stromy obvykle prohledáváme od kořene dolů. Tehdy si stačí v každém
vrcholu pamatovat seznam jeho synů. Někdy se hodí zapamatovat si navíc i otce
vrcholu (případně informaci, že jde o kořen).
Snadno odvodíme, že strom o n vrcholech má přesně n-1 hran: Zakořeníme
ho v libovolném vrcholu a všimneme si, že z každého vrcholu kromě kořene
vede právě jedna hrana do otce. Tak jsme každou hranu započítali právě jednou.
Budeme se proto snažit, aby všechny algoritmy pro práci se stromy
běžely v čase O(n), kde n je počet vrcholů. To postačí na projití všech
vrcholů a hran, ale už ne na cokoliv náročnějšího.
Prohledávání do hloubky
Chceme-li navštívit všechny vrcholy stromu, můžeme to udělat třeba
prohledáváním do hloubky. Začneme v kořeni, a kdykoliv přijdeme
do nějakého vrcholu, rekurzivně se zavoláme na všechny jeho syny.
Přesněji řečeno, nejprve se zavoláme na prvního syna, až se z rekurze
vrátíme (prohledali jsme podstrom pod tímto synem), zavoláme se na druhého
syna, a tak dále.
Abychom lépe viděli, jak prohledávání do hloubky probíhá, doplníme
do něj výpis levé závorky při vstupu do vrcholu a pravé při jeho opuštění.

DFS(v):
- Vypíšeme
(.
- Pro všechny syny s vrcholu v:
- Zavoláme DFS(s)
- Vypíšeme
).
Spustíme-li algoritmus DFS (tak se mu říká podle anglického názvu depth-first
search) na náš příklad stromu výrazu, vypíše ((()(()(()())))()).
Všimněte si, že jsme strom jakoby „obešli po obvodu“ – kdykoliv jdeme po hraně
dolů, píšeme levou závorku, kdykoliv nahoru, pravou. Navíc přidáme jeden úplně vnější
pár závorek.
Celý průchod stromem trvá O(n): v každém vrcholu strávíme čas O(1
+ počet synů). Pokud to posčítáme přes všechny vrcholy, jedničky se
sečtou na n a počty synů na n-1.
Během procházení stromu můžeme také zpracovávat hodnoty uložené ve vrcholech,
třeba je zase vypisovat. Můžeme je vypsat hned při navštívení vrcholu
(tomu se říká
preorder neboli
prefixový výpis), nebo až při opuštění
(
postorder,
postfixový výpis), případně mezi návštěvami synů (
inorder,
infixový). Porovnejme, jak to dopadne:
| prefixový | (+(-(1)(*(2)(+(3)(4))))(5)) |
| postfixový | (((1)((2)((3)(4)+)*)-)(5)+) |
| infixový | (((1)-((2)*((3)+(4))))+(5)) |
Infixový zápis tedy (až na přebytečné závorky) odpovídá tomu, jak obvykle výrazy
zapisujeme. Aby se hodnoty v listech neztratily, samozřejmě je vypisujeme přímo,
i když mezi žádnými syny neleží.
Postfixový zápis má zase tu hezkou vlastnost, že je jednoznačný i bez závorek.
I z očesaného 1 2 3 4 + * - 5 + můžeme rekonstruovat celý strom.
Podobně pro prefixový zápis.
Úkol 2 [2b]
Vymyslete algoritmus, který vytvoří strom z jeho postfixového výpisu
bez závorek. Vyzkoušejte si to třeba na výrazech.
Úkol 3 [1b]
Ukažte dva různé binární stromy se stejným infixovým zápisem bez závorek.
Jak vypadá jejich prefixový a postfixový zápis?
Výpočty pomocí DFS
Spoustu vlastností stromů můžeme počítat rekurzivně: stačí je umět spočítat
pro listy a pak říci, jak z výsledků pro podstromy stanovit výsledek pro celý
strom. Takový výpočet jde jednoduše zabudovat do DFS.
Začněme triviálním příkladem.
Počet listů – stačí vracet z listů jedničku a ve vnitřních
vrcholech hodnoty sčítat:
PočetListů(v):
- Je-li v list, vrátíme 1.
- ℓ←0
- Pro všechny syny s vrcholu v:
- ℓ←ℓ+ PočetListů(s)
- Vrátíme ℓ.
Jelikož jsme každý krok prohledávání jenom konstanta-krát zpomalili,
algoritmus má opět lineární složitost.
Hloubka stromu – tak se říká délce nejdelší cesty z kořene do listu
(délka cesty se měří v hranách). Opět ji spočítáme úpravou DFS: nahlédneme,
že hloubka stromu je o jedna více než maximum z hloubek podstromů (nejdelší
cesta z kořene do listu musí vést z kořene do některého podstromu a pak
pokračovat nejdelší cestou uvnitř podstromu). Hloubka listu je 0. Lineární
algoritmus následuje:
Hloubka(v):
- Je-li v list, vrátíme 0.
- h ←0
- Pro všechny syny s vrcholu v:
- h ←max(h, Hloubka(s))
- Vrátíme h+1.
Úkol 4 [4b]
Vymyslete, jak spočítat průměr stromu. Tak se říká délce nejdelší cesty.
Pozor, není to totéž jako hloubka stromu, protože nejdelší cesta nemusí vést
„shora dolů“ (v příkladu s továrnou jedna taková vede mezi skladníkem a
některým z dělníků).
Vyhodnocení výrazu – výraz reprezentovaný stromem můžeme
snadno vyhodnotit: kdykoliv se vracíme z vrcholu, spočítáme
výsledek příslušného podvýrazu. Pro list vrátíme číslo v něm uložené, ve vnitřních
vrcholech vezmeme hodnoty ze synů a aplikujeme na ně operaci uloženou ve vrcholu.
Strážníci – ve „stromovém“ městečku bují zločin (lidé kreslí křídou na chodníky
karikatury radních!). Starosta chce na vybrané křižovatky rozestavět strážníky tak,
aby každá ulice byla z alespoň jedné strany hlídaná. Jak už ale víme, je to skrblík.
Pro každou křižovatku proto zjistil, kolik musí zaplatit strážníkovi, aby tam byl
ochoten stát, a hledá celkově nejlevnější rozestavění strážníků.
Formálně řečeno, hledáme podmnožinu vrcholů stromu, která z každé hrany obsahuje
alespoň jeden vrchol a navíc je součet cen vrcholů v množině nejmenší možný.
Nabízí se opět zapřáhnout DFS a vracet z podstromů, jak nejlaciněji je jde ohlídat.
Jenže pak nedovedeme z výsledků pro podstromy zkombinovat výsledek pro celý strom.
Pomůže, když si pro každý podstrom místo jednoho čísla spočítáme rovnou dvě.
Budeme jim říkat h a o.
To první („hlídaná cena“) bude udávat, kolik nejméně stačí zaplatit na ohlídání
hran podstromu za podmínky, že v kořeni podstromu bude stát strážník.
Naopak o („opuštěná cena“) hlásá minimální cenu za podmínky, že kořen je opuštěný.
V listu je triviálně h rovno ceně listu a o=0 (podstrom nemá žádné hrany,
takže není potřeba nic hlídat).
Nyní se podívejme na obecný podstrom s kořenem
v ceny
cv se syny
s1,… ,sk, pro které už známe
h1,… ,hk a
o1,… ,ok. Počítejme
h: pokud je kořen hlídaný,
jeho strážník ohlídá všechny hrany vedoucí do synů. V synech si proto mužeme vybrat, zda tam
umístíme strážníka či nikoliv, takže pro
i-tý podstrom postačí
min(hi,oi)
peněz. Celkově tedy
h = cv + ∑ min(hi,oi).
A nyní
o: Jestliže do kořene strážníka nedáme, musí být strážníci ve všech synech
(jinak by některá z hran do synů nebyla hlídaná). Proto
o = ∑ hi.
Všechna h a o tedy hravě spočítáme pomocí DFS v čase O(n).
Odpověď na starostovu otázku pak získáme jako minimum z h a o kořene.
Strážníci(v):
- cv ←cena vrcholu v
- Je-li v list, vrátíme (cv,0).
- h ←cv, o ←0
- Pro všechny syny s vrcholu v:
- (hs,os) ←Strážníci(s)
- h ←h + min(hs,os)
- o ←o + hs
- Vrátíme (h,o).
Úkol 5 [4b]
Strážníci si pořídili drony a dokáží hlídat i „za jeden roh“. Přesněji řečeno,
ulice je hlídaná, pokud stojí strážník na alespoň jedné z krajních křižovatek,
nebo na křižovatce, která s krajní sousedí. Pomozte najít nejlevnější rozestavění
strážníků pro ohlídání všech ulic.
Vandalská indukce a centrum stromu
Ukážeme si ještě jeden způsob, jak zkoumat stromy. Tentokrát je budeme
procházet od listů směrem „dovnitř“. Začneme dvěma jednoduchými pozorováními,
přičemž netriviální budeme říkat stromům s alespoň dvěma vrcholy.
Pozorování 1: Každý netriviální strom má nějaký list.
Důkaz: Strom si zakořeníme v libovolném vrcholu a podíváme se na nejhlubší
vrchol (nejvzdálenější od kořene). Ten nemá žádné syny a vede z něj jediná hrana
do otce. Proto je to list.
Pozorování 2: Odstraníme-li z netriviálního stromu list, vznikne opět strom.
Důkaz: Je třeba ověřit, že graf zůstal souvislý a bez kružnic. Odstraněním
vrcholu jsme sotva mohli vytvořit novou kružnici. Pokud byly nějaké dva neodebrané
vrcholy spojené cestou, budou spojené i nadále, protože odebraný list nemůže ležet
uvnitř cesty.
Z toho plyne následující, poněkud vandalská, technika indukce: ve stromu najdeme
list, odtrhneme ho, čímž získáme další strom. Postup opakujeme, dokud nám nezůstane
triviální strom. Jestliže zaznamenanou posloupnost odebírání listů obrátíme, dostali
jsme postup, jak z jednoho vrcholu postupným přilepováním listů vytvořit původní
strom.
Pokud má ovšem celý algoritmus seběhnout v lineárním čase, nemůžeme listy hledat
pokaždé znovu. Budeme si udržovat frontu objevených, ale dosud neutržených listů.
Na začátku spočítáme stupně všech vrcholů a listy přidáme do fronty. V každém dalším
kroku odebereme jeden list z fronty a odstraníme ho ze stromu.
Jeho sousedovi snížíme stupeň o jedničku, a pokud se tento soused stal listem,
přidáme ho do fronty. Každý vrchol se dostane do fronty právě jednou a jeho
obsluhou strávíme konstantní čas. Celé otrhávání tedy beží v čase O(n), jak
jsme chtěli.
Můžete si zkusit vymyslet, jak tuto „vandalskou indukci“ použít na libovolný
z příkladů, které jsme řešili pomocí DFS. Není divu – když se DFS vrací z rekurze,
také postupuje od listů ke kořeni. My zde ukážeme, jak najít „střed“ stromu,
což se přímo pomocí DFS dělá obtížně.
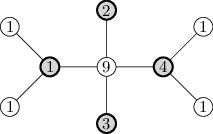
Definice: Pro libovolný vrchol v zavedeme jeho excentricitu (výstřednost)
jako maximum ze vzdáleností z v do ostatních vrcholů. (Pokud bychom tedy strom
ve v zakořenili, bude nám to říkat, jak hluboko je nejhlubší list.) Centrum
stromu říkáme množině všech vrcholů s nejmenší možnou excentricitou.
Příklad vidíte na následujícím obrázku. Čísla udávají excentricity, zvýrazněný
vrchol je centrem stromu.
Dokážeme, že centrum každého stromu je tvořeno buďto jedním vrcholem, anebo dvěma
vrcholy spojenými hranou. Navíc ho lze najít v lineárním čase.
Nejprve si všimneme, že centrum stromu neobsahuje žádný list, neboť soused
listu má o jedničku nižší excentricitu. Aby tato úvaha fungovala, nesmí
být soused listu také list, takže strom musí mít aspoň 3 vrcholy.
Nyní se nám bude hodit, že odstraněním všech listů se sníží excentricity
všech ostatních vrcholů právě o 1. Každá nejdelší cesta z vnitřního vrcholu totiž
končila v nějakém listu, tím pádem jsme ji zkrátili o jednu hranu.
Zkombinujeme-li tyto dvě vlastnosti, zjistíme, že „očesáním“ všech listů
dostaneme menší strom, který má stejné centrum. Opakováním tohoto postupu
graf „oloupeme“ až na jedno- nebo dvouvrcholový strom. U těch snadno nahlédneme,
že jejich centrum obsahuje všechny vrcholy.
K nalézání listů nám opět poslouží fronta. Jen musíme umět rozlišit, kde
končí listy z jedné „slupky“ a začínají ty z další. K tomu stačí do fronty
přidávat zarážku za konec slupky, případně střídat dvě fronty. V obou případech
to stihneme v lineárním čase. Může to vypadat třeba následovně:
- Založíme dvě prázdné fronty F a G.
- Všem vrcholům spočítáme stupně.
- Listy přidáme do F.
- Dokud strom obsahuje alespoň 3 vrcholy:
- Dokud je F neprázdná:
- v ←další vrchol z F
- Odebereme v.
- Pro všechny sousedy s vrcholu v:
- Snížíme stupeň s o 1.
- Pokud stupeň klesl na 1, přidáme s do G.
- Prohodíme F a G.
- Zbývající vrcholy prohlásíme za centrum.
Pro strom z předchozího obrázku proběhne výpočet takto:
Úkol 6 [3b]
Navrhněte a naprogramujte algoritmus, který v daném stromu spočítá excentricity
všech vrcholů.
Martin „Medvěd“ Mareš
Řešení

 29-1-1 Připálené placky (8 bodů)
29-1-1 Připálené placky (8 bodů)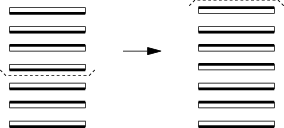

 29-1-4 Zběsilý útěk (10 bodů)
29-1-4 Zběsilý útěk (10 bodů)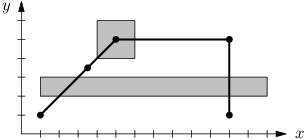


 29-1-7 Stromy kolem nás (15 bodů)
29-1-7 Stromy kolem nás (15 bodů)