Tuto velmi zajímavou sérii úloh vám zcela jistě přinesli organizátoři KSP, ne pan Nápověda. Na to se můžete stoprocentně spolehnout.
Čtvrtá série třicátého ročníku KSP
Celý leták v PDF.
- Termín série: 14. května 2018
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží každý, kdo odevzdá alespoň tři úložky alespoň týden před termínem a získá za ně kladný počet bodů.
Zadání úloh
- 30-4-1: Černobílé hádání
- 30-4-2: Kočka na stromě
- 30-4-3: Hippocoin
- 30-4-4: Malování 2.0
- 30-4-5: Frňákovník
- 30-4-6: Takřka nudná úloha
- 30-4-7: Překřikující se procesory
 30-4-1 Černobílé hádání (9 bodů)
30-4-1 Černobílé hádání (9 bodů)
Náš kamarád má pole o n černých a bílých políčkách. Je ale poněkud stydlivý,
takže nám pole nechce ukázat. Po krátkém přemlouvání nám prozradil aspoň
hodnotu n a také to, že v poli je přesně m souvislých úseků stejné barvy
(například v poli ###..## jsou tři), přičemž m je řádově menší než n.
Kamarád je navíc ochoten odpovídat na dotazy „Je v úseku [a, b] aspoň
jedno políčko bílé/černé?“ Na co nejméně dotazů zjistěte, jak vypadá celé pole.
 30-4-2 Kočka na stromě (10 bodů)
30-4-2 Kočka na stromě (10 bodů)
 Kočka vylezla na strom a neumí slézt. Hasiči ji jedou zachránit. Potřebují
dorazit co nejrychleji, takže se vydají po nejkratší cestě. Mohlo by se ale
stát, že tato cesta nebude průjezdná. Chtějí tedy vyslat ještě jedno záložní
auto po jiné nejkratší cestě, která nebude s trasou prvního auta mít společné
nic kromě začátku a konce.
Kočka vylezla na strom a neumí slézt. Hasiči ji jedou zachránit. Potřebují
dorazit co nejrychleji, takže se vydají po nejkratší cestě. Mohlo by se ale
stát, že tato cesta nebude průjezdná. Chtějí tedy vyslat ještě jedno záložní
auto po jiné nejkratší cestě, která nebude s trasou prvního auta mít společné
nic kromě začátku a konce.
Poněkud matematičtěji řečeno, máte zadán ohodnocený neorientovaný graf a dva vrcholy označené jako start a cíl. Vaším úkolem je najít mezi nimi dvě vrcholově disjunktní nejkratší cesty, pokud existují. Tím myslíme dvě cesty, které jsou obě nejkratší (tedy stejně dlouhé) a nemají žádný společný vrchol kromě startu a cíle.
Na následujícím obrázku vidíte příklad grafu s vyznačenými dvěma vrcholově disjunktními nejkratšími cestami (délky 7):
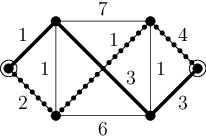
Ale například pro následující graf řešení neexistuje – obsahuje celkem čtyři nejkratší cesty, jenže všechny procházejí jedním společným vrcholem:
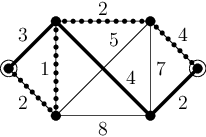
 30-4-3 Hippocoin (10 bodů)
30-4-3 Hippocoin (10 bodů)
Na soustředění KSP vznikla nová kryptoměna hippocoin. Chceme využít situace a vydělat obchodováním s hippocoiny co nejvíce peněz. Hippocoin lze kupovat a prodávat za peníze. Každý den je vyhlášena nákupní a prodejní cena a my pak máme možnost koupit, nebo prodat libovolný počet hippocoinů. Kupní cena je přitom vždy vyšší, nebo rovná prodejní a všechny ceny jsou kladné. Na začátku máme dané množství peněz a v průběhu obchodování nikdy nesmíme mít záporné množství hippocoinů ani peněz.

Hippocoiny i koruny jsou libovolně dělitelné – lze obchodovat s libovolně malým zlomkem hippocoinu. Máme k dispozici předpověď, jaká bude nákupní a prodejní cena hippocoinu v každém z následujících k dní. Chceme zjistit, jak obchodovat (tedy kolik hippocoinů který den nakoupit či prodat), abychom na konci k-tého dne měli co nejvíce korun, pokud se bude cena vyvíjet přesně podle naší předpovědi.
 Lehčí varianta (za 7 bodů): Vyřešte úlohu pro případ, kdy nákupní cena je vždy stejná jako
prodejní.
Lehčí varianta (za 7 bodů): Vyřešte úlohu pro případ, kdy nákupní cena je vždy stejná jako
prodejní.
 30-4-4 Malování 2.0 (12 bodů)
30-4-4 Malování 2.0 (12 bodů)
Právě vyšla nová verze programu Malování! Umí sice jenom černobílé obrázky o n ×m pixelech, ale zato nabízí skvělý nový nástroj: magický štětec. Ten všem pixelům ve čtverci k×k okolo místa, kam jsme klikli, prohodí barvu na opačnou. Zatím jsme nepřišli na to, kde se velikost čtverce dá nastavit, takže k považujeme za konstantu.
Přesněji: Pokud klikneme na políčko se souřadnicemi (a,b), prohodí se barva všem pixelům (x,y) takovým že, a≤ x<a+k a b≤ y<b+k. Čtverec nesmí přečnívat přes okraj obrázku, tedy musí platit a+k < n, b+k < m.
Zajímá nás, které obrázky se magickým štětcem dají nakreslit. Dostaneme zadaný černobílý obrázek velikosti n×m a velikost štětce k. Máme zjistit, zda lze tento obrázek vytvořit používáním magického štětce na zpočátku bílou plochu.
 30-4-5 Frňákovník (10 bodů)
30-4-5 Frňákovník (10 bodů)
Na tržišti se objevil tajuplný stánek, v němž bělovlasá stařena s bradavicí na nose prodává džus z frňákovníku. Jak jistě víte, stačí ho vypít jedinou sklenku a nos se vám prodlouží do nevídaných rozměrů, k velkému pobavení širého okolí. Jaký by to byl skvělý dárek na narozeninovou párty vašeho nejlepšího nepřítele!
Stařena je ovšem poněkud vybíravá v tom, komu a jak džus prodá. Každý si musí přinést své vlastní nádoby, které mu naplní až po okraj. Navíc je ochotna prodat pouze takové celkové množství džusu, které je násobkem 7 dl.
Pořídili jste si N různých nádob s celočíselnými kapacitami k1, …, kN dl a chcete z nich vybrat takové, aby součet jejich objemů byl násobkem 7 dl a přitom byl co největší. Vymyslete algoritmus, který tyto nádoby najde.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete celé číslo N udávající počet nádob. Na každém z dalších N řádků dostanete celé číslo udávající objem jedné nádoby v decilitrech.
Formát výstupu: Na první řádek vypište dvě celá čísla oddělená mezerou:
největší množství džusu, které lze zakoupit, a počet nádob,
které při tom budou naplněny (k). Na dalších k řádků vypište pořadová
čísla použitých nádob. Nádoby číslujeme od nuly v pořadí, v jakém se objevily
na vstupu. Pokud existuje více správných řešení, vypište libovolné. Pokud
neexistuje žádné řešení, vypište jen první řádek obsahující 0 0.
Počet nádob a jejich objemy jsou menší než 231, ale na součty už můžete
potřebovat 64-bitová čísla (long long v Céčku).
5 2 3 2 2 17
21 3 0 3 4
 30-4-6 Takřka nudná úloha (14 bodů)
30-4-6 Takřka nudná úloha (14 bodů)
Na vstupu máme dva textové řetězce. Chceme najít jejich nejdelší společnou
podposloupnost. Co se tím myslí? Podposloupnost vznikne z posloupnosti vyškrtáním
některých prvků: například abc, acdf nebo prázdný řetězec jsou
podposloupnostmi řetězce abcdef. Nevyškrtnuté prvky přitom musí zůstat v původním
pořadí. Naším cílem je najít nejdelší řetězec, který je podposloupností obou
zadaných řetězců.
Nuda, řeknete si – tohle je přeci dobře známá úloha, na kterou existuje algoritmus s časovou složitostí O(n2) a paměťovou také O(n2) pro dva řetězce délky n. Najdete ho například v naší kuchařce o dynamickém programování.
Kdepak, žádná nuda to nebude. Zadané řetězce jsou totiž tak dlouhé, že si nemůžeme dovolit víc než lineárně mnoho paměti. Vymyslete proto co nejrychlejší algoritmus na nalezení nejdelší společné podposloupnosti, kterému stačí O(n) paměti. Prozradíme ještě, že by se k tomu mohla hodit i kuchařka na metodu Rozděl a panuj.
 30-4-7 Překřikující se procesory (15 bodů)
30-4-7 Překřikující se procesory (15 bodů)
Vývoj počítačů se žene vpřed. Toužíme po čím dál rychlejších procesorech, ale stále víc při tom narážíme na technické limity, či spíš rovnou na fyzikální zákony. Řešením může být pořídit si místo čtyřikrát rychlejšího procesoru čtyři stejně rychlé. Ostatně, většina dnešních počítačů tak vypadá – mluví se sice obvykle o více jádrech, ale minimálně z pohledu programátora to jsou samostatné procesory.
Programovat několik procesorů, které se všechny najednou snaží pracovat se společnými daty, je velké dobrodružství. Pojďme si ho v posledním dílu našeho seriálu vyzkoušet. Tu a tam si sice realitu trochu zjednodušíme, ale všechny zásadní radosti a strasti paralelního světa při tom okusíme.
Pořídíme si počítač s několika ARMovými procesory, které mají společnou paměť.
Jelikož program je uložen v paměti, znamená to, že také mají společný program.
Každý procesor má ale svou sadu registrů včetně sp a pc, takže
může vykonávat svou část programu a mít k tomu svůj zásobník. Takovému uspořádání
se říká symetrický multi-processing neboli SMP.
Poněkud naivní pokus
Začneme triviálním problémem: chceme si pořídit počítadlo a zvyšovat ho, kdykoliv v programu kteréhokoliv z procesorů nastane určitá událost. Pojďme si tedy pořídit nějaké místo v paměti, uložit do něj 4-bajtové počítadlo a zvyšovat ho následující posloupností instrukcí:
@ v r0 očekáváme adresu počítadla
LDR r1, [r0]
ADD r1, #1
STR r1, [r0]
Hotovo. Co by se mohlo stát špatně? Inu, ledacos…
Představme si třeba následující scénář. V paměti je hodnota 100.
Procesor A si řekne, že počítadlo zvýší, tak do r1 přečte 100
a přičte 1. Než stihne zapsat r1 zpět do paměti, procesor B
se také pokusí zvýšit počítadlo. (To se může stát, protože rychlost
provádění programu závisí na spoustě okolností, takže někdy je jeden
procesor rychlejší než druhý.) Procesor B také přečte 100 a vzápětí
zapíše 101. Teď se dostane ke slovu opět procesor A, ale vůbec neví,
co se mezitím stalo, takže zapíše tu 101, kterou má stále v r1.
Místo dvou zvýšení počítadla tedy nastalo jen jedno.
Mohlo by to být i horší: co kdyby se hodnoty do paměti zapisovaly po
částech, například po jednotlivých bajtech? Při přechodu počítadla
z 0x0000ffff na 0x00010000 by mohla být chvíli v paměti
hodnota 0x0001ffff a jiný procesor by ji mohl stihnout přečíst.
To se naštěstí na ARMu nestane: máme zaručeno, že instrukce LDR
a STR pracující se správně zarovnanými daty jsou takzvaně atomické.
To znamená, že vždy provedou celou operaci najednou a ostatní procesory
ji vidí buďto ještě neprovedenou, nebo už zcela provedenou.
Exkluzivní přístupy do paměti
Náš předchozí pokus tedy nefungoval hlavně proto, že mezi přečtením počítadla a jeho zápisem zpět mohl jiný procesor počítadlo změnit. ARM nám naštěstí umožňuje si této nečekané změny počítadla všimnout.
Existuje instrukce LDREX (LoaD Register EXclusive), která se chová stejně
jako LDR, ale navíc si procesor zapamatuje, že má adresu, z níž se četlo, hlídat.
Sleduje pak ostatní procesory, jestli některý z nich také neudělal LDREX
ze stejné adresy.
Když pak místo instrukce STR použijeme STREX na hlídanou adresu,
zápis do paměti se provede jen tehdy, pokud k adrese mezitím nikdo jiný nepřistoupil.
V opačném případě se dozvíme, že se zápis nepovedl. Instrukce STREX
má proto tři parametry: chybový registr (do něj se uloží 0 v případě úspěchu
a 1 při neúspěchu), zdrojový registr a cílovou adresu v paměti.
V našem příkladu s počítadlem tedy můžeme zjistit, že se počítadlo během našeho zvyšovaní změnilo, a v takovém případě přečtenou hodnotu zahodit a pokus o zvýšení zopakovat od začátku. Vypadat to bude takto:
@ v r0 očekáváme adresu počítadla
pokus:
LDREX r1, [r0]
ADD r1, #1
STREX r2, r1, [r0]
CMP r2, #0
BNE pokus
Pokud bychom chtěli přistupovat k jednotlivým bajtům nebo 16-bitovým
číslům, existuje také (LD|ST)REX(B|H). Také můžeme použít 64-bitovou
variantu (LD|ST)REXD, která čte/ukládá dva registry po sobě (počáteční
adresa musí být dělitelná 8).
Dodejme ještě, že procesor umí v jeden okamžik hlídat jenom jednu adresu.
Pokud provedeme LDREX v okamžiku, kdy už nějaká adresa byla hlídaná,
předchozí hlídání se zruší. Pokud se pokusíme o STREX na adresu,
která zrovna není hlídaná, skončí neúspěšně. Pakliže nějaký jiný procesor
přistupuje k hlídané adrese jiným způsobem než pomocí těchto instrukcí,
není zaručeno, že si jich hlídací mechanismus všimne.
Zámky
Někdy se hodí trochu obecnější přístup: říci o nějakých datech (v našem případě počítadle, ale může to být třeba celá složitá datová struktura), že s ní smí v jeden okamžik zacházet nejvýše jeden procesor. K tomu se hodí pořídit si zámek neboli mutex (z anglického mutual exclusion – vzájemné vyloučení).
Zámek je objekt, který má dva stavy: odemčeno a zamčeno. Na počátku je v odemčeném stavu. Chce-li nějaký procesor pracovat s chráněnými daty, pokusí se zámek uzamknout. Pakliže byl v tomto okamžiku zámek odemčený, stane se zamčeným a program hned pokračuje. Až bude operace s daty hotova, program zámek odemkne a tím data zpřístupní ostatním procesorům. Pokud byl při pokusu o zamykání zámek uzamčen jiným procesorem, program čeká, dokud jiný procesor zámek neodemkne.
Nejjednodušší forma zámku je takzvaný spinlock. V paměti bude uložen jako 4-bajtová proměnná. V odemčeném stavu v ní bude 0, v zamčeném 1.
Zamčení spinlocku můžeme provést atomicky pomocí
LDREX a STREX:
zamkni: @ r0 = adresa zámku
LDREX r1, [r0]
CMP r1, #0
BNE zamkni @ už bylo zamčeno
MOV r1, #1
STREX r2, r1, [r0]
CMP r2, #0
BNE zamkni @ někdo nás předběhl
Odemčení je triviální: stačí do proměnné zapsat nulu
obyčejným STR – náš procesor je jediný, který
v daný okamžik může spinlock odemykat, takže se s nikým
nepředháníme.
odemkni: @ r0 = adresa zámku
MOV r1, #0
STR r1, [r0]
Náš příklad s počítadlem by se tedy dal naprogramovat stylem „zamkni spinlock, zvyš počítadlo, odemkni spinlock“. Program sice vyjde delší, ale snáz se o něm přemýšlí. Proto se spousta problémů se sdílením dat mezi procesory řeší právě pomocí zámků. Je ale potřeba dát si pozor na několik věcí:
- Předně nechceme zámek udržovat zamčený příliš dlouho – obvykle jenom na dobu nějaké elementární operace s daty. Jinak by totiž jednotlivé procesory většinu času trávily jenom čekáním na zámky.
- Podobně nechceme všechna data chránit jedním společným zámkem. Raději si pro každou datovou strukturu pořídíme samostatný zámek. Na druhou stranu nechceme zámek přidávat ke každé trivialitě, protože pak by nám polovinu paměti zabraly zámky.
- Nikdo nám nezaručuje, za jak dlouho se zamčení zámku povede.
Uvažujme třeba tuto situaci: máme dva procesory, které se současně
pokoušejí o zamčení téhož spinlocku. První z nich provede
LDREX, pak druhý takéLDREX. OběSTREX, ať už v libovolném pořadí, pak nutně selžou. Oba procesory tedy svůj pokus zopakují od začátku, načež opět selžou, a tak dále. Tento problém nás naštěstí v praxi neohrožuje, protože provádění programu závisí na spoustě vnějších okolností, takže se oba procesory po několika pokusech rozejdou natolik, že už si nebudou překážet. Exaktně dokázat to nicméně nedovedeme, aspoň s naším primitivním modelem procesoru.
Úkol 1 [3b]
Často se nám hodí dovolit několika procesorům číst společná data, ale nechceme do nich ani paralelně zapisovat, ani současně zapisovat a číst. Naprogramujte read-write spinlock. Ten má 3 stavy: odemčeno, zamčeno pro čtení a zamčeno pro zápis. V každém okamžiku musí být buďto odemčený, nebo zamčený pro čtení na libovolně mnoha procesorech, případně zamčený pro zápis na právě jednom procesoru.
Bariéry
Přístup „zamknu, modifikuji, odemknu“ se nám sice osvědčil, ale tak, jak jsme ho popsali, by nefungoval spolehlivě. Byl totiž založený na představě procesoru, který vykonává instrukce pěkně po pořadě. Skutečný procesor ale trochu „švindluje“ – sice tak, aby běžící program nemohl nic poznat, leč z jiných procesorů to už poznat může být.
Podívejme se třeba na tuto posloupnost instrukcí:
MOV r1, #0 @ 1
STR r1, [r0] @ 2
STR r1, [r0, #4] @ 3
LDR r1, [r0, #8] @ 4
STR r1, [r0] @ 5
Instrukce 2 a 3 ukládají na dvě různá místa v paměti. Kdyby procesor zápisy do paměti provedl v opačném pořadí, program by nemohl nic poznat, protože mezitím žádná data z paměti nečte. Procesor toho může využít, pokud mu z nějakého důvodu přijde prohozená varianta lepší než původní.
Podobně může procesor zápis do paměti o pár instrukcí posunout: program by například nepoznal, kdyby se zápis z instrukce 2 provedl až mezi instrukcemi 4 a 5. Za instrukci 5 ho ale posunout nemůžeme, protože ta zapisuje na totéž místo v paměti.
Procesor by si nicméně mohl všimnout, že data zapsaná instrukcí 2 jsou přepsaná instrukcí 5 a mezi tím je nikdo nepřečte. Proto by mohl zápis z instrukce 2 úplně zrušit.
Konečně v instrukci 4 čteme data, do kterých žádná z předchozích instrukcí nemůže zapisovat, takže procesor může čtení provést už dříve. To je také běžná optimalizace: paměť je pomalá, takže může pomoci zadat jí požadavek na čtení dat v předstihu, aby v okamžiku, kdy data budeme potřebovat, už byla připravena.
Obecně platí, že procesory mohou přístupy do paměti libovolně přeházet, dokud si jsou jisté, že tím neovlivní chod programu. O chodu programu na jiných procesorech ovšem nic nevědí, takže jejich „ekvivalentní úpravy“ programu nakonec mohou uškodit.
Uvažujme následující program:
- Zamkneme spinlock S
- počítadlo ←počítadlo+1
- Odemkneme spinlock S
Uvnitř operací se spinlocky se na proměnnou počítadlo nesahá, takže procesor může přesunout její čtení i zápis mimo oblast chráněnou spinlockem a tím celý náš pečlivě budovaný mechanismus ochrany vyřadit.
To je samozřejmě nanejvýš nepraktické, proto existují takzvané bariéry
– to jsou instrukce, přes které není dovoleno přehazovat některé typy přístupů
do paměti. My si vystačíme s univerzální bariérou, což je instrukce DMB
(Data Memory Barrier). Přes ni není dovoleno přehodit žádné čtení ani zápis.
V našem příkladu bychom tedy chtěli jednu bariéru umístit mezi kroky 1 a 2 a druhou mezi 2 a 3. To je tak častý obrat, že obvykle bariéry zabudováváme přímo do implementace zámků: na konec zamykání a na začátek odemykání.
Bariéry se mohou hodit i v jiných případech. Představte si, že budujete spojový seznam nějakých položek. Při vkládání nejprve vyplníte položku (obyčejnými neatomickými instrukcemi, protože je to mnohem jednodušší) a pak ji atomicky vložíte do seznamu. Tehdy ovšem hrozí, že ostatní procesory narazí při čtení seznamu na ukazatel na novou položku, ale když se do této položky podívají, ještě v něm neuvidí správný obsah. Proto je potřeba mezi vyplnění položky a její zařazení do seznamu přidat bariéru.
Paralelní seznamy
Ukažme si několik příkladů paralelní práce se seznamy. Začněme jednoduše: pořídíme si více jednosměrných spojových seznamů. Seznam bude mít hlavičku, ve které si bude pamatovat ukazatel na první prvek a zámek, který chrání všechna data seznamu. Kdykoliv chceme se seznamem provést nějakou operaci, nejprve zamkneme zámek, pak provedeme operaci a nakonec zámek odemkneme. To zaručí, že každá operace bude korektní (procesory si nebudou navzájem přepisovat ukazatele v seznamech), a přitom půjde současně pracovat s různými seznamy.
Problém nastane, pokud se pokusíme atomicky přehodit prvek ze seznamu A do seznamu B (atomicitou myslíme, že pro správně zamykajícího vnějšího pozorovatele bude v každém okamžiku tento prvek v právě jednom seznamu). Mohli bychom to udělat tak, že nejprve zamkneme zámek seznamu A, pak zámek seznamu B, načež prvek přepojíme a nakonec oba zámky odemkneme.
To je triviální … a špatně. Rozbije se to, pokud se jeden procesor bude snažit přehodit prvek z A do B a současně s tím jiný procesor nějaký jiný prvek z B do A. První procesor si stihne zamknout A a než stihne zamknout B, zamkne si ho druhý procesor. Nyní první procesor čeká na B a druhý na A, ale ani jeden z nich se nedočká odemčení. Tomuto stavu se říká deadlock (česky poněkud méně elegantně uváznutí).
Podobně by deadlock mohl nastat, pokud by se první procesor pokoušel přehazovat prvek z A do B, druhý z B do C a třetí z C do A. Možnosti, jak se mohou věci pokazit, jsou zkrátka nepřeberné :)
Úkol 2 [4b]
Naprogramujte atomické přehazování prvků mezi seznamy tak, aby nemohlo dojít k deadlockům. Správnost se pokuste dokázat.
Podívejme se ještě na dva úkoly na atomickou práci se seznamy. Nemusíte v něm rozepisovat všechny detaily do instrukcí, stačí dostatečně podrobný pseudokód. Operace se zámky, přístupy do paměti a bariéry z něj nicméně musí být jasné.
Úkol 3 [4b]
Naprogramujte frontu: jednosměrný spojový seznam, který si pamatuje ukazatel jak na začátek, tak na konec. Má umět operace „přidej na konec“ a „odeber ze začátku“. Přitom chceme, aby práce se začátkem a s koncem mohla probíhat současně (není-li zrovna fronta příliš krátká).
Úkol 4 [4b]
Naprogramujte seznam počítadel: jednosměrný spojový seznam dvojic (klíč, počet), kde všechny klíče jsou různé. Má umět dvě operace: „zvyš počet pro daný klíč a pokud ještě neexistovala dvojice s tímto klíčem, založ ji“ a „sniž počet pro daný klíč a pokud se snížil na nulu, dvojici odstraň“. Obě operace vrací novou hodnotu počtu. Snažte se, aby operace mohly probíhat co nejvíce paralelně.
Virtuální realita
V celém seriálu jsme se věnovali tomu, jak se programuje v assembleru, pokud nám do toho nikdo další nemluví. Skutečnost ale bývá komplikovanější: na počítači obvykle běží více programů, někdy i patřících více uživatelům, a místo aby se bavily přímo s hardwarem, bdí nad nimi operační systém a hlídá, aby se programy o hardware nepřetahovaly a navzájem si neškodily.
Fungování operačních systémů by vydalo na samostatný seriál (třeba někdy…), ale pokusme se na závěr alespoň pár věcí naznačit.
Procesory především mají dva různé režimy: uživatelský a systémový. Po zapnutí se procesor ocitne v systémovém režimu a začne vykonávat instrukce operačního systému. V tomto módu procesor není chod programu nijak omezen. Když chce časem spustit nějaký obyčejný program, nahraje ho na správné místo do paměti, vyhradí mu místo na zásobník, nastaví počáteční hodnoty registrů a přepne se do uživatelského režimu. V tom jsou některé věci zakázány a je přístupná pouze část paměti (například obvykle nelze přímo ovládat různá vstupně-výstupní zařízení počítače).
Musí tu ale být možnost, jak se dostat zpátky do systémového režimu – program
může skončit, nebo může třeba chtít po operačním systému, aby mu přečetl nějaká
data z disku. Nelze ovšem uživatelskému programu dovolit, aby jen tak přepnul
režim a začal vykonávat své instrukce v systémovém režimu. Proto existuje mechanismus
systémových volání. Na ARMu existuje speciální instrukce SVC (SuperVisor
Call), která přepne do systémového režimu a začne vykonávat kód od adresy, kterou
si předtím operační systém nastavil (v paměti, do které uživatelský kód neměl právo
zapisovat).
Často také chceme oddělit nejen systémovou paměť od uživatelské, ale také oddělit data jednotlivých uživatelských programů. K tomu se používá virtualizace paměti. Uživatelské programy pak neadresují fyzickou paměť, nýbrž se procesor nastaví tak, aby všechny adresy překládal podle speciální tabulky. Program tedy přistupuje k nějakým virtuálním adresám a tabulka říká, jak se tyto adresy přeloží na fyzické (případně může být řečeno, že nějakou část paměti je třeba dovoleno pouze číst). Tabulku přitom systém nastaví každému uživatelskému programu jinak, takže programy žijí ve svém virtuálním světě a o ostatních programech nevědí (případně s nimi mohou komunikovat skrz operační systém).
Uživatelských programů, které chceme spouštět, je mnohdy víc, než má náš počítač fyzických procesorů. I tady nahradíme skutečnost vhodnou iluzí. Systém si udržuje libovolně mnoho procesů, které by chtěly běžet. Každý proces má přidělenou nějakou paměť (a vytvořenou překladovou tabulku ze svých virtuálních adres na fyzické), v ní má své instrukce, svá data a svůj zásobník, a navíc si u něj systém pamatuje aktuální stav registrů.
Součástí systému je pak plánovač neboli scheduler, který rozhoduje, kdy má který proces běžet a na kterém procesoru se spustí. Pokud je procesů víc než procesorů, každý proces nechá běžet jenom chvíli, než se buďto sám rozhodne zastavit, nebo uplyne vhodná doba. Pak místo něj plánovač spustí další proces, přičemž se snaží přidělovat procesům procesory nějak spravedlivě.
Pokud tedy chceme programovat paralelně, obvykle systému neříkáme, co má spustit na kterém procesoru, ale prostě si pořídíme více procesů se společnou pamětí (těm se obvykle říká vlákna čili threads) a necháme plánovač, ať je rozhazuje mezi procesory, jak se mu hodí.
Při tomto přístupu je samozřejmě dost nešikovná naše implementace zámků pomocí spinlocků – pokud zamkneme spinlock, načež nás plánovač přeruší a spustí jiný proces, který by také chtěl tento spinlock, onen jiný proces pořád čeká ve smyčce na něco, čeho se před dalším přeplánováním nemůže dočkat. Místo toho by bylo lepší, kdyby se při neúspěšném pokusu o zamčení zámku vzdal procesoru a nechal se probudit až v okamžiku, kdy je zámek odemčen. Tomu se říká pasivní čekání (na rozdíl od aktivního u spinlocků). Operační systém vám obvykle dodá implementaci zámků, která čeká pasivně.
Ale to už je opravdu jiný příběh. Pojďme odemknout všechny zámky, přeplánovat a spustit proces prázdniny…
PS: Vlákna v simulátoru
Abyste si své výtvory mohli vyzkoušet, přidali jsme do simulátoru podporu více vláken. Ta je aktivována, pokud máte v programu návěští ve tvaruthreadčíslo,
např. thread5. Pro každé takovéto návěští simulátor vytvoří jedno vlákno,
které na začátku skočí na dané návěští a dál vykonává kód od tohoto místa.
Protože jde o vlákna spravovaná operačním systémem, nemůžeme zaručit, že kód poběží
současně a na různých procesorech. Pokud vlákna poběží krátce, může se například
stát, že se nejdřív provede celé první vlákno a potom celé druhé.
O ukončení vlákna se musíte postarat sami, např. skokem na konec.
Program skončí po doběhnutí všech vláken nebo uplynutí časového limitu 15 s.
Vícevláknový mód nevypisuje na konci automaticky obsah registrů (protože
každé vlákno má svoje registry a nebylo by to moc přehledné). Pokud potřebujete
nějaké ladící výpisy, můžete si třeba zavolat printf.