Pátá série třicátého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu si vyslouží každý, kdo získá alespoň 15 bodů z obou seriálových úloh dohromady. Seriál můžete odevzdávat až do 30. června.
Zadání úloh
Úvodem
Ačkoliv by to tak někdy mohlo vypadat, my orgové na vás účastníky nezapomínáme.
Až si budete venku užívat teplých dnů, které připomínají spíše léto než jaro,
nezapomeňte si s sebou přibalit i toto zadání, ve kterém naleznete poslední
sadu úloh tohoto ročníku. Získáte dostatečný počet bodů a diplom úspěšného
řešitele? Pojedete na Podzimní soustředění? Ať už to vyjde nebo ne, doufáme, že
jste si z řešení tohoto ročníku odnesli nové znalosti a zkušenosti a že
nepovažujete čas strávený nad úlohami za promarněný.
Díky řešení KSP se také můžete vyhnout přijímacím zkouškám na MFF UK! Stačí,
když získáte alespoň polovinu bodů z ročníku (tedy 150 bodů) a my vám vystavíme
osvědčení úspěšného řešitele, díky kterému vás (nejdříve příští školní rok)
přijmou na MFF bez zkoušek.
Kromě úloh této série jsme také vydali
třetí a
čtvrtý
díl seriálu o assembleru. Můžete ho řešit až do 30. června.
Ve třetí sérii jsme orgy opustili, protože to vypadalo, že pana Nápovědu už
konečně dostali…
„Podle časových záznamů k tomu výbuchu došlo okamžitě potom, co jsme se
teleportovali. Nápověda neměl sebemenší šanci to přežít. Navíc se ten
japonský gang rozpadl.“
* * *
„Pomóóóóc! Nápověda je tady!“
Ale vraťme se na začátek.
* * *
Orgové si po poslední akci protentokrát řekli, že stíhání zločinců už bylo
dost, a že by místo toho mohli začít stíhat deadliny Jarního soustředění.
Oproti všem očekáváním týden s novými řešiteli proběhl poměrně organizovaně.
Unavení, ale spokojení účastníci se na konci týdne vydali do svých domovů a
organizátorům jen zbývalo rozvézt věci, které během týdne používali. Obzvlášť
velké množství se uchovává v budově na Malé Straně, v jednom ze zdejších
trezorů.
Trezorů? Ale opravdu! Kdysi budova Matfyzu sloužila jako sídlo Československé
národní banky a v několika velkých trezorech pod budovou se
uschovávaly státní rezervy zlata. Po přestěhování banky se ale
trezory proměnily ve skladiště všemožného harampádí. Tlusté kovové dveře teď
zůstávají pořád otevřené, koneckonců se od nich ztratily klíče.
Aspoň že část jednoho z trezorů patří KSPčku. Jirka s Filipem před chvílí
přijeli autem do dvora malostranské budovy a naložili všechny věci ze
soustředění na pojízdný vozík. „Proč mám dojem, že na každý sous toho vozíme
víc a víc?“ podíval se Jirka kriticky na obsah vozíku. „Projedeme tím
vůbec?“
 30-5-1 Úklid po soustředku (11 bodů)
30-5-1 Úklid po soustředku (11 bodů)
Jirka s Filipem se chystají krabice s potřebami na soustředění naložit na vozík
a ten odvézt do jednoho z podzemních trezorů. Chodby k trezoru
jsou však úzké a nemuseli by tam projet. Naštěstí mají k dispozici vozíky
různých velikostí. Protože věcí je hodně, rádi by si vzali největší vozík,
se kterým ještě projedou. Vozíky jsou čtvercové a dostupné ve všech možných
velikostech: od 1×1 po velké jako celá budova (neptejte se, kde je
skladují).
Prostor, v němž se orgové mohou pohybovat, si zakreslíme jako obdélníkové
bludiště o M řádcích a N sloupcích, přičemž každé pole buď je, nebo není
průchozí. Známe počáteční pozici vozíku (přesněji jeho levého horního rohu) a
máme zakreslenou pozici trezoru (jedno políčko), do níž ho chceme dovézt.
V každém kroku mohou organizátoři posunout celý vozík o jedno políčko doleva,
doprava, nahoru nebo dolů. Vždy však všechna pole vozíku musí být na průchozích
polích.
Rádi bychom určili největší možnou velikost vozíku, se kterou se dá dojet
do trezoru. Také bychom chtěli najít nejkratší cestu, po které s takovým vozíkem
do cíle jet. Za dosažení cíle považujeme, když se libovolná část vozíku ocitne
na cílovém políčku. Délkou cesty rozumíme celkový počet kroků (posunů vozíku).
Uvažume například následující bludiště:
Do cíle se dostaneme s vozíkem velkým nejvýše 3×3 a jedna z možných
nejkratších cest je naznačena čarou (sleduje levý horní roh vozíku). Čárkovaně
je naznačen obrys vozíku na začátku a konci trasy. Světle šedá jsou všechna
políčka, na kterých se někdy vyskytla libovolná část vozíku. Nejkratší cesta
má 13 kroků.
Řešení
Stěhování vozíku proběhlo úspěšně a naše dvojice se ocitla v trezoru, jehož
stěny byly obložené hromadou skříněk. Jirka si oddychl, utřel pot z čela a
chtěl začít vykládat vozík do té, co patří KSPčku. Všimne si ale, že Filip
zaujatě zírá na strop trezoru. „Nechceš mi pomoct? Takhle tu budeme do
rána…“ řekne naštvaně utahaný Jirka a pak si teprve všimne, co tam Filipa
zaujalo.
Celý strop je pokreslený otazníky. Spousta otazníků, velké, malé, v různých
barvách. „To je ale dementní vtip,“ řekne Jirka. „Koho tohle napadlo?“
Pak si oba uvědomí, že slyší nějaké kroky z chodby. „Je tu někdo?“ zavolá
Filip. Kdyby se někdo ve sklepě nacházel, jistě by to zjistili už při příchodu.
Ale u dveří do sklepení se tradičně potkali jenom s lidskou kostrou, která má
za úkol vystrašit nezvané hosty.
„Je tu někdo?“ zavolá Jirka hlasitěji. A u dveří do trezoru se skutečně
někdo objeví. Je to ta kostra ze vchodu! Skrze její lebku ale prosvítá něčí
zašedlý obličej. A bedny uložené na vozíku se začnou otevírat a věci z nich
začnou vystřelovat směrem na Jirku a Filipa!
Když Filipovi naplno dojde, že vidí oživlou kostru, ztuhnou mu nohy. Když
připustí, že kostra má obličej, ztuhnou mu ruce. A v okamžiku, kdy se na něj
sám od sebe začne sypat obsah vozíku, mu dojde, že teď může akorát buď omdlít,
nebo začít ječet a utíkat.
Začne ječet a utíkat a následovat Jirku, který udělal to samé. Běží směrem
k východu ze sklepení, jenže ten je zavřený a nejde otevřít. „Nemůžeme ty
dveře odpálit?“ „Na vozíku byly výbušniny! Brali jsme je na
soustředko!“
 30-5-2 Útěk z trezorů (11 bodů)
30-5-2 Útěk z trezorů (11 bodů)
I v této úloze se orgové ocitli v bludišti malostranských sklepů, ale jejich
situace je o mnoho vážnější. Zjistili, že ze své pozice se nedostanou
k východu. Mají ale možnost v nějaké chodbě odpálit výbušninu, čímž by se jim
možná otevřela cesta k úniku.
Opět máme obdélníkové bludiště o R řádcích a S sloupcích, každé pole
bludiště může, ale nemusí být průchozí. Je zadané startovní a cílové pole,
mezi nimiž ovšem neexistuje přímá cesta po průchozích polích. Máme k dispozici
výbušninu se silou popsanou čísly A a B. Pokud ji necháme explodovat na
poli, které je přístupné ze startu, zničíme obdélník o (2A + 1) řádcích a
(2B + 1) sloupcích, jehož střed se nachází v poli. Všechna pole v obdélníku
se stanou průchozími.
Rozhodněte, které místo v bludišti odpálíte, abyste mohli projít mezi startem a
cílem, a zda takové místo vůbec existuje.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku jsou čtyři čísla R, S, A, B
oddělená mezerami. Následuje R řádků o S sloupcích, na každém popis
jednoho políčka bludiště: mezera značí volné políčko, # zeď,
^ startovní políčko a $ cílové.
Formát výstupu: Dvě mezerou oddělená čísla: souřadnice políčka,
na kterém chceme nechat explodovat výbušninu. Nejprve uvedeme číslo řádku,
pak číslo sloupce, obojí počítané od 0.
Ukázkový vstup:
4 5 1 1
#^ ##
##
#$# #
###
Po odpálení bomby na pozici [1, 2] bude bludiště vypadat takto:
#^ #
#
#$ #
###
Správné jsou například i odpovědi 0 1 nebo 2 3. Naproti tomu 3
1 není správná odpověď, protože toto políčko není dosažitelné ze startu.
Řešení
„Stejně by to nestačilo, ta stěna je hrozně tlustá. A já už zpátky do toho
trezoru nejdu… Musíme to zkusit po druhých schodech.“ S bušícím srdcem se
oba vydali na druhou stranu sklepení. Aby toho nebylo málo, kvůli úsporným
opatřením tady nesvítila světla.
 30-5-3 Energetické úspory (11 bodů)
30-5-3 Energetické úspory (11 bodů)
Vedení Matfyzu zjistilo, že fakultní budova na Malé Straně spotřebovává velké
množství elektrické energie, proto se rozhodli co nejvíc osekat její spotřebu.
Mimo jiné se zaměřili na sklepení budovy. To je z velké části nepoužité, stejně
tu však všude svítí světla. Správci budovy vytipovali tři důležité body, mezi
nimiž je nutné osvětlení zachovat (například vstup do sklepení nebo důležitý
trezor).
Máte zadaný nákres sklepení budovy, skládající se ze křižovatek, které jsou
propojeny chodbami. Pro každou chodbu znáte její délku v metrech. Tři
křižovatky jsou označené jako důležité. Řekněte nám, které chodby nechat
osvětlené, aby se mezi jakýmikoliv dvěma důležitými křižovatkami dalo dostat
přes osvětlené chodby a aby součet délek osvětlených chodeb byl co nejnižší.
O struktuře chodeb nemůžete nic předpokládat – klidně se může stát, že mezi
dvěma křižovatkami vede mnoho různých cest. Rovněž se chodby mohou křížit
mimoúrovňově.
Jinými slovy: máte zadaný neorientovaný ohodnocený graf a v něm tři význačné
vrcholy. Chcete najít nejmenší podmnožinu hran (měřeno součtem jejich délek)
takovou, že mezi každými dvěma význačnými vrcholy vede cesta po hranách
z této množiny.
Řešení
Jirkovi s Filipem se podařilo dostat do počítačové laboratoře. Zastavili se
uprostřed místnosti. Vypadala klidně, ale orgové si rychle všimli, že se nad
jejich hlavami chvěje lustr. O vteřinu později se ozvalo zasvištění a nějaká
neznámá síla začala srážet ze stolů počítačové displeje. „Pryč!“ Vyběhli
k východu a za svými zády uslyšeli třeskot padajícího lustru. „To snad není
pravda!“ Bylo už pozdě v noci a východ z budovy byl zamčený. Vyběhli po
schodech, Filip se na chvíli rychle ohlédl a u vchodu do laboratoře zahlédl tu
samou tvář, kterou spatřili dole ve sklepě. Tentokrát však nebyla na kostlivci,
místo toho plula ve vzduchu a doširoka jí plály oči. Tvář byla zešedivělá a
hrozivá, ale přesto Filip poznal, že patří Nápovědovi.
Běželi po schodech a snažili se vyhýbat těžkým věcem, které na ně duch Nápovědy
(protože co jiného by to mohlo být?) házel. Zezadu slyšeli chechot a nadávky.
Aniž by vůbec přemýšleli nad zastavením, doběhli až na půdu. Zavřeli se do
jedné z místností a natahali ke dveřím stůl a židle, aby je nešlo otevřít.
* * *
Chvíli jim trvalo, než popadli dech.
„Takže první věc, duchové existují,“ pronesl Filip. „Druhá věc, je to
duch chlápka, který má důvod nás nesnášet, protože jsme ho zabili. A ta třetí
věc, nemáme tušení, jak si s ním poradit.“
Jirka se rozhlédl. „Tady jsem ještě nebyl a nevím, kdo tu pracuje, ale ten
člověk asi moc informačním technologiím nefandí.“ V místnosti nebyl počítač,
místo toho se v policích nacházela hromada kartoték. Jirku zaujala ta s nápisem
Lidé a kontakty. „Papírová sociální síť? Jestli hledáš kontakt na
vymítače duchů, možná by byl rychlejší internet,“ ušklíbl se Filip.
Zvenku někdo praštil do dveří a málem odsunul barikádu z nábytku.
„Takže ty myslíš, že na internetu jen tak najdeš kontakt na typického
vymítače duchů? Nový a přehledný web s rozesmátými obličeji, referencemi a
tlačítkem Kontaktujte nás? Nebo dokonce s live chatem?“ zakroutil hlavou Jirka.
„To bych spíš věřil téhle kartotéce. Kromě telefonních čísel tu je i
napsáno, čím se ten člověk zabývá.“
 30-5-4 Kartotéka (10 bodů)
30-5-4 Kartotéka (10 bodů)
Jeden z velmi konzervativních profesorů na Matfyzu si uchovává informace
o různých osobách v papírové kartotéce. Každá karta odpovídá jedné osobě. Kromě
kontaktních údajů si také profesor do jedné z kolonek na kartě zapisuje, přes
jakého prostředníka se s osobou zná. Tento prostředník má v kartotéce také kartu.
Pokud zná profesor někoho osobně, tak je v kolonce napsané přímo profesorovo
jméno. Samotný profesor má v kartotéce speciální kartu se svými údaji (protože
je často sám zapomene). Platí, že pokud vezmeme kartu odpovídající jakékoliv osobě
a následujeme odkazy na prostředníky, dojdeme do profesorovy karty.
Jeden z doktorandů profesora přemluvil, aby si kartotéku uložil do počítače.
Datová struktura, reprezentující kartu, obsahuje mimo jiné i ukazatel na kartu
prostředníka. Ukazatel je vždy platný s výjimkou profesorovy struktury, kde je
nulový. I tady se vždy dokážeme dostat do profesorovy struktury, prostě budeme
následovat ukazatele.
Máte adresy na dvě karty v operační paměti. Uvažujte řetězec z každé
z nich až do profesorovy karty a najděte místo, kde tyto řetězce srůstají. Má to
komplikaci – protože počítač je starý téměř stejně jako pan profesor, můžete si
během výpočtu používat jen konstantně mnoho pomocné paměti. Do karet samotných
nesmíte nic zapisovat.
Na obrázku představuje P profesorovu kartu. Řetězce karet A a B srůstají
v C, ale A a D až v P.
Řešení
I když Jirka listoval kartotékou rychle, Filip byl přece jen o něco rychlejší.
„Haló? Je tam Chryzantéma Bělohlavová? Já vím, že je pozdě večer, ale právě
jsme zjistili, že duchové existují! Cože?“ Filip vzal ze stolu tužku a papír a
začal na něj rychle něco čmárat. „Nestihnete se sem včas dostat? A jste si
jistá, že nám tohle pomůže?“, nadskočil, když se ozvalo další praštění do
dveří, „Tak vám zkusíme věřit,“ zavěsil telefon.
Filip v rychlosti Jirkovi vysvětlil, co mu Chryzantéma poradila. Musí z papíru
sestrojit těleso o určitých specifických rozměrech. Pro výpočet rozměrů
Ghostbusteru, jak orgové těleso nazvali, je ale třeba znát největší společné
dělitele některých čísel.
 30-5-5 Výroba likvidátoru (11 bodů)
30-5-5 Výroba likvidátoru (11 bodů)
 Ghostbuster je výsledek nejnovější vědecké práce předních ezoteriků. Jde
o papírové zařízení, které dokáže porazit duchy a jakékoliv jiné nepozemské
kreatury. Při výrobě je ale třeba dbát na to, aby rozměry byly co nejpřesnější.
K jejich výpočtu je třeba znát největší společné dělitele řady čísel.
Ghostbuster je výsledek nejnovější vědecké práce předních ezoteriků. Jde
o papírové zařízení, které dokáže porazit duchy a jakékoliv jiné nepozemské
kreatury. Při výrobě je ale třeba dbát na to, aby rozměry byly co nejpřesnější.
K jejich výpočtu je třeba znát největší společné dělitele řady čísel.
Jistě víte, jak je definovaný největší společný dělitel dvou přirozených čísel
A a B – jde o takové největší možné číslo, které dělí A i B. Tuto
definici jde ale snadno rozšířit o větší množství čísel než dva, stačí říct, že
hledané největší možné číslo musí dělit všechny z nich.
Máme seznam N různých kladných celých čísel. Chceme jedno z těchto čísel
vyškrtnout, aby platilo, že největší společný dělitel zbylých čísel je
největší možný.
Řešení
Další náraz na dveře! Jirka k nim zpátky přitlačil stůl a s poděšením sledoval
Filipa, jak zápasí s papírem, nůžkami a lepidlem. „Už ho dlouho neudržím!“
„V klidu, už jsem hotový,“ ukázal Filip hotový Ghostbuster.
„A tohle nás jako zachrání?“ vytřeštil oči Jirka, když si prohlédl papírový
výtvor. „Vždyť to vypadá jako rozbitej čtyřrozměrnej dopravní kužel!“
Filipa začala přemáhat nervozita. „Tak si zkus sám!“ hodil po něm
Ghostbusterem. „Ani náhodou!“ mrštil ho Jirka zpátky. „Ty ses bavil
s Chryzantémou.“
Obří náraz přerušil jejich konflikt. Dveře se otevřely a dovnitř vletěla
pobledlá Nápovědova hlava a z očí jí šlehaly blesky. Filip, který málem vyletěl
z okna, z posledních sil natáhl ruku, jako kdyby chtěl tasit meč. Jenže místo
meče držel papírovou skládanku pro děti…
* * *
Chryzantéma Bělohlavová se dostala na místo činu a když vyběhla na půdu budovy,
spadl jí kámen ze srdce. Ti dva matfyzáci byli sice notně pošramocení a
vyděšení, ale nebylo to nic, co by její alternativní medicína nezvládla.
Ohořelý Ghostbuster se válel uprostřed místnosti – duch Nápovědy byl zřejmě
navždy pryč. Přesto ho svým šestým ezo-smyslem cítila a vnímala zbytky jeho
myšlení. Musela uznat, že neměl úplně jednoduché dětství. I během té záplavy
vzteku ho neopustily některé nepříjemné vzpomínky ze školy.
 30-5-6 Nápověda na lyžích (13 bodů)
30-5-6 Nápověda na lyžích (13 bodů)
Jako žák základní školy jel Nápověda na lyžařský kurz. Byl v té době docela
obtloustlý a lyžování mu vůbec nešlo. V závěrečném testu na konci kurzu měl
docela jednoduchý úkol – projet mezi několika lyžařskými brankami. Ani to se
mu ale nepovedlo a spolužáci si z něj dlouho dělali legraci.
Na vstupu dostanete popis lyžařského svahu. Jde o (v matematickém smyslu)
rovinu, na níž se nachází tyčky dvou druhů, východní a západní. Tyčky ale
nejsou nijak spárované, netvoří žádné branky nebo něco podobného. Svah je
skloněný podél osy Y, při jízdě po svahu se hodnota souřadnice snižuje.
Tlustý lyžař má za úkol jet na lyžích zeshora dolů tak, aby projel napravo od
všech západních tyček a nalevo od všech východních tyček. Musí pak jet naprosto
rovně (jeho trajektorie je přímka), kvůli své tloušťce ale zabírá kruhovou
plochu o průměru D.
Při jakém maximálním D ještě může lyžař projet? Neboli, jaká je maximální
šířka pásu, kterým od sebe dokážeme oddělit východní a západní tyčky?
Řešení
Všimla si, že Jirka s Filipem se už pomalu dostali z šoku. „Všechno
v pořádku?“ zeptala se. „Až zase natrefíte na nějakého jiného ducha, tak už
budete v klidu.“
„S tím máme trochu problém, nějak se pořád nemůžeme smířit s tím, že duchové
skutečně existují. Až to povíme řešitelům, tak nás za to sežerou.“
„Tak od toho odveďte pozornost.“
„Ale jak? Tohle je poslední série. Nápověda je mrtvý, příběh už pokračování
mít nebude, tak jak máme odvést pozornost řešitelů?“
„Říkali jste, že na soustředění berete výbušniny?“
Kuba Maroušek
 30-5-1 Úklid po soustředku (11 bodů)
30-5-1 Úklid po soustředku (11 bodů)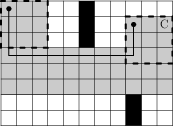
 30-5-2 Útěk z trezorů (11 bodů)
30-5-2 Útěk z trezorů (11 bodů)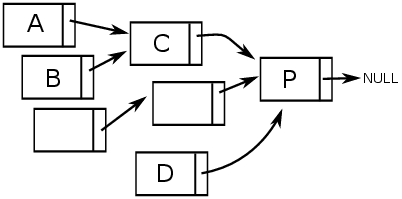
 Ghostbuster je výsledek nejnovější vědecké práce předních ezoteriků. Jde
o papírové zařízení, které dokáže porazit duchy a jakékoliv jiné nepozemské
kreatury. Při výrobě je ale třeba dbát na to, aby rozměry byly co nejpřesnější.
K jejich výpočtu je třeba znát největší společné dělitele řady čísel.
Ghostbuster je výsledek nejnovější vědecké práce předních ezoteriků. Jde
o papírové zařízení, které dokáže porazit duchy a jakékoliv jiné nepozemské
kreatury. Při výrobě je ale třeba dbát na to, aby rozměry byly co nejpřesnější.
K jejich výpočtu je třeba znát největší společné dělitele řady čísel.