Pátá série třicátého druhého ročníku KSP
Celý leták v PDF.
Na křídlech léta za vámi plachtí vzorová řešení poslední série letošního KSP. Přejeme příjemné čtení, ať už někde u vody, nebo v přízračném svitu monitoru za tiché letní noci :)
Těšíme se na vás v příštím ročníku, jehož zadání se objeví začátkem září. A také na podzimním soustředění, na něž začneme brzy rozesílat pozvánky.
Vaši organizátoři
Řešení úloh
- 32-5-1: Poničený zdrojový kód
- 32-5-2: Propojovací kabely
- 32-5-3: Bomberman uklízí efektivně
- 32-5-4: Distribuované počítání
- 32-5-5: Druhá kostra
- 32-5-6: Geocaching s odhadem
 32-5-1 Poničený zdrojový kód (Zadání)
32-5-1 Poničený zdrojový kód (Zadání)
Na úvod si řekneme, že pokud je počet závorek na vstupu lichý, tak řešení
neexistuje, jinak můžeme každou posloupnost převést na {}{}{}…
Dále již budeme předpokládat, že počet závorek je sudý.
Zkusme si nejdříve vyřešit jednodušší problém. Máme posloupnost závorek a chceme říci, jestli jsou správně uzávorkované. Uvažme následující algoritmus:
Zřídíme si zásobník a budeme číst jednotlivé znaky a po každém načtení provedeme:
- Pokud je to znak
{, tak přidáme znak do zásobníku. - Jinak se podíváme do zásobníku a pokud je na vrchu zásobníku
{, tak znak vyndáme ze zásobníku (našli jsme pár), jinak přidáme do zásobníku}.
Pokud na konci algoritmu máme zásobník prázdný, tak víme, že na vstupu jsme měli validní uzávorkovanou posloupnost.
Proč to funguje? Zkusme si rozmyslet situaci, když se k sobě dostane pár závorek
{}. Tyto závorky nás v tuto chvíli přestaly zajímat, protože nemůžeme danou
otevírající závorku již napárovat na jinou zavírající závorku, protože jinak by
výraz nebyl již správně uzávorkován. Stejné tvrzení platí i pro zavírající závorku.
Tento pár je již k ničemu a můžeme ho na něho zapomenout/smazat.
U správně uzávorkované posloupnosti (pokud není prázdná) existuje vždy minimálně jeden
pár závorek {}, které jsou přímo vedle sebe. Když tyto páry odstraníme, tak se
minimálně jeden další vytvoří, dokud posloupnost není prázdná.
Teď si promysleme, jak bude zásobník vypadat, když výraz není zcela správně uzávorkován. Zásobník bude rozdělen na dvě části. První část bude tvořena jen zavírajícími závorkami a druhá část bude tvořena jen otevírajícími závorkami. Obě části můžou být různě velké či prázdné. Je důležité si uvědomit, že na zásobníku se nemůže stát, že bude vedle sebe otevírající a uzavírající závorka, protože všechny tyto páry jsme již vymazali výše zmíněným algoritmem.
Nyní mějme bez újmy na obecnosti na vrchu zásobníku dvě otevírající závorky. Pro další kombinace závorek, konkrétně pro dvě zavírající závorky nebo zavírající a otevírající závorku, bude postup fungovat obdobně. Teď si představme, jak dané dvě otevírající závorky vypadají v původní posloupnosti. Mezi těmito závorkami je nějaká posloupnost, která je správně uzávorkována (posloupnost může být i prázdná). Pokud otočíme druhou otevírající na zavírající, tak vytvoříme korektní pár, který zabaluje posloupnost mezi danými závorkami a dohromady tvoří správně uzávorkovanou posloupnost.
Na výstupu jsme chtěli, jaké konkrétní závorky otočíme. Tento problém vyřešíme tak, že do zásobníku nebudeme vkládat přímo znaky závorek, ale budeme vkládat jen indexy daných znaků v původní posloupnosti.
Nyní stačí si promyslet, proč otočíme minimální počet závorek. Výše zmíněným algoritmem odstraníme všechny validní páry. Po skončení algoritmu zůstanou v zásobníku ty závorky, které nemůžou tvořit páry, a musíme tyto páry vytvořit. U dvou stejných závorek stačí otočit jedna závorka. Pokud jsou závorky různé, tak musíme otočit obě. Tento případ vznikne, pokud části mají lichou délku.
Časová složitost je O(n), kde n je počet závorek. Stačí si jen uvědomit, že každou závorku do zásobníku vložíme a z něj odstraníme maximálně jednou.
Paměťová složitost je O(n).
 32-5-2 Propojovací kabely (Zadání)
32-5-2 Propojovací kabely (Zadání)
Pro dodržení standardního grafového názvosloví budeme místo určování typu konektoru dané vrcholy obarvovat.
Každá barva bude mít nějakou cenu a bude odpovídat právě jednomu typu konektoru. Barvy budeme indexovat posloupností přirozených čísel a budeme předpokládat, že jsou setříděné dle hodnoty.
Jednoduchý algoritmus
Graf si zakořeníme v libovolném vrcholu. Nejprve můžeme uvážit následující dynamické programování: Pro každý vrchol a jeho obarvení spočítáme hodnotu optimálního řešení jeho podstromu za předpokladu, že daný vrchol má tuto barvu.Tyto hodnoty lze počítat dynamikou od listů. Každou z nich spočítáme následovně: K ceně daného obarvení přičteme pro každého potomka minimum z optimálního řešení jeho podstromu pro všechny barvu kromě aktuálně počítané. Takto spočítáme všechny hodnoty.
Zrychlování
Toto řešení budeme dále vylepšovat. Vždy při výpočtu totiž nepoužíváme přímo hodnoty dynamického programování, ale minimum z hodnot kromě nějaké barvy. Tedy si přímo můžeme pamatovat tato minima.Ovšem minima jsou poněkud jednotvárná. Pro každý vrchol jsou totiž všechna až na jedno (nebo dokonce všechna) stejná. Minimum z původního dynamického programování se projeví ve všech kromě jednoho. Tedy pro každý vrchol si budeme pamatovat pouze minimální hodnotu a druhou nejmenší z původního dynamického programování a barvu, na které je ona minimální hodnota (dále říkejme optimální barva daného vrcholu). Pro rekonstrukci řešení si budeme uchovávat i barvu druhého nejlepšího řešení.
Ukážeme, že i tyto hodnoty umíme elegantně počítat od listů. Uvážíme všechny optimální barvy přímých potomků. Pro každou z nich vypočítáme optimální hodnotu podstromu za předpokladu, že aktuální vrchol má tuto barvu. Dále pak vypočítáme i tuto hodnotu pro dvě barvy s nejmenšími cenami, které nejsou optimální pro ani jednoho přímého potomka. Ostatní barvy není třeba uvažovat. Ve výsledku se totiž nemůžou projevit. Mají evidentně horší výsledek než ony dvě v potomcích neobjevující se barvy (stejná hodnota ze všech potomků – maximum a větší cena daného vrcholu). Ze stejného důvodu můžeme dokonce ignorovat i všechny barvy s vyšší cenou než druhá z dvojice potomky neurčených barev, protože jejich hodnota je ještě o to větší.
Přímé potomky si tedy uložíme do přihrádek podle optimálních barev (přihrádky ve formě spojových seznamů pro každou barvu jeden budeme mít připravené už na začátku algoritmu a pak je vždy využijeme a zase vyprázdníme). Poté tyto přihrádky budeme procházet od nejlevnějších do té doby dokud nalezneme druhou bez umístěného potomka (nebo nedojdeme na jejich konec).
Pro každou procházenou přihrádku spočítáme optimální hodnotu podstromu za předpokladu, že aktuální vrchol bude mít tuto barvu. Ovšem procházet vždy všechny přímé potomky by bylo moc pomalé. Proto si nejprve předpočítáme součet minim všech přímých potomků. Každou přihrádku pak projdeme následovně: Pouze u vrcholů v dané přihrádce bude využita druhá nejmenší hodnota, tedy stačí projít všechny tyto vrcholy a přičíst rozdíl jejich hodnot. Finálně ještě přičteme hodnotu aktuálně počítané barvy.
Takto spočítáme každou procházenou přihrádku. Po konci průchodu přihrádek po sobě uklidíme: projdeme znovu všechny přímé potomky a smažeme přihrádky jejich optimálních barev. Postupně si budeme pamatovat nejnižší a druhou nejnižší hodnotu (a jejich indexy). Tyto hodnoty jsou pak výsledkem pro aktuálně počítaný vrchol.
Dá se nahlédnout, že ani stejné hodnoty při výpočtu (ať už cen jednotlivých vrcholů nebo optimálních podstromů) vůbec nevadí. Když je druhé optimum ve více barvách, tak je to jedno, protože jeho index využíváme až při rekonstrukci, a tedy optimum bude stejné. Když je stejné první a druhé optimum, tak při jakékoliv barvě předka bude použita tato hodnota, a tedy je jedno, jaký index bereme za optimální.
Takto spočteme minimum pro celý strom. Zrekonstruovat řešení pak již není problém. Od kořene budeme určovat barvy vrcholů: Pro kořen je to optimální barva a pro všechny ostatní vrcholy je to optimální barva za předpokladu, že předek má jinou barvu. V opačném případě je to druhá nejlepší barva.
Časová složitost je O(N+B log B), kde N značí počet vrcholů a B počet barev, protože musíme barvy setřídit dle hodnoty. Dále je již algoritmus lineární, protože v každém vrcholu uděláme maximálně lineárně operací vzhledem k počtu přímých potomků. Každý vrchol je nejvýše jednou přímým potomkem, tedy celkem to je O(N).
Další drobné zrychlení
 Ukážeme si, jak se zbavit logaritmu:
Nejprve si spočteme, kolik barev má smysl vůbec použít:
Na to, abychom u nějakého vrcholu počítali i-tou barvu,
musí daný vrchol mít i-2 potomků s různými optimálními barvami.
Tedy minimálně s barvami 0,1,2,…,i-2.
Nechť f(i) značí minimální počet vrcholů
podstromu, aby bylo nutné počítat i-tou barvu.
Z předchozí úvahy tedy musí platit
f(i)>f(0)+f(1)+...+f(i-2).
Ukážeme si, jak se zbavit logaritmu:
Nejprve si spočteme, kolik barev má smysl vůbec použít:
Na to, abychom u nějakého vrcholu počítali i-tou barvu,
musí daný vrchol mít i-2 potomků s různými optimálními barvami.
Tedy minimálně s barvami 0,1,2,…,i-2.
Nechť f(i) značí minimální počet vrcholů
podstromu, aby bylo nutné počítat i-tou barvu.
Z předchozí úvahy tedy musí platit
f(i)>f(0)+f(1)+...+f(i-2).
Označme i-tý člen Fibonacciho posloupnosti jako F(i). Dále nahlédneme, že musí platit, že f(i) ≥ F(i). Fibonacciho posloupnost totiž lze definovat i jako F(i) = F(0)+F(1)+...+F(i-3)+F(i-2). Stačí si uvědomit, že všechny členy až na poslední jsou z té samé definice pro i-1 rovny F(i-1), tedy to lze přepsat na známou definici F(i) = F(i-1)+F(i-2). Indukcí lze ukázat, že pro každé i musí být f(i) alespoň tak veliké jako F(i).
Pro to, abychom museli počítat barvu i, musí mít strom alespoň F(i) vrcholů. Počet potřebných barev tedy určíme tak, že najdeme index nejvyššího Fibonacciho čísla, které není větší než počet vrcholů. Maximální počet nutných barev označme M.
Bude nám stačit pouze najít nejlevnějších M barev a další už jsou nepodstatné a nemusíme je tedy ani třídit.
V lineárním čase vzhledem k B si vytvoříme minimovou haldu na všechny hodnoty. Pak z ní jen odebereme požadovaný počet nejmenších prvků, každý v logaritmickém čase vzhledem k B.
Odebírání z haldy má složitost O(M log B). To je ale méně než O(M2 + log 2 B), protože podle toho, zda-li je větší log B nebo M, tak se náš součin zvládne schovat do jednoho nebo do druhého sčítance. Jelikož Fibonacciho čísla rostou rychleji než libovolná polynomiální funkce, tak O(M2) náleží O(N). Také evidentně O(log 2 B) náleží O(B). Tedy O(M2 + log 2 B) je rychlejší než než O(N+B).
Celková časová složitost tedy bude chtěných O(N+B).
Stavba haldy
V předchozí argumentaci jsme předpokládali, že haldu s B prvky jsme schopní vytvořit v čase O(B). To je ale poměrně silné tvrzení, a tak by se slušelo ukázat, jak se to vlastně dělá.
Haldu budeme ukládat standardním způsobem v poli indexovaném od jedničky. Pro i-tý prvek tedy platí, že jeho potomci jsou na indexech 2i a 2i+1. Jeho předek pak na ⌊i/2⌋.
Do tohoto pole načteme v zatím neupraveném pořadí všechny požadované hodnoty. Až poté se z nich pokusíme vytvořit haldu.
Pole pak budeme procházet od konce. Když narazíme na prvek, který bude větší než alespoň jeden z jeho potomků, tak se ho pokusíme správně uložit. Prohodíme ho s menším z potomků. Tím se ale může rozbit haldová podmínka o úroveň níž. Proto takovéto prohození budeme s daným prvkem opakovat až do té doby, kdy už buď nebude mít žádné potomky a nebo budou větší než on.
Dále předpokládejme, že B je mocninou dvojky bez jedné. Lze to totiž zařídit doplněním nejvýše B prvků +∞. Počet prvků vzroste jen konstantně-krát. V takovémto případě má halda plně obsazené všechny úrovně.
Dá se ukázat, že počet prohození bude O(B). Každý prvek totiž může způsobit maximálně tolik prohození, na kolikáté úrovni od zdola se původně nacházel. Ve vyšších úrovních už ale není moc prvků, protože velikost úrovní se rychle zmenšuje.
Indukcí přes počet úrovní snadno ukážeme, že počet prohození může být nejvýše počet prvků. Když máme haldu o X úrovních, tak obsahuje 2X-1 prvků. Přidáním další úrovně přidáme 2X prvků. Tyto prvku jsou ve spodní úrovni, tedy nebudou vytvářet prohazování. Původní prvky se ovšem posunou o jednu úroveň od spodní výše, tedy každý z nich může vynutit o jedno prohození více. K maximálnímu počtu prohození 2X-1 v haldě o hloubce X tedy přibude nejvýše 2X-1 dalších prohození, což je stále méně než počet prvků 2X-1+2X. Počet prohození tedy nebude větší než počet prvků. Díky tomu bude složitost vytváření haldy skutečně O(B).
 32-5-3 Bomberman uklízí efektivně (Zadání)
32-5-3 Bomberman uklízí efektivně (Zadání)
Tato úloha navazuje na začátečnickou 32-Z4-4 (Bomberman uklízí). V jejím řešení ukazujeme snadný algoritmus, který mapu N×N vyčistí pomocí O(N3) kroků. Zvládnout to pomocí O(N2) kroků, tedy lineárně s velikostí mapy, už ale je úloha hodná hlavní kategorie.
Ze začátečnické úlohy se nám bude hodit zejména pozorování, že prohledávání do hloubky (DFS) projde celou mapu na O(N2) kroků. Navíc se ale při odbuchování trosek musíme schovávat do úkrytů. Takže si musíme úkryty naplánovat tak, abychom se k nim moc nenachodili.
DFS upravíme tak, aby střídalo osy (vodorovnou a svislou). Vždy si vybere jednu osu, projde všechna políčka dosažitelná oběma směry v této ose a odbouchne přitom všechny trosky, které mu leží v cestě. Pak se podívá na všechny odbočky od této osy a spustí se na ně rekurzivně s kolmou osou. Pozor na to, že odbočka může být zatarasena troskami – v tomto případě před tím, než do odbočky vlezeme, trosky odbouchneme.
Nyní algoritmus popíšeme přesněji. Při vstupu do rekurzivní funkce bude platit následující invariant:
- Stojíme na volném políčku X a máme určenou nějakou osu.
- Alespoň jedno sousední políčko ve směru této osy je volné (tomuto políčku budeme říkat B).
- Alespoň jedno sousední políčko v kolmém směru je volné (z jednoho takového jsme přišli a budeme mu říkat U).
- O pokračování prohledávání v kolmém směru ze vstupního políčka se postará ten, kdo nás zavolal.
Situace tedy bude vypadat nějak takto (o políčku označeném ? nepředpokládáme
vůbec nic, stará se o něj volající):
##*##*###U######
#.***..*BX*..**#
#####*###?###*##
1. fáze: likvidace překážek ve směru osy: Podíváme se podél osy v obou jejích směrech až k nejbližší zdi (okraj mapy také považujeme za zeď). Nikam přitom nechodíme, jen zkoumáme mapu. Kdykoliv najdeme trosky, postaráme se o jejich likvidaci. Dojdeme na sousední políčko B, položíme tam bombu, pak se schováme do úkrytu U, vydáme příkaz k odpálení, a nakonec se vrátíme na výchozí políčko. Tento „taneček“ spotřebuje konstantně mnoho kroků a zbaví nás minimálně jedněch trosek. Proto všemi tanečky za celou dobu algoritmu strávíme O(N2) kroků.
Situace z obrázku se změní takto:
##*##*###U######
#........X.....#
#####*###?###*##
2. fáze: uvolňování vchodů do odboček: Uvolnili jsme „chodbu“ v aktuální ose. Teď chceme odklidit všechny trosky bránící přístupu do odboček a také se na každou odbočku rekurzivně zavolat (povšimněme si, že invariant bude opět platit). Chodbu už procházíme doopravdy. Kdykoliv vedle aktuálního políčka P leží trosky, položíme bombu na P, odejdeme se schovat do úkrytu, odpálíme ji a vrátíme se na P. Poprvé jako úkryt použijeme políčko U, každým uvolněním odbočky vytvoříme nový úkryt, který bude k další odbočce blíž než U. Celkem tedy v každém směru na cestách do úkrytů projdeme každé políčko konstanta-krát. Takže za celou dobu běhu algoritmu strávíme ukrýváním se O(N2) kroků.
Inicializace: Zbývá dořešit zdánlivou maličkost: Jak celé DFS rozeběhnout, aby od začátku platil invariant? K tomu si pořídíme další, „zahřívací“ DFS. To bude chodit pouze po volných políčkách (nebude rozlišovat trosky od zdí) a zastaví se v okamžiku, kdy navštíví trojici po sobě jdoucích políček tvořících tvar „L“. Pokud by v mapě žádné L nebylo, znamená to, že volná políčka dosažitelná ze startu tvoří jedinou rovnou chodbu. Tehdy se trosky (existují-li nějaké) určitě nedají uklidit.
Takže máme L. Postavíme se do jeho středu, vybereme si osu jednoho z ramen a všimneme si, že v tomto okamžiku je invariant splněn. Můžeme tedy zavolat hlavní DFS. Ale pozor, v ose druhého ramene ještě mohou zbýt neuklizené trosky. Zavoláme proto hlavní DFS ještě jednou v kolmé ose.
Celkem tedy strávíme O(N2) kroků zahřívacím DFS a dalších O(N2) každý ze dvou hlavních DFS. Máme tedy řešení lineární ve velikosti mapy.
Dodejme ještě, že náš vzorový program z nalezené cesty „vystříhává“ dvojice kroků, které jsou k sobě inverzní. Pak cesta vůbec nezalézá do odboček, kde není potřeba nic odpálit. Tím se například celé zahřívací DFS redukuje na projití jedné cesty od počátku k nalezenému L.
 32-5-4 Distribuované počítání (Zadání)
32-5-4 Distribuované počítání (Zadání)
Úlohu můžeme lehce zobecnit. Nechť základen je L a místo mediánu hledáme M-tý prvek. Naším cílem je minimalizovat počet poslaných zpráv. Je několik způsobů, jak jich poslat logaritmicky mnoho (tj. O(log N)), jeden si ukažme:
Každá základna si nejprve setřídí svých N čísel a poznamená si, jaký jejich rozsah může obsahovat medián. Ze začátku je to všech N prvků. Protokol pak bude pracovat po iteracích. V každé iteraci nejprve základna s nejdelším uvažovaným rozsahem pošle prostřední prvek x tohoto rozsahu. Ostatní základny odpoví, kolik jejich čísel je nižších (což mohou zjistit například pomocí binárního vyhledávání). Tím zjistíme, kolikáté v pořadí x celkově je. Je-li M-té, máme vyhráno. Jinak si všechny základny upraví svůj uvažovaný rozsah. Pokud je pořadí x nižší, než M, ještě nižší prvky nemá smysl uvažovat a tak je z rozsahů odebereme. Pro pořadí x převyšující M postupujeme naopak. Tím iterace končí.
| 1 |
| 2L |
| 2L |
| 2L-1 |
Musíme ještě dořešit pár implementačních detailů. Pokud v některé iteraci (např. nutně v té první) má maximální délku rozsahu D více základen, vybereme tu s nejnižším indexem, nebo případně necháme prostřední prvek poslat všechny tyto základny a jako určující hodnota se jednoznačně vybere nejnižší z těchto hodnot (nebo třeba medián). A všimněme si, že všechny základny vždy znají délky rozsahů uvažovaných všemi ostatními. Ze začátku je to všech N hodnot a v každé iteraci nám základny prozradí, jakou část rozsahu odstraňují.
I kdyby nebylo zvlášť těžké takový protokol naimplementovat, popis stál trochu úsilí. Logaritmicky ale funguje taky úplně jednoduché řešení, kdy M-tý prvek binárně vyhledáváme postupně ve všech základnách, dokud na něj nenarazíme (tj. každá základna si při bin. vyhledávání nechává od ostatních posílat, kolik hodnot je nižších a pokud přímo M-tý prvek nenajde, na řadu přijde další základna).
 Naše vzorové řešení funguje hezky pro malý počet základen. Ale pokud máme
základen hodně, základ logaritmu se přiblíží ošklivě blízko k jedničce.
Například pro L=10 je to 20/19≐1.05. To už dá cca 14-krát větší
logaritmus, než je dvojkový.
Naše vzorové řešení funguje hezky pro malý počet základen. Ale pokud máme
základen hodně, základ logaritmu se přiblíží ošklivě blízko k jedničce.
Například pro L=10 je to 20/19≐1.05. To už dá cca 14-krát větší
logaritmus, než je dvojkový.
Situaci zachrání randomizace: místo abychom zvolili x jako medián základny s nejvíce prvky, vybereme ho rovnoměrně náhodně ze všech prvků všech základen. K tomu využijeme, že známe počty prvků jednotlivých základen. Rozdělíme proto interval od 1 do aktuálního počtu prvků na podintervaly velké podle základen. Pak vygenerujeme rovnoměrně náhodné číslo ve velkém intervalu. To, do kterého podintervalu číslo padlo, nám určí základnu. A pozice uvnitř podintervalu nám řekne, kolikáté nejmenší číslo z této základny to má být.
Tak požádáme základnu, ať nám toto číslo řekne. Pak se zeptáme všech ostatních základen, kolik jejich čísel je menších. To nám umožní udělat stejný krok jako v předchozím algoritmu.
Na rozdíl od předchozího algoritmu ovšem víme, že v průměru odstraníme aspoň jednu polovinu celkového počtu prvků. Průměrný počet kroků proto bude O(log LN), přičemž základ logaritmu tentokrát nezávisí na počtu základen L. Jeden krok zahrnuje poslání L zpráv, takže celkový počet zpráv bude O(L log LN).
Algoritmus by si zasloužil poctivější analýzu. Pokud jste zvědaví, jak se to udělá, podívejte se na kapitolu o randomizaci v Průvodci labyrintem algoritmů, konkrétně rozbor algoritmu Quickselect.
 32-5-5 Druhá kostra (Zadání)
32-5-5 Druhá kostra (Zadání)
Na tuto úlohu existuje jednoduché řešení, na které nebylo těžké přijít, a pak také o něco složitější, ale daleko rychlejší řešení. Obě jsou založená na prohazování hran v kostře, což intuitivně dává smysl a v open-datovce není potřeba dokazovat správnost. Zde se nicméně do teorie okolo koster ponoříme trochu hlouběji a vše poctivě odvodíme.
Při budování teorie nám bude pomáhat, že váhy všech hran jsou navzájem různé. Kdyby nebyly, algoritmus by také fungoval, ale důkaz jeho správnosti by byl náročnější.
Výměny hran
Začneme následující úvahou: mějme nějakou kostru K a hranu e, která v kostře neleží. Koncové vrcholy hrany e jsou v kostře K spojené nějakou cestou, které budeme říkat K[e] (tato cesta je určena jednoznačně, neboť K je strom).
Pokud do kostry K přidáme hranu e, vznikne kružnice K[e]+e. Tu můžeme rozpojit smazáním libovolné hrany f∈K[e] a vznikne opět nějaká kostra. Označíme ji K' = K + e - f. Její váhu spočítáme snadno (w(… ) budeme značit váhu):
Této operaci říkáme výměna hrany e za hranu f.
Pokud k hraně e (přidávaná hrana) umíme najít f∈K[e] (odebíraná hrana) tak, aby bylo w(e) < w(f), bude nová kostra K' lehčí než původní K. Tehdy říkáme, že e je lehká hrana vzhledem ke kostře K, neboli K-lehká hrana. Pokud byla kostra K minimální, nemůžeme ji nijak zlepšit, takže nemohou existovat žádné K-lehké hrany.
Situaci ilustruje následující obrázek. Černě je vyznačena kostra K, šedivě kostra K', tučně cesta K[e]:
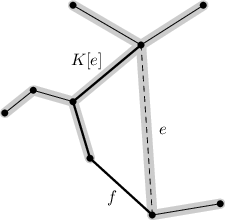
Pomocí výměn jde dokonce z libovolné kostry udělat libovolnou. Platí následující dvě tvrzení:
Vyměňovací lemma: Nechť K a K' jsou dvě kostry téhož grafu. Pak existuje posloupnost výměn (pokaždé jednu hranu přidáme a jednu ubereme), která z K vyrobí K'.
Monotónní vyměňovací lemma: Nechť K a K' jsou dvě kostry téhož grafu a neexistují žádné K-lehké hrany. Pak existuje posloupnost výměn, která z K vyrobí K' a v každém kroku váha kostry vzroste.
Obě lemmata dokážeme na konci řešení. Teď z nich odvodíme několik důsledků:
- Nejlehčí kostra je jednoznačná. Mějme dvě nejlehčí kostry K a K'. Můžeme na ně použít monotónní lemma (neboť k minimální kostře neexistují lehké hrany). Kdyby K byla různá od K', posloupnost výměn by obsahovala aspoň jeden krok. Jelikož každým krokem váha roste, muselo by být w(K) < w(K'), takže K nemohla být nejlehčí.
- Už víme, že k nejlehčí kostře neexistují lehké hrany. Platí to i naopak: Kostra, k níž neexistují lehké hrany, je už nejlehčí. Použijeme monotónní lemma na kostru bez lehkých hran K a nejlehčí kostru K'. Opět kdyby K byla různá od K', muselo by platit w(K) < w(K'), což nejde. Tohle k řešení nebudeme potřebovat, ale hodí se to vědět – znamená to, že k definici nejlehčí kostry vůbec nepotřebujeme váhy hran sčítat, stačí je umět porovnávat.
- Teď to hlavní: Druhá nejlehčí kostra se liší od nejlehčí právě jednou výměnou. Monotónní lemma použijeme na nejlehčí kostru K a druhou nejlehčí K'. Lemma slibuje nějakou posloupnost výměn. Kdyby v ní byla více než jedna výměna, tou první z nich bychom se dostali do nějaké kostry K*, která je těžší než K, ale lehčí než K'. Takže K' nemohla být druhá nejlehčí.
Jednoduchý algoritmus
Náš algoritmus začne nalezením nejlehčí kostry K. Spustíme třeba Kruskalův algoritmus z kuchařky, který poběží v čase O(M log N), kde N je počet vrcholů a M počet hran.
Pak budeme postupně probírat všechny hrany f, které neleží v nejlehčí kostře K. Pro každou z nich budeme hledat výměny: najdeme cestu v K spojující koncové vrcholy hrany f. To zvládneme třeba prohledáním kostry do šířky z jednoho koncového vrcholu. Na této cestě pak najdeme nejtěžší hranu e, což je ta, kterou budeme chtít vyměnit s f. Výměnou vznikne nějaká kostra, ale ani ji nebudeme konstruovat, stačí si uvědomit, že její váha je w(K) + w(f) - w(e).
Jak už víme, mezi sestrojenými kostrami bude druhá nejlehčí. A bude to ta nejlehčí z nich.
Určíme časovou složitost: zkoušíme nanejvýš M hran mimo kostru, pro každou z nich hledáme cestu v kostře v čase O(N) (každá kostra má N-1 hran, viz níže) a pak na této cestě v čase opět O(N) najdeme maximum. Celkem tedy algoritmus doběhne v čase O(M log N + MN) = O(MN).
Rychlý algoritmus
Jde to pochopitelně i rychleji: pro nejlehčí kostru si předpočítáme datovou strukturu, která bude umět rychle odpovídat na otázky typu „Jaká je nejtěžší hrana na cestě mezi těmito dvěma vrcholy?“.
Šikovnou datovou strukturu pro tento typ dotazů získáme pomocí dekompozice stromu na lehké a těžké hrany neboli heavy-light dekompozice. Tu najdete popsanou v našem seriálu o stromech z 29. ročníku, konkrétně v úloze 29-4-7 a jejím řešení. (Pozor, lehké hrany v dekompozici nemají nic společného s lehkými z teorie minimálních koster. Nebo aspoň o takové souvislosti nevíme.)
Strukturu vybudujeme v čase O(N) a na každý dotaz nám pak odpoví v čase O(log N). Tím pádem zvládneme každou hranu mimo kostru vyzkoušet v čase O(log N) a celý algoritmus poběží v čase O(M log N + N + M log N) = O(M log N).
Dodejme, že optimální prohození jde pomocí mnohem sofistikovanější datové struktury nalézt i v lineárním čase. Přiznáváme, že má spíš teoretický význam, protože konstanty skryté v O jsou obrovské. Pro libovolnou praktickou velikost grafu tedy bude rychlejší náš algoritmus. Navíc stále potřebujeme najít nejlehčí kostru. Kdybyste i přesto byli zvědaví, jak se to dělá, ulovte si na soustředění Medvěda :)
Důkaz prosím
 Teď slíbený důkaz obou lemmat. Inspirujeme se kapitolou o minimálních kostrách
z knížečky Krajinou grafových algoritmů.
Teď slíbený důkaz obou lemmat. Inspirujeme se kapitolou o minimálních kostrách
z knížečky Krajinou grafových algoritmů.
Nejprve si všimneme, že kostry téhož grafu se liší pouze množinou hran, takže je často budeme za množiny hran považovat. Dokonce jsou to vždy stejně velké množint hran, neboť každý strom s N vrcholy má N-1 hran (to můžeme dokázat indukcí odtrháváním listů).
Jak moc se kostry K a K' liší, budeme měřit velikostí jejich symetrického rozdílu |KΔK'|. Symetrický rozdíl dvou množin obsahuje ty prvky, které leží v právě jedné z množin. Tedy AΔB = (A∪B) \(A∩B). Jelikož |A∪B| = |A| + |B| - |A∩B|, máme |AΔB| = |A| + |B| - 2|A∩B|. Takže pokud A a B mají stejný počet prvků (jako třeba množiny hran dvou koster), velikost symetrického rozdílu musí být sudá.
Vyměňovací lemma dokážeme snadno indukcí podle „vzdálenosti“ koster |KΔK'|. Je-li nulová, K=K' a není potřeba žádná výměna.
Nyní indukční krok. Je-li K různá od K' a obě mají stejný počet hran, musí existovat hrana e', která leží v K', ale neleží v K (značíme e'∈K'\K). Podle pozorování o výměnách musí jít vyměnit za nějakou hranu e∈K\K'. Tím dostaneme nějakou kostru K*, která je „blíž k K', než byla K“. Přesněji |K*ΔK'| = |KΔK'| - 2, protože jak e, tak e' ležely v symetrickém rozdílu.
Tím pádem můžeme použít indukční předpoklad, aby za naši jednu výměnu doplnil posloupnost výměn, která z K* udělá K'.
Nyní indukci vylepšíme, aby z ní vyšlo monotónní vyměňovací lemma. Pokud vyměňujeme e∈K\K' za e'∈K'\K, nemůže tím váha kostry klesnout – kdyby klesla, znamenalo by to, že w(e') < w(e), takže e' by byla K-lehká hrana. A takové podle předpokladů lemmatu neexistují. Navíc váha kostry nemůže ani zůstat stejná, protože váhy hran jsou navzájem různé.
První výměna v posloupnosti je tedy rostoucí. Teď bychom chtěli použít indukční předpoklad na sestrojení zbytku posloupnosti. Ale ouha: Na to bychom potřebovali zaručit, že ani k nové kostře K* neexistují lehké hrany. Přesněji řečeno, stačilo by, kdyby žádné takové nebyly v K'\K*, neboť to jsou jediné hrany, které v našem důkazu využíváme.
Pro obecnou volbu hrany e'∈K'\K by to nicméně nemuselo platit. Ale pomůžeme si tak, že za e' zvolíme nejlehčí ze všech hran v K'\K.
Nyní uvažujme libovolnou hranu f∈K'\K*, o níž chceme dokázat, že není K*-lehká. Má tedy být těžší než všechny hrany na cestě K*[f] spojující v K* koncové vrcholy hrany f. Pro cestu K[f], která spojuje tytéž vrcholy v K, to podle předpokladů platilo. Jak se tedy může K*[f] lišit od K[f]?
- Pokud enot∈K[f], vyskytuje se cesta K[f] i v K*, takže musí být K*[f] = K[f] a je vyhráno.
- Nebo e∈K[f], takže K*[f] musí smazanou e někudy obejít. Tehdy K[f] jistě
prošla po nějakém oblouku kružnice C = K[e']+e' (protože e∈K[e']). Takže z kružnice C
využijeme opačný oblouk – tedy ty hrany, které jsme nevyužívali předtím. Jinými slovy
K*[f] = K[f]ΔC. Proto hrany, které přibyly na K*[f], jsou lehčí než e'
(protože e' nebyla K-lehká) a ta je lehčí než f (díky volbě e' jako nejlehčí z K'\K).
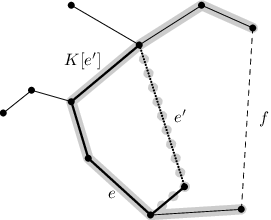
Poněkud nepřehlednou situaci mapuje obrázek níže: černě je vyznačena kostra K, šedivě cesta K[f] a šedivě tečkovaně „objížďka“ po tučné kružnici K[e'] + e'.
Tím pádem žádná hrana f není K*-lehká a indukce může běžet dál.
Poznámka: Vyměňovací lemmata jsou mnohem mocnější nástroj. Například z nich snadno dostaneme, že třetí nejlehčí kostra vznikne jednou výměnou buď z nejlehčí nebo z druhé nejlehčí. Takto se dá pokračovat a odvodit algoritmus na nalezení k-té nejmenší kostry.
 32-5-6 Geocaching s odhadem (Zadání)
32-5-6 Geocaching s odhadem (Zadání)
Nejprve je dobré si udělat alespoň nějakou představu, s jakými daty vlastně pracujeme. Vhodné je mapu si například rozdělit na čtverečky a u každého se zeptat, kolik je v něm obyčejných a prémiových kešek.
Toto je možný výsledek: Každé políčko představuje čtvereček o velikosti 0.05°×0.05°. Číslo v něm je počet normálních keší. Modrá barva značí jednu prémiovou keš a červená dvě a více.
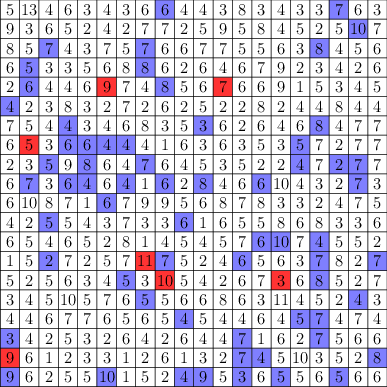
Dále předpokládejme, že podobně mapa vypadá všude a při jakémkoliv tokenu.
Z obrázku lze vypozorovat hned několik věcí. Například, že v libovolném čtverci 0.2°×0.2° by téměř vždy mohla existovat alespoň jedna prémiová keš a současně by v něm nemuselo být více než 500 keší.
V našem algoritmu tedy začneme s takto velikým čtvercem a pokusíme se najít všechny prémiové kešky v něm. Když najdeme všechny, tak se posuneme do dalšího čtverce.
Na hledání lze použít binárního vyhledávání. Každým dotazem zmenšíme plochu, kde může keš ležet na polovinu. Po dostatečném počtu kroků skončíme s malým čtverečkem, u kterého stačí říct, že keš je uprostřed a vždy budeme v toleranci.
Jak ale binárně vyhledávat na dvojrozměrné ploše? Můžeme střídat kroky dvojího druhu. Buď plochu ořízneme vertikálně, nebo horizontálně. V každém kroku tedy určíme dva obdélníčky. Na jeden z nich se zeptáme. Podle toho, zda v něm hledaná keš je, si zvolíme obdélníček do dalšího kroku. Jelikož víme, že keš leží alespoň v jednom z nich, tak v případě, že není v jednom, musí být v druhém.
Po 28 krocích skončíme s čtverečkem velikosti 0.000014°×0.000014°. Ten již je dostatečně malý.
Když máme v jednom původním čtverci více než jednu prémiovou keš, můžeme vyhledávat každou zvlášť. Lepší ale je počítat společnou část vyhledávání pouze jednou.
Hledání lze implementovat jako rekurzivní funkci. Ta bude jako parametry brát prohledávaný obdélníček, směr, v němž se má oříznout, a seznam prémiových keší v něm. Po dotazu do api se pak sama zavolá na ty obdélníčky, kde je alespoň jedna keš.
Jelikož na získání jedné keše by nemělo být potřeba více než 29 dotazů, na povolený počet jich zvládneme získat alespoň 172. Naše implementace tohoto algoritmu jich zvládne většinou okolo 180.
Chceme více keší!
Povšimneme si, že naše vyhledávání není optimální. Vždy, když se ptáme api na nějaký čtverec, tak nás vlastně zajímá, kterým směrem leží keše od jedné z tázaných stran. Vůbec ale nevyužíváme ostatní tři strany. Pojďme to napravit.
Nejprve si vytvoříme takovou přehledovou plánovací mapu. Něco podobného obrázku na začátku tohoto řešení.
Ptát se na každý čtvereček by nás stálo moc dotazů. V každém čtverci 1°×1° se proto budeme ptát pouze na celé sloupce a celé řádky. Pro každou keš pak určíme, ve kterém průsečíku leží.
Další drobnou optimalizaci lze učinit tím, že se budeme ptát na mírně překrývající se sloupce (resp. řádky). Z toho budeme vědět, zda keš leží v překryvu či nikoliv.
Polohu každé keše dále budeme vyhledávat zvlášť v každé souřadnici. Tedy místo jedné keše si můžeme představit dvě hledané pozice. Jednu v horizontálním a jednu ve vertikálním směru.
Dále se pokusíme rozdělit hledané pozice do čtveřic, ve kterých je pak budeme vyhledávat. V každé čtveřici musí platit:
- Obsahuje dvě horizontální a dvě vertikální hledané pozice
- Lze je vyhledávat obdélníkem. Tedy jedna vertikální leží výše než obě horizontální a druhá níž. To stejné i pro horizontální.
- Obdélník ohraničující danou čtveřici obsahuje nejvýše 499 keší (včetně prémiových).
- Ani v jedné souřadnici tento obdélník není delší než 1°.
Jelikož rozdělení všech hledaných pozic pouze do čtveřic je nereálné, zbylé hledané pozice pak umístíme i do trojic, dvojic, nebo nejhůře je necháme samotné. Budeme se ale snažit, aby těchto skupin bylo co nejméně.
Jelikož toto nejspíš ani nelze dělat žádným rozumně rychlým algoritmem, vystačíme si s hladovým řešením. To nás k optimu dostatečně těsně přiblíží.
V naší implementaci jsme zkoušeli ke každé zatím nepoužité vertikální pozici vzít dvě nejbližší horizontální pozice. Jednu ve směru nahoru doprava a druhou dolů doprava. Od nich vpravo výškou mezi nimi se pak pokoušíme najít vyhovující zakončení.
Tento algoritmus pak ještě vyzkoušíme pro všechny možnosti otočených souřadnic.
Zbylé hledané pozice pak vyzkoušíme stejným způsobem rozdělit do trojic a pak i dvojic.
Když už máme rozdělené skupinky, každou můžeme zkusit vyhledávat.
Prostě se budeme ptát na obdélník, který bude omezen z každé strany polovinou z vyhledávaných pozic. Každou z čtveřice vyhledávaných pozic tímto omezíme na příslušnou polovinu podle toho, zda odpovídající keš leží v tázaném čtverci.
Tímto algoritmem lze dospět za povolený počet dotazů až k 820 keším.