Třetí série třicátého pátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 35-3-1: Čajovod
- 35-3-2: Hroší hortenzie
- 35-3-3: Prodlužovačky
- 35-3-4: Záchrana listí
- 35-3-S: Vektorové prostory
- 35-3-X1: Obvody
 35-3-1 Čajovod (Zadání)
35-3-1 Čajovod (Zadání)
Nejprve si rozmysleme lehčí variantu, v níž neexistují manažeři. Určitě pak nemá smysl nějaké kohouty zavírat – nepomůže nám to a spotřebujeme tah navíc. Můžeme tedy ignorovat nejen prázdné místnosti, ale i programátory, k nimž aktuálně čaj proudí. Pro ty na suchu zase existuje jednoznačná množina kohoutků, které musíme otevřít (každé 2 vrcholy ve stromu spojuje právě jedna cesta).
Jak je najít? Nabízí se využít rekurzivní struktury stromu a prohledat jej do
hloubky. Pro každý vrchol si zjistíme, jestli se v jeho podstromu nachází
místnost s programátory. V listech to je ANO pro programátory
a NE pro prázdnou místnost. Ve vnitřních vrcholech spočítáme logickou
disjunkci (tzv. or) z potomků. Jestliže je kohoutek na nějaké hraně zavřený
a zároveň vrchol, do kterého hrana vede, obsahuje programátory v podstromu, otevřeme jej.

Proč nám tento postup nefunguje pro vstupy s manažery? Pořád přeci platí, že všechny kohoutky na cestách k programátorům musí být otevřené. Jenže pro manažery je situace jiná. Stačí zavřít jeden kohoutek na cestě k nim, máme tedy na výběr. Chceme zvolit takovou variantu, která povede na nejmenší počet změn.
Všechny varianty vyzkoušet nemůžeme, je jich Θ(2N). Budou ale často sdílet společné části a i náš výpočet bude pořád dokola rozmýšlet optimální řešení téhož podstromu, akorát pro jiné způsoby řešení předků. Co takhle si mezivýsledky ukládat? Různých podstromů je přeci jen N. Tento způsob zrychlení algoritmu se obvykle nazývá dynamické programování.
Stále budeme používat DFS. Náš plán bude pro každý vrchol spočítat, kolik nejméně změn v podstromu potřebujeme provést. Toto navíc spočítáme pro dva případy: pokud do vrcholu čaj přitéká a pokud ne. Pokud v daném případě nelze splnit podmínky (například by dotekl čaj k manažerům), jako počet změn použijeme nekonečno.
Jakmile tuto informaci známe pro všechny syny daného vrcholu, můžeme zpracovat vrchol samotný. Projdeme všechny hrany, které z vrcholu vedou, a pro každou se rozhodneme, jestli je výhodnější její stav změnit nebo ne. Nakonec sečteme změny na všech hranách i v jejich podstromech a součet uložíme do vrcholu, abychom tuto hodnotu mohli použít, až budeme zpracovávat rodiče.
Jakou časovou složitost máme teď? Každý vrchol zpracujeme jen jednou, poté jednou použijeme hodnoty uložené v něm. Časová složitost je proto O(N). Obdobně paměťová, pořídili jsme si navíc jen dvě počítadla na každý vrchol.
Poznámka k implementaci: Jako vhodné nekonečno pro tahy, které nesplňují podmínky, můžeme zvolit třeba N, neboť více tahů se ani udělat nedá.
 35-3-2 Hroší hortenzie (Zadání)
35-3-2 Hroší hortenzie (Zadání)
Problém můžeme reformulovat tak, že pro každý z N intervalů koncentrací (které chtějí kamarádi pít) chceme nalézt nejlevnější (co do počtu lístků) mističku, která dokáže vytvořit koncentraci v tomto rozpětí.
Fakt, že koncentrace mohou být opravdu velké, nám úlohu trochu komplikuje, avšak můžeme si povšimnout, že potřebujeme jen malý zlomek těchto hodnot. V podstatě nás zajímají jen hodnoty koncentrací misek, abychom mohli určit, kterou misku použijeme. A protože našich mističek je pouze K, můžeme přečíslovat celý rozsah koncentrací na čísla 1 až K. To uděláme tak, že seřadíme mističky podle koncentrací vzestupně a přiřadíme jim čísla (indexy) 1 až K. Pak postupně přečíslujeme všech N požadovaných intervalů, aby interval popisoval rozsah indexů mističek, ve kterých může Lucka danému kamarádovi připravit čaj. Přečíslování zvládneme rychle binárním vyhledáváním.
Nyní pojďme vyřešit zbytek úlohy. Pro každý z N intervalů chceme udělat minimový dotaz, tedy chceme zjistit mističku z tohoto intervalu, na kterou potřebujeme minimum lístků. K tomu využijeme intervalový strom. Pokud intervalové stromy neznáte, podívejte se do naší kuchařky.
Sestavíme si intervalový strom obsahující všechny mističky, přičemž se budeme dotazovat na minimum potřebných lístků. Tedy nám stačí udělat N dotazů, z nichž každý zabere O(log K) času, celkově tedy O(N log K).
Ještě však musíme zvážit původní přečíslování, které nám zabralo O(N log K) (N binárních vyhledání v K mističkách) a také na začátku musíme intervalový strom sestavit, to však zabere maximálně O(K log K) času.
Tedy celková složitost je O(N log K).
 35-3-3 Prodlužovačky (Zadání)
35-3-3 Prodlužovačky (Zadání)
Úlohu budeme řešit po patrech odspoda, tedy začneme v patře stromu s nejvyšší hloubkou a postupně budeme spravovat vrcholy na vyšších a vyšších hladinách, až dorazíme do kořene, který je určitě v pořádku – zeď má neomezenou kapacitu.
Buďme v nějakém vrcholu v a předpokládejme, že v celém odpovídajícím podstromu jsou již zařízení popřepojovány, aby odpovídající příkon byl nižší než daná kapacita, a zbývá nám opravit v.
Pokud součet příkonu v podstromu nepřesahuje kapacitu v, není třeba nic opravovat a můžeme pokračovat do vyšších pater. V opačném případě je potřeba odpojit nějaká zařízení v odpovídajícím podstromu – odpojování mimo podstrom nijak neovlivňuje příkon do v.
Předpokládejme, že známe, která ještě neodpojená zařízení odpovídají podstromu a zajímá nás, která z nich musíme odpojit, abychom opravili v.
Nechť k je minimální číslo takové, že v lze opravit k odpojeními. Pokud však dokážeme opravit v odebráním nějakých k zařízení z daného podstromu, tak určitě dokážeme v opravit odpojením těch k předmětů s největším příkonem. To však vede na jednoduchý způsob, jak opravit vrchol v – budeme odpojovat zařízení od toho s největším příkonem, dokud v neopravíme.

Tato myšlenka vede na následující algoritmus. V obráceném BFS pořadí budeme procházet všechny vrcholy a každý spravíme odebíráním neodebraných spotřebičů s největším příkonem.
Potřebujeme však ještě dokázat, že tento lokálně optimální algoritmus vrátí řešení, které je optimální i globálně. To však není těžké nahlédnout indukcí podle hladiny. V daném vrcholu v potřebujeme odebrat alespoň k zařízení – stejně jako pro v, tak i pro všechny jeho předchůdce však nikdy nebude na škodu vzít ty s největším příkonem. Pokud bychom jich chtěli vybrat více než k, pak jich můžeme vybrat jen k a ten zbytek později, až to bude potřeba. Tedy lokálně optimální výběr zachovává globální optimalitu.
Zbývá si tedy rozmyslet, jak algoritmus efektivně implementovat. V každém vrcholu potřebujeme hledat a odebírat minima a spojovat zařízení ze synů – tedy podporovat operaci slévání. Na to můžeme použít haldy, které podporují slévání – například binomiální (či Fibonacciho) haldu, kde slévání a odebírání minima umíme v logaritmickém čase. Algoritmus bychom pak mohli implementovat jako procházení v obráceném BFS pořadí, nebo jako DFS (můžeme si rozmyslet, že při DFS již rovněž známe všechna odebraná zařízení z podstromu).
A jaká je časová složitost? Každé zařízení odebereme nejvýše jednou a práci na slití v haldě můžeme naúčtovat synovi, celkem tak dostáváme linearitmickou složitost, tedy O(N log N).
Tento algoritmus je sice po teoretické stránce uspokojivý, neboť má příjemnou asymptotickou složitost, jeho implementace by ale byla složitější, neboť vyžaduje některou z pokročilých hald.
Místo haldy bychom mohli ale použít obyčejný binární vyhledávací strom a slévání dvou stromů implementovat tak, že prvky z menšího ze dvou stromů popřesouváme do většího. Kdybychom prvky nemazali, nebylo by složité nahlédnout, že každý prvek přesuneme O(log N)-krát. Tedy celková časová složitost by byla O(N log 2 N). Pokud prvky mažeme, každý prvek můžeme přesunout vícekrát, ale v každém kroku pracujeme jen s haldami, které nemají větší velikosti, než kdybychom prvky vůbec nemazali. To ale znamená, že provedeme nejvýše tolik práce a celková složitost tak zůstává O(N log 2 N).
 35-3-4 Záchrana listí (Zadání)
35-3-4 Záchrana listí (Zadání)
Lehká varianta
Nejdříve se podívejme, jak řešit jednoduchou variantu, a potom budeme zobecňovat. Představme si, že chceme víko přivázané k i-té krabici někam položit. V takové chvíli je jedno, zdali jsou na krabicích 0 až i-2 položená víka, protože tam provázek nedosáhne. Stačí tedy zohlednit krabice i-1 až i+1.To navádí na dynamické programování. Postupně budeme přidávat krabice a vždy si budeme pamatovat, kolik nejvíce listí umíme zachránit. Dle pozorování výše však kromě aktuální krabice musíme uvážit stav předešlé a následující krabice. Na každé z těchto tří krabic buď leží víko, nebo ne. Budeme si tedy pamatovat maximum pro každou z těchto kombinací. Pokud některá kombinace nemůže nastat (např. nemáme dost vík), pak si pro danou kombinaci zapamatujeme minus nekonečno.
Označme si dp[i][c] hodnotu pro kombinaci c s poslední krabicí na pozici i. Např. pokud v naší kombinaci víko na předchozí krabici položené není, aktuální je, a následující také je, značme ji dp[i][(0, 1, 1)].
Nyní bychom chtěli z hodnot pro kombinace končící na pozici i určit hodnoty pro kombinace na pozici i+1. Nejdřív posuňme všechny kombinace. To jen z naší kombinace vypadne levá krabice a vpravo přibude nová, zatím bez víka: (0, 1, 1) → (1, 1, 0). Nový stav mohl vzniknout ze dvou různých předchozích stavů, z nich vybereme ten lepší:
A pokud je k současné krabici přivázané víko, zkusíme jej postupně přidat na každou volnou krabici v naší kombinaci. Pokud takto najdeme nové maximum, použijeme jej pro nově vzniklou kombinaci.
Na závěr vybereme tu kombinaci, která nám dává nejvíce suchého čaje. A na to, abychom zjistili, kam víka dávat, můžeme použít obvyklý trik – pamatujeme si, jak jsme nové hodnoty kombinací volili, a jen jdeme pozpátku.
Pro K=1 bude výsledná časová složitost O(N).
Těžká varianta
Na těžkou variantu bychom si samozřejmě mohli udržovat všechny možné stavy, zdali příslušné krabice mají a nemají víko, těch je ale O(2K). Všimněme si ale, že můžeme vždy víka dát tak, aby se provázky ke krabicím nekřížily. Je to proto, že kdybychom prohodili zkřížená víka, zmenšíme vzdálenosti vík od krabic s provázkem, čímž nic nezkazíme.Díky tomu jsme schopni udržovat kombinace podle toho, kam jsme položili poslední víko. Posunutí krabic o jedna dozadu znamená pouze posunutí o 1 pozici zpátky.
Je-li k aktuální krabici přivázané víko, tak ho můžeme položit na kteroukoliv pozici za posledním víkem. Pro každou tuto pozici najdeme nejlepší z předešlých kombinací.
Ještě můžeme přidat jedno zrychlení, nejlepší kombinaci totiž nemusíme hledat pořád dokola. Vše zvládneme v jediném průchodu, nejlepší kombinaci stačí průběžně aktualizovat během toho, co zkoušíme pokládat víka.
Tím se dostaneme na výslednou časovou složitost O(NK), která stačí na plný počet bodů.
 35-3-X1 Obvody (Zadání)
35-3-X1 Obvody (Zadání)
Naivní řešení
Nejprve se pojďme zamyslet nad tím, jak by se úloha řešila v případě, že bychom pro každou pozici měli jen seznam povolených rezistorů, nikoliv tedy intervaly. Toto je vcelku standardní úloha, kterou lze řešit pomocí toků v síti. Pro každou pozici si vytvoříme vrchol napojený ze zdroje jednotkovou hranou. Každé z možných hodnot odporů vyrobíme vrchol připojený na stok taktéž jednotkovou hranou. Pak už jen přidáme hranu spojující každou pozici s na ní povoleným odporem. Na výslednou sít spustíme algoritmus, který nám najde maximální tok.
Pokud bude velikost toku stejná, jako počet pozic, tak snadno zvládneme zkonstruovat řešení. Přes každou pozici musí protékat jedna jednotka toku. Ta poteče dále do odporu. Ten použijeme na danou pozici. Jelikož má odpor jen jednu odtokovou hranu, tak jím může protékat nejvýše jedna jednotka toku, a tedy odpor může být použit v nejvýše jedné pozici. Řešení je tedy validní.
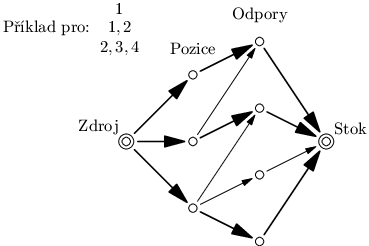
Dále se dá nahlédnout, že když řešení existuje, tak maximální tok musí mít velikost odpovídající počtu pozic na rezistory. Větší být evidentně nemůže, protože ze zdroje toho nemůže vytékat více. Podobně jako je popsané v předešlém odstavci, pokud bychom znali řešení úlohy, zvládli bychom zkonstruovat tok s velikostí počtu pozic. Maximální tok tedy nemůže být menší. Tedy když maximální tok není dostatečně velký, máme zaručeno, že řešení neexistuje.
Časová složitost takového řešení se odvíjí od použitého algoritmu na toky. Ten řešíme pro Θ(N+V) vrcholů a Θ(N+M+V) hran, kde N značí počet pozic na rezistory, M celkový počet intervalů (tedy součet délek seznamů povolených rezistorů v pozicích) a V je počet rezistorů, které lze použít.
Popsaný algoritmus je ve skutečnosti algoritmem na maximální párování popsaný v kuchařce.
Výše popsaný způsob můžeme využít i na řešení zadané úlohy. Prostě jen nahradíme každý interval za seznam všech celých čísel v něm. Ovšem tímto postupem může vzniknou graf s až Θ(NV) hranami, což už je příliš.
Drobná optimalizace
Dá se všimnout, že když do jedné pozice padne alespoň N rezistorů, tak ať umístíme do ostatních pozic cokoliv, nějaký z možných rezistorů nám zbude. Tedy můžeme nejprve vyřešit úlohy bez pozic s hodně možnostmi a ty začít umisťovat až poté. Do grafu nebudeme dávat vrcholy rezistorů, do kterých by nevedla žádná hrana.
Tím se nám velikost grafu omezí na O(N2) vrcholů i hran. To už je algoritmus, jehož složitost závisí pouze na délce vstupu.
Laskavý čtenář nechť si rozmyslí implementační detaily stavění sítě a hledání nevyužitých odporů pro pozice s hodně možnostmi. Slibujeme, že to lze udělat v čase O(M log M). Na hledání nevyužitých odporů stačí jedno setřídění a pak chytřejší průchod.
Rychlejší řešení
Vzhledem k tomu, že v úloze se pracuje s intervaly, je na čase použít intervalové stromy. Tentokrát je ovšem nevyužijeme jako datovou strukturu, ale jejich princip využijeme při konstrukci sítě, na kterou pak spustíme algoritmus na toky. Postavíme si intervalový strom nad možnými odpory. Kořen bude stok a z ostatních vrcholů povede do otce hrana s hodnotou odpovídající délce intervalu, který vrchol reprezentuje.
Na tento strom dále připojíme vrcholy pozic na odpory. Připojování bude analogické operaci sečtení intervalu. Při sčítání vybereme vrcholy stromu tak, aby dohromady pokryly celý interval. My tedy připojíme jednotkové hrany tak, aby každá pozice byla pro každý interval připojená na ty vrcholy, které bychom chtěli sečíst.
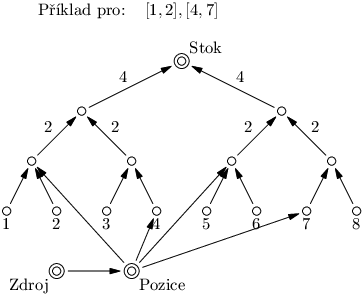
V takovém grafu najdeme maximální tok. Jak ale přečíst výsledné řešení? Začneme od listů intervalového stromu. Když tok teče do nějakého listu, tak daný odpor přiřadíme pozici, odkud tok teče. Dále budeme vyřizovat vyšší a vyšší úrovně stromu. Pro každou jednotku toku z vrcholů pozic se pokusíme najít volný rezistor v podstromu. Celý podstrom je totiž pro danou pozici možné využít. Navíc máme zaručeno, že v podstromu bude dostatek nevyužitých odporů, protože jediná hrana vedoucí z podstromu má kapacitu stejnou jako počet odporů v podstromu.
Pro nalezení nevyužitého odporu můžeme využít intervalového stromu. V každém vrcholu si budeme pamatovat počet ještě nevyužitých odporů a vždy půjdeme do podstromu, kde ještě nějaký je.
Stejně jako v naivním řešení zvládneme konstrukci udělat i v opačném směru, takže pokud tok není dostatečně velký, řešení neexistuje.
Alternativně si můžeme všimnout, že už to, že nám tok ukázal, z kterého intervalu máme do každé pozice přiřadit odpor, je dostatečné zjednodušení úlohy. Když totiž do každé pozice patří jen jeden interval, můžeme využít hladové řešení.
Výše popsaným řešením získáme graf s O(N+V) vrcholy, ovšem jen s O(M log V+V) hranami.
Optimalizace na závěr
Nechť [a, b] je nějaký interval hodnot odporů, uvnitř něhož nezačíná ani nekončí žádný ze zadaných intervalů. Pak listy intervaláče odpovídající rezistorům a, a+1,…, b můžeme nahradit za jeden list odpovídající celému intervalu. Hrana z tohoto vrcholu pak bude mít kapacitu b-a+1 a následující hrany v intervalovém stromě také budou příslušně zvětšené.
Takto můžeme zkomprimovat všechny intervaly, kde nic nezačíná ani nekončí, a postavit intervalový strom až na nich.
Jaké všechny intervaly to jsou můžeme zjistit tak, že si setřídíme všechny začátky a konce. Tyto hodnoty pak projdeme a spojíme úseky, kde nic není. Ke každé hodnotě si rovnou můžeme psát, do kolikátého z nových listů patří.
Touto modifikací se zmenší počet listů intervaláče na O(M). Tedy dostaneme graf s O(M) vrcholy a O(M log M) hranami. Až na nalezení toku mají zbylé části algoritmu časovou složitost O(M log M) a paměťovou O(M).
 35-3-S Vektorové prostory (Zadání)
35-3-S Vektorové prostory (Zadání)
Úkol 1 – Matice přechodu [7b]
Připomeňme si báze B a C. Vektory báze C roznásobíme a zapíšeme po mocninách, bude se nám to hodit.
|
|
Matici přechodu B[id]C sestavíme přesně podle návodu, do jejích sloupců přijdou vektory báze C zapsané v bázi B. Dokonce není třeba řešit soustavu rovnic, díky jednoduchosti báze B stačí opsat koeficienty u jednotlivých mocnin.
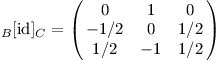
Ani při sestavování matice C[id]B nemusíme řešit soustavu rovnic. Báze C odpovídá funkčním hodnotám v bodech -1, 0, 1, v nich tedy vyhodnotíme polynomy báze B.
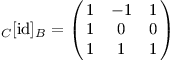
Ještě bylo možné využít jiný trik. Převod tam a zpět jsou inverzní operace, obdobně tedy matice přechodu jsou k sobě inverzní.
Se znalostí matic přechodu můžeme spočítat B[g]B:
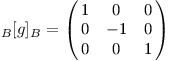
Jak šlo tuto matici nahlédnout geometricky? Zobrazení g zrcadlí podle osy y. Funkce 1 a x2 jsou symetrické (sudé), ty tedy měnit nemusíme. Funkce x je lichá, její obraz tvoří funkce -x.
Úkol 2 – Soustavy pomocí maticových prostorů [5b]
Sloupcový prostor odpovídá oboru hodnot zobrazení popsaném maticí A. Pokud b leží v oboru hodnot, tedy pokud b∈S(A), existuje alespoň jedno řešení x0.
Zbývá rozhodnout, jestli je řešení jednoznačné. To nám prozradí dimenze jádra. Pokud jádro totiž obsahuje nenulové xK, můžeme jej k x0 přičíst. Dříve platilo Ax0 = b, nově:
Nalezli jsme tedy nové řešení x0 + xK. Kdyby jádro obsahovalo pouze nulový vektor, tedy kdyby k = 0, tento postup by nefungoval a řešení by bylo jednoznačné.
Zároveň získáváme způsob, jak vyjádřit všechna řešení: Bude to množina x0 + xK pro všechny xK∈ker(A). Řečeno trochu jinak, množina všech řešení je afinní prostor vzniklý posunutím jádra ker(A) o x0. Tuto množinu parametricky zapíšeme snadno, každé řešení bude ve tvaru:
| k |
| i=1 |
Nechť má matice A rozměry n×n. Rozhodnout, jestli řešení existuje, umíme pomocí Gaussovy eliminace v O(n3). Vyjádření všech řešení parametricky trvá stejně dlouho.
Jakou časovou složitost má náš postup? Potřebujeme zjistit, jestli b∈S(A), tedy jestli existují vhodné koeficienty, aby platilo:
| r |
| i=1 |
Abychom dané koeficienty našli, musíme vyřešit soustavu rovnic. Zdánlivě jsme si nepomohli. Počet neznámých je ovšem pouze r, což může být méně než n, časová složitost se tak zlepší na O(r2 n). Kdybychom navíc znali ortonormální bázi, o které si povíme ve čtvrtém dílu, šlo by koeficienty najít v O(r n).
Známe-li x0, parametrický zápis dostaneme skoro zadarmo. Doplňme, že najít x0 by šlo opět v O(r n), konkrétně projekcí do R(A) – další lákadlo na čtvrtý díl.
Celý přístup má zjevný zádrhel, totiž že potřebuje znát báze maticových prostorů, pro rychlé řešení dokonce ve speciální podobě. Jejich nalezení by trvalo O(n3). Pokud bychom však s jednou maticí řešili více soustav (pro různá b), stačilo by báze najít jednou.
Úkol 3 – Rekurence [3b]
Hledáme koeficienty lineární kombinace a1, a2, které splňují následující rovnice:
| 0 = s0 | = a1 30 + a2 (-1)0 |
| 1 = s1 | = a1 31 + a2 (-1)1 |
Vychází řešení a1 = 1/4, a2 = -1/4, tedy:
| 1 |
| 4 |
| 1 |
| 4 |
Můžeme ověřit, že tento vzorec platí i pro další členy.