Druhá série třicátého pátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

• 35-2-1: Kde je Dan?
• 35-2-2: Zápisky z přednášky
• 35-2-3: Hroší šanta
• 35-2-4: Kamínky
• 35-2-S: Lineární zobrazení
• 35-2-X1: Oblázky

---

35-2-1 Kde je Dan? (Zadání)

---

Ještě než se pustíme do popisu řešení, pojďme si ujasnit několik věcí. Během popisu řešení budeme často mluvit o nějaké skupině lidí, co stojí vedle sebe (např. těch K lidí, které Dan vidí). Tuto skupinu lidí popíšeme pomocí intervalu pozic, na které stojí. Jelikož ale stojí v kroužku, tak rozlišujeme interval 3–6, což jsou pozice 3, 4, 5 a 6, a interval 6–3, což jsou pozice 6, 7, 8,…, N-1, N, 1, 2, 3. Délkou takového intervalu rozumíme počet pozic, které pokrývá.

Přímočaré řešení

Jistě bychom mohli úlohu vyřešit tak, že vyzkoušíme všechny Danovy pozice. Ke každé si spočítáme, v jakém intervalu musí být pozice člověka, aby ho Dan viděl. Potom se podíváme, kolik organizátorů je v tomto intervalu, a pokud jich je X, tak jsme našli další možnou pozici Dana.

Všimněme si ale, že každé Danově pozici odpovídá jiný interval pozic délky K a taky že každému intervalu délky K odpovídá jedna Danova pozice. Nemusíme tedy procházet Danovy pozice, ale jenom možné intervaly délky K.

Spočítání počtu organizátorů v daném intervalu zvládneme jedním průchodem seznamu organizátorů, který má velikost M. Možných umístění intervalu je N. Takže výsledná složitost je O(NM).

To je hodně pomalé

Nešlo by to rychleji? Šlo. Vytvoříme si pole N jedniček a nul. Číslo na pozici N je jedna, pokud na pozici N stojí organizátor, jinak je nula. Pomocí tohoto pole můžeme počet organizátorů v určitém intervalu vyjádřit pomocí součtu čísel na odpovídajích pozicích. Takovéto pole si vytvoříme v čase O(N), všude dáme nuly, a pak projdeme seznam organizátorů a na odpovídající místa v poli zapíšeme jedničku, což trvá čas O(M). Celkový čas je ale O(N), jelikož M ≤ N.

Zatím se zdá, že jsme si moc nepomohli. Když si vezmeme intervaly začínající na pozicích i a i+1, jejich velká část se překrývá (resp. překrývají se na K-1 pozicích). Tohoto překrývání můžeme využít pro rychlý přepočet součtu – odečteme číslo, které bylo ve starém intervalu, ale ne v novém, a přičteme to, které je v novém, ale nebylo ve starém.

Bereme-li tedy postupně intervaly 1–K, 2–K+1 atd., můžeme vždy v konstantním čase přepočítat počet organizátorů v aktuálním intervalu. To vede k času O(N).

Dodáváme, že počítat součet daného intervalu v nějakém poli jde v konstantním čase i pomocí prefixových součtů.

Ale N může být velké

V pozdější vstupech bylo N ≈ 10¹⁵, což je pro předchozí řešení příliš velké. Nedalo by se s tím něco dělat?

Jelikož M je relativně malé, všimneme si, že organizátoři musí stát daleko od sebe. Respektive existují dlouhé intervaly, kde nestojí žádný organizátor. Tyto intervaly bychom mohli šikovně přeskakovat a tím si ušetřit čas. Organizátory si nejprve setřídíme podle jejich pozice. Na začátku umístíme zkoumaný interval tak, aby začínal těsně za pozicí prvního organizátora, a spočítáme, kolik je v něm organizátorů. Budeme si pamatovat, který organizátor je první v intervalu a který je první těsně za aktuálnim intervalem. Nyní se podíváme, co se stane, když intervalem budeme posouvat – přibyde dřív nový organizátor do intervalu, nebo z něj dřív nějaký vypadne? Na tuto pozici přeskočíme a upravíme aktuální počet organizátorů. Pokud během tohoto skoku byl počet organizátorů X, tak každá přeskočená pozice (i ta, ze které jsme skákali) je pozice, která splňuje zadání a musíme je tedy všechny započítat. Když se pozice intervalu vrátí na startovní pozici, tak skončíme.

Jak jsme zlepšili čas? No, na setřídění pozic organizátorů potřebujeme čas O(M log M) a na následné posouvání intervalu potřebujeme čas O(M), jelikož každý organizátor právě jednou do intervalu vstoupí a právě jednou ho opustí. Výsledný čas je tedy O(M log M).

Program (Python)

Program (C++)

---

35-2-2 Zápisky z přednášky (Zadání)

---

Když už máme v ruce haldu, tak proč ji rovnou nepoužít? Provedeme v této haldě K-krát operaci extract_min a vypíšeme K-tý odebraný prvek. Operace extract_min má časovou složitost O(log N), tedy celkem O(K log N)

Nebudeme uklízet

Vzhledem k tomu, že je K výrazně menší než N, rádi bychom se zbavili závislosti na N. Na to si všimněme, že K-tý nejmenší prvek určitě bude nejhlouběji v K-té hladině. (Jinak by bylo nad ním alespoň K menších prvků, a potom by nebyl K-tý nejmenší.)

Proto si můžeme představit, že halda obsahuje pouze těchto K vrstev. Při operaci extract_min zastavíme probublávání ve chvíli, kdy se dostaneme do K té hladiny. Hlouběji náš hledaný prvek již nebude, tudíž tam už můžeme nechat naši haldu rozbitou.

A jakou toto má časovou složitost? Uděláme K operací extract_min a každá z nich projde K hladin, tedy celková složitost bude O(K²).

Když jedna halda nestačí…

Podívejeme se na naši situaci jinak. Uvažujme, že máme množinu L nejmenších prvků v naší haldě. Pokud bychom chtěli tuto množinu rozšířit, tak nám do množiny stačí přidat nejmenší prvek mimo ní. Ovšem prvek nad přidávaným vrcholem musí být menší než on, tedy musí být menší než nejmenší prvek mimo L. Přidaný vrchol tedy musí být synem nějakého vrcholu z L.

Opakovaným procházením všech synů a postupným přidáváním se dostaneme na složitost O(K²), ale všimněme si, že množina synů se mění jen málo – konkrétně jeden prvek odebereme a dva prvky přidáme. Tedy můžeme si naše prvky udržovat v nějaké šikovné datové struktuře – třeba haldě.

Pojďme si tedy pořídit (mini)haldu, ve které si budeme udržovat aktuální syny. Na začátku do minihaldy dáme kořen původní haldy. Poté K-1-krát budeme opakovat:

• Odstraníme nejmenší prvek z minihaldy.
• Přidáme jeho dva syny v původní haldě do minihaldy.

A na závěr vypíšeme nejmenší prvek z minihaldy.

A jakou toto bude mít složitost? Odstranění z minihaldy bude trvat O(log M), kde M je velikost minihaldy. Přidání synů bude též trvat O(log M). Ale jaká je velikost minihaldy? V každé z K-1 iterací přidáme 2 prvky, tedy v minihaldě bude nejvýše O(K) prvků. A odstranění a přidání provedeme O(K)-krát, tedy výsledná složitost bude O(K log K)

---

35-2-3 Hroší šanta (Zadání)

---

Grafy, grafy, všude grafy

Jak nám nadpis napovídá, můžeme problém převést na graf. Vrcholy budou dvojice objem vody v první nádobě a objem vody v druhé nádobě. Ty budeme značit (a, b). Hrany budou odpovídat jednotlivým akcím (nalití, vylití, přelití).

Nyní nám stačí najít nejkratší cestu z vrcholu (0, 0) do kteréhokoliv z vrcholů (K, b) nebo (a, K), kde a, b můžou být libovolné. A hledání můžeme provést prohledáváním do šířky, pro jehož oživení můžete nahlédnout do kuchařky o grafech.

Program (Python)

Pár důkazů

Předchozí algortitmus má časovou složitost O(AB). Nešlo by použít nějaký menší graf?

Podívejme se, jak se mění objemy vody ve džbánech. Pojďme si vzít například dva džbány s kapacitami 4 a 11:

Zdá se, že vždy je alespoň jeden džbán plný nebo prázdný. Pojďme si to dokázat.

Lemma o plnoprázdnosti: Vždy bude alespoň jeden ze džbánů plný nebo prázdný.

V začátečním stavu (0, 0) to zřejmě platí. A poté pro jednotlivé operace:

• Po naplnění bude alespoň tento džbán plný.
• Po vylití bude alespoň tento džbán prázdný.
• Přelití skončí tak, že vyprázdníme jeden džbán nebo naplníme druhý. Tak či tak bude na konci jedna z podmínek splněna.

Tedy náš algoritmus může uvažovat pouze stavy, kde jedna z nádob je plná nebo prázdná. Takových stavů je O(A+B).

Pojďme naše řešení ještě vylepšit. Všimněme si, že celkový objem vody v obou nádobách můžeme napsat vyjádřit jako:

kde c₁, c₂ ∈ Z. Proč to platí? Když přeleváme, zřejmě se stav vody nemění. Když plníme prázdný nebo vyléváme plný džbán, tak měníme příslušné c o 1. Pokud plníme nebo vyléváme z části naplněný džbán, tak druhý je plný nebo prázdný, a potom nový stav určitě půjde zapsat v tomto tvaru.

Můžeme si všimnout, že předchozí součet je určitě násobek gcd(A, B), takže nebude možné dosáhnout objemu, který není dělitelný největším společným dělitelem. A zase z lemmatu o plnoprázdnosti, jeden ze džbánů musí být plný, takže stavů bude nejvýše O((A + B) / gcd(A, B))

Možností je málo

Ukážeme, že předchozí postup je zbytečně složitý. Stačí všimnout, že většinou je další akce jasně daná, protože ostatní akce by nám byly k ničemu.

Stav, kdy je první džbán plný nebo prázdný a druhý džbán je plný nebo prázdný nazvěme triviální stav. Do triviálních stavů se z počáteční pozice zvládneme dostat pomocí nejvýše dvou operací, nedává tedt smysl se tam vracet později.

Pojďme provést rozbor případů podle toho, jakou akci jsme právě provedli. Bez újmy na obecnosti první džbán je plný nebo prázdný, což můžeme předpokládat díky lemmatu o plnoprázdnosti a tomu, že na pořadí džbánů nezáleží.

• Poslední akce byla vylití džbánu (a). Potom stav je (0, b) a akce bB nás dostanou do triviálního stavu, akce >a nic nedělají a na akci A jsme nemuseli džbán A vylívat. Jediná rozumná akce je tedy <.
• Poslední akce byla naplnění džbánu (A). Potom stav je (A, b) a akce bB nás dostanou do triviálního stavu, akce <A nic nedělají a na akci a jsme nemuseli A plnit. Jediná rozumná akce je tedy >.
• Poslední akce byla přelití džbánu (>). Stav může být jedna ze dvou možností:
  • (a, B): aA vedou do triviálního stavu, >B nic nedělají, pro < nebylo nutné předchozí >. Jediná rozumná akce je tedy b.
  • (0, b): bB vedou do triviálního stavu, >a nic nedělají, pro < nebylo nutné předchozí >. Jediná rozumná akce je tedy A.

A na začátku máme dvě možnosti, co dělat: Nalít první nebo druhý džbán. Dále je zbytek akcí daný. Stačí nám procházet obě větve najednou, a neprojdeme určitě více než je velikost výstupu, takže dosáhneme optimální složitosti, totiž lineární s velikostí výstupu O(V).

Program (Python)

Drobnost na závěr

Podívejme se ještě jednou na celkový objem vody ve džbánech a položme jej rovný K (za podmínky, že se K do jednoho džbánu vleze):

Tohle je ve skutečnosti Bézoutova identita, která je řešitelná Rozšířeným Eukleidovým algoritmem. (Co není v kuchařkách?)

Z Bézoutových koeficientů můžeme vyrobit přesný návod, jak dosáhnout výsledného postupu. Kladný koeficient říká, kolikrát máme daný džbán naplnit (z kohoutku, ne z druhého džbánu). Záporný koeficient říká, kolikrát máme daný džbán vylít (do dřezu).

Nejjednodušší je případ, kdy c = 0, tedy K je násobkem objemu jednoho ze džbánů. Poté nám stačí daný džbán plnit a přelévat do druhého.

V opačném případě jeden z koeficientů bude záporný. (Jinak by rovnice zřejmě neplatila, protože jeden ze džbánů má větší objem než K.) Potom stačí plnit džbán s kladným koeficientem a vždy přelít do druhého džbánu, dokud nebude plný. Potom, co ho bude plný, ho vylejeme, nalejeme do něj zbytek z prvního džbánu a začneme znova, dokud nedosáhneme kýženého výsledku.

Potom nám stačí najít takové dva koeficienty, které nám dají nejmenší počet akcí. Jsou dvě možnosti, totiž nejmenší kladné a největší záporné c₁ a k nim jejich odpovídající c₂. Celkový počet akcí potom bude 2(c₁ + c₂). Stačí obě možnosti porovnat a výslednou posloupnost akcí vygenerovat. Mimochodem to znamená, že počet akcí umíme najít v čase O(log(min(A, B))).

---

35-2-4 Kamínky (Zadání)

---

Přímočarý přístup

Přímočaré řešení spočívá v tom, že budeme řadu kamínků opakovaně procházet a odstraňovat sousední stejnobarevné kamínky. Složitost tohoto přístupu je však O(N²).

Pokud má úloha řešení, určitě má i řešení s maximálním počtem hladových odebrání, tedy takových, která vyřadí první stejnobarevnou dvojici. Představme si tedy, že existuje řešení, které přeskočilo nějakou stejnobarevnou dvojici. Zaměřme se na tu nejlevější dvojici takto neodebraných kamínků k₁ a k₂. Pokud se jedná o platné řešení, znamená to, že k₁ se v řešení odebírá společně s nějakým q₁ a k₂ společně s nějakým q₂. Můžeme nahlédnout, že lze tyto čtyři kamínky eliminovat v jiném uspořádání, to jest k₁ spolu s k₂ a q₁ spolu s q₂, čímž jsme dosáhli řešení, které dělá více hladových odebrání.

Tak jsme tedy dokázali, že řešení s maximálním počtem hladových odebrání je to řešení, které dělá hladové odebrání vždy.

Řešení s použitím zásobníku

Vytvoříme si zásobník a budeme do něj postupně ukládat navštívené barvy. V případě, že bychom měli do zásobníku přidat kamínek barvy b a v zásobníku byl současný vrchní kamínek také barvy b, prostě je oba odstraníme.

Takto projedeme celou posloupnost a pokud v zásobníku na konci něco zbylo, má pravdu Světlana a není možné vyhrát. Pokud je však zásobník na konci prázdný, znamená to, že Khebir vyhrát může.

Protože jsme pro každý prvek posloupnosti vykonali řádově O(1) operací, má celý algoritmus složitost O(N).

Proč algoritmus funguje?

V zásobníku máme vždy uloženy kamínky tak, že zde nejsou dva kamínky stejné barvy vedle sebe. Na začátku zásobník tuto podmínku splňuje a vždy, když přidáme nový kamínek, tak odstraníme poslední dvojici, pokud jsou to dva stejné vedle sebe (a na zbytku zásobníku už různobarevnost sousedů předpokládáme). Tudíž se tato vlastnost zachovává.

Když projdeme celou posloupnost a takto jí vložíme do zásobníku, máme na konci zajištěné, že v zásobníku je posloupnost, ve které nejsou dvě stejné barvy vedle sebe, a do zásobníku byly přidány všechny kamínky. Pokud je tedy na konci délka zásobníku nenulová, znamená to, že už žádnou další eliminaci provést nelze a tudíž nelze vyhrát, naopak pokud je zásobník na konci prázdný, znamená to, že všechny kamínky vyřadit lze.

---

35-2-X1 Oblázky (Zadání)

---

Začneme jednoduchým pozorováním: Když máme posloupnost sousedních kamínků stejné barvy delší než jedna, tak se jí umíme zbavit. Existuje spousta možností jak na to. Například sudé posloupnosti budeme odebírat po dvou a u lichých začneme odebráním trojice, pokud něco zbude, tak můžeme opakovat odebírání dvojic. Můžeme tedy povolit odebírat i více než dva nebo tři kamínky a hra se tím nijak nezmění.

Dále nahlédneme, že můžeme předpokládat o posledním kamínku, že bude odebrán jako poslední. Podívejme se na nějakou validní posloupnost tahů jak odebrat všechny kamínky. Poslední kamínek bude odebraný spolu s nějakými dalšími stejné barvy (těm budeme říkat kamarádi). Všechny kamínky mezi kamarády a posledním musely být odebrány ještě před posledním (jinak by nešlo provést uvažované odebrání). Po odebrání už tedy zbudou jen kamínky nalevo od prvního kamaráda. Libovolná následující operace tedy už může odstraňovat pouze kamínky z této části. Vůbec tedy nezáleží na tom, jestli tyto operace proběhnou před nebo po odebrání nejpravějšího kamínku. Můžeme tedy operaci odebírající poslední kamínek provést až úplně nakonec a stále máme validní způsob odebírání.

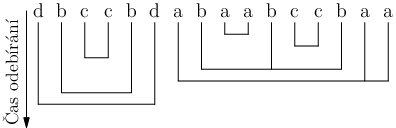
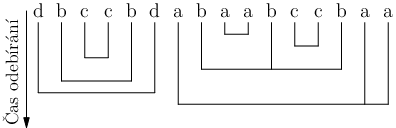
Nyní již k samotnému algoritmu: Využijeme dynamického programování. Pro každý souvislý úsek kamínků určíme, jestli jde nebo nejde odstranit. Prázdné úseky jsou vždy řešitelné, protože již není co odstraňovat. Při počítání nějakého úseku již budeme mít spočteny všechny jeho souvislé podúseky. To můžeme snadno zařídit tím, že budeme počítat od nejkratších úseků k delším. Zkusíme všechny možnosti, jak mohl vypadat poslední tah při odstraňování daného úseku. Tedy vyzkoušíme všechny dvojice nebo trojice kamínků stejné barvy obsahující poslední kamínek. Když alespoň jedna bude fungovat, tak máme vyhráno. Všechny ostatní kamínky úseku již musely být odstraněny. Ovšem kamínky odstraněné v posledním tahu tvoří jakousi bariéru: části úseku, které oddělují, spolu nemohly nijak interagovat, a tedy každá z částí (což je zase úsek) musela být odstraněna samostatně. Jestli bylo možné odstranit každou z částí zjistíme z již spočítaných hodnot dynamického programování.

Pokud je celá posloupnost řešitelná, tak snadno zvládneme zjistit výherní posloupnost tahů. U každého podúseku si zapamatujeme, jakým posledním tahem jsem naši řešení, a pak využijeme jednoduché rekurzivní funkce, která se nejprve zarekurzí na všechny úseky, které odděluje poslední tah, a pak vypíšeme i onen tah.

Jak to bude rychlé? Počítáme Θ(N²) souvislých podúseků. V každém ovšem zkoušíme spoustu možností posledního tahu. Pokud budeme počítat s původní hrou bez žádných pozorování, tak máme O(N³ + N²) možností posledního tahu a každou z nich je nutné ověřit. Celkem tedy algoritmus běží v O(N⁵). Když využijeme druhé pozorování, tak víme, že stačí zkoušet pouze poslední kamínek a jeden nebo dva z předešlých. Celkem tedy O(N⁴).

Nyní pojďme uvažovat nad hrou, kde je možno odebrat i větší celky než trojice (v úvodním pozorování jsme si uvědomili, že je to ekvivalentní). To na první pohled vypadá, že jsme si vůbec nepomohli, protože teď je třeba uvažovat až exponenciálně množností posledního tahu. Pojďme to napravit. Zvlášť uvážíme možnost, že poslední tah odebral dvojici. Takové tahy prostě vyzkoušíme v lineárním čase. Zbývají tedy už jen odstranění alespoň trojiček. Podívejme se na předposlední z odstraněných kamínků v posledním tahu (označme x). Všimneme si, že úsek od začátku po x (včetně) musí být také řešitelný. Můžeme odstranit všechny úseky oddělené posledním tahem stejným způsobem a pak jen použijeme stejný poslední tah bez posledního kamínku. Jelikož uvažujeme jen poslední tahy odstraňující alespoň tři kamínky, tak nám zůstane stále validní tah. Ovšem toto platí i opačně. Když máme nějaké x stejné barvy jako poslední kamínek a úseky od začátku po x (včetně) a od x (mimo) po poslední kamínek (mimo) jsou řešitelné, tak i to celé je řešitelné. Důkaz ponecháváme čtenáři jako cvičení. Stačí tedy jen vyzkoušet všechny stejně obarvené x a ověřit předešlou podmínku.

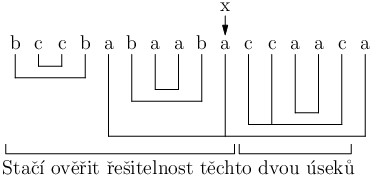
Celková časová složitost tohoto řešení je O(N³). Paměťová je O(N²).

---

35-2-S Lineární zobrazení (Zadání)

---

Úkol 1 – Nelineární zobrazení [2b]

Těchto zobrazení existuje mnoho. My si ukážeme dvě jednoduchá.

Pro první zobrazení si představme, že máme obrázek nakreslený na průhledné fólii. Tuto fólii přehneme podle vodorovné osy, čímž se spodní část obrázku zrcadlově převrátí. Takové zobrazení lze zapsat pomocí absolutní hodnoty:

Absolutní hodnota očividně není lineární funkce, ale přesto ověříme, že naše zobrazení není lineární. Dokážeme najít protipříklad jak pro součet:

Tak i pro násobek skalárem:

Druhé zobrazení je podobně přímočaré, obrázek o kus posuneme, konkrétně ve směru nějakého vektoru a.

Ač se posunutí může zdát jako přirozená transformace, definici linearity nesplňuje. Ověřme to pro a = (1, 1)^⊤:

Můžeme jednoduše nahlédnout, že dané zobrazení není lineární, kdykoli vektor a není nulový.

Úkol 2 – Fibonacciho čísla [5b]

Nejdříve potřebujeme vytvořit matici Q, která bude generovat postupně další Fibonacciho čísla. Tedy když uděláme součin matice Q a vektoru (F_n, F_n+1)^⊤, chceme získat vektor (F_n+1, F_n+2)^⊤ neboli

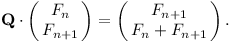
První řádek matice je jednoduchý, chceme okopírovat druhou složku vektoru do první složky. Hledáme tedy koeficienty, kterými vynásobit složky prvního vektoru:

Druhý řádek není o moc těžší, potřebujeme členy F_n, F_n+1 sečíst.

Výsledná matice Q bude vypadat následovně:

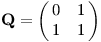
Můžeme provést rychou kontrolu, že máme vše správně:

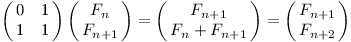
Nyní můžeme začít řešit, jak vypočítat F_n. Budeme začínat s F₀ a F₁, tedy s vektorem f₀ = (0, 1)^⊤. Víme, že matice Q nám vypočítá následující člen. Když výsledný vektor vynásobíme znovu maticí Q, tak dostaneme ještě další člen. Například F₃ bychom spočítali takto:

Technicky by nám stačilo o jedno násobení maticí Q méně a výsledek bychom přečetli z druhé složky vypočteného vektoru. Poté bychom však museli ošetřit speciální případ pro výpočet F₀.

Jelikož je násobení matic asociativní, můžeme výpočet zapsat bez závorek:

Což lze ještě více zjednodušit na Q³ ·f₀.

Náš obecný algoritmus tedy nejprve spočítá Qⁿ, posléze touto maticí vynásobí vektor f₀ a výsledek přečte z první složky.

V obecnosti násobení dvou čtvercových matic velikosti n podle definice trvá O(n³), ale jelikož my násobíme jen matice 2×2 a velikost těchto matic není závislá na velikosti problému, který řešíme, tak jedno násobení budeme brát jako konstantní, tedy O(1). Pro výpočet Qⁿ potřebujeme n násobení, celkem tedy náš algoritmus běží v čase O(n).

To je však pomalé. Vždyť totéž umíme jednoduše bez lineární algebry! Zbývá poslední dílek skládanky – jak rychle vypočítat mocninu matice Q.

Rychlé mocnění

Využijeme mocninový trik. Jistě ze střední školy znáte pravidlo sčítání mocnin:

Tuto vlastnost využijeme obráceně. Dejte tomu, že chceme vypočítat 3ⁿ, kde n je sudé. Pak stačí spočítat 3^n/2, protože poté již dopočítáme 3ⁿ = 3^n/2 ·3^n/2.

Kdyby bylo n liché, spočítáme 3^(n-1)/2. Díky tomu dopočítáme 3ⁿ = 3^{(n-1) / 2} ·3^{(n-1) / 2} ·3.

Spojením těchto dvou pravidel:

Zápis ⌊n/2⌋ značí podíl zaokrouhlený dolů. Pro sudé n dostaneme n/2, pro liché n zase (n-1)/2, přesně jako výše. Dále zápis n mod 2 značí zbytek po dělení dvěma.

Pokud známe mocninu 3^⌊n/2⌋, výsledek spočítáme na konstantně mnoho operací. Pokud danou mocninu neznáme, tak ji můžeme rekurzivně vypočítat. V každém rekurzivním volání se mocnina sníží na půlku, celkem tedy budeme potřebovat log₂ n volání. Tedy celkový čas rychlého mocnění bude O(log n).

Daný algoritmus jsme si ukazovali na číslu 3, pochopitelně však platí i pro matice, jen musíme provést maticové násobení. To v důsledku znamená, že n-té Fibonacciho číslo dokážeme vypočítat v čase O(log n).

Úkol 3 – Dosažitelnost [5b]

Umíme spočítat sledy délky ℓ z i do j. Pokud je tento počet pro nějaké ℓ nenulový, pak existuje cesta z i do j. První myšlenka tedy bude počítat A^ℓ pro různá ℓ, hledat nenulové hodnoty a na příslušná místa v matici dosažitelnosti psát jedničky. Pro n vrcholů nám stačí projít 0 ≤ ℓ< n, protože každá cesta bude mít nejvýše n-1 hran.

Počet sledů však může růst exponenciálně, chceme se vyhnout počítání s takto velkými čísly. Naštěstí nepotřebujeme znát počet sledů přesně, zajímá nás pouze to, jestli je tento počet nenulový. Po každém kroku tedy všechny nenulové hodnoty v A^ℓ změníme na jedničky.

Tento postup provede n násobení matic n ×n. Při použití násobení dle definice dostaneme časovou složitost O(n⁴).

Nešlo by to lépe? Použijeme-li rychlé mocnění, zvládneme Aⁿ spočítat jen na O(log n) násobení. Jenže to nám moc nepomůže, potřebujeme i všechny mocniny mezi tím. Z matice Aⁿ samotné totiž matici dosažitelnosti sestavit nedokážeme. Pokud například mezi vrcholy i,j existuje pouze jediný sled délky 1, bude (Aⁿ)_i,j = 0.

Jakmile je jednou pro nějaké ℓ počet sledů nenulový, chceme zařídit, aby už nenulový zůstal. Řešení je jednoduché, do grafu přidáme smyčky (hrany vedoucí zpět do téhož vrcholu). V matici sousednosti to znamená vyplnit diagonálu jedničkami.

S takto upravenou maticí A již můžeme použít rychlé mocnění. Přidáme nahrazování velkých čísel za jedničky a máme finální algoritmus. Jeho časová složitost bude O(n³ log n).

Jak je toto řešení vlastně rychlé? Srovnejme jej s přímočarým řešením, které z každého vrcholu spustí prohledávání do šířky. Jedno prohledání má složitost O(n + m), což by pro hustý graf s mnoho hranami bylo O(n²). Prohledání ze všech vrcholů by zabralo O(n³).

Zdá se, že naše sofistikované řešení je vlastně k ničemu. Stačí si však vzpomenout na Strassenův algoritmus, který naši složitost vylepší na O(n^2.807 log n), což už je lepší než přímočaré prohledávání. Nutno však podotknout, že pro praktické velikosti grafů je rozdíl minimální.

Úkol 4 – Obecná inverze [3b]

Inverzi by jistě šlo spočítat řešením soustav rovnic. Zde však nabídneme geometrický náhled.

Konstanta c pouze obrázek zvětšuje, z matice ji můžeme vytknout.

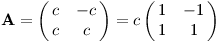
Zjistíme, že matice otáčí o 45^°. Navíc vektory ještě trochu protáhne, původní jednotkové vektory měly délku 1, nyní mají délku √1² + 1² = √2.

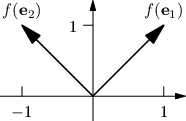
Sestavme tedy obdobnou matici pro otočení v opačném směru:

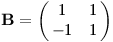
To už je skoro hledaná inverzní matice. Ještě musíme zajistit, aby měly vektory správnou velikost. Matice A zvětšovala c √2-krát, matice B zvětšuje √2-krát. Podělíme tedy členem 2c a máme inverzi.

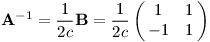
Pro c = 0 inverze existovat nemůže, protože taková matice A každý obrázek zmenší do jediného bodu.

Menu