První série třicátého pátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 35-1-1: Hroší přeslička
- 35-1-2: Vaření lektvarů
- 35-1-3: Letadélko
- 35-1-4: Atlas zlomků
- 35-1-S: Lineární rovnice
- 35-1-X1: Rejstřík zlomků
 35-1-1 Hroší přeslička (Zadání)
35-1-1 Hroší přeslička (Zadání)
Celou situaci převedeme do řeči teorie grafů. Horu si představíme jako graf, který je stromem. Křižovatky budou odpovídat vrcholům grafu, cestičky pak hranám mezi nimi. Vrchol hory odpovídá kořenu stromu.
Místo toho, abychom postupně zkoušeli všechny trasy a zjišťovali jejich nejvyšší bod, zamysleme se nad tím, kolikrát je daný vrchol nejvyšším bodem nějaké trasy.
Nejprve rozeberme situaci, kdy je uvažovaný vrchol kořenem. Nechť kořen r sousedí s Nr vrcholy, označme je v1 až vNr. Velikost podstromu začínajícího ve vi označme ci, do podstromu počítáme i vi samotný. Hodnota ci také odpovídá počtu všech vrcholů, ze kterých vede cesta do r přes vi.
Kolikrát je kořen nejvyšším bodem nějaké trasy? Zcela jistě, pokud nějaká trasa vede přes kořen, pak je kořen jejím nejvyšším vrcholem. Zajímá nás tedy počet cest, které vedou přes kořen.
První možnost je, že trasa v kořenu končí. V takovém případě začíná v podstromu jednoho ze synů kořene v1, …, vNr. Počet všech vrcholů v nich zjistíme sečtením velikostí těchto podstromů:
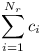
Stejný počet dostaneme, pokud nám trasa začíná v kořenu a končí v jednom z vrcholů.
Jinak trasa v kořenu nekončí, ani nezačíná. Pak musí krajní vrcholy trasy spadat do různých podstromů. Kdyby totiž spadaly do stejného podstromu pod vi a kořen by ležel na trase, znamenalo by to, že hrana vedoucí z kořenu do vi by byla na trase dvakrát, což ze zadání není možné. Stejně tak platí, že pokud leží koncové vrcholy v různých podstromech, pak kořen na trase být musí. Trasa vede mezi různými podstromy a mezi nimi může trasa vést pouze přes kořen.
Takových tras je:
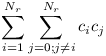
Počáteční vrchol můžeme vybrat z libovolného podstromu, k němu koncový pouze z podstromů nějakého jiného syna.
| Nr |
| i=1 |
| Nr |
| i=1 |
| 2 |
| i |
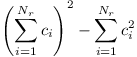
Celkově tak umíme z velikostí podstromů synů spočítat, kolikrát se kořen vyskytne jako nejvyšší vrchol nějaké trasy:
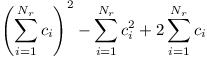
Nyní se zamysleme, jak by se situace změnila pro vrchol u, který není kořenem. Kromě případů, které jsme již rozebrali, se nyní mohlo stát, že alespoň jeden z krajních vrcholů trasy není v podstromu u. Pak ale u nemůže být nejvyšším vrcholem trasy – jeho otec musí být rovněž na trase.
Zajímají nás tedy pouze takové dvojice, kde oba vrcholy leží v podstromu u. Nyní jako vi označíme podstromy synů u. Zbytek výpočtu bude stejný jako pro kořen.
Umíme tedy pro každý vrchol ve stromu spočítat, kolikrát je nejvyšším bodem trasy. Jak to spočítat efektivně pro celý strom?
Můžeme to udělat upraveným prohledáváním do hloubky – před návratem z rekurze vrátíme velikost daného podstromu. Tu spočítáme snadno jako součet velikostí podstromů synů plus jedna. Stejně tak před tím, než se vrátíme, můžeme spočítat, kolikrát daný vrchol bude nejvyšším na trase, a případně upravit udržované globální maximum (a v jakém vrcholu to maximum je).
Jaká je časová složitost takového algoritmu?
V každém vrcholu trávíme čas lineární vzhledem k počtu synů. Jenže celkový počet synů přes všechny vrcholy nemůže být větší, než kolik je vrcholů, tedy celková složitost je lineární.
Jelikož si pamatujeme strukturu celého grafu, je i paměťová složitost lineární.
 35-1-2 Vaření lektvarů (Zadání)
35-1-2 Vaření lektvarů (Zadání)
Nejprve proveďme následující pozorování – pokud chce Demivirtos začít vařit nějaký lektvar v nějakém čase, ale mohl by jej začít dříve, pak si určitě nepohorší, když jej začne vařit dříve. Následující lektvar by totiž mohl nechat vařit ve stejný čas, anebo dříve a tak dále až do posledního lektvaru, čímž by dovaření posledního lektvaru mohl pouze uspíšit. To ale znamená, že se mu vyplatí každý lektvar uvařit, co nejdříve to lze, tedy hned, jakmile se dovařily jeho prerekvizity.
Zbývá tedy pro každý lektvar zjistit, kdy se dokončí, pokud všechny lektvary dáme vařit hned, jak to půjde. Na to použijme následující algoritmus – upravené hledání topologického uspořádání.
V průběhu si udržujme množinu všech lektvarů, které nemají žádné nehotové prerekvizity. Její stav na začátku můžeme zjistit tak, že projdeme všechny prerekvizity a následně si poznamenáme ty lektvary, které nemají žádnou prerekvizitu. U těch zbylých si poznamenáme, kolik prerekvizit mají.
Nyní vždy vezmeme jeden lektvar, který nemá žádnou prerekvizitu – máme zaručeno, že takový existuje, jinak by na sebe dva nebo více lektvarů navzájem čekalo. Dáme jej vařit v čase, kdy dovařila nejpozdější z jeho prerekvizit – to si budeme ukládat a průběžně aktualizovat u každého lektvaru – a poznamenáme si, že skončí v čase, kdy začal, plus doba jeho vaření. Nyní u každého lektvaru, jehož prerekvizitou daný lektvar je (to si pamatujeme u daného lektvaru), snížíme počet zbývajících prerekvizit o jedna a případně upravíme, kdy se dovaří nejpozdější prerekvizita.
Zbývá aktualizovat množinu lektvarů, které již nemají neuvařené prerekvizity. Jenže to mohou být pouze ty, které měly jako prerekvizitu lektvar, který se právě uvařil, jinak bychom je přidali již předtím. Stačí tedy pouze u těchto zkontrolovat, zda jsou splněné jejich prerekvizity (to poznáme tak, že počet zbývající prerekvizit je nula). Pokud ano, pak je přidáme mezi lektvary, které lze hned uvařit.
Jakmile dovaříme všechny lektvary, stačí je znovu projít a najít ten, který se dovaří nejpozději.
A jakou to má složitost?
Na začátku jen procházíme všechny lektvary a prerekvizitové vztahy, na konci všechny vrcholy – to obojí má lineární velikost vzhledem k počtu lektvarů plus celkovému počtu prerekvizit. Zbývá analyzovat prostřední část – jenže tam na každý lektvar sáhneme pouze jednou a aktualizace lektvarů, kterým je prerekvizitou, můžeme naúčtovat prerekvizitovému vztahu, na který sáhneme také pouze jednou. Tedy i tato část má lineární časovou složitost vzhledem k délce vstupu.
V paměti máme uložené všechny lektvary a všechny prerekvizity, tedy i prostorová složitost je lineární.
 35-1-3 Letadélko (Zadání)
35-1-3 Letadélko (Zadání)
Protože počet otazníků byl ze zadání velmi malý, označme si ho K a počítejme časovou složitost i vzhledem k němu.
První, co nás napadne, je vyzkoušet všechny možnosti, jak mohlo letadlo letět. Všech možností je 2K, a když každou doplníme a zkontrolujeme, dostaneme počet validních možností. Tento algoritmus bude ale ukrutně pomalý: O(N ·2K)
Zlepšujeme
Teď tedy budeme muset přijít na něco lepšího – všimněme si, že pokud letadlo měnilo několikrát výšku, nezáleží, jak přesně tyto výšky měnilo, ale stačí jen vědět, v jaké výšce skončilo (za předpokladu, že se neutopilo).
Z toho můžeme všechny lety, které skončí ve stejné výšce, seskupit a chovat se k nim stejně.
Označme si d[i][h] počet letů, které po i změnách výšek skončí ve výšce h.
Pojďme si najít zřejmé hodnoty. Letadlo začíná ve výšce 0: d[0][0] = 1, a pokud výška nulová není: d[0][h] = 0. A nikdy nesmí klesnout pod hladinu: d[i][-h] = 0.
Nyní nám jen zbývá vymyslet, jak vypočítat d[i+1] z d[i]. Pokud jsme v letu stoupli, tak všechny lety zvýšily výšku o 1: d[i+1][h] = d[i][h-1], pokud jsme naopak klesli: d[i+1][h] = d[i][h+1]. A zbývá nám vyřešit poslední případ, kdy nevíme, co se stalo. Pak se mohlo stát obojí: d[i+1][h] = d[i][h-1] + d[i][h+1].
Potom, co toto všechno spočítáme, chceme, aby letadlo skončilo v nulové výšce, tedy odpověď je d[N][0].
A jakou má toto složitost? Máme N sloupců, letadlo může za let vystoupat až do výšky N a výpočty jednotlivých polí provedeme v konstantním čase. Celkem O(N2).
Zlepšujeme ještě jednou
Všimněme si ale, že rozptyl výšek, ve kterých se letadlo může v jeden časový okamžik nacházet, je velmi malý, totiž 2K. Většina tabulky tak bude zaplněná nulami. Když si budeme udržovat okénko velikosti 2K, tak nám to zredukuje časovou složitost na O(NK).
A ještě jednou
Nicméně naše řešení můžeme ještě zlepšit. Pokud totiž na naší pozici není otazník, tak se celý sloupec pouze posune o 1 nahoru nebo dolů, a tedy ho můžeme zachovat (jen ořízneme utopená letadla – protože jsme klesli v aktuálním kroku jen o jedna, tak může být utopené letadlo jen jedno). Vypočítat nové okénko velikosti 2K potřebujeme pouze na každém otazníku, tedy K-krát. Tím zlepšíme časovou složitost na O(N+K2).
 35-1-4 Atlas zlomků (Zadání)
35-1-4 Atlas zlomků (Zadání)
Máme najít všechny zlomky a/b ∈<0,1>, které jsou v základním tvaru a 1≤ b≤ N. Zlomek 0/1 vypíšeme zvlášť, pak už se můžeme spolehnout na to, že čitatel je nenulový. Postačí tedy najít všechny uspořádané dvojice (a,b) takové, že 1≤ a≤ b≤ N a čísla a a b jsou nesoudělná (to znamená, že jejich největší společný dělitel je 1).
Dřevorubecké řešení
Můžeme si vzít všechny dvojice (a,b) s 1≤ a≤ b≤ N, pro každou z nich spočítat největšího společného dělitele (NSD), a pokud vyjde 1, dvojici vypsat.
Jak počítat NSD? K tomu se hodí Euklidův algoritmus. Zde ho popíšeme jen stručně, detaily najdete v kuchařce o teorii čísel. Jednodušší verze algoritmu opakovaně od většího čísla odečítá menší, a až se vyrovnají, prohlásí výsledek za NSD. Výpočet se určitě zastaví, protože každým krokem se zmenší součet a+b aspoň o 1. Výsledek je správně, neboť každý krok zachovává množinu všech společných dělitelů, a tedy i NSD.
Algoritmus může potřebovat až a+b kroků, což v našem případě je O(N). To je hodně, ale lze to jednoduše zrychlit. Pokud by třeba bylo a=999 a b=7, opakovaným odčítáním b od a nakonec spočítáme 999 mod 7 = 5. Místo odčítání tedy můžeme větší číslo rovnou vymodulit menším. Jen pozor na to, že takto uděláme o krok navíc, takže algoritmus se nezastaví s a=b, nýbrž až s a=0 – tehdy je NSD rovno b.
V kuchařce dokazujeme, že modulící verze Euklidova algoritmu provede O(log(a+b)) průchodů. Tím pádem naše řešení vyzkouší O(N2) dvojic (a,b), pro každou z nich v čase O(log(2N)) = O(log N) spočítá NSD a případně dvojici vypíše. Celková časová složitost tedy činí O(N2 log N).
Kešování mezivýsledků
Předchozí řešení počítá NSD mnoha dvojic. Přitom určitě mnohokrát dojde ke stejnému mezivýsledku. Pomůžeme si tedy myšlenkou z dynamického programování a budeme si ve dvojrozměrném poli D pamatovat, pro které dvojice jsme už NSD spočítali, a nebudeme je počítat znovu. Jelikož se všechny mezivýsledky pohybují mezi 0 a N, bude pole D zabírat prostor O(N2).
Postačí nám odčítací verze Euklidova algoritmu. Zapíšeme ji rekurzivně:
nsd(a, b)
- Pokud D[a,b]=0: ◁ nsd(a, b) ještě neznáme
- Pokud a=b: D[a,b]=a.
- Pokud a>b: D[a,b] = nsd(a-b, b).
- Pokud a<b: D[a,b] = nsd(a, b-a).
- Vrátíme D[a,b].
Představme si, že jsme tuto funkci postupně zavolali pro K různých dvojic. Ona sama se nejspíš rekurzivně zavolala pro spoustu dalších dvojic. Ale pouze v O(N2) případech se může stát, že políčko D[a,b] ještě není vyplněné, takže rekurze bude pokračovat. V ostatních případech se hned vrátíme – tento čas můžeme naúčtovat tomu, kdo nás zavolal, což je buďto vyplňování políčka, nebo jedno z K původních volání „zvenku“.
Celkem tedy výpočty NSD strávíme čas O(N2 + K). V naší úloze je ovšem K také O(N2), takže celý algoritmus doběhne v čase O(N2).
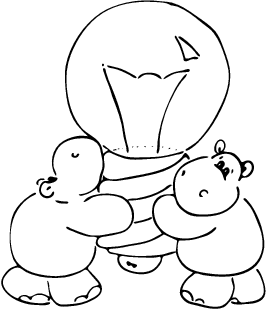
Euklidův algoritmus pozpátku
Úloha po nás chce optimalizovat časovou složitost vzhledem k počtu vypsaných zlomků – budeme mu říkat třeba Z. Jak dobré je v tomto ohledu předchozí řešení? To záleží na tom, jak velké je Z vzhledem k N2. Pokud je výrazně menší, trávíme spoustu času dvojicemi (a,b), které se nakonec ukáží být soudělné, takže je zahodíme. Tak raději vymyslíme, jak se soudělným dvojicím rovnou vyhnout.
Výpočet NSD pro každou nesoudělnou dvojici skončí ve dvojici (1,1). Co kdybychom zkusili provádět Euklidův algoritmus pozpátku a kdykoliv bychom drželi v ruce nějakou dvojici (a,b), prozkoumali bychom všechny možnosti, odkud se do ní algoritmus mohl dostat. To jsou jenom dvojice (a+b,b) a (a,a+b).
Budeme pokračovat rekurzivně. Jakmile a nebo b překročí N, rekurzi zastavíme – všechny další dvojice v této větvi výpočtu by byly ještě větší. Ještě si všimneme, že na každý zlomek narazíme právě jednou, protože Euklidův algoritmus má v každém kroku jednoznačně určený následující krok.
Jediný háček je v tom, že nevynucujeme a≤ b, takže vypsané zlomky mohou být větší než 1. Všimněte si, že tuto podmínku nelze vynucovat průběžně, jelikož ke dvojicím s a≤ b může být potřeba dojít přes dvojice s a>b. Naštěstí stačí zlomky větší než 1 prostě nevypisovat – jelikož tvoří nejvýše polovinu všech vygenerovaných zlomků, časovou složitost si tím nezhoršíme.
Program bude vypadat takto:
Zlomky(a, b)
- Pokud a>N nebo b>N, vrátíme se.
- Pokud a≤ b, vypíšeme zlomek a/b.
- Zavoláme Zlomky(a+b, b).
- Zavoláme Zlomky(a, a+b).
Výpočet odstartujeme zavoláním Zlomky(1,1).
Časovou složitost odhadneme snadno. Každé volání funkce, které prošlo přes podmínku v 1. kroku, vypíše jeden zlomek. Těmito voláními tedy strávíme čas O(Z). Ostatní volání se hned vrátí, takže je můžeme naúčtovat tomu, kdo je zavolal.
Tak jsme získali jednoduchý algoritmus s časovou složitostí O(Z), což je zjevně optimální.
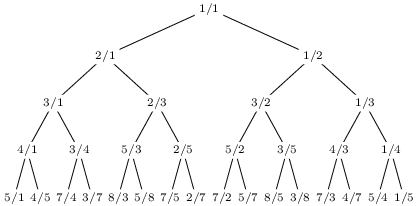
Calkinův-Wilfův strom
Mimochodem, všechna volání naší funkce Zlomky můžeme znázornit následujícím stromem. Říká se mu Calkinův-Wilfův strom, a jak jsme dokázali, obsahuje každý kladný zlomek právě jednou.
Trocha asymptotiky na závěr
Ještě jsme nezjistili, jaký je vztah mezi Z a N2, tedy jak daleko je kešovací algoritmus od optima. V této poněkud matematičtější sekci dokážeme, že Z≥ cN2 pro nějakou konstantu c>0. Takže N2 je ve skutečnosti O(Z) a kešovací algoritmus je (aspoň asymptoticky) optimální.
 Označme M množinu všech dvojic (a,b) takových, že 1≤ a,b≤ N.
Zjevně je |M|=N2. Dále buď S⊆ M podmnožina obsahující všechny
soudělné dvojice. Dokážeme, že |S|≤ dN2 pro nějakou konstantu 0<d<1.
Nesoudělných tedy bude alespoň (1-d)N2, z toho s a≤ b aspoň (1-d)/2·N2.
Označme M množinu všech dvojic (a,b) takových, že 1≤ a,b≤ N.
Zjevně je |M|=N2. Dále buď S⊆ M podmnožina obsahující všechny
soudělné dvojice. Dokážeme, že |S|≤ dN2 pro nějakou konstantu 0<d<1.
Nesoudělných tedy bude alespoň (1-d)N2, z toho s a≤ b aspoň (1-d)/2·N2.
Pro libovolné prvočíslo 2≤ p≤ N označíme Sp množinu těch dvojic (a,b)∈M, v nichž je jak a, tak b dělitelné prvočíslem p. Všechny dvojice v Sp jsou tedy soudělné, a naopak každá soudělná dvojice leží v alespoň jedné množině Sp. Platí tedy S = ⋃p Sp, a proto |S| ≤ ∑p |Sp|, kde ∑p sčítá přes všechna prvočísla mezi 2 a N.
Kolik prvků má jedna množina Sp? Ve dvojici (a,b)∈Sp musí být jak a, tak b násobkem p. Celkem tedy máme nejvýše N/p možností pro a a stejně tolik pro b. Proto |Sp| ≤ (N/p)2.
O velikosti množiny S tedy víme, že |S| ≤ ∑p (N/p)2 = N2 ·∑p 1/p2. Tato nerovnost platí i tehdy, sčítáme-li přes úplně všechna prvočísla. Suma ∑p 1/p2 bude kýžená konstanta d, ovšem musíme ukázat, že leží ostře mezi 0 a 1.
| ∞ |
| n=1 |
Pro naši konstantu d jistě platí, že d≤ β. To ale nestačí na d<1. Ovšem když si uvědomíme, že 1/12 a 1/42 jsou v β, ale nejsou v d, dostaneme d ≤ β- 1 - 1/16 ≤ 2 - 1 - 1/16 = 15/16. A to už naše požadavky splňuje.
 35-1-X1 Rejstřík zlomků (Zadání)
35-1-X1 Rejstřík zlomků (Zadání)
Pokračujme v úvahách z řešení úlohy 35-1-4. Hodil by se nám podobný strom, ale uspořádaný podle hodnot zlomků, abychom je uměli vyjmenovat v rostoucím pořadí. Tak si ho pořídíme.
Strom zlomkovník
Nejprve definujeme mediant dvou zlomků a/b a c/d. To je zlomek (a+c)/(b+d). Všimneme si, že pokud platí a/b < c/d, pak mediant leží mezi nimi:
| a |
| b |
| a+c |
| b+d |
| c |
| d |
(snadno ověříme vynásobením společným jmenovatelem).
Pomocí mediantů budeme vytvářet posloupnosti zlomků. Posloupnost A0 obsahuje zlomky 0/1 a 1/0 (ten druhý je naše soukromá reprezentace nekonečna). Posloupnost Ai+1 získáme z Ai tak, že mezi každé dva zlomky vložíme jejich mediant:
| A1 | =
| ||||||||||||||||||
| A2 | =
| ||||||||||||||||||
| A3 | =
|
Z vlastností mediantů plyne, že každá posloupnost Ai je ostře rostoucí.
Vytváření posloupností vkládáním mediantů můžeme také popsat stromem. Říká se mu Sternův-Brocotův strom nebo také strom zlomkovník (rostou na něm přeci zlomky). Jeho prvních pár hladin vypadá takto:
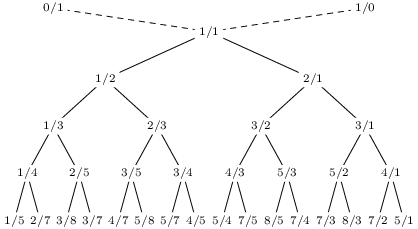
Každý vnitřní vrchol stromu je mediantem svého levého a pravého předka – když jdeme z vrcholu nahoru, první vrchol, do nějž přijdeme zleva, je pravý předek; symetricky levý předek (buď levý nebo pravý předek je otec, druhý předek leží někde výše).
Posloupnost Ai je tedy sjednocením prvních i hladin stromu. Navíc pro libovolný vrchol v platí, že všechny zlomky v levém podstromu pod v jsou menší než zlomek ve v, a ten je menší než všechny zlomky v pravém podstromu. Zlomkovník je tedy uspořádaný jako vyhledávací strom, a proto se v něm žádné racionální číslo neopakuje.
Všechny zlomky ve stromu bychom mohli vypsat v rostoucím pořadí následující rekurzivní funkcí (nenechte se zmást tím, že běží nekonečně dlouho; v praxi bychom samozřejmě rekurzi včas zařízli, a tak vypsali vhodný konečný podstrom). Její parametry jsou zlomek ℓa/ℓb coby levý předek vypisovaného podstromu a zlomek pa/pb coby jeho pravý předek.
Zlomkovník(ℓa/ℓb, pa/pb)
- a ← ℓa + pa, b ← ℓb + pb
- Zlomkovník(ℓa/ℓb, a/b) ◁ levý podstrom
- Vypíšeme a/b.
- Zlomkovník(a/b, pa/pb) ◁ pravý podstrom
Rekurzi spustíme zavoláním Zlomkovník(0/1, 1/0).
Brzy dokážeme, že ve stromu leží všechny zlomky a jsou v základním tvaru. Předtím si ale rozmyslíme, jak pomocí zlomkovníku vyřešit zadanou úlohu.
Řešení úlohy
Zlomkovník budeme používat jako vyhledávací strom. Je trochu nepraktické, že je to strom nekonečný. Jelikož však všechny cesty do „malých“ zlomků s čitatelem i jmenovatelem z {1,… ,N} vedou jen přes další malé zlomky, stačí se prostě pří prohledávání stromu zastavovat o velké zlomky.
Stačí tedy umět vypsat nejmenších K klíčů ve vyhledávacím stromu. Na to si pořídíme rekurzivní funkci, která bude postupně vypisovat klíče a vrátí, kolik jich vypsala:
PrvníchK(v, K)
- Pokud v=∅, vrátíme 0.
- i ← PrvníchK(levý_syn(v), K)
- Pokud i<K:
- Vypíšeme klíč(v).
- i ← i + 1
- Pokud i<K:
- i ← i + PrvníchK(pravý_syn(v), K-i)
- Vrátíme i.
Jak rychlá tato funkce je? Představme si cestu ve stromu mezi kořenem a posledním vypsaným klíčem. Vše nalevo od této cesty bylo vypsáno. Vše napravo je moc velké a vůbec jsme tam nezalezli. Některé vrcholy na cestě jsme vypsali, některé nevypsali, ale těch nevypsaných je nejvýš tolik, kolik je hloubka stromu – v našem případě tedy nejvýš N.
Navštívíme tedy O(N+K) vrcholů, pokaždé v konstantním čase spočítáme, jaký zlomek se tam nachází. Algoritmus má tedy časovou složitost O(N+K), a to je O(K), neboť máme slíbeno, že K≥ N.
Mimochodem, kdyby bylo K malé, stejně si umíme poradit: zlomky na nejlevější cestě ve stromu jsou 1/i, takže bychom rovnou mohli skočit správně hluboko a vypisovat odtamtud. To by dalo složitost O(K) nezávisle na N.
Zlomky jsou v základním tvaru
Zbývá ověřit, že zlomkovník má slíbené vlastnosti.
Indukcí podle i budeme dokazovat, že pro každé dva zlomky a/b a c/d, které sousedí v posloupnosti Ai, platí:
Z toho ihned plyne, že každý společný dělitel čísel a a b musí také dělit bc-ad, pročež jediní společní dělitelé jsou 1 a -1. Čísla a a b jsou tedy nesoudělná. Analogicky jsou nesoudělná i c a d.
Nyní slíbená indukce. Pro A0 tvrzení evidentně platí. Když z Ai vyrábíme Ai+1, mezi každé sousední zlomky a/b a c/d vkládáme (a+c)/(b+d). Tím jsme vytvořili dvě nové dvojice sousedních zlomků. Pro první z nich má platit:
což je po roznásobení totéž jako
To platí, jelikož obě ab se navzájem odečtou a bc-ad=1 je indukční předpoklad.
Podobně pro druhou dvojici sousedních zlomků chceme
což je opět ekvivalentní s bc-ad=1.
Všechny zlomky ve zlomkovníku jsou tedy v základním tvaru.
Cesty ve zlomkovníku
Zlomkovník nám také dává další způsob, jak zapisovat racionální čísla – cestami z kořene. Označíme-li L krok doleva a P krok doprava, bude například LPPL = 5/7. Ukážeme, jak převádět mezi zlomky a cestami.
Jelikož zlomkovník je vyhledávací strom, můžeme každému vrcholu přiřadit nějaký interval (ℓa/ℓb, pa/pb). Všechny zlomky v podstromu leží v tomto intervalu, všechny zlomky mimo podstrom leží mimo interval. Přitom ℓa/ℓb a pa/pb jsou levý a pravý předek vrcholu.
Intervaly budeme popisovat pomocí matic 2×2:
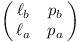
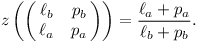
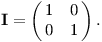
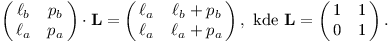
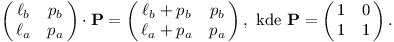
Například
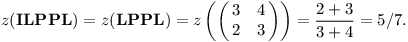
Jelikož zlomkovník je binární vyhledávací strom, můžeme v něm zadaný zlomek vyhledávat rekurzivně: kdykoliv přijdeme do vrcholu se zlomkem větším než hledaný, pokračujeme doleva; když s menším, pak doprava. Můžeme to zapsat následovně, přičemž a/b je hledaný zlomek a V matice reprezentující interval aktuálního vrcholu (na počátku je V=I):
HledejZlomek(a/b, V)
- Opakujeme:
- va/vb = z(V)
- Pokud a/b = va/vb:
- Nalezli jsme a skončíme.
- Pokud a/b < va/vb:
- HledejZlomek(a/b, VL)
- Jinak:
- HledejZlomek(a/b, VP)
Pokud se zlomek a/b ve stromu vyskytuje, tento algoritmus ho najde. Pokud by se nevyskytoval, algoritmus poběží donekonečna a bude se nořit do čím dál užších intervalů obsahujících a/b. (Mimochodem, pokud bychom algoritmus nechali hledat iracionální číslo, najde nekonečnou cestu konvergující k zadanému číslu, na které leží čím dál lepší racionální aproximace. To ale nebudeme dokazovat.)
Na hledání se dá také dívat jinak: místo abychom postupně upravovali matici V, budeme upravovat zlomek a/b.
Všimneme si jedné zajímavé vlastnosti algoritmu. Pokud první krok vedl doprava, ve všech dalších krocích bude platit V = PX, kde X je nějaká matice závislá na aktuálním kroku. Budeme tedy a/b porovnávat s z(PX), které je ovšem pro
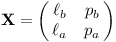
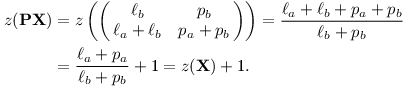
Podobnou úvahu můžeme provést pro krok doleva a rekurzi na(a/b, PV) nahradit za (a/(b-a), V). Odvození nemusíme opakovat, stačí si uvědomit, že prohození kroků doleva a doprava v cestě způsobí prohození čitatele a jmenovatele v cílovém zlomku.
Teď už se v rekurzi matice V nemění a zůstává pořád rovná počáteční jednotkové matici. Test a/b < z(V) je tedy a/b < z(I), což je a/b < 1, tedy a < b.
To je ale přeci Euklidův algoritmus! Pokud je a<b, odečteme a od b, jinak b od a. V jednom případě jdeme doleva, v druhém doprava. Dokázali jsme tedy, že vyhledávání ve zlomkovníku je ekvivalentní s Euklidovým algoritmem. Tím pádem se hledání vždy zastaví, ale to může jen tehdy, pokud zlomek najde. Zlomkovník tedy obsahuje všechny zlomky.
Kouzlo na závěr
Podívejte se na nějakou hladinu zlomkovníku a srovnejte ji s odpovídající hladinou Calkinova-Wilfova stromu z předchozí úlohy. Obsahují tytéž zlomky, jen v jiném pořadí! Důvod je prostý: cesta k určitému zlomku v obou případech odpovídá průběhu Euklidova algoritmu, jen poprvé průběh zapisujeme popředu, podruhé pozpátku. Očíslujeme-li tedy zlomky na k-té hladině jednoho stromu k-bitovými binárními čísly, bude poloha zlomku v jednom stromu rovna poloze v druhém stromu zapsané pozpátku.
 35-1-S Lineární rovnice (Zadání)
35-1-S Lineární rovnice (Zadání)
Úkol 1 – Robot na Marsu [5b]
Označme si vektory na vstupu x, y. Tyto vektory jsou tvořeny dvěma složkami: x = (x1, x2)⊤, obdobně y = (y1, y2)⊤.
Představme si, že se nacházíme na souřadnicích (0,0)⊤. Chceme se pohnout o m metrů dopředu, tedy se dostat na souřadnice v = (m, 0)⊤.
Potřebujeme nalézt lineární kombinaci vektorů x a y takovou, aby výsledný vektor byl roven vektoru v. Tedy chceme nalézt čísla a a b taková, že:
Nyní tuto rovnici můžeme rozepsat po složkách:
Dostali jsme dvě rovnice o dvou neznámých. Tuto soustavu by šlo vyřešit pomocí Gaussovy eliminace, nicméně v tomto případě není těžké zapsat řešení explicitně. Z druhé rovnice vyjádříme b:
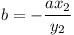
A dosadíme do první rovnice:
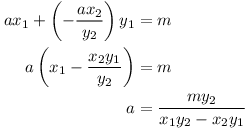
Odtud lze dopočítat i b, povšimněte si symetrie:

Sondě tedy řekneme, aby se pohla o a metrů vpřed a o b metrů doleva. Pohyby pro povel „o m metrů doleva“ spočítáme obdobně.
Pro úplnost je třeba ukázat, že jmenovatel výše uvedených výrazů není nulový. Jsou-li vektory x, y nenulové a mají-li různý směr, poté platí x1 / x2 ≠ y1 / y2, tedy x1 y2 ≠ x2 y1.
Úkol 2 – Nezávislost a soustavy [3b]
Mějme d-rozměrné vektory x1, x2, …, xn, chceme ověřit jejich lineární nezávislost. Prvně si musíme uvědomit, co nezávislost vlastně znamená. Zmiňovali jsme dvě definice, my použijeme tu druhou, tedy že rovnice
| n |
| i=1 |
platí jedině, pokud ai = 0 pro všechna i.
Stačí pracovat s touto rovnicí, konkrétně ji rozepíšeme po složkách. Potřebujeme hodně indexů, výrazem (xi)j značíme j-tou složku vektoru xi.
| a1 (x1)1 + a2 (x2)1 + …+ an (xn)1 = 0 |
| ⋮ |
| a1 (x1)d + a2 (x2)d + …+ an (xn)d = 0 |
Opět dostáváme soustavu rovnic. Řešení ai = 0 bude existovat vždy. Pokud se jedná o jediné řešení, pak jsou vektory nezávislé. Jinak existuje nenulové ai, příslušný vektor můžeme převést na druhou stranu a koeficientem ai rovnici vydělit, čímž dostaneme vyjádření jednoho vektoru jako lineární kombinaci zbytku.
Jednoduché pozorování na závěr: Pokud n > d, pak vždy platí, že vektory jsou lineárně závislé.
Úkol 3 – Algoritmus eliminace [7b]
Samotný algoritmus byl popsaný v zadání, bylo však nutné rozmyslet mnoho implementačních detailů.
Začněme reprezentací soustavy. Jistě dává smysl si ji uložit jako seznam rovnic.
Pro rovnice samotné lze také použít seznamy, pak si budeme muset naimplementovat jejich násobení a sčítání.
Také by šlo využít nějaký vektorový typ, který už tyto operace umí,
v Pythonu například numpy.ndarray.
Je třeba se zamyslet i nad číselným datovým typem. V zadání jsou sice celá čísla, v průběhu výpočtu nám však mohou vzniknout i zlomky. Jako jednoduché řešení se nabízí použít desetinná čísla, pak si ovšem musíme dát pozor na zaokrouhlovací chyby. Hodnoty, které by správně měly být nulové, mohou být nepatrně větší či menší. Vzorové řešení v průběhu eliminace používá celá čísla, tento postup by ale nefungoval pro velké soustavy, kde by čísla ve výpočtech mohla rychle vzrůst.
Pokud soustava nemá jednoznačné řešení, někdy v průběhu eliminace se stane, že ve všech řádcích v aktuálním sloupci budou nuly. Poté není co eliminovat, takže daný sloupec přeskočíme.
To bude mít za důsledek, že koeficient u poslední neznámé v posledním řádku bude nulový. Podle toho tedy jde poznat typ řešení. Ještě se musíme podívat na pravou stranu v poslední rovnici, podle toho rozlišíme soustavu bez řešení a parametrizované řešení.
Zpětná substituce
Jakmile máme eliminaci hotovou, zbývá dopočítat řešení zpětnou substitucí. Doteď stačila celá čísla, nyní již bude nutné použít zlomky.
V jednoznačném případě je výpočet poměrně přímočarý. Stačí procházet rovnice od konce, v každé bude jediná neznámá, zbytek už známe. Převedeme tedy již spočítané neznámé na pravou stranu, čímž vyjádříme tu hledanou.
Parametrizovaný případ je zajímavější, jedna rovnice nám může přidat více nových neznámých. Poté musíme všechny až na jednu prohlásit za parametry.
Při dopočítávání neznámé musíme dopočítat i to, jak závisí na parametrech. K tomu se hodí mít neznámé reprezentované v rovnicovém zápisu a až na konci jej převést na vektorový.
Zbývá jen se zamyslet nad složitostí řešení. Chceme eliminovat polovinu koeficientů, kterých je O(d2). Pokaždé násobíme a sčítáme celé řádky délky O(d), celkem tedy O(d3). Výpočet řešení v jednoznačném případě je O(d2), tolik spočítaných neznámých totiž převádíme na pravou stranu. Parametrizovaný případ se chová podobně, jen pracujeme s vektory místo čísel, takže O(d3). Paměti potřebujeme vždy O(d2).
Gaussova-Jordanova eliminace
Existuje způsob, jak si výpočet řešení trošku zjednodušit. Při eliminaci budeme vytvářet nuly nejen pod aktuálním řádkem, nýbrž i nad ním. Tento postup se nazývá Gaussova-Jordanova eliminace.
Je-li řešení jednoznačné, zbude v každé rovnici pouze jediný koeficient. Pak je vyjádření neznámé triviální, stačí podělit pravou stranu koeficientem.
Je-li řešení parametrizované, pak v rovnici navíc zbudou koeficienty parametrů. Stačí je tedy převést na pravou stranu a rovnou získáme vektorový zápis.
Kvůli vytváření nul i nad aktuálním řádkem provedeme dvakrát tolik operací než při Gaussově eliminaci. Asymptotická složitost ovšem zůstane stejná.