Pátá série třicátého pátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 35-5-1: Písek
- 35-5-2: Hroší lomikámen
- 35-5-3: Nejkrásnější náhrdelník
- 35-5-4: Kalkulačka
- 35-5-S: Determinant
35-5-1 Písek (Zadání)
Začneme s jednodušší verzí úlohy, kde je na pravé straně ostrova nekonečně vysoká zeď. V takovém případě se písek může sesypat pouze z levého okraje.
Nejdříve si spočítáme, v jaké výšce (nad zemí) bude povrch hromady písku. Pro každý dům si ji můžeme reprezentovat jedním číslem – výškou na levém okraji. Od něj bude pokračovat svah s úhlem 45° do pravého okraje, kde bude sahat o patro výš. U nejlevějšího domu je výška písku rovná výšce domu – cokoliv vyššího by se sesypalo přes okraj. Nad dalším domem může svah pokračovat, takže přičteme jedna k předchozí výšce. Dům na tomto místě ale taky může být vyšší, v čemž případě bude začínat nový svah na střeše domu. Pro každý dům tedy bude výška povrchu rovna maximu z výšky domu a minulé výšky zvětšené o jedna.
Spočítat objem písku je pak už jednoduché. Pro každý sloupec odečteme od výšky povrchu výšku domu (písek začíná až nad střechou), vynásobíme čtyřmi (objem jednoho políčka) a přičteme dva za trojúhelníkové půlpolíčko se svahem.
Takto by to vypadalo pro příklad ze zadání:
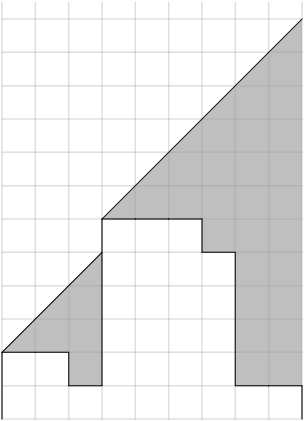
Objem písku je 2 + 6 + 14 + 2 + 6 + 10 + 18 + 38 + 42 = 138.
Nyní se vrátíme k původní úloze, kde se písek sype přes oba kraje. V takovém případě se může písek udržet v dané výšce právě tehdy, když se nesesype z ani jedné strany. Můžeme tedy ostrov projít z obou směrů, spočítat maximální výšku písku, ve které se nesesype z dané strany, a vzít minimum z těchto hodnot. Pokud jsou výšky v daném sloupci ze dvou směrů různé, tak se nižší svah celý vejde pod ten vyšší a výpočet objemu bude stejný. Pokud jsou ale stejné, svahy se uprostřed zkříží a místo dvou budeme přičítat jenom jedna.
Takto by to vypadalo pro příklad ze zadání:
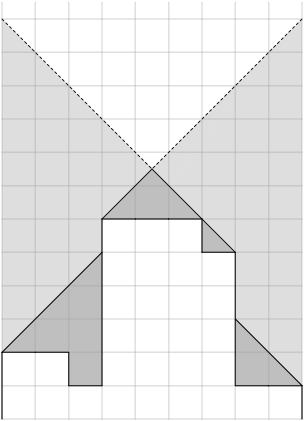
Objem písku je 2 + 6 + 14 + 2 + 5 + 2 + 2 + 6 + 2 = 41.
Celý algoritmus je jen několik průchodů ostrova, kde pro každý dům provedeme výpočet v konstantním čase, takže časová složitost je O(N). Obdobně to platí i pro paměťovou složitost.
35-5-2 Hroší lomikámen (Zadání)
Co po nás úloha doopravdy chce? Máme dva řetězce A a B a máme najít u každého stejně dlouhý podřetězec, přičemž v tomto podřetězci má být rozdíl stejných a různých písmen maximální.
Nabízí se jednoduchý algoritmus, kde pro každou možnost relativního posunutí začátku podřetězce v A a v B vyzkoušíme všechny začátky a konce. Mohli bychom počítat počet rozbitých kamenů v tomto podřetězci postupným procházením, ale všimněme si, že dvojice stejných kamenů nám dá +2, zatímco dvojice různých -2 a my hledáme součet úseku. Na to můžeme použít prefixové součty, díky kterým spočteme součet v konstantním čase.
Co ale vlastně děláme? Hledáme úsek s největším součtem vyzkoušením všech možností. Toto můžeme ale zrychlit. Protože součet úseku od ℓ po r v prefixových součtech je p[r] - p[ℓ], tak dává smysl vybrat nejmenší p[ℓ].
Jen si musíme dát pozor, aby platilo ℓ< r. Takže budeme pole prefixových součtů postupně procházet, udržovat si nejmenší doposud nalezené p[ℓ] a to vždy odečteme od aktuálního p[i]. Díky tomu najdeme nejlepší začátek a konec v lineárním čase.
To budeme dělat pro každou možnost posunu, což nám dá výslednou časovou složitost O((N+M)min(N, M)) = O(NM).
35-5-3 Nejkrásnější náhrdelník (Zadání)
Jak úlohu řešit přímočaře? Vygenerujeme si všechny možnosti, kam dát zapínání, a potom je všechny porovnáme a vybereme maximum. Např. pro náhrdelník 3, 1, 3, 2 by možnosti byly:
| 3, 1, 3, 2 |
| 1, 3, 2, 3 |
| 3, 2, 3, 1 |
| 2, 3, 1, 3 |
Maximální je třetí z nich.
Obecně by to celé trvalo O(N2). Na vygenerování spotřebujeme O(N2) času a porovnávání trvá O(N) na sousední dvojici.
Pojďme to ale zlepšit. Pro začátek nepotřebujeme všechny možnosti generovat, ale můžeme si prostě udržovat indexy do náhrdelníku bez zapínání.
Nyní pojďme všechny možnosti porovnávat současně. Udržujme si množinu aktuálních možností, kde možnost je reprezentována aktuálním indexem a indexem začátku. (Na začátku všechny možnosti budou tvaru i, i.) Poté vždy vyškrtněme možnosti, které nebudou největší. Najděme maximální prvek na aktuálním indexu a zahoďme všechny možnosti, které ho nemají.
Pojďme se podívat, jak se tento algoritmus vyvíjí na ukázkovém vstupu:
Bohužel, tento algoritmus je stále pomalý. Uvažme vstup 3, 3, …, 3, 1. V první fázi projdeme n možností, v druhé n-1, ...
Pojďme to opravit trochu jiným pohledem na věc. V algoritmu si budeme udržujeme úseky – to jsou části délky k, které jsou největší k-tice v zadané posloupnosti. V předchozím algoritmu se nám úseky mohly překrývat, ale tentokrát jim to zakažme.
Na začátku si vytvořme úseky délky 1, které obsahují maximální prvek. (Každý maximální prvek odpovídá úseku.) Nyní je všechny zkusme prodloužit.
Buď nově přidávané číslo vždy není součástí úseku, pak přidejme ty čísla, která jsou maximální. (Ostatní úseky nám „umřou“ – nebudou se dále prodlužovat.)
Jinak nám některé úseky narazí do následujících. Protože začátek úseku je vždy maximální číslo (a opačně), tak ty, co nenarazily, nám umřou, a ty co narazily, nechť pohltí úsek přímo za nimi (a usmrtí ho v případě nutnosti). Po pohlcení nám též umřou ty úseky, které nejsou nejdelší z živých (delší úsek je z definice maximální k-tice, takže za kratším je menší číslo).
Zde se nám může stát, že všechny živé úseky (s délkou p) do sebe narazí cyklicky. Pak posloupnost je periodická s periodou p a jako odpověď stačí vydat začátek libovolného úseku.
Jinak opakujeme výše popsané prodlužování, dokud nám nezbude jen jeden úsek. Pak ten je jistě naší odpovědí, protože neexistuje větší k-tice se stejnou délkou, tedy ani delší.
A jakou toto bude mít složitost?
- Každé číslo bude přidáno nejvýše jednou.
- Každý úsek zemře nejvýše jednou.
- Každý úsek bude pohlcen nejvýše jednou (pak bude pohlcen i s tím úsekem, co ho pohltil).
Každá věc se při prodlužování stane nejvýše O(N)-krát, a proto algoritmus poběží v lineárním čase.
Dva kanóny na vrabce
Jako ochutnávku na závěr zmíníme dvě silné techniky, ze kterých nám jen tak
mimochodem vypadnou řešení v O(N log N) čase. O obou si víc můžete přečíst
v Průvodci labyrintem algoritmů. Obě techniky pracují s řetězci,
a proto o naší posloupnosti nyní budeme jako o řetězci přemýšlet. V obou
případech se nám také hodí zbavit cykličnosti, a proto si náš řetězec
zapíšeme dvakrát za sebou. Pak mezi všemi jeho podřetězci délky N hledáme ten
lexikograficky největší.
První technikou jsou tzv. suffixová pole, která umí vzít libovolný řetězec a seřadit všechny jeho možné suffixy (podřetězce začínající někde v řetězci a končící na jeho konci) podle jejich lexikografického pořadí. Výstupem je pole, kde na pozici i je uložené, kde začíná i-tý lexikograficky nejmenší suffix. Lidová moudrost praví, že se suffixovými poli (a jejich příbuzným, suffixovými stromy) jde skoro libovolná řetězcová úloha vyřešit v lineárním čase.
Tak tomu (až na logaritmus navíc) je i u nás: nejkrásnější umístění zapínání totiž téměř přesně odpovídá lexikograficky největšímu suffixu naší posloupnosti. Má to jen jeden háček: zatímco my hledáme podřetězec délky N, suffixové pole nám seřadí suffixy délky 1 až 2N. Můžeme si ale rozmyslet, že suffixy délky menší než N můžeme ignorovat, a že ty zbylé budou ve správném pořadí i vzhledem jen k jejich prvních N znakům. Stačí tedy procházet suffixové pole odzadu a zastavit se u prvního suffixu délky větší než N. To umíme v lineárním čase, a spolu s konstrukcí suffixového pole (nad řetězci s neomezeně velkou abecedou) tak dostáváme řešení v čase O(N log N).
Druhá technika využívá tzv. okénkové hešování – techniku, pomocí které si pro náš řetězec umíme předpočítat jakési „prefixové součty“ – akorát s heši místo se součty. Umíme se pak v O(1) zeptat na libovolný podřetězec a obdržet zpátky jeho heš – číslo s tou vlastností, že dva stejné řetězce vždy dostanou ten samý heš, a různé řetězce s velmi velkou pravděpodobností (řekněme 1 - n-10) dostanou různý heš. Dovolíme-li algoritmu nějakou malou pravděpodobnost chyby, umíme pak rychle testovat, zda se dva podřetězce rovnají – stačí porovnat jejich heše a doufat, že jsme zrovna neměli smůlu a nenarazili na dva různé řetězce se stejným hešem.
Jak s okénkovým hešováním vyřešit úlohu? Vcelku jednoduše: nyní můžeme pro dva podřetězce délky N v čase O(log N) zjistit, který z nich je lexikograficky větší: stačí kombinací binárního vyhledávání a okénkového hešování najít první místo, kde se neshodují, a podívat se, který z nich má na tomto místě větší hodnotu. A tím už máme vyřešenou celou úlohu: stačí postupně brát podřetězce [0, N), [1, N + 1), … , [N, 2N) a každý porovnat s aktuálně lexikograficky největším. Tak N-krát provedeme binární vyhledávání a časová složitost je O(N log N).
35-5-4 Kalkulačka (Zadání)
Stavy kalkulačky si můžeme představit jako nekonečný orientovaný graf. Pokud se dá nějaké číslo převést operací na , existuje v tomto grafu mezi vrcholy odpovídajícími a hrana. Nás zajímá minimální počet operací, kterými z nějakého z čísel dostaneme . Tedy vlastně nejkratší cesta mezi libovolným z vrcholů k vrcholu odpovídajícímu . Tu můžeme najít s pomocí BFS, přičemž za výsledek prohlásíme první cestu, kterou najdeme. Ta bude jistě nejkratší, protože BFS se chová tak, že vždy prozkoumává vrcholy v bližších vzdálenostech a pak až v těch vzdálenějších.
Ale jak uložit nekonečný graf? Jednoduše: nebudeme ho ukládat. Hrany a vrcholy budeme vytvářet až za běhu, když do nich dojdeme. Tomu se říká prohledávání implicitního grafu.
Nyní pojďme rozebrat složitost. Nejprve najdeme horní odhad počtu potřebných operací, k čemuž se nám bude hodit reprezentovat čísla v devítkové soustavě. Pak můžeme čísla zapsat do kalkulačky po číslicích, např. číslo (již zapsané v devítkové soustavě) bychom zapsali jako . Na každou cifru tedy potřebujeme dvě operace plus jednu na poslední přičtení. Jakékoli číslo tedy můžeme na kalkulačce získat tak, že ho převedeme do devítkové soustavy a pak dané číslo vložíme výše uvedeným způsobem do kalkulačky. Např. je v devítkové soustavě a . Číslo tedy určitě lze vyrobit na operací.
Prohledávání se tedy může dostat jenom do vrcholů, které jsou nejvýše takto daleko od počátku. To nám dá i horní odhad časové složitosti: z každého vrcholu vede konstantní počet hran, takže jedním vrcholem strávíme konstantní čas.
Nepotkáme tedy čísla větší než (i kdybychom opakovaně násobili ). Navíc nemusíme prozkoumávat čísla větší než , protože by nám pak trvalo ještě přibližně kroků, abychom ho znovu snížili (abychom se dostali ke ).
Tedy finální složitost vychází jako .
35-5-S Determinant (Zadání)
Úkol 1 – Obsah mnohoúhelníku [6b]
Pro začátek si uvědomíme, jak spočítat obsah trojúhelníku mezi body p1, p2, p3. Vyrobíme vektory x = p2 - p1 a y = p3 - p1. Následně pomocí determinantu spočítáme obsah rovnoběžníku určeného vektory x a y. Obsah trojúhelníku bude polovina obsahu rovnoběžníku.
Jakmile toto umíme, spočítat obsah konvexního mnohoúhelníku již zvládneme hravě. Rozdělíme mnohoúhelník na trojúhelníky a jejich obsah sečteme.
Rozdělení lze elegantně realizovat takto: Vezmeme tři po sobě jdoucí vrcholy, spočítáme obsah trojúhelníku mezi nimi a tento trojúhelník z mnohoúhelníku odštípneme vynecháním prostředního vrcholu. Tento postup opakujeme, dokud jsou v mnohoúhelníku alespoň tři vrcholy.
Pokud budeme brát vrcholy vždy v pořadí po obvodu, znaménko determinantu bude pro každý trojúhelník stejné. Pokud nám vyjde záporný součet, stačí jako výsledný obsah vzít jeho absolutní hodnotu.
Co když mnohoúhelník není konvexní? Tentýž postup bude stále fungovat. Kdykoli totiž vytyčíme trojúhelník vně mnohoúhelníku, bude mít opačné znaménko. Vynecháním prostředního bodu jím mnohoúhelník doplníme.
Spočítání obsahu jednoho trojúhelníku trvá konstantní čas. Kroků provedeme méně, než kolik je vrcholů, takže dostáváme celkovou časovou složitost O(N).
Ještě ve zkratce uvedeme alternativní řešení. Zvolíme si libovolný bod z, pro jednoduchost z = (0, 0). Poté sečteme obsahy trojúhelníků zp1p2, …, zpN-1pN, zpNp1 a vezmeme absolutní hodnotu tohoto součtu. Podobně jako dříve platí, že se části uvnitř mnohoúhelníku započítají kladně a části vně mnohoúhelníku záporně.
Úkol 2 – Polynom [6b]
Nechť má polynom předpis p(x) = a2x2 + a1x + a0, kde a2, a1, a0 jsou neznámé koeficienty. Aby polynom procházel zadanými body, musí platit následující rovnice:
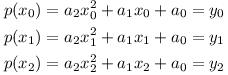
Zapíšeme-li tuto soustavu maticově jako Ax = y, matice A bude vypadat následovně:
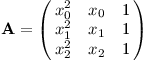
Aby byl polynom jednoznačně určený, determinant matice A musí být nenulový.
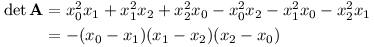
Každá závorka je nenulová, proto je nenulový i celý determinant.
Úkol 3 – Součin [3b]
Nahlédneme vztah pomocí zobrazení. Víme, že determinant matice zobrazení popisuje, kolikrát se tímto zobrazením zvětší obsah.
Mějme obrazec s obsahem S. Zobrazme jej nejprve maticí B, tím se jeho obsah změní na S · det B. Poté jej zobrazme maticí A, tím se jeho obsah změní na S · det A · det B.
Totéž jsme však mohli popsat jedním složeným zobrazením s maticí AB. Toto zobrazení musí zvětšit obsah stejným způsobem, proto det AB = det A · det B.
Stejný argument můžeme použít pro matice rozměrů n×n, jen použijeme zobrazení mezi prostory dimenze n. Determinant matice zobrazení popisuje, jak se změní n-rozměrná analogie objemu, což bychom mohli nahlédnout stejně jako v případě obsahu.