Pátá série třicátého pátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám páté a poslední číslo hlavní kategorie 35. ročníku KSP.

Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Také na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál na lineární algebru.

Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.

Odměny & na Matfyz bez přijímaček

• Termín série: 25. června 2023 ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Sladkou odměnu si vyslouží ten, kdo získá alespoň 2 body z každého dílu seriálu.

Zadání úloh

• 35-5-1: Písek
• 35-5-2: Hroší lomikámen
• 35-5-3: Nejkrásnější náhrdelník
• 35-5-4: Kalkulačka
• 35-5-S: Determinant

35-5-1 Písek (9 bodů)

Kalder je magická země s létajícími ostrovy a pískovými dešti. Kaldeřané většinu roku žijí v obřím městě pokrývajícím celý jeden létající ostrov. Na léto, kdy jsou písečné deště nejsilnější, se přesouvají do pobřežní osady s přívětivějším podnebím. Když se pak na podzim vrací do města, celý ostrov je pokrytý pískem. Pomozte jim spočítat, kolik budou muset odklízet písku.

Město tvoří řada domů různých výšek. Na všech místech dopadá písek a hromadí se tam. Konkrétně zrnko písku je stabilní, pokud má pod sebou tři zrnka písku (tedy vzniká svah s úhlem 45°). Jinak se začne sypat ze svahu do stran. Za okraji města ostrov končí a písek se tam sesype dolů. Každé políčko – jeden dům krát jedno „patro“ – má objem čtyři. Spočítejte maximální objem nahromaděného písku.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete kladné celé číslo N udávající šířku ostrova. Na dalším řádku dostanete N nezáporných celých čísel určující výšky jednotlivých domů.

Formát výstupu: Na výstup vypište jedno číslo – objem nahromaděného písku.

9
2 2 1 6 6 6 5 1 1

41

Takto by vypadala odpovídající hromada písku:

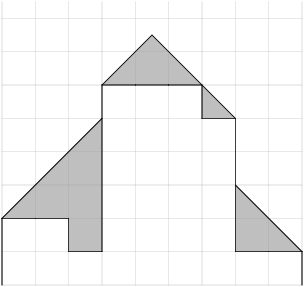
Skládá se ze tří částí, které mají 5.5, 2.75 a 2 políčka. Dohromady to je 10.25 políček, což má objem 41.

Řešení

35-5-2 Hroší lomikámen (12 bodů)

Kláře se po nedávném sesuvu půdy přivalila na zahrádku spousta kamení. Následkem toho se z její zahrádky stala hotová skála.

Klára by se kamenů ráda zbavila pomocí lomikamene hrošího (Saxifraga hippoflora) rostoucího vysoko v Hrochlebských horách. Jak už název napovídá, odvar z této byliny dává člověku hroší sílu drtit kameny holýma rukama.

Síla hrošího lomikamene však skýtá jedno úskalí – člověk s ním dokáže drtit kámen pouze o jiný kámen stejného druhu. Lze tedy takto například o sebe rozbít dva acháty, ale už ne achát s kalcitem.

Kameny jsou na zahrádce popadané ve dvou řadách. Pro jednoduchost jsou všechny kameny stejně velké, takže kameny v jedné řadě lze zarovnávat vůči kamenům v řadě druhé.

Klára by chtěla vždy kámen z jedné řady rozbít o kámen z druhé řady. Aby takto rozbila co možná nejvíce kusů, může si pomoct a nejprve první řadu posunout o libovolný celočíselný počet kamenů dopředu či dozadu.

Následně si z první řady vybere kámen, od kterého začne svou destruktivní procházku. Počínaje ním obejde každý kámen v první řadě a srovná jej s kamenem naproti němu v druhé řadě. Pokud budou stejného druhu, Klára je díky čaji z hrošího lomikamene oba rozbije, jinak je nechá na pokoji (sem spadá i případ, kdy kámen v protější řadě neexistuje). Následně se posune o jeden kámen dopředu a postup opakuje. Pokud Klára uzná, že už se jí rozbíjení kamenů nevyplatí, může s obcházením kdykoliv skončit.

Klára by ráda maximalizovala rozdíl počtu rozbitých a nerozbitých kamenů na své procházce. Pomůžete jí určit, jak by měla jednotlivé řady posunout, od kterého kamene začít a jak dlouho bude chtít kontrolovat?

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete dvě kladná celá čísla N, M udávající délky dvou řad. Na dalších dvou řádcích dostanete dva řetězce o délkách N a M reprezentující dvě řady kamení. Znak x na i-té pozici řetězce udává, že v příslušné řadě je i-tým kamenem druh s názvem x. Názvy druhů jsou výhradně malá písmena anglické abecedy.

Formát výstupu: Na výstup vypište mezerou oddělená čtyři celá čísla A, B, C, D. Hodnota A nechť značí vámi nejvyšší nalezený rozdíl počtu rozbitých a nerozbitých kamenů. Dále celé číslo B bude udávat, o kolik kamenů dopředu by měla Klára posunout první řadu kamení. Hodnota B může být libovolně velká (tedy i klidně záporná).

Hodnoty C, D zase budou říkat, na které pozici v první řadě bude chtít Klára s kontrolou začít a na které bude chtít skončit (včetně), aby maximalizovala celkový rozdíl rozbitých a nerozbitých kamenů. Musí platit 0 ≤ C ≤ D < N. Řetězce tedy indexujeme od nuly.

8 7
promenka
kamejka

6 -1 3 7

V uvedeném vstupu má Klára dvě řady kamenů. V první řadě leží p(ískovec), r(ubín), o(pál), m(agnezit), … V druhé řadě leží k(alcit), a(chát), m(agnezit), … Jedním způsobem, jak dosáhnout největšího možného rozdílu rozbitých a nerozbitých kamenů, je posunout první řadu o 1 kámen dozadu (tj. o -1 kámen dopředu) a začít postupně rozbíjet kameny ve druhé řadě naproti 3. až 7. kameni v první řadě.

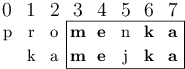
Tím o sebe rozbije dva m(agnezity), dále pár e(meraldů), přeskočí 5. pozici s n(efritem) a j(adeitem) a nakonec ještě rozláme pár k(alcitů) a a(chátů). Celkový rozdíl počtu rozbitých a přeskočených kamenů na Klářině vymezené procházce tedy bude 8-2=6.

Řešení

35-5-3 Nejkrásnější náhrdelník (12 bodů)

Za devatero horami a devatero řekami bylo nebylo jedno království. A protože to bylo království šperkařů, tak místní král zaslíbil princeznu tomu šperkaři, který vyrobí nejkrásnější náhrdelník. Honza z Černého kopce se rozhodl, že ruku princezny získá pro sebe. Proto vyrobil překrásný náhrdelník. Jen nevěděl, jak splnit co nejlépe místní standardy krásy. Pomůžete mu?

Náhrdelník si můžeme představit jako cyklickou posloupnost drahokamů (tedy po posledním drahokamu následuje první) a mezi prvním a posledním má náhrdelník zapínaní. Krásnější z dvou náhrdelníků dostaneme tak, že se podíváme na drahokamy vpravo od zapínání. Pokud jeden je krásnější, pak náhrdelník s ním je krásnější. V opačném případě budeme porovnávat další drahokamy v řadě, než najdeme dva rozdílné.

Honza už vyrobil skoro hotový náhrdelník, jen ještě neudělal zapínání. Pokud Honza zapínání dá mezi k-1 a k-tý drahokam, pak se drahokamy budou porovnávat v pořadí:

Náhrdelník má přední stranu, tedy nelze posloupnost drahokamů otáčet.

Poraďte mu, kde má náhrdelníku udělat zapínaní, tak aby vyšel co nejkrásnější náhrdelník.

7
3 1 2 3 2 1 3

7

Nejlepší je dát zapínání před poslední – sedmý drahokam, čímž nám vznikne náhrdelník 3, 3, 1, 2, 3, 2, 1.

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

Řešení

35-5-4 Kalkulačka (12 bodů)

Vítek našel na půdě svého dědečka starou mechanickou kalkulačku DekaMax pracující v desítkové soustavě.

Ta funguje tak, že člověk do ní nejprve zadá jednu desítkovou cifru (0 až 9) a kalkulačka od té doby už po dobu svého počítání pořád obsahuje nějaké číslo. Poté vždy zadá jednu z následujících operací:

• sčítání
• odčítání
• násobení
• celočíselné dělení (zaokrouhlujeme k nule)
• modulo (neboli zbytek po dělení)

A potom další desítkovou cifru, přičemž se tato operace okamžitě provede a uloží.

Protože je však kalkulačka už poměrně stará, vyžaduje ke své práci promazávat, přičemž jedna operace stojí jeden mililitr oleje. Vítek by rád s kalkulačkou provedl nějaký komplikovanější výpočet. K tomu potřebuje nejprve do kalkulačky uložit celé číslo K. Nemá ale k dispozici příliš mnoho oleje. Proto by byl nejradši, kdyby ho nastavování čísla K stálo co nejméně oleje.

Pomůžete mu nastavit číslo K s co nejmenší spotřebou? Časovou složitost svých řešení odhadujte vzhledem ke K.

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

Řešení

35-5-S Determinant (15 bodů)

Právě čtete poslední díl seriálu. Pokud jste předchozí díly neřešili, pro pochopení následujících odstavců je vhodné si je přinejmenším přečíst. Navíc je stále možné odevzdávat úlohy z nich za polovinu bodů.

Výpočet obsahu

V minulém dílu jsme se naučili počítat délky a úhly, nyní přidáme obsah a objem. Pro začátek se podívejme na obsah rovnoběžníku určeného dvěma vektory.

Vektory zapíšeme do řádků matice:

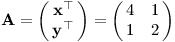
Obsah rovnoběžníku zjistíme z determinantu této matice det A. Pojďme odvodit, jak by se měl determinant počítat.

Začneme u čtverce se stranou délky 1, který by měl mít obsah 1. Takový čtverec se dá popsat jednotkovou maticí, takže det E = 1. Pokud jej v jednom směru protáhneme k-krát, obsah také vzroste k-krát.

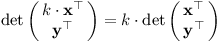
Konkrétně obsah obdélníku zarovnaného s osami bude součin prvků na diagonále:

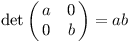
Z geometrie víme, že obsah rovnoběžníku se dá spočítat jako součin strany a výšky na danou stranu. Pokud bychom v rovnoběžníku na obrázku výše posouvali vektor y doleva a doprava, výška by zůstávala stejná, tudíž ani obsah by se neměnil. Obdobně, pokud zafixujeme y, můžeme posouvat x po rovnoběžce s y. V matici se tento fakt projeví tím, že přičtením jednoho řádku k druhému se determinant nezmění:

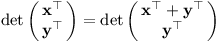
To je vše, co potřebujeme znát. Jakmile umíme vynásobit řádek a sčítat řádky mezi sebou, dokážeme pomocí Gaussovy eliminace převést matici do diagonálního tvaru, jehož determinant již spočítáme snadno.

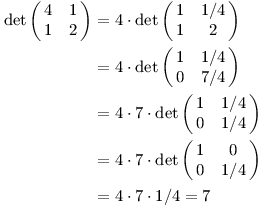
Výpočet výše je rozepsaný detailně, jinak si můžeme dovolit rovnou přičíst násobek řádku. Ve skutečnosti stačilo dojít do druhého kroku, tedy do tvaru, kdy jsou nuly v levé spodní části matice. Nulování prvků v pravé horní části již součin diagonály nezmění.

Znaménko

Ještě musíme uvést na pravou míru jednu věc. Determinant může být i záporný, neboť odpovídá orientovanému obsahu. Nastalo by to v případě, že by vektor x ležel vlevo od y. Prohození vektorů tedy otočí znaménko:

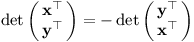
Zajímá-li nás obsah geometrického útvaru, většinou tak vezmeme absolutní hodnotu determinantu.

Úkol 1 – Obsah mnohoúhelníku [6b]

Dostanete zadané vrcholy p₁, …, p_n mnohoúhelníku v rovině. Spočítejte jeho obsah. Bude vhodné jej nějak rozdělit.

Lehčí varianta (za 4 body): Můžete předpokládat, že mnohoúhelník je konvexní.

Více dimenzí

Stejným způsobem jako výše lze spočítat i objem, respektive ekvivalentní veličinu ve více dimenzích. Stačí vzít n vektorů z Rⁿ, zapsat je do řádků matice n×n a spočítat determinant.

Prohození libovolných dvou řádků otočí znaménko. Ve třech dimenzích vyjde determinant kladný, tvoří-li vektory pravotočivou soustavu.

Chcete-li, zamyslete se, jak by se změnilo vaše řešení úkolu výše, pokud bychom místo obsahu mnohoúhelníku počítali objem mnohostěnu.

Pomocí determinantu můžeme například zjistit, jestli bod u leží v rovině určené vektory x, y. Pokud ano, rovnoběžnostěn určený vektory x, y, u bude mít nulový objem.

Permutace

Determinant lze definovat i jinak, totiž pomocí permutací. Pro malé matice je tento náhled jednodušší, proto si jej nyní ukážeme.

Již víme, že determinant matice, která má prvky pouze na diagonále, bude součin těchto prvků. Pokud dostaneme matici, která má v každém sloupci a každém řádku právě jeden nenulový prvek, prohazováním řádků ji zvládneme upravit na diagonální matici. Každé prohození však otočí znaménko, takže pokud jsme provedli lichý počet prohození, součin ještě musíme vynásobit -1.

Determinant plné matice se poté spočte následovně: Uvážíme všechny možnosti, jak vybrat z matice prvky tak, aby v každém řádku a sloupci byl právě jeden. Pro každou možnost spočteme součin těchto prvků, případně vynásobíme -1, a mezivýsledky sečteme.

Vybírání prvků si můžeme představit tak, že přiřadíme každému sloupci jedno z čísel 1 až n, čímž určíme číslo sloupce, ve kterém bude vybraný prvek. Každá možnost tedy odpovídá jedné permutaci n čísel, všech možností je proto n!.

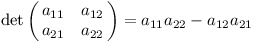
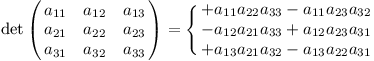
Odvození této alternativní definice najdete na konci textu.

Regularita

Pokud jsou řádky matice lineárně závislé, po eliminaci bude poslední řádek obsahovat samé nuly. Tím pádem bude součin diagonály, tedy i celý determinant nulový. Naopak, pokud jsou řádky lineárně nezávislé, bude na každé pozici na diagonále nenulový prvek. To znamená, že determinant je roven nule právě tehdy, když jsou řádky matice lineárně závislé, tedy když matice není regulární.

Determinant se proto dá použít k ověření, jestli má soustava rovnic jednoznačné řešení. Například pomocí něj umíme zjistit, kdy budou mít dvě přímky v rovině průsečík. Přímky jsou dány rovnicemi a₁ x + b₁ y = c₁ a a₂ x + b₂ y = c₂, hledáme proto řešení x, y této soustavy.

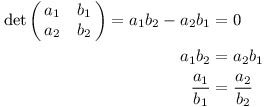
Vyšlo nám, že pokud mají obě přímky stejnou směrnici, pak je determinant nulový a řešení není jednoznačné. Opravdu, rovnoběžky buď nemají žádný průsečík, nebo splývají.

Úkol 2 – Polynom [6b]

Mějme 3 body v rovině (x₀, y₀), (x₁, y₁), (x₂, y₂), pro které platí x₀ < x₁ < x₂. Chceme najít polynom stupně nejvýše 2, který prochází všemi těmito body. Ukažte, že takový polynom bude vždy jednoznačně určený.

Nápověda: Rozložte determinant na součin.

Zobrazení

Poznatek o vztahu determinantu k obsahu a objemu se projeví i u lineárních zobrazení. Uvažme zobrazení popsané maticí z úvodu dílu:

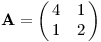
Jednotkový vektor (1, 0)^⊤ se zobrazí na (4, 1)^⊤, obdobně (0, 1)^⊤ se zobrazí na (1, 2)^⊤. Jak se změnil obsah rovnoběžníku určeného těmito vektory? Původně to byl čtverec s obsahem 1, po zobrazení bude obsah  det A.

Úplně stejně se změní obsah jakéhokoli obrazce. Pokud měl původně obsah S, jeho obraz bude mít obsah S · det A.

Úkol 3 – Součin [3b]

Determinant součinu lze spočítat jednoduše:

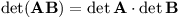
Ukažte, proč tento vztah platí. Váš důkaz nemusí být formální, stačí náhled.

Ortogonální matice

Některá zobrazení zachovávají obsah obrazců. Jsou to taková, pro jejichž matici platí det A = ±1. Mohli bychom chtít ještě trochu více, totiž aby zobrazení zachovávalo i úhly a délky. Přesně to splňují zobrazení popsaná ortogonální maticí.

Matici Q nazveme ortogonální, pokud platí Q^⊤Q = E. Na maticové násobení lze pohlížet jako na mnoho skalárních součinů. V tomto případě požadujeme, aby skalární součin řádku matice se sebou samým byl roven 1, tedy aby měl tento vektor jednotkovou délku. Dále skalární součin řádku s jiným řádkem má být 0, tedy vektory na sebe musí být kolmé.

Vektory kanonické báze mají všechny jednotkovou délku a jsou na sebe kolmé. Zobrazení popsané ortogonální maticí tuto vlastnosti zachovává. Ve výsledku tedy prostor jen otáčí a zrcadlí.

Ortogonální je například matice rotace, se kterou jsme se již setkali ve druhém dílu:

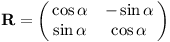
Tato matice opravdu zachovává obsah:

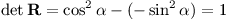
Magické aplikace

Determinant se objevuje v mnoha místech, kde bychom jej nečekali. Zde nabízíme malou ochutnávku.

• Pokud sestavíme trochu upravenou matici sousednosti neorientovaného grafu, odebereme z ní libovolný řádek a libovolný sloupec a spočítáme determinant, dostaneme počet koster grafu.(více)
• Uvažme kružnici určenou body (x_a, y_a), (x_b, y_b), (x_c, y_c). Pokud je determinant následující matice kladný, tak bod (x_d, y_d) leží uvnitř kruhu, pokud záporný, leží vně.
  

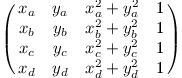
Kromě toho existují variace na determinant, které se počítají podobně a které také mají spoustu využití.

Vztah mezi definicemi

Výpočet determinantu jsme založili na měření objemu. Jak z tohoto pohledu získat definici pomocí permutací?

Budeme potřebovat ještě jednu vlastnost: Pokud zafixujeme všechny řádky matice až na jeden, determinant je v tomto řádku lineární:

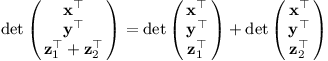
Proč? Uvažme rovnoběžník vymezený vektory x a y. Objem celého rovnoběžnostěnu spočítáme jako součin obsahu rovnoběžníku a výšky na něj. Výška je složka vektoru z₁, respektive z₂ kolmá na rovnoběžník. Sečteme-li tyto vektory, sečtou se i výšky.

Díky této vlastnosti můžeme každý řádek rozepsat na součet vektorů, z nichž každý má jedinou nenulovou hodnotu:

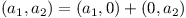
Nejprve rozepíšeme první řádek, poté v každé vzniklé matici rozepíšeme druhý řádek, atd. Tím nám z matice n×n vznikne nⁿ matic, přičemž každá z nich bude mít v každém řádku jediný nenulový prvek.

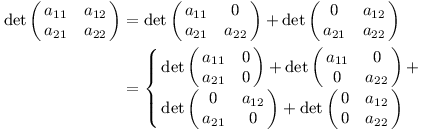
Některé vzniklé matice budou obsahovat nulový sloupec, tudíž i jejich determinant bude nulový. Pouze n! matic bude mít nenulový determinant, ty odpovídají všem možným permutacím.

David Klement

Řešení