Třetí série třicátého pátého ročníku KSP
Celý leták v PDF.
Dostává se k vám třetí číslo hlavní kategorie 35. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Také na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál na lineární algebru.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: 19. února 2023 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo nám k řešení přiloží ručně kreslený obrázek hrošíka. Hrošík by měl vykonávat nějakou netriviální činnost, představivosti se meze nekladou :). Pokud řešení odevzdáváte elektronicky, můžete nám oskenovaný obrázek poslat emailem na známou adresu.
Zadání úloh
- 35-3-1: Čajovod
- 35-3-2: Hroší hortenzie
- 35-3-3: Prodlužovačky
- 35-3-4: Záchrana listí
- 35-3-S: Vektorové prostory
- 35-3-X1: Obvody
 35-3-1 Čajovod (10 bodů)
35-3-1 Čajovod (10 bodů)
Ondra dostal práci v perspektivní technologické firmě. Programátoři si zde velmi potrpěli na kvalitu čaje, a tak se vedení rozhodlo postavit centrální ohřívárnu – zde se čaj připravuje. Dále bylo z ní zapotřebí čaj distribuovat čajovodem, který dostal na starosti právě Ondra.

Jak se brzy dozvěděl, čajovod sestává z uzlů a trubek mezi nimi. Každá trubka spojuje dva uzly. Poté máme (kromě obyčejných) speciální typy uzlů – ohřívárnu a místnosti. V ohřívárně se vyrábí čaj a v místnostech se čaj může spotřebovávat. V místnostech čajovod vždy končí – do každé z nich vede jen jedna trubka. Kromě toho z ohřívárny se do každého uzlu může čaj dostat právě jednou posloupností trubek a uzlů. Formálně čajovod tvoří strom, ohřívárna se nachází v kořeni a místnosti v listech.
Není to ale tak jednoduché. V místnostech buď sedí programátoři, manažeři, nebo jsou prázdné. Pokud v místnosti sedí programátoři, je zapotřebí, aby tam čaj dotekl. Naopak manažeři pijí kafe, a proto do místností s manažery téct čaj nesmí. U prázdných místností je to jedno.
Aby se tok čaje dal regulovat, na každé trubce je uzávěr, který je buď otevřený, nebo uzavřený, a podle toho skrz ni teče, nebo neteče čaj. Čaj doteče do místnosti, když všechny trubky z ohřívárny k ní jsou otevřené. Ondra potřebuje popřehazovat některé uzávěry tak, aby do místností tekl čaj, podle toho, kdo tam je. Aby se co nejméně napracoval, rád by jich změnil co nejméně. Pomůžete mu?
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete dvě čísla, počet uzlů N a počet místností M. Ohřívárna se nachází v uzlu číslo 1.
Na dalších N-1 řádcích dostanete dvě čísla uzlů, mezi kterými vede příslušná trubka, a znak O, když je otevřená, jinak Z.
Na posledních M řádcích jsou popsány místnosti. Na každém řádku je číslo uzlu a písmeno,
které udává, kdo v ní sedí:
-
P– v místnosti jsou programátoři -
M– v místnosti jsou manažeři -
E– místnost je prázdná
Formát výstupu: Vypište nejmenší počet uzávěrů, který Ondra musí přepnout, aby do místností tekl nebo netekl čaj (podle požadavků).
 Lehčí varianta (za 4 body): V lichých vstupech manažeři sídlí ve vedlejší
budově – v místnostech jsou buď programátoři, nebo tam není nikdo.
Lehčí varianta (za 4 body): V lichých vstupech manažeři sídlí ve vedlejší
budově – v místnostech jsou buď programátoři, nebo tam není nikdo.
8 4 1 2 O 1 3 Z 1 4 Z 2 5 O 3 6 O 4 7 O 4 8 Z 5 M 6 E 8 P 7 P
3
 35-3-2 Hroší hortenzie (10 bodů)
35-3-2 Hroší hortenzie (10 bodů)
 Lucce se na Internetu podařilo sehnat bylinný čaj Amacha
z fermentovaných listů hortenzie hroší (Hydrangea hippopotamina).
Tyto listy obsahují chemikálii zvanou hippopodulcin,
což je látka 400–800krát sladší než sacharóza.
Lucce se na Internetu podařilo sehnat bylinný čaj Amacha
z fermentovaných listů hortenzie hroší (Hydrangea hippopotamina).
Tyto listy obsahují chemikálii zvanou hippopodulcin,
což je látka 400–800krát sladší než sacharóza.
Lucka by ráda N svých kamarádů pohostila tímto sladkým čajem. O každém kamarádovi Lucka ví, jakou nejmenší a největší koncentraci hippopodulcinu (měřenou v mikrogramech na litr) by chtěl ve svém čaji mít. Zároveň ale chce spotřebovat co nejméně listů.
K přípravě čaje může Lucka využít některou z K mističek rozličných velikostí. Příprava čaje v i-té mističce probíhá tak, že se celá vystele listy hroší hortenzie, k čemuž je jich potřeba právě Li. Následně se až po okraj zalije 90stupňovou vodou, čímž po minutě vznikne čaj s koncentrací Ci mikrogramů hippopodulcinu na litr. Zde pro jednoduchost předpokládáme, že listy jsou stejně velké a každý z nich vylučuje stejné množství hippopodulcinu. Z listů lze takto připravit pouze jediný nálev.
Poraďte Lucce, ve které mističce má pro každého z kamarádů připravit jeden nálev čaje tak, aby vyhověla jejich nárokům, a přitom spotřebovala celkově co nejméně listů. Mističky se dají vymývat, takže dvěma různým kamarádům může Lucka připravit čaj ve stejné nádobě.
Všechny zadané hodnoty jsou nezáporná celá čísla, přičemž koncentrace hippopodulcinu mohou být velké až 109 μg/l. Můžete předpokládat, že kamarádů je řádově více než mističek.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 35-3-3 Prodlužovačky (12 bodů)
35-3-3 Prodlužovačky (12 bodů)
Kevina trápí problém. Rád si kutí a vytváří různé elektrické přístroje. Každý tento přístroj ale potřebuje být zapojený do elektřiny. Jelikož je ale Kevin nepořádný, vždy jen sáhne po nejbližší prodlužovačce, přístroj zapojí a kutí dál. Občas taky zapojí novou prodlužovačku, klidně i do jiné.
Nedávno ale zjistil, že každá prodlužovačka má určený maximální příkon, který snese. Aktuální příkon, kterému je prodlužovačka vystavena, jde určit jako součet příkonů připojených zařízení. Pro tyto potřeby se prodlužovačka, zapojená do jiné prodlužovačky, chová jako zařízení, jehož příkon se zjistí právě zmíněným způsobem.
Kevin si tedy zjistil pro každou prodlužovačku, jaký příkon snese, pro každé zařízení, jaký má příkon, a taky si udělal pořádek v tom, co je kam zapojené. Zjistil, že některé prodlužovačky jsou přetížené. Nyní by chtěl některá zařízení přepojit do zásuvek (těch má určitě dost a ty nemají omezený příkon) tak, aby žádná prodlužovačka přetížená nebyla. Prodlužek se momentálně bojí dotýkat, takže chce přepojovat pouze zařízení a nikoliv celé prodlužovačky. Jelikož se chce ale co nejdřív pustit znovu do kutění, chce přepojit co nejméně zařízení. Pomůžete mu?
Zmatek v Kevinově pokoji tvoří zakořeněný strom (tj. žádné zapojení prodlužovaček do sebe netvoří cyklus) a všechna zařízení jsou v listech tohoto stromu. Kořenem tohoto stromu je zeď, která má neomezený počet zásuvek. Pro každý list tohoto stromu (tj. pro každé zařízení) známe jeho příkon, což je kladné celé číslo. Pro každý vnitřní vrchol (tj. pro každou prodlužovačku) známe jeho kapacitu, což je nezáporné celé číslo určující maximální povolený součet příkonů listů v podstromu.
Navrhněte algoritmus, který pro zadanou soustavu prodlužovaček a zařízení vypíše, kolik nejméně a která zařízení odpojit z prodlužovaček a přepojit do zdi tak, aby nebyla pro žádnou prodlužovačku překročena kapacita.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 35-3-4 Záchrana listí (13 bodů)
35-3-4 Záchrana listí (13 bodů)
Honza se rozhodl založit si svou vlastní čajovnu. Vše potřebné už koupil a rozmístil. Protože místa měl málo, rozhodl se skladovat krabice s čaji na střeše své čajovny.
Aby se v krabicích s čajem dobře vyznal, tak je skladuje v řadě. Každá krabice obsahuje určité množství čaje. Kromě toho na některých krabicích jsou umístěná víka.
Honza šel na střechu sehnat čaj pro zákazníky, jenže ouha: Začalo pršet. Honza by samozřejmě chtěl zabránit tomu, aby jeho drahocenné listí zmoklo v krabicích. Všiml si, že do krabic s víkem neprší. Proto se rozhodl, že popřemisťuje víka tak, aby hmotnost suchého čaje byla co největší. Má to jeden háček: Víka jsou přivázaná, a dají se přemístit jen do omezené vzdálenosti. Honza ale nemá čas na složité plánování, jak víka přemístit (jinak mu čaj zmokne), proto se ptá, jestli mu pomůžete.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku najdete dvě čísla N a K – počet krabic a délku provázku.
Na dalších N řádcích dostanete dvě čísla mi a vi, popisující i-tou krabici.
Číslo mi udává hmotnost čaje v ní a vi, zdali má na sobě víko (1 pokud má, jinak 0).
Hodnota délky provázku určuje, o kolik krabic vedle se dá víko přesunout. Např. K = 1 znamená, že víko se dá nejdále posunout na krabice hned vedle.
Formát výstupu: Na první řádek vypište největší možné množství čaje, které má šanci Honza zachránit. Poté vypište pro každé víko index původní krabice, ke které je přivázané, a číslo krabice, na které je teď položené.
 Lehčí varianta (za 7 bodů):
Slibujeme, že v prvních čtyřech vstupech se dají víka přesunout nejdále na sousední krabice.
Je tam tedy tedy K = 1.
Lehčí varianta (za 7 bodů):
Slibujeme, že v prvních čtyřech vstupech se dají víka přesunout nejdále na sousední krabice.
Je tam tedy tedy K = 1.
6 2 1 1 2 0 4 1 0 0 5 0 3 1
12 3 5 6 6 1 3
 35-3-X1 Obvody (10 bodů)
35-3-X1 Obvody (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
Jirka se snažil spravit Danovu rozbitou myšku. Proto si navrhl obvod se spoustou součástek. Chystal se obvod spájet a podíval se tedy do svého šuplíku na součástky, jenže zjistil, že mu došly veškeré rezistory.
Proto Jirka vyhrabal svoji zásobu součástek do největší krize. Tam má pro každou kladnou celočíselnou hodnotu odporu právě jeden rezistor. Ví, že do i-tého místa v obvodu potřebuje právě jeden rezistor, který může mít hodnotu odporu v jednom z Mi intervalů:
kde ℓ1 ≤ r1 < ℓ2 ≤ r2 < … a každé ℓj, rj ∈ Z+.
Po vás by chtěl každému místu na obvodu přiřadit jeden rezistor, který má odpor v jednom z pro něj povolených intervalů. Bohužel pro každou hodnotu odporu má rezistor pouze jeden.
Např. pro místa v obvodu s povolenými rozsahy:
je jedno z možných přiřazení 2, 1, 4, 3, 5.
| N |
| i=1 |
 35-3-S Vektorové prostory (15 bodů)
35-3-S Vektorové prostory (15 bodů)
Právě čtete třetí díl seriálu. Pokud jste předchozí díly neřešili, pro pochopení následujících odstavců je vhodné si je přinejmenším přečíst. Navíc je stále možné odevzdávat úlohy z nich za polovinu bodů.
V tomto dílu se vrátíme k již známým pojmům, jen se na ně tentokráte podíváme o trochu obecněji.
Všechny úlohy z tohoto dílu odevzdávejte dohromady v jednom zazipovaném archivu. První termín odevzdání je shodný s termínem pro třetí sérii. Poté lze odevzdávat za snížený počet bodů až do konce ročníku.
Souřadnice
Ve druhém dílu jsme zavedli pojem báze. Pro připomenutí, báze prostoru U je soubor vektorů z U, které tento prostor generují a zároveň jsou lineárně nezávislé. Také jsme potkali kanonickou bázi, tedy bázi prostoru Rd složenou z jednotkových vektorů.
S kanonickou bází se dobře pracuje, neboť souřadnice vektorů standardně píšeme vzhledem k ní. Můžeme je však psát i vzhledem k jiné bázi B = b1,…,bn. Vezměme si nějaký vektor v a zapišme jej jako lineární kombinaci:
| n |
| i=1 |
Poté jako souřadnice vektoru v vzhledem k bázi B nazveme koeficienty a1,…,an. Matematicky zapisujeme [v]B = (a1,…,an)⊤.
Ukažme si na příkladu. Vektor v = (5,2)⊤ má souřadnice vzhledem ke kanonické bázi [v]kan = (5,2)⊤. Jeho souřadnice vzhledem k bázi B = (1,4)⊤, (-2,1)⊤ jsou [v]B = (1,-2)⊤.
Povšimněte si, že potřebujeme obě vlastnosti báze, aby byly souřadnice jednoznačné. Kdyby bazické vektory negenerovaly prostor, některé vektory z něj by neměly souřadnicové vyjádření. Kdyby byly lineárně závislé, jeden vektor by mohl mít více souřadnic.
Souřadnice jsme již počítali dříve, byť jsme jim samozřejmě neříkali takto, například v úloze Robot na Marsu. Připomeňte si, jak výpočet probíhal.
Od té doby se však naše znalosti rozšířily. Nyní můžeme na výpočet souřadnic pohlížet také jako na zobrazení, které vektory báze B zobrazí na vektory kanonické báze. Neboť je toto zobrazení lineární, platí linearita i pro souřadnice:
Ještě se nám bude hodit jedno pozorování, totiž že všechny báze prostoru U mají stejný počet vektorů. Již v prvním dílu jsme nahlédli, že mezi lineárně závislými vektory jsou některé nadbytečné, i po jejich odebrání budou ty zbylé generovat stejný prostor. Obecně platí (byť to nebudeme dokazovat), že počet generátorů prostoru U bude vždy větší nebo roven počtu lineárně nezávislých vektorů v U. Máme-li dvě báze B1 a B2, můžeme tento fakt použít v obou směrech. Nejprve budeme B1 považovat za generátory a B2 za nezávislý soubor, čímž dostaneme nerovnost |B1| ≥ |B2|. Prohozením získáme opačnou nerovnost, spojením obou nerovností kýženou rovnost.
Jelikož jsou všechny báze prostoru stejně veliké, můžeme definovat dimenzi prostoru jako velikost libovolné z bází.
Obecné prostory
Souřadnice nám nyní umožní zobecnit myšlenku vektorových prostorů. Dosud to pro nás byl pouze pojem popisující množiny Rd, takzvané aritmetické prostory. Pomocí souřadnic budeme schopni převést na aritmetické prostory i jiné množiny.
Tuto myšlenku si ukažme na již známém lineárním obalu. Zvolme dva trojrozměrné vektory, například u1 = (2, 2, 2)⊤, u2 = (3, 4, 5)⊤, a zaveďme lineární obal U = span{u1, u2}. Množina U má podobu roviny, nejedná se však o prostor R2 (třeba u1 v R2 neleží). Přesto s ním úzce souvisí.
Daná souvislost vynikne, pokud prostor U popíšeme pomocí báze B = u1, u2. Souřadnice jakéhokoli vektoru z U vzhledem k bázi B mají podobu dvourozměrného vektoru, tedy vektoru z R2. Dokud tedy pracujeme se souřadnicemi, oba prostory jsou totožné; rozdíl tkví pouze v použité bázi. Poznatky, které jsme získali pro aritmetické prostory, můžeme převést do obecných prostorů:
- Chceme-li ověřit nezávislost vektorů x, y∈U, stačí ověřit nezávislost jejich souřadnic [x]B, [y]B.
- Obdobně, chceme-li vyjádřit vektor v∈U jako lineární kombinaci jiných vektorů, stačí najít koeficienty, které vyjádří [v]B pomocí souřadnic daných vektorů.
Zmíněná tvrzení platí díky linearitě souřadnic.
Prostory funkcí
Proč se však omezovat na prostory aritmetických vektorů? Když už umíme reprezentovat prostory pomocí souřadnic, můžeme si dovolit exotičtější prostory.
Vektorovým prostorem může být například množina Q kvadratických funkcí q(x) = ax2 + bx + c. Slovo vektor se v kontextu prostorů používá jako obecný termín pro jednotlivé prvky množiny, v tomto případě pro konkrétní funkce. Jeden možný vektor by tedy byl q1(x) = 3x2 + 5. Po vektorech chceme, abychom je mezi sebou mohli sčítat a násobit skalárem, což kvadratické funkce splňují – sečteme odpovídající koeficienty, případně je všechny vynásobíme příslušným skalárem. Aby se jednalo o vektorový prostor, ještě musí být splněno pár dalších podmínek, jak si ukážeme za chvíli.
Jedna možná báze tohoto prostoru je B = 1, x, x2. Souřadnicemi vektoru by byly jednoduše koeficienty (c, b, a)⊤.
Pro různá použití se však hodí různé báze. Mohlo by být výhodnější reprezentovat funkce pomocí jejich funkčních hodnot v bodech x = -1, 0, 1 (tři body určují kvadratickou funkci jednoznačně). Hledáme tedy bázi C = c1, c2, c3 , aby souřadnice vzhledem k C byly [q]C = (q(-1), q(0), q(1))⊤.
Jak takovou bázi najít? Inu, musí platit [c1]C = (1, 0, 0)⊤. Dostáváme soustavu tří rovnic pro neznámé a, b, c:
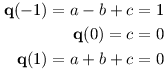
Řešení je a = 1/2, b = -1/2, c = 0, takže c1 = 1/2 x2 - 1/2 x. Obdobně pro c2 a c3.
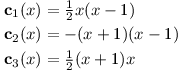
 Tuto myšlenku lze rozšířit. Máme n+1 bodů v rovině (xi, yi)
a hledáme polynom n-tého stupně, který těmito body prochází.
Řešení nabízí Lagrangeův interpolanční polynom.
Zvolíme bázi L = p0, …, pn, kde
Tuto myšlenku lze rozšířit. Máme n+1 bodů v rovině (xi, yi)
a hledáme polynom n-tého stupně, který těmito body prochází.
Řešení nabízí Lagrangeův interpolanční polynom.
Zvolíme bázi L = p0, …, pn, kde
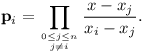
Jedná se o stejné polynomy, jaké jsme dostali pro kvadratické funkce. Po polynomu pi chceme, aby měl v bodě xi hodnotu 1, v ostatních xj hodnotu 0. Nulové hodnoty zajistíme výrazem x - xj, který navíc vhodně přenásobíme, aby byl celý výraz v bodě xi roven 1. Polynom se souřadnicemi (y0, …, yn)⊤ vzhledem k bázi L tedy prochází všemi body. Převedením do báze 1, x, …, xn získáme jeho koeficienty.
Síla abstrakce
Prostor funkcí nebyl dosti exotický? Tak co množina smějících se a mračících se hrochů?

Dokonce i to může být vektorový prostor, jen bychom museli zadefinovat, jak se bude chovat sčítání hrochů a jejich násobení skalárem. Nejspíše bychom chtěli sčítat jejich nálady, přičtením smějícího se hrocha by se úsměv zvětšil, přičtením mračícího se hrocha zase zmenšil. Nepůjde využít standardní sčítání a násobení, vždyť se nejedná o čísla, museli bychom si tak vymyslet vlastní operace. Jak se dozvíme za chvíli, tyto operace však musí splňovat určitá pravidla.
Pomalu přichází čas uvést si přesnou definici vektorového prostoru. Co vlastně od takové definice očekáváme? Na jednu stranu bychom chtěli, aby pro každý vektorový prostor platily poznatky, které jsme učinili o aritmetických prostorech. Na druhou stranu bychom rádi umožnili, aby si každý mohl vymyslet svůj vlastní vektorový prostor, s vlastním sčítáním a násobením, třeba smějící se hrochy.
Nemůžeme tedy popsat vektorový prostor přímo. Místo toho ponecháme definici plně abstraktní, pouze vyjmenujeme vlastnosti, které musí splňovat. Tyto vlastnosti se nazývají axiomy a jsou to jediné, z čeho můžeme chování vektorových prostorů odvozovat.
 Pro vyřešení úloh není nutné axiomy znát, ba ani pochopit.
Dají vám však malý náhled do světa matematiky za hranicí středoškolského učiva.
Pro vyřešení úloh není nutné axiomy znát, ba ani pochopit.
Dají vám však malý náhled do světa matematiky za hranicí středoškolského učiva.
Vektorový prostor je množina V, kde platí:
- Asociativita sčítání: x + (y + z) = (x + y) + z
- Komutativita sčítání: x + y = y + x
- Existence nuly: ∃0 ∀x: 0 + x = x + 0 = x
- Existence opačného prvku: ∀x ∃x': x + x' = x' + x = 0
- Asociativita násobení: a(bx) = (ab)x
- Existence jedničky: 1x = x
- Distributivita poprvé: a(x + y) = ax + ay
- Distributivita podruhé: (a + b)x = ax + bx
Není-li uvedeno jinak, dané vlastnosti musí platit pro všechny vektory x, y, z∈V a všechny skaláry a, b.
Standardní sčítání a násobení všechny tyto axiomy splňuje. V prostoru hrochů by například pravidlo 3 znamenalo, že musí existovat hroch s neutrálním výrazem, který se ani nesměje, ani nemračí, a jeho přičtení k jinému hrochovi nezpůsobí žádnou změnu. Pravidlo 4 říká, že hrochy lze rozdělit do dvojic s opačnou náladou, jen chudák neutrální hroch bude ve dvojici sám se sebou. Poslední 4 pravidla předurčují, že násobení se musí chovat jako opakované sčítání. Například z pravidel 8 a 6 vyplývá:
Aby toho nebylo málo, lze přidat ještě jedno zobecnění. Místo skalárů z R můžeme vektorový prostor definovat nad jakýmkoli tělesem, například nad Q nebo nad C. (Pozor, obory N a Z tělesa nejsou!) V informatice se hodí těleso Z2, které má prvky 0 a 1 a sčítání se tam chová jako binární xor.
Zobrazení mezi prostory
Zobrazení jsme doteď vnímali jako transformace obrázků, tedy transformace v Rd. Nic však nebrání tomu, aby zobrazení jako vstup dostalo vektor z prostoru U a jako výstup vydalo vektor z prostoru V. Říkáme, že zobrazení f je z U do V, matematicky f:U→V.
Menší zádrhel přijde ve chvíli, kdy budeme chtít zobrazení popsat maticí. Jak jsme odvodili v minulém dílu, ve sloupcích matice jsou obrazy jednotkových vektorů. Jednotkových proto, že jsme pracovali v kanonické bázi. Dokonce i obrazy samotné jsme zapsali vzhledem k ní. Jenže v obecných prostorech žádná kanonická báze existovat nemusí.
Musíme si tedy vybrat bázi, kterou bude matice používat. A to hned dvě, jednu pro prostor U a jednu pro prostor V. Matice tak vlastně bude zobrazení popisovat v řeči souřadnic. Pro bázi BU prostoru U a bázi BV prostoru V budeme matici zobrazení f značit BV[f]BU.
Ukažme si příklad na prostoru kvadratických funkcí Q zavedeném výše. Nejprve uvážíme zobrazení f:Q→R, které vyhodnotí funkci v bodě x=3. Prostor Q má dimenzi 3, prostor R dimenzi 1, matice tak bude mít rozměry 3×1. Použijeme-li bázi B = 1, x, x2, dostaneme matici:
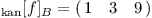
A obraz vektoru q1(x) = 3x2 + 5 vypočteme následovně:
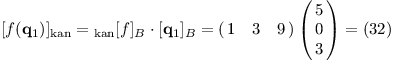
Povšimněte si, že v dolních indexech jsou stejné báze u sebe, jedině tak jsou vektory s maticí kompatibilní.
Jako druhý příklad použijeme zobrazení g:Q →Q, které funkci zrdcadlově převrátí podél osy y. To bude naopak jednodušší v bázi C, pouze se prohodí funkční hodnoty v bodech x=-1 a x=1:
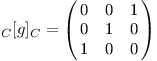
Přechod mezi bázemi
Matice výše pracuje s bází C. Pokud bychom měli vektor v bázi B, museli bychom jej přeložit. Matice, která to zajistí, se nazývá matice přechodu a značí se C[id]B. Ve značení využíváme identitu – zobrazení, které nic nemění. Podobu této matice jsme již naznačili v sekci o souřadnicích, v jejích sloupcích budou vektory báze B zapsané v bázi C.
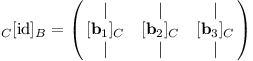
Složením zobrazení dokonce zvládneme spočítat matici zobrazení g, která pracuje rovnou v bázi B:
Úkol 1 – Matice přechodu [7b]
Sestavte obě matice přechodu, z báze B do C (popsaných výše) a zpět. Poté pomocí nich spočítejte B[g]B. Popište, jak by ji šlo přímo odvodit interpretací zobrazení g, podobně jako jsme odvodili C[g]C.
Maticové prostory
Hezké vektorové prostory vychází z matic. Pro A∈Rm×n definujeme sloupcový prostor S(A) jako lineární obal sloupců matice, tedy span{ (A)*1, …, (A)*n }. Pokud maticí A popíšeme zobrazení, pak sloupcový prostor odpovídá oboru hodnot. Proč tomu tak je? Obor hodnot je množina výrazů Ax pro všechny x∈Rn. Složky vektoru x se při násobení s maticí chovají jako koeficienty, kterými se násobí sloupce A, vytváří se tedy jejich lineární kombinace.
Podobným způsobem zavedeme řádkový prostor R(A) jako lineární obal řádků, tedy span{ (A)1*, …, (A)m* }. Jeho význam nahlédneme zanedlouho.
Posledním prostorem je množina všech x∈Rn, pro která platí Ax = 0. Tento prostor je nazývá jádro matice a značí se ker(A). Zde již nemusí být na první pohled zřejmé, že se jedná o vektorový prostor. Jedná se o podmnožinu prostoru Rn, což zajistí většinu vlastností, které od prostoru požadujeme. Ještě je potřeba ukázat, že tato podmnožina je neprázdná a že je uzavřená na součet a násobek skalárem. Přinejmenším platí 0∈ker(A), protože součin A0 určitě bude roven nule. Pokud x, y∈ker(A), poté jejich pro jejich součet platí A(x + y) = Ax + Ay = 0 + 0 = 0, ten tedy v jádru leží. Pro násobek skalárem obdobně.
Jádro má taktéž význam ve spojitosti s lineárními zobrazeními. Jádro obsahuje jen a pouze nulový vektor právě tehdy, když je zobrazení prosté, tedy když se žádné dva vektory nezobrazí na stejný obraz. Nahlédněme odůvodnění alespoň implikace zprava doleva: Pro každé lineární zobrazení platí f(0) = 0 a prosté zobrazení již žádný další prvek na 0 zobrazit nemůže.
Bez důkazu uvedeme následující větu (dim V značí dimenzi vektorového prostoru V):
Co nám věta říká? Uvažme výraz Ax, kde x∈Rn. Pokusme se sestavit nějakou bázi prostoru Rn. Za část bazických vektorů, konkrétně za k = dim ker(A) z nich, můžeme zvolit bazické vektory jádra. Ještě potřebujeme dalších n - k, dle věty výše je tento počet roven r = dim R(A). Bázi tedy doplníme bazickými vektory řádkového prostoru. Poznamenejme, že takové doplnění neporuší lineární nezávislost a tudíž jej lze provést, odůvodnění uvidíme ve čtvrtém dílu.
V důsledku lze každý vektor x∈Rn jednoznačně rozložit jako x = xR + xK, kde xR ∈ R(A) a xK ∈ ker(A).
Navíc, díky shodné dimenzi řádkového a sloupcového prostoru existuje mezi vektory těchto prostorů párování neboli bijekce. V rovnici AxR = b tedy pro každé xR existuje jediné b a naopak.
Úkol 2 – Soustavy pomocí maticových prostorů [5b]
Pro danou matici A∈Rm×n známe S(A), R(A), ker(A). Všechny máme reprezentované pomocí jejich bází:
- Báze S(A) sestává z r vektorů s1, …, sr,
- báze R(A) sestává z r vektorů r1, …, rr,
- báze ker(A) sestává z k vektorů k1, …, kk.
- Rozhodněte, kolik řešení má soustava Ax = b.
- Znáte-li jedno řešení x0, vyjádřete množinu všech řešení.
Porovnejte časovou složitost vašeho přístupu s přímočarým hledáním všech řešení pomocí Gaussovy eliminace. Ve kterých případech je váš přístup výhodnější?
Prostory posloupností
Na závěr se podívejme na posloupnosti zadané rekurentním vztahem. V jedné z úloh minulého dílu jsme zjistili, jak rychle spočítat člen Fibonacciho posloupnosti. Pomocí vektorových prostorů dokážeme pro podobné posloupnosti odvodit explicitní vzorec.
Uvažme posloupnost (s0, s1, s2, … ) zadanou rekurentním vztahem sn+2 = 2sn+1 + 3sn. Takových posloupností je více, označme jejich množinu S. Když bychom určili první členy s0, s1, získali bychom konkrétní posloupnost. Množina S tvoří vektorový prostor, sčítáme a násobíme po členech. Podobně jako dříve, použitím standardního sčítání a násobení splníme většinu axiomů. Nulová posloupnost do prostoru patří, uzavřenost na operace také platí.
Konkrétní posloupnost je určena dvěma prvními členy, prostor S má tedy dimenzi 2. Pokusme se najít jeho bázi. Rekurentní posloupnosti většinou rostou exponenciálně, zkusme tedy zjistit, jestli není exponenciální posloupnost αn součástí prostoru S pro vhodné α. Pro tuto posloupnost platí sn+1 = αsn, což dosadíme do rekurentního vztahu:
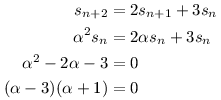
Našli jsme dva bazické vektory: b1 = 3n, b2 = (-1)n. Každá posloupnost prostoru S jde vyjádřit jako jejich lineární kombinace.
Úkol 3 – Rekurence [3b]
Najděte explicitní vzorec pro člen sn posloupnosti zadané rekurentním vztahem výše a prvními členy s0 = 0, s1 = 1, tedy 0, 1, 2, 7, 20, 61, 182, 547, …