První série třicátého pátého ročníku KSP
Celý leták v PDF.
Dostává se k vám první číslo hlavní kategorie 35. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Také na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: 30. října 2022 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo z každé úlohy série získá alespoň 2 body.
Zadání úloh
- 35-1-1: Hroší přeslička
- 35-1-2: Vaření lektvarů
- 35-1-3: Letadélko
- 35-1-4: Atlas zlomků
- 35-1-S: Lineární rovnice
- 35-1-X1: Rejstřík zlomků
 35-1-1 Hroší přeslička (9 bodů)
35-1-1 Hroší přeslička (9 bodů)
Petr se vypravil do hor pátrat po stopách bájné hroší přesličky (Hippochaete montana). Říká se, že odvar z ní rozjasní mysl a pomůže nejenom při řešení úložek v KSP. Najít ji ale vůbec není jednoduché.

Horu si lze představit jako množinu N křižovatek a N-1 cestiček, přičemž každá cestička spojuje dvě křižovatky. Na horách se dá bezpečně pohybovat jedině po cestičkách a křižovatkách. Navíc platí, že mezi libovolnými dvěma křižovatkami lze přecházet pouze jedním způsobem (formálně řečeno se jedná o strom). Vypadat může třeba takto:
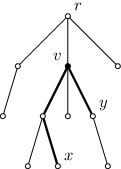
Křižovatka r odpovídá vrcholu hory (je nejvýš), křižovatka v je níž, y ještě níž a tak dále. Obecně jdeme-li z nějaké křižovatky směrem k r, pohybujeme se nahoru, jinak dolů.
Trasa budeme říkat procházce z jedné křižovatky na jinou, která nenavštíví žádnou křižovatku vícekrát. Každá trasa má jediný nejvyšší bod – křižovatku nejbližší vrcholu hory. Na obrázku jsme tučně nakreslili trasu z x do y, jejím nejvyšším bodem je v. Trasa z x do v má nejvyšší bod v.
Teď uvážíme všechny možné trasy. Jelikož každá trasa je jednoznačně určena svou první a poslední křižovatkou, existuje právě N·(N-1) různých tras.
Legenda praví, že hroší přeslička roste pouze na takovém místě, které se nejčastěji vyskytuje jako nejvyšší bod trasy.
Na našem obrázku je například křižovatka v nejvyšším bodem 34 tras. (6 tras vede zespodu do v, dalších 6 z v dolů, 22 tras má začátek i konec někde pod v). Ale ještě častěji se vyskytuje křižovatka r – je nejvyšším bodem 66 tras.
Petr se rozhodl, že přesličku najde. V atlase si proto našel mapu hory s vyznačenými cestičkami. Pomůžete mu určit, kam by se měl vypravit, aby hroší přesličku zaručeně získal?
Vaším úkolem je vymyslet a sepsat algoritmus, který na vstupu dostane popis terénu hory a na výstupu vrátí identifikátor křižovatky, na které podle legendy roste hroší přeslička. Pokud takových míst existuje více, nechť vypíše libovolné z nich.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
Můžete předpokládat, že každá křižovatka má unikátní celočíselný identifikátor
z rozmezí od 1 do N. Vrchol hory se nachází na křižovatce číslo 1.
Samotný terén je následně popsaný pomocí N-1 cestiček ve tvaru U V, kde
U a V jsou křižovatky na okrajích cestičky a zároveň U se nachází
nad V.
 35-1-2 Vaření lektvarů (10 bodů)
35-1-2 Vaření lektvarů (10 bodů)
Aspirující alchymista Demivirtos dostal zakázku na dodání sady lektvarů. Jelikož se snaží vybudovat si dobrou pověst, chce ji splnit co nejrychleji. Ve svojí nově rozšířené laboratoři dokáže vařit prakticky neomezené množství lektvarů zároveň, problém však je, že složitější lektvary používají jako ingredience ty jednodušší. Může je tedy začít připravovat, až když jsou dovařené všechny jejich prerekvizity. Jakmile však už jeden lektvar dodělá, má ho neomezené množství, takže ho může použít na výrobu dalších lektvarů, a dokonce mu zbude.

Spočítejte, kdy může Demivirtos začít připravovat jednotlivé lektvary, aby měl zakázku připravenou co nejdříve. Zakázka je připravená, když jsou hotové všechny lektvary.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete čísla N – počet různých lektvarů a M – počet závislostí.
Na druhém řádku dostanete N čísel Si říkající, jak dlouho trvá připravit i-tý lektvar.
Na každém ze zbylých M řádků je pak dvojice čísel Pj a Qj. Každá říká, že Qj-tý lektvar se může začít připravovat až po dokončení Pj-tého. Lektvary jsou číslovány od 1 do N.
Máte zaručeno, že postup, jak lektvary uvařit, skutečně existuje – nestane se tedy, že dva nebo více lektvarů bude čekat vzájemně na sebe.
Formát výstupu: Vypište jeden řádek s N čísly Si říkající, kdy se má začít připravovat i-tý lektvar.
 Lehčí varianta (za 4 body):
Slibujeme, že v prvních dvou vstupech bude každý lektvar vyžadovat maximálně jeden jiný.
Lehčí varianta (za 4 body):
Slibujeme, že v prvních dvou vstupech bude každý lektvar vyžadovat maximálně jeden jiný.
5 3 2 2 3 4 1 3 4 1 2 2 4
0 2 1 4 6
Zakázka bude připravená v čase 8, kdy se dokončí čtvrtý lektvar, který potřebuje první tři. Pátý lektvar, který nic nepotřebuje, se může vařit kdykoliv mezitím.
 35-1-3 Letadélko (12 bodů)
35-1-3 Letadélko (12 bodů)
Kevin se Sárou byli o prázdninách v Řecku. A protože Kevin už měl koupání u moře dost, rozhodl se, že vyzkouší svůj model letadélka.
Kevin svoje letadélko pustil z pláže na úrovni mořské hladiny a nasměroval ho k Sáře, která čekala na druhém ostrově. Letadélko se začalo pohybovat vpřed, kromě toho dělalo i pohyby nahoru a dolů. Na konci slétlo zpět na úroveň mořské hladiny, aby ho Sára mohla chytit. Letadélko ale není voděodolné, takže nikdy nemohlo klesnout pod úroveň mořské hladiny.
Kevin se chtěl následně podívat na záznam letové výšky, bohužel ale zjistil, že slaný mořský vzduch letadélku nesvědčí a některé části záznamu jsou vymazané. Vzhledem k tomu, že poškozených částí je velmi málo, Kevin si myslí, že by mohl projít všechny možnosti, jak mohlo letadlo letět, a z toho, co si pamatuje, najít tu správnou. Řekněte mu, kolik možností je, aby tušil, jak dlouho mu to bude trvat.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostatne číslo N – délku záznamu.
Na druhém řádku dostanete záznam složený ze tří symbolů: ^ znamená, že letadlo letělo o 1 metr nahoru, v znamená, že letadlo letělo o 1 metr dolů. ? znamená, že záznam je zde poškozený a letadlo mohlo letět o 1 metr dolů nebo nahoru.
Slibujeme, že počet poškozených částí je velmi malý.
Formát výstupu: Vypište jedno číslo – počet možností, jak lze otazníky nahradit ^ nebo v, aby let letadélka splňoval dvě podmínky:
- Letadélko startovalo ve výšce 0 a skončilo ve výšce 0.
- Letadélko nikdy nekleslo pod mořskou hladinu.
Počet možností může být opravdu velký, a proto bude v některých jazycích zapotřebí použít 64-bitového datového typu (v C++ je to long long int).
Pokud programujete v Pythonu, pak toto řešit nemusíte.
4 ^??v
2
Existují dvě různé možnosti letu: ^^vv a ^v^v.
 35-1-4 Atlas zlomků (14 bodů)
35-1-4 Atlas zlomků (14 bodů)
Velký detektiv K. S. Pinkerton luští tajnou zprávu, ve které jsou slova zašifrovaná do zlomků. Všiml si, že všechny zlomky ve zprávě jsou v základním tvaru (nedají se zkrátit), leží mezi 0 a 1 (včetně) a jejich čitatelé i jmenovatelé jsou v rozsahu 1 až N. Hodil by se mu seznam všech takových zlomků.
Navrhněte algoritmus, který pro zadané N vypíše všechny zlomky uvedených vlastností. Pokuste se o co nejlepší časovou složitost vzhledem k počtu vypsaných zlomků. Zlomky můžete vypsat v libovolném pořadí, ale každý by se měl objevit právě jednou.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
Příklad: Pro N=5 to jsou zlomky 1/1, 1/2, 1/3, 1/4, 1/5, 2/3, 2/5, 3/4, 3/5, 4/5.
 35-1-X1 Rejstřík zlomků (10 bodů)
35-1-X1 Rejstřík zlomků (10 bodů)
Podobně jako v úloze 35-1-4, i zde budeme hledat zlomky v základním tvaru mezi 0 a 1, jejichž čitatel i jmenovatel jsou v rozsahu 1 až N. Vypište nejmenších K takových zlomků uspořádaných vzestupně. Slibujeme, že K ≥ N.
Příklad: Pro N=5 a K=6 máte vypsat seznam 1/5, 1/4, 1/3, 2/5, 1/2, 3/5.
 35-1-S Lineární rovnice (15 bodů)
35-1-S Lineární rovnice (15 bodů)
Letošním ročníkem vás bude provázet seriál. V každé sérii se objeví jeden díl, který bude obsahovat nějaké povídání a navíc úkoly. Za úkoly budete moci získávat body podobně jako za klasické úlohy série. Abyste se mohli zapojit i během ročníku, seriál bude možné odevzdávat i po termínu za snížený počet bodů. Vzorové řešení seriálu proto před koncem celého ročníku KSP uvidí jen ti, kdo už seriál odevzdali.
V letošním seriálu se ponoříme do světa lineární algebry, do světa vektorů a matic, které elegantně popisují geometrické objekty a operace s nimi. Lineární algebra vládne vědeckým výpočtům, a to i v oblastech, které s geometrií nemají téměř nic společného. Nabídne nám algoritmy na problémy, které se jinak řeší těžko, a mnoho dalších algoritmů pomocí jejích triků dokážeme zefektivnit. Vstupenku do tohoto světa naleznete v následujících odstavcích.
Vektory
Aritmetický vektor není nic jiného než seznam čísel. Těmto číslům říkáme složky vektoru. Může jich být libovolný počet d, pak vektoru říkáme d-rozměrný neboli d-dimenzionální. Trojrozměrný vektor může vypadat třeba takhle:
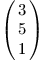
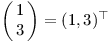
Vektory si lze představit jako body v d-dimenzionálním prostoru. Nejčastěji se budeme setkávat se dvoudimenzionálními vektory, které si představíme jako body v rovině: jejich složky udávají souřadnice bodu. Běžné jsou také třídimenzionální vektory reprezentující body v prostoru. Vektor si také můžeme vyložit jako posunutí z počátku souřadnic do zmíněného bodu. Vektor, který leží v počátku a nikam nevede (takže všechny jeho složky jsou nulové) se nazývá nulový vektor a budeme jej značit 0.
Prostým reálným číslům se (pro lepší odlišení od vektorů) říká skaláry. Abychom odlišení dosáhli i v matematice, budeme vektory psát tučně: x. Jednodimenzionální vektor má jedinou složku a lze jej tedy považovat jak za vektor, tak za skalár.
Vektory stejných rozměrů můžeme sčítat jednoduše sečtením po složkách. Stejně tak vynásobení vektoru skalárem bude znamenat prosté vynásobení každé ze složek. Této operaci budeme také říkat škálování. To zní podobně jako skalár, náhoda?
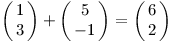
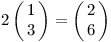
Lineární kombinace
Množina všech vektorů Rd má hezkou vlastnost: Součet dvou vektorů z této množiny opět leží v této množině. Totéž platí pro vynásobení vektoru reálným skalárem. Pokuste se odůvodnit, proč tomu tak je. Jelikož tato vlastnost vyvstává v matematice poměrně často, má své vlastní jméno: Říkáme, že množina Rd je uzavřená na operace sčítání a násobení skalárem. Množině, která je uzavřená na tyto dvě operace (a kde je sčítání a násobení definované „rozumně“), se říká vektorový prostor. S vektorovými prostory se blíže seznámíme ve třetím dílu.
Vektorový prostor můžeme popsat pomocí souřadnic. Nejprve zavedeme jednotkové vektory, které obsahují samé nuly a jednu jedničku. Například ve trojrozměrném prostoru to jsou (1, 0, 0)⊤, (0, 1, 0)⊤ a (0, 0, 1)⊤. Pomocí jednotkových vektorů pak můžeme zapsat libovolný vektor:
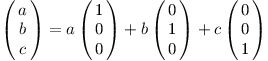
Možná jste na střední škole potkali analytickou geometrii, která popisuje rovinu pomocí kartézské soustavy souřadnic. Totéž jde říci pomocí lineární algebry: rovina odpovídá vektorovému prostoru R2, souřadné osy mají stejný směr jako jednotkové vektory a konkrétní souřadnice bodu odpovídají složkám vektoru.
Lineární kombinace umí pracovat i s jinými vektory než jednotkovými. Obecně nám umožňuje vzít několik libovolných vektorů, ze kterých poskládáme nový vektor tím, že je přeškálujeme a poté sečteme. Zapsáno matematicky, lineární kombinace v vektorů x1,…,xn je následující výraz pro libovolné hodnoty koeficientů a1,…,an:
| n |
| i=1 |
Pokud jste se ještě nesetkali se sumou (∑), výraz výše znamená: Pro všechny hodnoty i od 1 do n, vezmi výraz ai xi a všechny tyto výrazy sečti. Po rozepsání bychom tedy dostali:
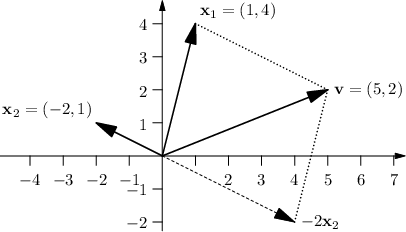
Co to celé vlastně znamená? Dejme tomu, že se v prostoru umíme pohybovat pouze některými směry, x1,…,xn, a chceme se dostat do bodu určeného vektorem v. Pokud najdeme vhodné koeficienty, pro které je v lineární kombinací směrů pohybu, zjistíme, jak daleko musíme v každém z těchto směrů ujít, abychom se do daného bodu dostali.
Následující obrázek ilustruje lineární kombinaci
Úkol 1 – Robot na Marsu [5b]
Vesmírná sonda Hipporover přistává na Marsu. Po přistání se má vydat směrem k nejbližšímu kráteru. Sonda má dvě sady koleček, jedny jí umožní jet dopředu, jedny do strany. Pro účely navigace nahráli výzkumníci do sondy mapu povrchu Marsu v kartézském souřadnicovém systému a naprogramovali přesnou posloupnost pohybů, jaké sonda musí vykonat, aby se ke kráteru dostala.
Každý pohyb má udaný směr (dopředu, doleva) a vzdálenost, jakou má sonda v tomto směru ujet. Tato vzdálenost může být záporná, poté jede sonda opačným směrem. Pohyb dopředu o jeden metr odpovídá vektoru (1, 0)⊤, pohyb doleva vektoru (0, 1)⊤.
Ale ouha, sonda měla potíže při přistání a některé součástky se zkratovaly. Teď jde do nějakých koleček více napětí, než by mělo, a sonda nejezdí rovně, dokonce ani směry jejich pohybů již na sebe nejsou kolmé.
Naštěstí má sonda kalibrační systém a dokáže zjistit vektory svých pohybů vůči kartézské soustavě souřadnic. Skvělé, ale jak nyní opravit plán a dostat vozítko do cílového místa? Výzkumníci si s tím nevědí rady. Pomozte jim!
Dostanete dva dvourozměrné vektory. První popisuje, jak se sonda pohne, pokud dostane povel popojet o jeden metr dopředu. Druhý popisuje totéž pro povel doleva. Můžete předpokládat, že tyto vektory jsou nenulové a mají různý směr.
Popište, jak simulovat původní povely pomocí nových pohybů. Tedy jaké pohyby má sonda provést pro povel „popojeď dopředu o m metrů“ a jaké pro povel „doleva o m metrů“.
Lineární obal
Mohlo by nás také zajímat, do jakých všech bodů se lze pomocí pohybů x1,…,xn dostat. To tedy bude množina všech lineárních kombinací těchto vektorů pro všechny možné hodnoty koeficientů. Tato množina se nazývá lineární obal a vektory x1,…,xn se v tomto kontextu nazývají generátory.
Funkce, která počítá lineární obal, se značí span. Tato funkce má jeden argument, konkrétně množinu generátorů. Lineární obal proto budeme značit span{x1,…,xn}.
Jak lineární obal vypadá? Pokud se nemůžeme pohybovat žádným směrem, zůstaneme v počátku, lineární obal je tedy jediný bod. Můžeme-li se pohybovat jedním směrem, množina všech dosažitelných bodů má podobu přímky procházející počátkem. Přidáním druhého generátoru lze vyrobit z přímky rovinu, přidáním třetího trojrozměrný prostor.
Lineární obal je uzavřený na lineární kombinace stejně jako celý vektorový prostor Rd. (Nevěříte? Zkuste to dokázat, není to těžké.) Je tedy taktéž vektorovým prostorem. Protože je zároveň podmnožinou prostoru Rd, říká se mu podprostor.
Lineární závislost a nezávislost
Před chvílí jsme nahlédli, že lineární obal dvou vektorů tvoří rovinu. Je tomu tak ale vždy? Zkuste najít vektory x1, x2, které dávají protipříklad.
Může se stát, že lineární obal bude pouze přímka, a to v případě, že je x1 násobkem x2. Poté už x2 leží ve span{x1}, takže „nic nepřidá“. Říkáme, že vektory x1, x2 jsou lineárně závislé.
Tento pojem můžeme zobecnit pro více vektorů. Vektory x1,…,xn jsou lineárně závislé právě tehdy, když lze jeden z nich vyjádřit jako lineární kombinaci zbytku. Ekvivalentně platí, že některý z těchto vektorů je nadbytečný a jeho odebráním z generátorů se lineární obal nezmění.
Na následujícím obrázku je znázorněn lineární obal tří vektorů. Libovolné dva z nich by vygenerovaly stejnou množinu.
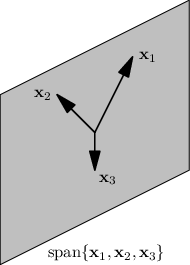
Pakliže mezi vektory není žádný závislý na ostatních, řekneme, že jsou vektory lineárně nezávislé. Podíváme-li se do učené knihy, pravděpodobně najdeme pro nezávislost jinou definici: Vektory x1,…,xn jsou nezávislé právě tehdy, když rovnice
| n |
| i=1 |
platí pouze, jsou-li všechny koeficienty ai = 0.
Uvědomme si, že je tato definice ekvivalentní. Kdyby existovala netriviální lineární kombinace (s některými koeficienty nenulovými), poté můžeme tento nenulový člen převést na druhou stranu a příslušným koeficientem rovnici podělit, čímž získáme vyjádření tohoto vektoru jako lineární kombinaci zbytku.
Přidáme jednu vlastnost: Jsou-li x1,…,xn lineárně nezávislé a
| n |
| i=1 |
poté je toto vyjádření jednoznačné, tedy existuje pouze jedna sada koeficientů ai, která tuto rovnici splní.
Zde již důkaz nemusí být na první pohled vidět. Jak vůbec ukázat, že je vyjádření jednoznačné? Využijeme důkaz sporem: Budeme předpokládat, že existují dvě vyjádření. Odtud se pokusíme dojít ke sporu s některým z našich předpokladů, v tomto případě s předpokladem lineární nezávislosti. Připomeňte si definici nezávislosti a doplňte detaily. Pokud si nebudete vědět rady, řešení najdete na konci textu.
Afinní množiny
Již umíme reprezentovat přímky, roviny atd. jako lineární obaly jejich generátorů, ovšem pouze, pokud procházejí počátkem. S tím se jistě nespokojíme. Jak popsat tyto množiny, které leží v obecné poloze, takzvané afinní množiny?
Nejprve si představíme, že afinní množinu posuneme, a to tak, aby některý její vektor v skončil v počátku. Posunutou množinu již umíme reprezentovat jako podprostor U. Posunutím zpět o vektor v získáme hledanou afinní množinu. Protože posunutí znamená ke každému vektoru z U přičíst v, značíme výsledek U + v.
Dokonce existuje afinní kombinace jako analogie dříve zavedené lineární kombinace. Podobně jako dříve chceme, aby všechny afinní kombinace vektorů x1,…,xn daly dohromady tu nejmenší afinní množinu, jež tyto vektory obsahuje.
Nejprve se zkusme zamyslet nad afinní kombinací dvou bodů x1, x2. Afinní množina, kterou hledáme, je přímka jimi určená. Jak matematicky tuto přímku popsat? Možná bude jednodušší uvážit úsečku mezi těmito body. Bod v ležící na úsečce je jakýmsi váženým průměrem krajních bodů:
Pro úsečku bychom uvažovali 0 ≤ a1 ≤ 1. Pokud povolíme libovolné hodnoty koeficientů, získáme celou přímku.
Máme tedy vzorec pro afinní kombinaci dvou vektorů. Zobecnění pro více vektorů pak je:
| n |
| i=1 |
| n |
| i=1 |
Čili vzorec zůstává stejný jako u lineárních kombinací, jen navíc požadujeme, aby součet koeficientů byl 1.
Afinní závislost můžeme zavést analogicky tak, že je některý z vektorů při generování afinní množiny nadbytečný.
Soustavy rovnic
Probravše mnoho teorie se konečně dostáváme k praktickému využití: Naučíme se řešit soustavy lineárních rovnic, jako třeba tuto:
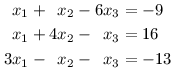
Obecně budeme mít d neznámých x1,…,xd, které sdružíme do vektoru x. Množina všech potenciálních řešení je tedy náš známý prostor Rd. Dále dostaneme n rovnic, které množinu řešení omezují.
V příkladu výše popisuje každá rovnice jednu rovinu ve třídimenzionálním prostoru. Průnik prvních dvou rovin je přímka, přidáním poslední roviny se z průniku stane jediný bod.
Obecně vymezují rovnice nadroviny, tedy afinní množiny dimenze d-1 v prostoru Rd. Průnik k nadrovin v d-dimenzionálním prostoru bude (d-k)-dimenzionální afinní množina. Pokud tedy budeme mít d nadrovin, jejich průnik bude mít dimenzi 0 a hledané řešení x bude jediný bod.
Tedy až na případy, kdy tomu tak není. Může se stát, že průnik prvních několika nadrovin je rovnoběžný s další přidávanou nadrovinou. Pak řešení existovat nebude. Případně se může stát, že průnik celý leží v nadrovině, poté se přidáním této nadroviny dimenze nesníží. V jistém smyslu je tento případ podobný lineární závislosti, také je jedna z rovnic nadbytečná. Tato spojitost není náhodná.
Úkol 2 – Nezávislost a soustavy [3b]
Když jsme zaváděli lineární nezávislost, neřekli jsme si, jak ji ověřit. K tomu nám poslouží právě soustavy rovnic. Popište, jak s jejich pomocí určit, že jsou vektory nezávislé, respektive jak najít koeficienty, které vyjádří jeden z nich jako lineární kombinaci zbytku.
Gaussova eliminace
Při řešení se budeme snažit z rovnic eliminovat neznámé tak, aby šlo jednoduše dopočítat hodnoty těch ostatních. K tomu nám budou sloužit elementární úpravy:
- Vynásobení rovnice nenulovou konstantou.
- Přičtení jedné rovnice k druhé. Případně můžeme spojit tuto úpravu s minulou a přičíst násobek jedné rovnice k druhé. Pochopitelně můžeme také odečítat.
- Výměna dvou rovnic.
Na těchto úpravách je založený algoritmus známý pod jménem Gaussova eliminace. Pojďme si ho ukázat na soustavě uvedené výše. Nejprve eliminujeme x1 ze všech rovnic kromě té první. Dosáhneme toho pomocí 2. elementární úpravy, budeme přičítat násobky první rovnice k ostatním. K druhé rovnici přičteme (-1)-násobek, ke třetí (-3)-násobek.
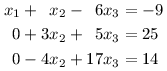
Pokračujeme eliminací x2. Při tom nesmíme znovu zanést x1 tam, kde jsme jej eliminovali, proto od teď budeme pracovat pouze s druhou a třetí rovnicí.
Chceme tedy eliminovat x2 ze třetí rovnice. Mohli bychom k ní přičíst 4/3-násobek té druhé, tím by nám však vznikly zlomky, takže raději nejprve vynásobíme třetí rovnici 3 a poté přičteme 4-násobek druhé rovnice.
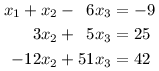
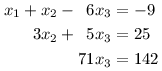
Z poslední rovnice již zvládneme dopočítat x3 = 2. Dosazením do druhé rovnice dostaneme
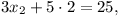
Podívejme se ještě na jeden případ, ve kterém nevyjde řešení jednoznačně.
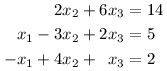
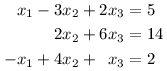
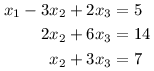
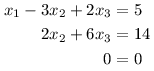
Poslední rovnice nám již nedává žádnou informaci. Alespoň platí, jinak by řešení neexistovalo. Takto je řešení více, dokonce nekonečně mnoho. Pro každou myslitelnou hodnotu x3 umíme dopočítat zbylé neznámé. Prohlásíme ji tedy za parametr a řešení vyjádříme v závislosti na něm.
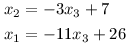
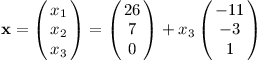
Úkol 3 – Algoritmus eliminace [7b]
Naprogramujte algoritmus Gaussovy eliminace. Na vstupu dostanete číslo d a poté d rovnic. Každá rovnice sestává z d + 1 celých čísel, prvních d určuje koeficienty u neznámých x1,…,xd, poslední číslo je pravá strana rovnice. Můžete předpokládat, že každá neznámá má v alespoň jedné rovnici nenulový koeficient.
Na první řádek výstupu vypište N, pokud řešení neexistuje,
J je-li jednoznačné, P je-li parametrizované.
V jednoznačném případě na další řádek vypište d hodnot neznámých.
V parametrizovaném případě použijte vektorový zápis (viz výše),
nejprve tedy na jeden řádek vypište hodnoty neznámých nezávislé na parametrech,
poté na dalších d řádků vypište vždy po d hodnotách. Je-li i-tá neznámá
parametrem, poté na i-tém řádku budou neznámé vyjádřené vzhledem k tomuto parametru.
Pro neparametrizované neznámé vypište d nul.
 Lehčí varianta (za 4 body):
Nemusíte řešit parametrizované případy.
Lehčí varianta (za 4 body):
Nemusíte řešit parametrizované případy.
K této úloze si nelze generovat vstupy v odevzdávátku, odevzdejte přímo zdrojový kód. Vaše řešení by mělo zejména mít rozumnou časovou složitost. Kromě toho se můžete pokusit naprogramovat algoritmus tak, aby bylo spočítané řešení přesné. Počítání s desetinnými čísly totiž vede k odchylkám.
Řešená soustava s jednoznačným řešením:
3
1 1 -6 -9
1 4 -1 16
3 -1 -1 -13
J
-2 5 2
Řešená soustava s parametrizovaným řešením:
3
0 2 6 14
1 -3 2 5
-1 4 1 2
P
26 7 0
0 0 0
0 0 0
-11 -3 1
Všechny úlohy z tohoto seriálu odevzdávejte dohromady v jednom zazipovaném archivu. Termín odevzdání je 13. listopadu 2022 ve 32:00 (tedy další ráno v 8:00). Poté lze odevzdávat za snížený počet bodů až do konce ročníku.
Řešení důkazů
Jednoznačnost lineární kombinace. Pro spor předpokládejme, že máme dvě různá vyjádření
| n |
| i=1 |
| n |
| i=1 |
Tyto rovnice od sebe můžeme odečíst.
| n |
| i=1 |
Dle předpokladu byla vyjádření různá, tudíž pro alespoň jedno i platí ai - bi ≠ 0. Tedy jsme našli netriviální lineární kombinaci, což je spor s předpokladem lineární nezávislosti vektorů x1,…,xn.