Čtvrtá série třicátého pátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 35-4-1: Golfový turnaj
- 35-4-2: Kevinovo velkolepé rozloučení
- 35-4-3: Házení
- 35-4-4: Hroší růže
- 35-4-S: Skalární součin
- 35-4-X1: Mnoho jamek
 35-4-1 Golfový turnaj (Zadání)
35-4-1 Golfový turnaj (Zadání)
Zatím ukážeme referenční řešení úkolů, které by dostalo plný počet bodů. Pokud jste nějaký úkol vyřešili za více než maximum a chcete se o něj podělit, pošlete nám svůj zdroják. Rádi ho pak vydáme v komentářích.
Číslo 2023
Naše řešení využívá prvočíselný rozklad čísla 2023 na 7·172, což je 7·(9+8)2. Z toho dostaneme následující program o 7 znacích:
98adm7m
Součet
Máme sečíst všechna čísla na zásobníku. Uděláme to tak, že dokud je na zásobníku více než jedno číslo, nahradíme horní dvě čísla jejich součtem. Program má 9 znaků:
(k1g) (a) w
(Příkaz k zjišťuje, kolik čísel na zásobníku, takže k1g
je pravdivé, pokud tam jsou aspoň dvě čísla.)
Mocnina
Jeden krok výpočtu dostane na zásobníku x, y, t a nahradí to za x, y-1, t·x. Tím pádem pokud začneme s x, y, 1, dostaneme po i krocích x, y-i, xi. Až se y vynuluje, bude na zásobníku x, 0, xy.
Program o 17 znacích vypadá takto:
1
(xd) (1s x 2c m) w
pxp
Tělo programu je tedy smyčka while s podmínkou xd. Ta vytvoří
x, t, y, y. Pokud je y > 0, opakujeme:
1s→ x, t, y-1x→ x, y-1, t2c→ x, y-1, t, xm→ x, y-1, t·x
Pokud už je y = 0, smyčka skončí a pxp způsobí,
že na zásobníku zbude t.
Největší společný dělitel
Použijeme Euklidův algoritmus s modulením. V jednom kroku chceme čísla x, y nahradit čísly y, x mod y. Programem na 11 znaků to uděláme následovně:
(d) (x 1c r) w
a
Smyčka while běží, dokud y ≠ 0. V jednom kroku x, y pomocí x
prohodíme na y, x, pomocí 1c upravíme na y, x, y a nakonec
instrukcí r vymodulíme na y, x mod y.
Po doběhnutí smyčky bude y = 0 a aktuální x bude NSD původní dvojice čísel.
Instrukcí a se zbavíme nulového y, takže zbude x.
N-té prvočíslo
Nejprve si připravíme podprogram, který pro zadané číslo x > 1 najde jeho největšího dělitele menšího než x:
d 1
() (1s 1c 1c r) w
Podívejme se na tělo cyklu (začíná 1s). To na zásobníku dostane x, d,
přičemž d je předchozí testovaný dělitel. Pomocí 1s snížíme d o 1,
načež zkopírujeme x a d a spočítáme x mod d.
Cyklus bude pokračovat, pokud x mod d ≠ 0, tedy jsme ještě dělitele nenašli. Před vstupem do cyklu uložíme na zásobník konstantu 1, abychom zařídili, že aspoň jeden průchod cyklem proběhne.
Cyklus se zastaví nalezením dělitele (nejpozději při d = 1). Na zásobníku zbude x, d.
Nyní celý program o 35 znacích:
1
(1c) (
1a
d 1
() (1s 1c 1c r) w
1e (x 1s x) i
) w
xp
V průběhu hlavní smyčky bude na zásobníku n, x, kde x je právě zkoumané číslo a n říká, kolik ještě máme najít prvočísel. Začínáme s x=1. Pak x postupně zvyšujeme a kdykoliv nalezneme prvočíslo, snížíme n o 1. Až n klesne na 0, zastavíme se.
V těle hlavní smyčky zvýšíme x o 1. Pak použijeme podprogram na nalezení největšího
dělitele d < x. Pomocí 1e zjistíme, zda d = 1, což znamená, že x je prvočíslo.
Pokud ano, odečteme od n jedničku.
Na konci smažeme n a zbude x. (Mohli jsme použít trik z předchozího úkolu a jelikož
n = 0, nahradit xp za a. Referenční řešení to nicméně nedělalo.)
Třídění
Použijeme bublinkové třídění: posloupnost budeme procházet zleva doprava a kdykoliv narazíme na dvojici, která je ve špatném pořadí, prohodíme ji. Až dojedeme na konec, podíváme se, zda došlo k nějakému prohození, a pokud ano, algoritmus spustíme znovu.
Z toho vychází následující program o 43 znacích:
1
() (
0 k
(d 2s) (
dc 1cc
d 2c l (x 31o) i
2cxo 1cxo
1s
) w
p
) w
Nejprve se zaměříme na tělo vnitřní smyčky (nejvíce odsazenou část programu). Když do něj vstoupíme, zásobník obsahuje x1, … , xn, s, i. Zde s je 0 nebo 1 podle toho, zda už došlo k nějakému prohození. Proměnná i ukazuje na místo v posloupnosti, kde zrovna porovnáváme; ovšem indexy počítáme trochu zvláštně: od polohy i doleva. Takže pro i = 2 indexujeme xn, zatímco pro i = n+1 indexujeme x1. Indexovanému prvku říkejme x[i].
Instrukce dc na zásobník uloží prvek x[i].
Následující 1cc nejprve zkopíruje i a pak znovu indexuje i-čkem.
Leč v této době už je na zásobníku x[i], takže indexy jsou o 1 posunuté
a přečteme x[i-1].
Teď máme na zásobníku:
Následující d 2c l zkopíruje x[i-1] a x[i] a kopie porovná.
Pokud bylo x[i-1] < x[i], pak tyto dva prvky prohodíme (zatím jenom na vrcholu zásobníku)
a pomocí 31o nastavíme s na 1.
Nakonec x[i] a x[i-1] zapíšeme zpět na původní pozice instrukcemi 2xco 1cxo.
Smyčka končí snížením i o 1. Nyní přemýšlejme, jak smyčka začne a skončí.
Před jejím začátkem uložíme na zásobník s = 0 a pomocí k spočítáme prvky na zásobníku.
Tím inicializujeme i na n+1. Smyčka pak pokračuje, dokud i ≠ 2. Projde tedy postupně
všechny dvojice sousedních prvků zleva doprava.
Nakonec zbývá vnější smyčka: Po dokončení vnitřní smyčky odstraníme i (instrukce p)
a pokud s ≠ 0, pokračujeme dalším průchodem.
 35-4-2 Kevinovo velkolepé rozloučení (Zadání)
35-4-2 Kevinovo velkolepé rozloučení (Zadání)
Představme si, že Kevin na střechu napsal tuto zprávu:
cestu! hezkou Zuzko, AhojJako první otočíme pořadí znaků. Toho dosáhneme prohazováním prvního znaku s posledním, druhého s předposledním, dokud se indexy prohozených znaků nepřekříží. Tímto způsobem bude muset Kevin nést jen jednu tašku najednou. Protože si pamatujeme jen indexy obou prohazovaných znaků, splníme požadavky na paměť. Náš ukázkový vstup se tímto postupem promění v následující:
johA ,okzuZ uokzeh !utsecNyní jsou sice samotná slova ve správném pořadí, ale jejich znaky ne. Tedy budeme muset pole projít znovu. Tentokráte najdeme, kde jednotlivá slova končí a začínají, a prohodíme jejich znaky stejně, jako jsme to na začátku udělali s celou zprávou. Pak už bude zapsaná správně.
Prohození celé zprávy nám zabere O(N) času, nalézt konce a začátky slov také. Samotné prohození znaků ve slově zabere lineární čas vzhledem k délce slova. Výsledná časová složitost tedy bude O(N + N + N) = O(N).
 35-4-3 Házení (Zadání)
35-4-3 Házení (Zadání)
Našim cieľom je nájsť hod s čo najmenšou počiatočnou rýchlosťou, ktorý doletí do určenej vzdialenosti. Pokiaľ by v ceste nestáli žiadne prekážky, takýto optimálny hod by určite letel pod uhlom 45 °. Toto dokazovať nebudeme, pretože ide o všeobecne známy fakt, ale môžeme to tiež vidieť z grafu priebehu funkcie pomeru preletenej vzdialenosti k použitej sile (vzorce odvodíme nižšie):
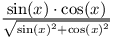
Všimnime si, že na to, aby sme reprezentovali jeden konkrétny hod, nám stačí poznať buď jeho uhol, alebo počiatočnú rýchlosť – druhú hodnotu potom dokážeme vypočítať, keďže poznáme miesto dopadu. Omnoho praktickejšie je ale reprezentovať hody pomocou vertikálnej a horizontálnej zložky rýchlosti, z ktorých si vieme vypočítať aj celkovú rýchlosť (pomocou Pytagorovej vety), aj uhol (tangens uhlu je pomer vertikálnej a horizontálnej zložky rýchlosti). Zároveň funkcia tangens je na intervale (0 °, 90 °) prostá a rastúca, takže vieme uhly porovnávať a triediť aj pri takejto reprezentácii.
Optimálny hod pod uhlom 45 ° má pomer rýchlostí rovný 1. Všetky hody pod jeho trajktóriou majú pomer menší než 1, nad trajektróriou väčší.
Pre každý obdĺžnik vieme nájsť dva hody, ktoré ho ohraničujú zhora a zdola. Budeme si samostatne pamätať obdĺžniky, ktoré nás limitujú nad a pod optimálnou trajektóriou. Keď načítame všetky obdĺžniky a roztriedime si ich takto (jeden obdĺžnik môže byť aj v oboch kategóriach, ak ním prechádza optimálna trajektória), dostaneme intervaly, ktoré sa prekrývajú. Každý interval reprezentuje zakázané uhly hodu, čiže také uhly, ktoré spôsobia, že hod narazí do daného obdĺžnika. Za začiatok intervalu budeme považovať hod bližší 45 ° a za koniec ten vzdialenejší. Z oboch skupín chceme nájsť koniec takého intervalu, že žiadny iný skôr začínajúci interval ho neprekrýva – teda každý interval, ktorý začal bližšie k 45 ° než hľadaný koniec, aj skončil skôr. Takto nájdeme najbližší hod k 45 °, ktorý neleží v žiadnom intervale, a teda ho neblokuje žiadny obdĺžnik.
Intervaly si utriedime podľa začiatku (súradnice hodu bližšej k 45 °) a potom prechádzame postupne. Počas toho si pamätáme najvzdialenejší koniec intervalu, ktorý sme zatiaľ videli. Ak nasledujúci interval začína skôr, než je zapamätaný koniec, posunieme sa na tento nový interval a skúsime, či jeho koniec neleží ešte neskôr, než zapamätaný. Keď sa nám podarí ukončiť interval skôr, než začneme ďalší, nájdeme prvé miesto, kde nám hod nič neblokuje. Takéto hraničné hody nájdeme pre hody pod aj nad 45 ° a zoberieme lepší z oboch nájdených (taký, pre ktorý výjde výsledná potrebná rýchlosť menšia).
Už len stačí vymyslieť, ako zistiť pre každý obdĺžnik hraničné body. Parabola sa môže obdĺžnika dotýkať v piatich bodoch. Štyri z nich sú rohy, piaty leží na spodnej strane – tam sa môže dotýkať iba vrchol paraboly. Je zrejmé, že vrchné body obdĺžnika limitujú parabolu zospodu viac, než spodné body, a naopak. Pre nájdenie vrchného okraju intervalu nám teda stačí porovnať hody prechádzajúce vrchými rohmi obdĺžnika, a zobrať ten vyšší. Pre nájdenie spodného intervalu zase porovnáme hody cez spodné rohy, a pokiaľ prechádza obdĺžnik ponad stred vzdialenosti, tak aj hod cez daný bod na jeho spodnej strane, kde by mohol byť vrchol paraboly.
Teraz vzorce:
Pozrime sa na to, ako vyzerajú rovnice pre let lopty, konkrétne pre jej jednotlivé momentálne rýchlosti vx a vy, výšku y a vzdialenosť x vzhľadom na počiatočné rýchlosti vx0 a vy0, čas t a tiažové zrýchlenie g:
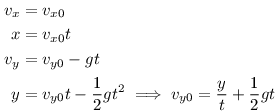
Zaujímavé pozorovanie vieme spraviť o tiažovom zrýchlení. Totiž ak by sme ho napríklad zvýšili desaťkrát a hodili hod s rovnakou horizontálnou aj vertikálnou počiatočnou rýchlosťou, lopta bude letieť desaťkrát kratšie, kým spadne, teda vyletí do desaťkrát menšej výšky, a preletí desaťkrát menšiu vzdialenosť. Aby nový hod doletel rovnako daleko, ako pôvodný, a pritom pomer rýchlostí zostal rovnaký, museli by byť nové počiatočné rýchlosti obe √10-krát väčšie, než pôvodné.
To ale znamená, že môžeme úlohu riešiť pre tiažové zrýchlenie rovné jednej, a nakoniec len preškálovať výsledok odmocninou z 9,81. Alebo dokonca zrýchlenie z rovníc odstráňme! Zjednodušíme si tým odvodzovanie, ale musíme si dať pozor, aby všetko zostalo fyzikálne zmysluplné.
Pre každý bod otrebujeme nájsť počiatočné rýchlosti pre parabolu, ktorá prechádza bodmi (M, 0) (koncový bod) a (x, y) (zadaný bod). Označme si t1 čas, za ktorý sa dostaneme do bodu (x, y) a t2 čas, za ktorý sa dostaneme do (M, 0). Keďže tiažové zrýchlenie je 1, platí, že t2 = 2vy0 (najskôr letíme nahor a potom rovnako dlho nadol), a teda M = 2vx0vy0 (čas letu krát horizontálna rýchlosť).
Použijeme poslednú rovnicu a vyjadríme si čas dosiahnutia bodu x, y zo známych veličín:
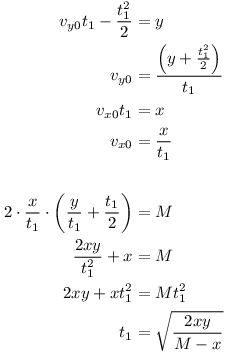
Teraz ľahko dopočítame začiatočné rýchlosti:
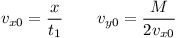
Takto vieme získať čas a následne rýchlosti pre každý bod so známymi súradnicami.
Časová zložitosť celého riešenia je O(N log N), keďže pre každý obdĺžnik robíme konštantný počet operácii, ale potom musíme zoznam až O(N) bodov utriediť, aby sme mohli nájsť najlepšiu trajektóriu. Pamäťová zložitosť je O(N), pre každý obdĺžnik si pamätáme konštantný počet údajov.
 35-4-4 Hroší růže (Zadání)
35-4-4 Hroší růže (Zadání)
Nejdřív si všimněme, že tato úloha ve skutečnosti mluví o orientovaných grafech. Políčka reprezentují vrcholy a skluzavky hrany.
Pojďme nejdříve problém vyřešit pro jednu komponentu. Podívejme se tedy, jak vypadá. Všimněme si, že určitě nemůžeme mít dva cykly v jedné komponentě. Proč? Uvažujme cykly o délkách k, ℓ a spojení (cesta, ale nerespektuje orientace hran) mezi nimi hranové délky d. Tento podgraf má k+ℓ+d-1 vrcholů, ale k+ℓ+d hran, takže by musely z nějakého vrcholu vést dvě hrany. (Ještě by mohly být dva cykly v sobě, ale všimněme si, že v takovém případě jejich poslední společný vrchol má alespoň dvě vycházející hrany.)
V cyklech se můžeme dostat z každého vrcholu do každého, takže je můžeme nahradit jedním vrcholem (až budeme přidávat hrany z/do tohoto vrcholu, stačí je přidat do libovolného v cyklu.)
Nyní je naše komponenta strom (když odebereme orientaci hran). Všimněme si, že ať už začneme na libovolném vrcholu a půjdeme po hranách, dokud to půjde, vždy skončíme ve stejném vrcholu. (Spojení mezi dvěma cílovými vrcholy by mělo vrchol s dvěma hranami, protože z každého nevede žádná hrana ven.) Tomuto vrcholu říkejme nejhlubší vrchol komponenty (NVK).
Do vrcholů s žádnými vstupními hranami (říkejme jim vrchní) budeme muset určitě jednu přidat. Přidejme tedy do všech hranu z NVK. Pak mezi každými dvěma vrcholy bude existovat cesta: Z prvního dojdeme do NVK, z NVK do vrchního vrcholu nad druhým a z něj do druhého.
A co kdyby komponent bylo více? Očíslujme si komponenty 0 až K-1 a připojujme hrany z NVK i-té komponenty do vrchních vrcholů (i+1)%K-té komponenty. Potom se vždy můžeme dostat do předchozí komponenty a z ní jen vybrat správný vrchní vrchol. Podotkněme, že přidáme určitě nejmenší počet hran, protože do každého vrchního vrcholu musí vést alespoň jedna a my nepřidáme žádnou navíc.
A jak bude vypadat náš algoritmus? Nejdřív si prohledáním najdeme komponenty souvislosti. Poté si projdeme každou komponentu do hloubky a pokud se v ní vyskytuje cyklus, tak ho smrskneme. (Vrcholy v cyklu jsou mezi oběma výskyty dvakrát navštíveného vrcholu.) Následně projdeme všechny vrcholy komponenty a najdeme všechny vrchní vrcholy (mají 0 vstupních hran) a NVK (má 0 výstupních hran). Nakonec pouze přidáme hrany mezi komponentami.
Kroky výše zmíněného algoritmu realizujeme buď prohledáváním do hloubky nebo prostým projitím všech vrcholů, a proto naše celková časová složitost je Θ(N), stejně tak paměťová.
 35-4-X1 Mnoho jamek (Zadání)
35-4-X1 Mnoho jamek (Zadání)
Ze zadaných limitů vyplývá, že kvadratický algoritmus nebude stačit. Nabízí se tedy Mergesort nebo Quicksort. Mergesort by však potřeboval dost pomocné paměti a na zásobníku nám zbývá místo pouze na 200 čísel. Použijeme tedy Quicksort, který lze naprogramovat tak, aby pracoval v původním poli. Konkrétně budeme vycházet z následující implementace:
# setřídí polouzavřený interval [begin, end)
def quicksort(arr, begin, end):
if end - begin <= 1:
return
# zvolíme první prvek jako pivot
swap = begin
for i in range(begin + 1, end):
if arr[i] < arr[begin]:
swap += 1
arr[i], arr[swap] = arr[swap], arr[i]
# přesuneme pivot na správné místo
arr[swap], arr[begin] = arr[begin], arr[swap]
quicksort(arr, begin, swap)
quicksort(arr, swap + 1, end)
Režie rekurze
Tento algoritmus však vyžaduje rekurzi, kterou náš počítač neumí. Budeme ji tedy muset simulovat pomocí zásobníku. Na zásobník si uložíme indexy určující začátek a konec úseku pole, který chceme setřídit. Program poběží ve smyčce, která si vždy přečte tyto indexy ze zásobníku a daný úsek zpracuje. Má-li úsek délku nejvýše 1, není jej třeba třídit, takže jen smažeme indexy a pokračujeme další iterací. Je-li úsek delší, rozdělíme jej na dvě části podle pivotu a přidáme na zásobník indexy pro oba úseky, aby se rekurzivně zpracovaly.
Ještě potřebujeme program nějak ukončit, jinak by se smyčka nikdy neukončila a prvky pole by se interpretovaly jako indexy. Jednoduše tedy za poslední prvek pole přidáme vhodnou zarážku. Zásobník v průběhu výpočtu tedy bude vypadat zhruba takto:
[data] [zarážka] [end begin] [end begin]
Ukládáme end před begin, to je spíše implementační detail,
který nám trochu usnadní práci při dělení na dva úseky.
Zajímavější je rozmyslet si, jak přesně budeme pole indexovat.
Instrukce copy a over počítají od vrcholu zásobníku, který se posouvá,
takže dvě hodnoty begin ukazující na stejný prvek budou nutně různé.
Zavedeme si konvenci, že oba indexy počítají tak, že begin leží na indexu 0.
Tím pádem budou první indexy popisující celé pole 2 a n+2
(vzpomeňte si, že end ukazuje na prvek za koncem pole).
Jako zarážku můžeme zvolit třeba 0, protože takový index nikdy nevznikne.
Takto může vypadat zásobník na začátku a po první iteraci:
[2 3 1 4 0] [0] [2 7]
[1 0 2 4 3] [0] [5 7] [4 6]
Implementace
Režii rekurze již máme rozmyšlenou, můžeme se dát do psaní. Jak jsme již nastínili dříve, program bude vykonávat jednu velkou smyčku. Ta se vždy podívá, jestli je na zásobníku zarážka, a pokud ne, provede tělo funkce.
Trochu náročné bude zpracování podmínky.
Buď chceme rekurzi ukončit a smazat indexy, nebo rozdělit úsek na dvě menší části.
Potřebujeme tedy konstrukci if – else.
Jazyk ovšem nabízí pouze if.
Vyřešíme to tím, že na zásobník umístíme hodnotu určující, jestli se má druhá větev vykonat.
Výchozí hodnota bude 1, pokud však podmínka vyjde a provede se první větev,
přepíšeme tuto hodnotu na 0.
Cyklus rozepíšeme pomocí while,
začneme indexem begin a v každé iteraci jej snížíme o 1.
Ano, snížíme, protože indexy směrem doprava klesají.
Když rozdělíme prvky podle pivotu, zbývá na zásobník uložit indexy nových úseků. Zde si musíme znovu dát pozor na klesající indexy a také na to, že druhá dvojice bude posunutá o 2.
Zbytek programu již není složitý, celý včetně komentářů jej najdete níže. Počet instrukcí by jistě šel ještě trochu snížit.
 35-4-S Skalární součin (Zadání)
35-4-S Skalární součin (Zadání)
Úkol 1 – Mnohoúhelník [4b]
Představme si, že obcházíme po obvodu mnohoúhelníku po směru hodinových ručiček. Je-li bod x neustále po naší pravé ruce, pak leží uvnitř mnohoúhelníku. Pokud se někdy ocitne nalevo od nějaké hrany, pak leží mimo.
Podívejme se na hranu pi pi+1. Chceme vymyslet, jak zjistit, na jaké straně od ní leží bod x. Skalární součin umí jen zjistit úhel mezi dvěma vektory, musíme tedy nějaké vhodné vyrobit. Zvolíme u = pi+1 - pi (vektor od prvního bodu hrany k druhému) a v = x - pi (vektor od prvního bodu hrany k x). Pokud by v ležel vpravo od u, pak i bod x leží vpravo od hrany.
Jenže, my umíme jen změřit úhel mezi dvěma vektory. Již nezjistíme, který z nich leží vpravo. Nevadí, pořídíme si vektor n kolmý na hranu, tedy na vektor u. Takové kolmé vektory jsou dva, my si vybereme ten, který směřuje dovnitř mnohoúhelníku. Spočítáme jej jednoduše, pokud je u = (a, b)⊤, poté bude n = (b, -a)⊤. Pak už stačí vypočítat skalární součin ⟨n,v⟩. Bude-li kladný, mají vektory stejný směr, tedy v leží vpravo od hrany.
To už vypadá slibně. Náš postup však má stále jeden háček. Zadání nám neříká, jestli jsou vrcholy mnohoúhelníku zadané po směru nebo proti směru. Naštěstí to nemusíme řešit, stačí postup zopakovat pro obě varianty. Pokud v jedné z nich vyjde, že x leží na stejné straně od všech hran, pak leží uvnitř.
Spočítáme celkem 2n skalárních součinů, každý z nich v konstantním čase. Výsledná časová složitost je tedy O(n).
Úkol 2 – Vzdálenost od roviny [6b]
Rovina ρ tvoří afinní prostor. Lépe se však pracuje s vektorovými prostory (tedy s prostory procházejícími počátkem). Otázku proto upravíme, budeme hledat vzdálenost bodu y = x - c = (5, 1, 0)⊤ od roviny σ= span{ u1, u2 } , což je ekvivalentní.
Naším plánem bude najít yσ, projekci vektoru y do roviny σ. Když pak tuto projekci od y odečteme, získáme vektor n kolmý na rovinu, jehož norma odpovídá hledané vzdálenosti.
Začneme nalezením ortonormální báze σ. První vektor stačí normalizovat:
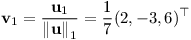
Druhý vektor musí být kolmý na první:
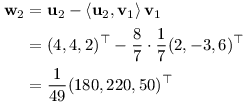
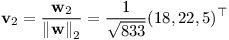
Nyní tedy umíme spočítat n:
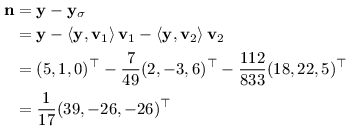
Zbývá spočítat normu tohoto vektoru a zjistíme hledanou vzdálenost:
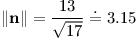
Úkol 3 – Fyzikální měření [5b]
Hledáme přímku s předpisem m = pt + q. Vytvoříme soustavu rovnic s neznámými p, q:
| 0p + q | = 67 |
| 3p + q | = 66 |
| 10p + q | = 63 |
| 14p + q | = 62 |
| 20p + q | = 60 |
Převedeme soustavu do maticového zápisu a použijeme metodu nejmenších čtverců:
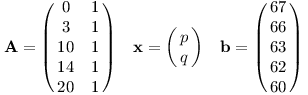
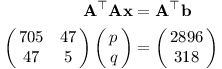
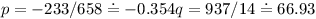
Zbývá odpovědět, kdy se všechen dusík vypaří. Hledáme tak řešení rovnice
kterým je t = 44039/233 ≐189. Bude to tedy 189 s od začátku měření.