Čtvrtá série dvacátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 26-4-1: Kamínkový solitér
- 26-4-2: Výroba amuletu
- 26-4-3: Obnovené spojení
- 26-4-4: Skládání mapy
- 26-4-5: Místo pro tábor
- 26-4-6: Sněhová bitva
- 26-4-7: Královští špioni
- 26-4-8: Dlaždičky
26-4-1 Kamínkový solitér (Zadání)
Mnoho řešitelů odeslalo správná řešení, to nás moc těší.
Lehčí varianta
Lehčí varianta byla, jak mnozí poznali, Euklidův algoritmus na zjišťování největšího společného dělitele (nsd). Viz kuchařku o teorii čísel.
Správnou odpovědí tedy bylo, že nám na každé hromádce zbude nsd(a,b), kde a a b jsou počty kamínků na jedné a druhé hromádce.
Někteří řešitelé si povolili odčítat i stejně velké hromádky od sebe, to pak vede k tomu, že celkový počet zbylých kamínků bude nsd(a,b).
Těžší varianta
Jak se nám změní úloha pro více hromádek?
S hromádkami, které mají 0 kamínků, se vypořádáme tak, že je prostě zahodíme, ty nám nijak nemohou ovlivnit průběh hry ani celkový výsledek (protože odečtením této hromádky od jiné se stav hry nezmění).
Nyní musíme dokázat, že nsd(a,b,c) = nsd(a,nsd(b,c)).
Víme, že a > 0, b > 0, c > 0 (jinak bychom je neuvažovali mezi hromádky). Dále platí, že a = g·a', b = g·b', c = g·c'. Navíc platí, že nsd(b,c) = g·z', protože nsd(b,c) získáme odečítáním hromádek b a c od sebe. Vždy tu vyšší odčítáme od té nižší, a tím zůstane g zachováno. To platí proto, že b-c = (g·b') - (g·c') = g ·(b'-c'). Pak platí, že pokud g = nsd(a,b,c), pak i nsd(a, g ·z') = g.
Tedy správná odpověď byla, že na každé hromádce zbude nsd(hi), případně že zbude právě nsd(hi) (pokud si řešitel povolil odčítat od sebe i stejně velké hromádky). Dokázané pozorování nsd(a,b,c) = nsd(a,nsd(b,c)) využijeme pro náš algoritmus, který bude umět v O(1) poradit další tah hry. Algoritmus bude vypadat takto:
Nejprve zahodíme hromádky, které mají hodnotu 0. Nyní vezmeme 1. a 2. hromádku, odčítáme vždy od větší menší, dokud nemají stejnou hodnotu (která je, jak už víme, nsd původních hodnot těch dvou hromádek). Poté to samé provedeme s 2. a 3. (zde dostáváme nsd původních hodnot všech předchozích hromádek a té aktuální), pak se 3. a 4., …, (n-1)-tou a n-tou. Tím jsme získali na n-té a (n-1)-té hromádce nsd všech hromádek. Nyní potřebujeme tento dělitel dostat k předchozím. Tedy provedeme odčítání hromádek zpětně (nejprve s hromádkou n-1 a n-2, pak s n-2 a n-3, …, 1 a 2). Když skončíme, máme na všech nenulových hromádkách nsd(hi) a 0 na nulových.
26-4-2 Výroba amuletu (Zadání)
Úloha se značně podobá známému problému hledání nejdelší společné podposloupnosti, popsanému např. na Wikipedii, včetně velice přímočarého řešení. Zmiňujeme se o něm i v naší kuchařce o dynamickém programování, ale algoritmus popsaný tam by se hůře upravoval pro potřeby naší úlohy.
Předpokládejme nejdříve pro jednoduchost, že ceny všech korálků jsou stejné, cR=cG=cB=1. Upravený amulet bude obsahovat tři druhy korálků: nové (které jsme vyrobili pro potřebu hesla), recyklované (které jsme použili z původního amuletu jako součást hesla) a zbytečné (které zbyly z původního amuletu, ale nejsou použity k vytvoření hesla).
My hledáme řešení s co nejméně novými korálky. Ale ježto nových a recyklovaných dohromady je vždy stejně (jako délka hesla), můžeme zrovna tak hledat řešení obsahující nejvíce recyklovaných korálků. Vzhledem k tomu, že recyklované korálky tvoří (z definice) společnou podposloupnost amuletu a hesla, můžeme použít algoritmus z odkazovaného článku pro nalezení jejich nejdelší společné podposloupnosti (NSP), a tak zjistit, které korálky chceme v optimálním řešení recyklovat.
Ukažme si to na příkladu pro amulet RRRGGGBBB a heslo
RGBRGB:
Původní amulet RRRG GGBBB
Heslo R GBR GB
Nejdelší spol. podposl. R G GB
Vyrobeno BR
Nový amulet RRRGBRGGBBB
Typ korálku rzzrnnzrrzz
Z výstupu algoritmu kromě samotné podoby NSP (RGGB)
snadno zjistíme, i na jakých pozicích
v amuletu a hesle se tyto
recyklované korálky budou nacházet. Jedním průchodem NSP
si tedy můžeme ke každému recyklovanému korálku uložit jeho
pozici v původním amuletu, a z toho už snadno dopočítáme,
kam se vkládají korálky nové.
Tady je trochu problém s interpretací zadání, neboť přidáváním nových korálků se nám původní posouvají a není příliš jasné, co vlastně znamená „i-tý korálek“. V příkladu výše nejprve vypíšeme „vlož modrý korálek za čtvrtý“ a pak červený za … čtvrtý, nebo pátý? Nejjednodušším způsobem, jak se problému elegantně zcela vyhnout, je vypisovat přidané korálky odzadu. Tak nám žádný přidaný korálek nemůže ovlivnit číslování míst, na která budeme přidávat později. V našem případě by to tedy znamenalo nejdříve vložit červený korálek za čtvrtý a pak modrý za čtvrtý (čímž se červený odsune o jednu pozici doprava).
Složitosti algoritmu dominuje hledání NSP, které zvládneme v čase a paměti O(|A| · |H|), kde |A| je délka původního amuletu a |H| je délka hesla. Zbývá se vypořádat s tím, že výrobní ceny korálků nemusí být jednotkové. Ale není těžké si rozmyslet, že algoritmus NSP můžeme jednoduše upravit tak, aby místo nejdelší hledal nejdražší společnou podposloupnost. Prostě všude místo délek posloupností počítáme jejich ceny a při rozšiřování posloupnosti místo jedničky přičítáme cenu přidávaného korálku. Složitost tím nijak neovlivníme. Pro přesnou podobu upraveného algoritmu nahlédněte do programu.
26-4-3 Obnovené spojení (Zadání)
V této úloze se nám bohužel vloudila chyba do zadání úlohy, kde mělo být uvedeno, že jeskyně, které mezi sebou propojujeme, si očíslujeme od 1 do n. Proto se řada z vás spokojila s triviálním řešením pomocí třídění nebo pomocí hešování. Chyba je ovšem na naší straně, takže jsem taková řešení jen mírně bodově odlišil od těch, která si chybějící předpoklad domyslela a byla zcela správně.
Optimálním řešením je dvojité užití přihrádkového třídění. Nejprve si každou dvojici jeskyň uspořádáme vzestupně. Nyní roztřídíme dvojice do přihrádek podle hodnoty druhé jeskyně. V praxi to můžeme reprezentovat třeba polem spojových seznamů délky n, kde ke každé hodnotě druhé jeskyně budeme mít spojový seznam hodnot první jeskyně. K druhému třídění využijeme výsledek prvního. Budeme postupně procházet každý spojový seznam od nejmenší hodnoty druhé jeskyně k největší a zatřiďovat do jiných přihrádek tentokrát podle první jeskyně. Všimněme si, že pokud k jedné první jeskyni existují dvě druhé, tímto průchodem jako první narazíme na tu s menším číslem. Z toho vyplývá, že čísla ve výsledných přihrádkách budou setříděná od nejmenšího k největšímu.
Tím jsme dostali všechny dvojice setříděné primárně podle první a sekundárně podle druhé jeskyně. Takto setříděná data už snadno projdeme a vyhneme se při vypisování duplikátům například tak, že si pamatujeme, co jsme naposledy vypsali.
Zacházeli jsme s O(n) přihrádkami a s O(m) jeskyněmi, přitom jsme na každou jeskyni spotřebovali konstantní čas při jejím zapracování do některého seznamu, výsledná časová i paměťová složitost tohoto řešení je tedy O(n + m).

26-4-4 Skládání mapy (Zadání)
Častou chybou u úlohy bylo to, že jste předpokládali celočíselnost souřadnic a pokoušeli jste se obdélníky s mapou napasovat do nějaké tabulky, o celočíselnosti jsme však nic neslíbili. Ta by se sice dala zachránit nějakou kompresí souřadnic (seřadili bychom si neceločíselné souřadnice za sebe a očíslovali), ale větší problém byl v tom, že taková tabulka by mohla být obrovská – představte si dva malé kusy mapy vzdálené od sebe milion políček. Inicializace takové tabulky by nám zabrala neúměrně mnoho času, a proto bylo nutné vydat se jinudy.
Nejdříve se zkusíme zamyslet nad tím, jak by se úloha řešila jen v jednom rozměru, tedy kdybychom namísto obdélníků měli jen úsečky na přímce. Takový případ je přesně stvořený pro zjednodušený intervalový strom.
Intervalový strom nám ve zkratce umožňuje provádět dotazy nad intervaly, tedy s kterými intervaly se protíná hledaný interval. My ale hledáme jen jeden bod a navíc nás zajímá jen počet obdélníků mapy, se kterými se protneme, proto nám stačí použít jednodušší verzi intervalového stromu.
Z původního intervalového stromu si vypůjčíme jen vyhledávání podle konců pokrytých intervalů ve vnitřních vrcholech, a protože naše dotazy půjdou vždy až do samotných listů intervalového stromu, stačí nám mít počty pokrytých intervalů jen v těchto listech. Později u dvourozměrné varianty budeme muset do vnitřních vrcholů přidat nějaké další hodnoty, ale u jednorozměrné verze bez nutnosti měnit intervaly za běhu si vystačíme s touto lehčí verzí.
Takový strom si lehce postavíme v čase O(N log N) (kde N je počet úseček) tak, že si nejdříve setřídíme souřadnice začátků a konců úseček, budeme je postupně procházet (za začátek přičteme jedničku k aktuálnímu počtu pokrytých úseček, za konec zase odečteme) a ukládat do listů úplného binárního stromu. Při obcházení stromu navíc ještě do vnitřních vrcholů uložíme konce intervalů (pro vyhledávání) a jsme hotovi. Vyhledání pak lehce zvládneme v čase O(log N) na dotaz.
Dva rozměry
Jak postup výše zobecnit pro dva rozměry? Ano, použijeme dvourozměrné intervalové stromy. Nejdřív si vyrobíme intervalový strom pro jeden rozměr (jako kdybychom kusy mapy promítli jako úsečky třeba na osu x). Tím si rovinu rozdělíme na jednotlivé (v tomto případě svislé) pásy, kde máme jen spodní a vrchní okraje obdélníků mapy. Ještě však potřebujeme vyhledat správnou oblast uvnitř těchto pásů.
Proto si v každém listu prvního intervalového stromu ubytujeme další intervalový strom, který bude mít na starost pouze tento pás (každý pás si totiž můžeme zase představit jako úsečky v ose y odpovídající jednotlivým kusům mapy). Vyhledání je pak dvoustupňové: nejdříve v prvním stromě najdeme správný pás a v tomto pásu pomocí odpovídajícího stromu najdeme přesné místo, kde je umístěn bod, na který se ptáme. Takový dotaz zvládneme v O(log N).
S dvourozměrnými intervalovými stromy se ale musí opatrně – spousta zdrojů sice uvádí, že se dají vybudovat v čase O(N log 2 N), ale to jen, pokud se na ně uplatní nějaký trik. Ti z vás, kteří použili ve svých řešeních pojem 2D-intervalového stromu jako všemocný blackbox bez toho, aby se nad ním a jeho použitím a problémy zamysleli, nějaký ten bod bohužel ztratili.

Pokud by totiž obdélníky vypadaly třeba jako na obrázku výše, budeme mít řádově N intervalů v prvním (x-ovém) stromě a každý z y-ových stromů bude také držet řádově N intervalů. Pokud si budeme každý z menších stromů ukládat samostatně, dostaneme se na paměť O(N2), a k jejich konstrukci tedy i na stejnou časovou složitost.
Persistentní datová struktura
Největším problémem konstrukce našeho 2D-intervalového stromu bylo to, že stromy v druhé úrovni vypadaly pořád skoro stejně, ale pokaždé jsme je museli konstruovat celé znovu. Nedá se nějak využít již dříve zkonstruovaných stromů?
Dá, a takovému triku se říká persistence. V našich stromech vedou všechny hrany jen dolů (nepotřebujeme zpětné hrany do otce), a tak klidně můžeme udělat to, že si zkonstruujeme nový strom tak, že se bude odkazovat na části již postavených stromů. Stačí se držet základního pravidla persistence: Staré hodnoty nikdy neměním, když potřebuji něco změnit, vyrobím si od toho kopii.
Kdybychom například chtěli ve stromu níže změnit hodnotu ve vrcholu s číslem 3, stačí nám vyrobit si kopii tohoto vrcholu, kopii jeho otce (a tak dále, až ke kopii jeho kořenu) a ty odkázat na již existující podstromy. Když se nyní vydám z kořene 1', budu mít k dispozici nový strom, ale když se vydám z kořene 1, uvidím strom v původním stavu. Máme tedy dva stromy velikosti N, ale výrobou nového jsme museli strávit pouze čas O(log N) (délku cesty z vrcholu do kořene).
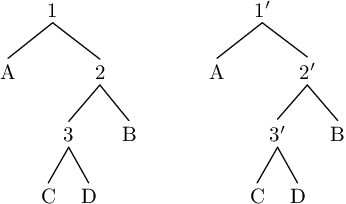
V našem případě persistenci použijeme k vyrábění jednotlivých intervalových stromů v pásech. Mezi jednotlivými pásy dochází jen k tomu, že nějaký obdélník zmizí, nebo se jiný objeví, tedy potřebujeme přičíst nebo odečíst nějakou hodnotu od nějakého intervalu hodnot. Počkat, co když ale budeme muset modifikovat řádově N vrcholů oproti předchozímu stromu, nepokazí se nám časová složitost?
Kdybychom to dělali jako dosud (se zjednodušenými intervalovými stromy), tak by se pokazila. Teď už budeme potřebovat plné intervalové stromy (tak, jak jsou popsané v kuchařce), které nám umožňují i rychlou aktualizaci hodnot. Pokud chceme modifikovat nějaký celý interval, můžeme to rozložit na modifikaci O(log N) vrcholů intervalového stromu (do vnitřních vrcholů si přičteme nějaké plus a mínus jedničky, přes které pak při dotazu projdeme a vezmeme je v potaz).
Modifikace každého vrcholu v persistentním intervalovém stromu nám trvá O(log N), takže nám (kromě prvního) výroba každého z O(N) intervalových stromů trvá O(log 2 N) a zabere maximálně stejně paměti. Vyhledávání v nich je pak stejné jako v minulém případě.
Dohromady tedy potřebujeme na výrobu celé struktury čas O(N log 2 N) a na Q dotazů čas O(Q log N). Paměti nám stačí O(N log 2 N).
Poznámka: Algoritmus můžeme ještě trochu vylepšit, pokud si všimneme, že při přidávání či odebírání obdélníka sice upravujeme až logaritmický počet vrcholů, ale všechny leží v blízkém okolí dvou cest z kořene do listu. Pokud persistenci naučíme zaznamenat všechny tyto změny najednou, zkopírujeme celkově jen O(log N) vrcholů stromu, takže výroby struktury klesne na O(N log N).
Dalšími triky by šlo snížit paměťové nároky na O(N log N), ale to už se do tohoto textu nevejde. Kdybyste chtěli, příležitostně se zeptejte :)
26-4-5 Místo pro tábor (Zadání)
Úlohu budeme řešit jen pro těžší variantu. Řešení lehčí varianty je úplně stejné, akorát jen v jednom rozměru. Zadáním úlohy je najít obdélník velký r ×s, kde potřebujeme převézt co nejméně hlíny na jeho vyrovnání. Tedy takový, v kterém na políčkách pod průměrnou výškou obdélníka chybí co nejméně hlíny. Pro další část řešení zadefinujeme n = rs a N = RS.
Pokud v daném obdélníku máme průměrnou výšku V a právě k políček s podprůměrnou výškou p1, … , pk, musíme převézt právě
| k |
| j=1 |
hlíny. Chtěli bychom tedy pro všechny možné obdélníky r ×s tyto hodnoty spočítat.
Nejdříve spočítáme průměrné výšky. Pomocí dvourozměrných prefixových součtů snadno zvládneme spočítat součty výšek v obdélnících v čase O(RS) a tyto hodnoty vydělíme n. Průměrné výšky si setřídíme a označíme jako X1, X2, … ,X(R-r+1)(S-s+1). Zároveň zvolíme X0 = 0.
| k |
| j=1 |
| k |
| j=1 |
- Do intervalových stromů přidáme všechna políčka, jejichž hodnota je v intervalu <Xi-1, Xi).
- Ze stromu S získáme hodnotu k pro obdélník patřící k Xi.
- Ze stromu T získáme hodnotu ∑
pj pro obdélník patřící k Xi.k j=1
A to je celé. Do každého intervalového stromu vložíme každou z N hodnot maximálně jednou, tedy dostáváme časovou složitost O(RS · log R · log S). Hodnoty výšek a průměrů máme setříděné a zpracováváme je ve vzestupném pořadí.
Posíláme gratulaci Michalu Punčochářovi, který tuto úlohu jako jediný vyřešil optimálně a zcela správně.
26-4-6 Sněhová bitva (Zadání)
Nejjednodušší řešení by bylo nepředpočítávat si vůbec nic. Při dotazu, zda na polopřímce AB→ je ještě nějaký další bod, jednoduše spočítáme směr z bodu A do všech ostatních a porovnáme se směrem do B. Jak spočítat a reprezentovat směr rozebereme níže, prozatím předpokládejme, že jde směr spočítat i porovnat v konstantním čase. Takové řešení má dotaz za O(n) a potřebuje O(n) paměti na uložení vstupu. Ale za takto jednoduchou úlohu by asi organizátoři 11 bodů nenabízeli.
Tak co bychom si mohli předpočítat? Co třeba odpověď na každý možný dotaz? Protože odpověď na takový dotaz je jen ano/ne a počet dvojic je O(n2), bude nám stačit dvourozměrné pole. Ale předpočítat si ho pomocí výše zmíněného jednoduchého řešení by trvalo O(n3). To zkusíme zrychlit.

Zkusme si spočítat naráz všechny odpovědi pro jednoho mířícího bojovníka A a všechny možné cíle C. Tedy odpovědi pro všechny polopřímky AX→. Uděláme to tak, že spočítáme směry pro všechny cíle a tyto směry setřídíme. Tím se nám stejné směry „sesypou“ k sobě. Nyní můžeme směry ještě jednou projít a najít úseky stejných směrů a jim odpovídající cíle označit, že leží na společné polopřímce, a tedy že pro ně bude odpověď ano. Toto nám zabere O(n· log n) pro jednoho mířícího bojovníka, tedy O(n2· log n) celkem. Spotřebujeme O(n2) paměti a odpovídat můžeme v konstantním čase.
Nyní, co s tím směrem? Nejpřirozenější reprezentace by asi byla počítat úhel. To s sebou ale nese jisté technické problémy (jako například trochu pomalejší výpočet trigonometrických funkcí či chlupatá iracionální čísla, co se kamarádí s π i pro rozumná vstupní data). Budeme tedy počítat poměr rozdílu v ose X a Y. To má stále jisté problémy. Jednak tento poměr bude pro protilehlé směry vycházet stejně – směr doleva dolů a směr doprava nahoru bychom nerozlišili. Tedy, směr bude dvousložková hodnota. První složka bude říkat, jestli je to směr nahoru, nebo dolů (resp. doleva, či doprava v případě vodorovných směrů, ať se vyhneme kladné a záporné nule). Druhým problémem je dělení nulou pro svislé směry. Ale v takovém případě si budeme nějakým způsobem reprezentovat nekonečno (např. čísla s plovoucí čárkou opravdu mají speciální hodnotu pro nekonečno).
Nakonec jedna poznámka o tom, že to může jít lépe. Pokud bychom použili hešování místo třídění pro shluknutí stejných směrů dohromady, dostali bychom se na očekávanou složitost O(n) (bohužel jen očekávanou, ne nejhorší případ) pro jednoho střelce, namísto O(n· log n). To lze udělat proto, že nám vlastně vůbec nezáleží na pořadí, v jakém směry dostáváme, jen aby byly ty stejné pohromadě.
To má ale háček. Čísla s plovoucí čárkou mají v počítači tendenci akumulovat při operacích chybu. Proto je třeba je porovnávat s malou tolerancí, nikoliv na přesnou rovnost, a to s hešovací tabulkou nejde. Pokud bychom ale měli celočíselný (nebo alespoň racionální) vstup, můžeme směr ukládat jako zlomky a poté nám již hešovací tabulka pomůže. Ale převést zlomek na základní tvar nezvládneme v konstantním čase. Všimneme si však, že když jsou čísla na vstupu omezená hodnotou L, dva různé zlomky se budou lišit alespoň o 1 / L2. Vynásobíme tedy všechny směry L2 a budeme dělit celočíselně.
26-4-7 Královští špioni (Zadání)
Rozplést síť špionů většinou nebývá snadné. V této úloze jsme ji ale měli již pěkně naservírovanou.
Nejjednodušším, avšak pomalým řešením je odsimulovat putování zpráv postupně
od každého špiona. K tomu nám stačí si vstup načíst do pole A. Pak už jen
v jedné proměnné udržujeme počet kroků a ve druhé pozici zprávy, tj. číslo
špiona, u kterého se zrovna nachází. Jedno přeposlání zprávy provedeme snadno
přiřazením pozice = A[pozice].
Jak poznáme, kdy se má předávání zpráv zastavit? Jednoduše si budeme v dalším poli pamatovat, kteří špioni tuto zprávu viděli. Uvedené řešení má časovou složitost O(N2), kde N je počet špionů. Za takové CodEx uděloval tři body.
Problém s pomalostí spočívá v tom, že procházíme v síti špionů stále dokola ta stejná místa, přestože výsledek je vždy stejný. Při každém průchodu můžeme rovnou uložit počty kroků pro všechny špiony, přes které jsme zprávu posílali.
Všimněme si, že každá zpráva končí své putování nějakým cyklem – částí, ve které si špioni posílají informace v kruhu. Zpráva vyslaná libovolným špionem na cyklu bude předaná přesně tolikrát, kolik je v daném cyklu špionů. V úseku před cyklem roste doba putování postupně o jedna za každého špiona.
Asymptoticky jsme si zatím nepomohli. Nic nám totiž nezaručuje, že špiony budeme procházet ve správném pořadí od toho nejvzdálenějšího. Musíme začít využívat to, co jsme již spočítali. Když při simulaci dojdeme ke špionovi, pro nějž máme výsledek spočítaný, nebudeme pokračovat dál, protože bychom se stejně nic nového nedozvěděli. K počtu kroků jen přičteme výsledek pro aktuálního špiona.
Tím už pro každého špiona provedeme jenom konstantně mnoho operací. Celková časová složitost tak je O(N). Pro úplnost ještě dodejme, že s použitý trikem se můžeme setkat častěji. Dokonce si vysloužil vlastní název memoizace.

26-4-8 Dlaždičky (Zadání)
Úkol 1 – Počet jedniček dělitelný třemi
K řešení prvního úkolu nám bude stačit poměrně jednoduchá myšlenka. Budeme si zleva doprava propagovat dosavadní počet jedniček modulo 3 (úplně stejný trik bychom mohli použít pro libovolnou jinou konstantu).
Dlaždice si pořídíme dvojího typu, jedny budou mít nahoře nulu, druhé jedničku. Ty s nulou předávají stejnou hodnotu, tedy mají levou i pravou stranu obarvenou stejně. Naopak ty s jedničkou předávaný počet zvyšují, takže mají vlevo x a vpravo (x + 1) mod 3. Dole všechny dlaždice obarvíme barvou D. Naše dlaždice tedy vypadají takto:
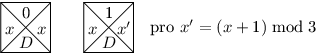
Dolnímu okraji přidělíme barvu D, levému i pravému okraji pak barvu 0.
Pro vstup, který má počet jedniček dělitelný třemi, určitě umíme dláždění vytvořit (přesně podle myšlenky řešení jen počítáme jedničky ve vstupu modulo 3).
Dláždění buď vůbec nelze vytvořit, nebo je určené jednoznačně. Pro daný vstup máme právě jednu možnost, jakou dlaždici přiložit přímo k levému okraji, pak právě jednu možnost, jakou dlaždicí navázat na tuto první atd. Dláždění tak vždy počítá jedničky modulo 3, tedy pokud dláždění existuje, vstup skutečně podmínku splňoval.
Všimněte si, že máme levý i pravý okraj zdi obarvený stejnou barvou. Tím jsme si ušetřili řešení okrajových případů. Chceme-li ovšem takový trik provést, musíme si velmi dobře rozmyslet, jestli si tím nepokazíme správnost. Obecně tím totiž tvrdíme, že zřetězíme-li několik vstupů splňujících naši podmínku, výsledek ji bude splňovat také.
Úkol 2 – Snižování výšky dláždění o konstantu
Představme si, že máme dláždění výšky t, a podívejme se na libovolný sloupec tohoto dláždění. Obarvení horizontálních stran dlaždic, vyjma horní stěny nejvyšší a spodní stěny nejnižší dlaždice, nemá pro zbytek dláždění žádný význam, určuje pouze návaznosti v tomto sloupci.
Naopak obarvení vertikálních stran důležité je, a to po celé výšce sloupce, určuje totiž návaznosti v rámci jednotlivých řádků. Toto obarvení tedy chceme zachovat.
Abychom snížili výšku dláždění, nahradíme každý sloupec jedinou dlaždicí. Očíslujme si dlaždice ve sloupci od 0 do t-1 (dlaždice v nultém řádku přiléhají ke vstupu), obarvení každé z nich pak (ℓi, hi, pi, di). Nová dlaždice pak bude nahoře obarvena barvou h0, dole barvou dt-1. Pro boční stěny zavedeme nové barvy, které označíme jako uspořádanou t-tici (ℓ0, … , ℓt-1), resp. (p0, … , pt-1).
Pro úplnost dodejme, že levý okraj přebarvíme z barvy ℓ na (ℓ, … , ℓ), podobně pravý.
Sloupce k sobě přiléhají stále stejně, ovšem výšku dláždění jsme z t zmenšili na 1. Velikost množiny D, tedy množiny všech použitelných dlaždic, nepovažujeme za důležitou, přesto stojí za zmínku, že jsme ji tímto trikem exponenciálně zvětšili.
Úkol 3 – Dlaždičkové závorkování
Kdybychom chtěli správnost závorkování ověřovat přímočaře, mohli bychom postupně
umazávat dvojice (), které určitě správně jsou. Místo opravdového smazání
takových dvojic a následného posouvání zbytku řetězce se hodí „smazané“
závorky jen něčím nahradit a vstup nechávat na původním místě.
Potřebujeme tedy vždy nahradit dvě závorky (), mezi kterými buď není vůbec nic,
nebo jsou pouze smazané znaky. Ostatní závorky musíme poslat o řádek níž, na
konci chceme mít smazaný celý vstup. Toho můžeme dosáhnout například
s následující sadou dlaždiček:

␣.
V nejhorším případě budeme ovšem potřebovat n/2 kroků na smazání celého vstupu, program tedy pracuje v lineární časové složitosti. To přece musí jít lépe!
Závorkování rychleji
Abychom dosáhli lepší než lineární složitosti, vypůjčíme si trik z řešení 26-1-8. Budeme počítat úroveň zanoření, neboli kolik jsme zatím potkali neuzavřených závorek. A protože máme jen konečnou množinu barev, budeme si tuto úroveň ukládat jako číslo ve dvojkovém zápisu.
Úroveň zanoření může být u správného závorkování nejvýše n/2, na reprezentaci takového čísla ve dvojkovém zápisu potřebujeme log n bitů. My si dvojkové zápisy budeme ještě doplňovat tak, aby vždy začínaly nulou, ale tím jsme přidali jeden řádek. Náš program tak bude pracovat v logaritmické časové složitosti.
Vždy, když potkáme otvírací závorku, úroveň vnoření o 1 zvýšíme, u zavíracích závorek ji zase o 1 snížíme. Zápis úrovně nám bude vznikat směrem dolů, jinak řečeno, při hotovém dláždění ho můžeme číst na pravých stranách dlaždic v daném sloupci. Navíc si nepořídíme dlaždice, které by uměly reprezentovat odečítání do záporných čísel.
Horizontálně si budeme předávat hodnoty jednotlivých bitů čísla, vertikálně přenos mezi těmito bity. Ještě si dovolíme jeden podlý trik, a to ten, že vertikální přenosy budeme kódovat opět závorkami. Díky tomu totiž nemusíme nijak odlišovat přikládání dlaždic ke vstupu a k předchozímu řádku dláždění.
Pro úplnost dodejme, že všechny tři okraje zdi obarvíme 0, a pak se konečně pojďme podívat na používané dlaždice:

Úkol 4 – Minimální složitost závorkování
Zkusme si pořídit různé posloupnosti závorek délky n. Řekněme, že budeme
posloupnosti budovat z dvojic závorek, že nejprve vybudujeme první polovinu
této posloupnosti a že v první polovině smíme použít pouze dvojice () a ((.
Takto jistě můžeme vytvořit n / 4 posloupností délky n / 2
takových, že žádné dvě nemají stejný počet otevřených závorek. Nyní každou
z nich doplňme pomocí dvojic () a )) na správně uzávorkovanou posloupnost
délky n.
Pojďme se teď podívat na dláždění, která pro jednotlivé posloupnosti vzniknou. Na chvilku předpokládejme, že každé z nich má výšku právě V.
Pro n / 4 prvních polovin máme n / 4 druhých polovin, přičemž první polovině vždy odpovídá právě jedna ze druhých polovin. Na prostředním sloupci dláždění tedy musíme být schopní odlišit alespoň těchto n / 4 různých možností, jinými slovy musí existovat n / 4 možných obarvení prostředního sloupce.
Pokud označíme celkový počet barev v našem programu jako B, můžeme možná obarvení prostředního sloupce omezit také výrazem BV. Tím dostáváme nerovnost BV ≥ n / 4, úpravami získáme V ≥ logB n - logB 4. To ovšem můžeme asymptoticky zapsat jako V ∈Ω(log n).
Rozhodnout správné závorkování tedy skutečně neumíme lépe než logaritmicky.
Pro úplnost ještě okomentujme náš drzý předpoklad, že dláždění pro každou z našich posloupností mělo výšku právě V. To samozřejmě nemusí být pravda, některá klidně mohla být jednořádková. Každé dláždění, které má výšku maximálně V ovšem umíme „nafouknout“ tak, aby mělo výšku právě V. Můžete si jako cvičení rozmyslet, jak toho dosáhnout.

Úkol 5 – Ekvivalence s Turingovými stroji
Začněme s asi snazším převodem, a to z dlaždičkových programů na Turingovy stroje. Necháme Turingův stroj simulovat stavbu dláždění, a to konkrétně po řádcích. Obarvení vodorovných hran budeme považovat za znaky na pásce vždy před provedením kroku a po něm, obarvení svislých hran pak za stavy.
Pro každou dlaždici (ℓ, h, p, d) tedy zavedeme pravidlo typu (ℓ, h) →(p, d, →). Tedy pokud se ve stavu ℓ na pásce nachází znak h, stroj zapíše znak d a přejde do stavu p, hlava se posune doprava.
Tímto umíme vybudovat jeden řádek dláždění. Řádků ale může být víc, potřebujeme se tedy umět vracet zpět. V případě, že aktuální stav odpovídá barvě pravého okraje zdi, řekněme P, a na vstupu se nachází mezera, přejde stroj do speciálního návratového stavu. V něm znaky vždy zapisuje zpět a posouvá se doleva, dokud opět nenarazí na mezeru.
Návrat nastartuje pravidlo (P, ␣) →(N, ␣, ←), během
vracení potřebujeme pravidla typu (N, x) →(N, x, ←) pro
všechna možná obarvení x a k ukončení návratu přidáme ještě pravidlo (N,
␣) →(L, ␣, →).
Ještě musíme poznat, že je celé dláždění dokončené. Mohli bychom při návratu odlišovat dva stavy: jeden, kdy jsme dosud ze vstupu četli pouze znak odpovídající obarvení dolního okraje, a druhý, kdy se alespoň jeden znak lišil. My si ale představíme, že ve speciálním stavu vybudujeme ještě jeden řádek navíc.
Po skončení návratu umožníme přechod do speciálního stavu, (N, ␣)
→(*, ␣, →). V tomto stavu přijímáme pouze správný znak
(tedy správné obarvení), a pouze pokud dojdeme až na konec vstupu, ukončíme
výpočet. Zavedeme proto ještě dvě pravidla, (*, D) →(*, D,
→) a (*, ␣) →ano.
Už víme, že dlaždičkové programy nejsou silnější než Turingovy stroje. Pojďme teď převést Turingův stroj na dlaždičkový program.
Tentokrát bude jeden řádek dláždění odpovídat jednomu kroku Turingova stroje. Musíme vědět, nad kterým znakem se právě nachází hlava a v kterém stavu se nachází celý stroj. Zároveň nám informaci o stavu stačí znát u znaku pod hlavou, ostatní znaky stejně výpočet ovlivnit nemohou.
Pro každé pravidlo typu (si, zi) →(sj, zj, •) si pořídíme následující dlaždici:
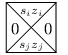
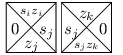
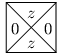
Koncového stavu dosáhneme při čtení nějakého konkrétního znaku, ale aby šlo
dláždění dokončit, musí být správnou barvou obarvený celý poslední řádek. Pro
jakékoli pravidlo typu (s, z) →ano proto přidáme dlaždici (ano,
(s, z), ano, ano) a pro ostatní prvky abecedy dlaždice (ano, z, ano, ano).
Pouze pro okrajové mezery musí dlaždice vypadat jinak, (L, ␣, ano, ano),
analogicky pro pravou stranu.
Zbývá si ještě rozmyslet, jak by měl vypadat začátek dláždění. Potřebujeme do vstupu dostat informaci o počátečním umístění hlavy a počátečním stavu. K tomu si zavedeme ještě jeden speciální inicializační stav. Pak nám budou stačit tyto dlaždice:
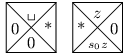
Tím je převod hotov, Turingův stroj umíme simulovat pomocí dlaždičkových programů, tedy tyto dva výpočetní modely jsou skutečně ekvivalentní.