Druhá série třicátého čtvrtého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 34-2-1: Skupinová jízdenka
- 34-2-2: Lezení
- 34-2-3: Na Hroších pláních
- 34-2-4: Brněnská procházka
- 34-2-S: Manimujeme – skupiny, transformace a updatery
- 34-2-X1: Převod čísel
 34-2-1 Skupinová jízdenka (Zadání)
34-2-1 Skupinová jízdenka (Zadání)
Označme r cenu jednotlivého jízdného a s cenu skupinového jízdného. Potom cena, kterou Alice a Bob zaplatí, pokud se setkají v nějakém vrcholu M, je rovna s ·d(M, C) + r ·d(A, M) + r ·d(B, M), kde d(M, C) značí vzdálenost mezi vrcholy M a C, tedy délku nejkratší cesty mezi nimi. A podobně pro ostatní vrcholy. To platí, jelikož se jedná o součet cen, jak se do vrcholu dostat z A a B, a ceny, jak se společně dostat do C.
Spuštěním Dijkstrova algoritmu z města C jsme schopni pro každý vrchol M zjistit vzdálenost d(C, M). Pokud tuto vzdálenost vynásobíme s, dostáváme cenu, za kterou se Alice s Bobem dostanou z M do C. Podobně můžeme pomocí Dijkstrova algoritmu puštěného z bodu A získat vzdálenost d(A, M) a následným vynásobením r minimální cenu z A do M. Stejně tak spuštěním z B získáme vzdálenost d(B, M) a z ní cenu r ·d(B, M).
Nyní v každém vrcholu známe cenu, za jakou se do něj umí dostat Alice, za jakou se do něj umí dostat Bob, a kolik je bude stát se společně dopravit do Chebu. Pokud tyto hodnoty sečteme, dostaneme celkovou cenu výletu, pokud by se setkali ve vrcholu M. Jelikož se mohou setkat v kterémkoliv vrcholu a nás zajímá nejnižší cena výletu, vybereme z těchto součtů ten minimální.
Časově nejnáročnější operací je Dijkstrův algoritmus. Pokud bychom použili přímočarou implementaci, bude celková časová složitost O(n2). Můžeme ale použít binární haldu a tím Dijkstrův algoritmus zrychlit na O((m + n) log n). Prostorová složitost je O(n+m).
 34-2-2 Lezení (Zadání)
34-2-2 Lezení (Zadání)
Úloha má několik různých přístupů, kterými se dá dosáhnout rychlého řešení, my si ukážeme hladový algoritmus.
Označme si celkový počet trestných bodů i-tého lezce Si, počet trestných bodů za první dvě disciplíny Ai (to je součin pořadí v prvních dvou disciplínách, který umíme spočítat) a hypotetické pořadí v lezení na obtížnost jako Bi (tedy Si = AiBi). Náš lezec bude ten s indexem 0.
My nyní hledáme nejhorší možné pořadí lezce 0, tedy největší k+1 takové, že k lezců mělo nižší počet trestných bodů než náš lezec. Nyní se podívejme, za jakých podmínek může i-tý lezec porazit lezce 0:
| Si | < S0 | ||
| AiBi | < A0B0 | ||
| Bi | <
|
Všechny hodnoty na pravé straně známe (A máme spočtená a B0=1). Pro každého lezce tak umíme spočítat, kolikátý nejhůře může skončit, aby porazil našeho lezce. Označme toto pořadí Pi.
To již vede na hladové řešení. Pro každé pořadí v poslední disciplíně B > 1 najdeme ty lezce, pro které platí B ≤ Pi. Z těchto lezců přidělíme pořadí B tomu s minimálním Pi. Přidělování pořadí umíme provést rychle, pokud si lezce setřídíme vzestupně podle Pi. Pak stačí jeden sekvenční průchod tímto polem: pokud podmínka B ≤ Pi platí, danému lezci můžeme rovnou přidělit pořadí B, protože lezci po něm mají vyšší Pi nebo stejné. V opačném případě víme, že lezce již nemůžeme umístit tak, aby našeho porazil, můžeme jej tedy umístit na nejhorší možnou pozici, aniž bychom cokoliv pokazili.
Tím zjistíme počet lezců, kteří toho našeho překonali. Jako výsledek vrátíme tuto hodnotu + 1.
Jelikož třídíme hodnoty v rozsahu 1 až n2, můžeme si je představit jako čísla o základu n, která mají nejvýše dvě cifry. Ta pak můžeme třídit pomocí radix-sortu v lineárním čase vzhledem k n. Zbytek algoritmu jsou jen sekvenční průchody, proto je celková časová složitost O(n) (stejně tak paměťová).
Zbývá ještě ukázat, že hladový algoritmus skutečně funguje. Pořadí lezců, které najde, určitě může nastat. Potřebujeme ale ukázat, že více lezců už toho našeho porazit nemůže.
To nahlédněme sporem. Uvažme nějaké uspořádání v poslední disciplíně takové, že l > k lezců bude mít nižší skóre než náš lezec. BÚNO předpokládejme, že ti lezci, kteří jej porazí, se nachází na pozicích 2 až l+1. Kdyby ne, můžeme je na tyto pozice umístit a jejich skóre jen zlepšit.
Nyní se zaměřme na první místo, kde se toto uspořádání liší od toho, které generuje náš algoritmus. Uvědomme si, že lezec, kterého na toto místo přiřadil náš algoritmus, je v údajně lepší posloupnosti buď později, anebo není mezi l nejlepšími. V obou případech však můžeme dané lezce prohodit a nic se tím nepokazí.
Takto můžeme induktivně upravovat, až první místo, kde se posloupnosti budou lišit, je (k+2)-té místo, kde má být v údajně lepší posloupnosti lezec, který stále toho našeho porazí. To ale není možné, jelikož žádný takový nezbyl. Jelikož jsme sadou úprav, kterými jsme nic nemohli pokazit, dospěli k něčemu, co zjevně nemůže existovat, nemůže existovat ani žádné uspořádání lepší než to, které našel hladový algoritmus.
To ale znamená, že hladový přístup je korektní.
 34-2-3 Na Hroších pláních (Zadání)
34-2-3 Na Hroších pláních (Zadání)
Na vstupu jsme dostali dva claimy ve tvaru mnohoúhelníka. Hranice každého claimu je tvořena lomenou čárou, což je posloupnost hran (úseček) napojených ve vrcholech (bodech).
Abychom si úvahy zjednodušili, předpokládejme, že žádné dva vrcholy nemají stejnou y-ovou souřadnici. Tím pádem žádná hrana claimu není vodorovná. Později dořešíme, co si počít, když to vstup nesplňuje.
Také si všimneme, že existují dva způsoby, jak mohou mít dva claimy společný bod: buďto se protnou jejich hranice (to jsou nějaké lomené čáry), nebo leží jeden claim celý uvnitř druhého.
První případ poznáme podle průsečíků hran claimů. Druhý tak, že jeden (pevně zvolený) z vrcholů claimu leží uvnitř druhého claimu. To někdy nastane i v prvním případě, ale to nám nevadí, tak jako tak je to společný bod.
Vrchol uvnitř druhého claimu
Pro každý claim A zvolíme nějaký jeho vrchol x a otestujeme, zda leží uvnitř druhého claimu B. Vedeme z x polopřímku libovolným směrem a počítáme, kolik hran claimu B protne: pokud sudý počet, je x venku, jinak uvnitř.
Pokud se polopřímka strefí do vrcholu claimu B, podíváme se na sousední vrcholy. Pokud oba leží na různých stranách polopřímky, zjevně jsme proťali hranici claimu, takže to počítáme jako 1 průsečík. Pokud oba leží na stejných stranách, tak jsme o hranici jen „zavadili“, tudíž to počitat nechceme.
Ještě větší komplikace nastane, pokud nějaká hrana, nebo dokonce posloupnost několika po sobě jdoucích hran, leží přímo v polopřímce. Tehdy se podíváme na vrcholy těsně před touto posloupností a těsně za ní a provedeme stejnou úvahu jako při strefení se do vrcholu.
Tato část algoritmu běží v lineárním čase.
Průsečíky hran
Průsečíky hran budeme hledat zametáním roviny. Budeme posouvat vodorovnou přímku (koště) shora dolů a sledovat, jak se protíná se zadanými claimy (mnohoúhelníky). Budeme si udržovat průřez – seznam hran claimu proťatých koštětem, seřazený tak, aby průsečíky s koštětem šly zleva doprava.
Všimneme si, že než se nějaké dvě hrany protnou, musí se nutně v průřezu stát sousedními. Stačí tedy pokaždé, když upravíme průřez, zjistit, jaké dvojice hran se staly sousedními, a pro ně otestovat, zda se někde pod koštětem protnou.
Koštětem není potřeba pohybovat spojitě – zajímavé věci se dějí jenom tehdy, projde-li koště vrcholem claimu. Proto si seřadíme vrcholy shora dolů a budeme koštětem „skákat“ po jejich y-ových souřadnicích. U každého vrcholu si také zapamatujeme, ke kterému claimu patří a které dvě hrany se v něm potkávají.
Konvexní případ
Pro konvexní claimy je zametání jednoduché.
Představme si jeden konvexní claim s vrcholy v obecné poloze. Claim má jednoznačně určený nejvyšší a nejnižší bod. V těchto bodech můžeme okraj claimu rozdělit na levou a pravou část.
Při zametání claimu narazí koště nejprve na nejvyšší bod, pak bude nějakou dobu průřez obsahovat jednu hranu z levého okraje a jednu z pravého, až nakonec koště v nejnižším bodě claim opustí. Údržba průřezu tedy bude jednoduchá: v nejvyšším bodě přidáme nejvyšší dvě hrany. Pak v každém vrcholu jedna hrana skončí a druhá začne, takže z průřezu jednu odstraníme a druhou přidáme. Nakonec v nejnižším bodě zrušíme obě hrany.
Nyní si představíme, že zametáme dva claimy současně a udržujeme společný průřez. Vkládání a mazání hran provádíme pro každý claim zvlášť, jak jsme popsali. Ale kdykoliv se stanou sousedními dvě hrany z různých claimů, podíváme se, zda se neprotínají.
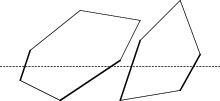
Celkem navštívíme O(n) vrcholů. Jelikož průřez vždy obsahuje nejvýše 4 hrany, zvládneme každý vrchol obsloužit v konstantním čase. Nesmíme ovšem zapomenout na počáteční seřazení vrcholů shora dolů, takže celý algoritmus trvá O(n log n).
Implementaci nám může zjednodušit, že v průřezu musí obě hrany jednoho claimu vždy sousedit. V opačném případě jsme už dříve museli objevit průsečík.
Nekonvexní případ
Zametání nekonvexních claimů je trochu složitější. Průřez může obsahovat libovolný sudý počet hran jednoho claimu. Podíváme se, co se může s průřezem stát, narazíme-li na vrchol claimu, kde se potkávají nějaké dvě hrany:
- Obě hrany pokračují dolů – tehdy jsme na „špičce“ claimu, takže přidáme obě hrany do průřezu.
- Obě hrany pokračují nahoru – obě hrany skončily a z průřezu je smažeme.
- Jedna hrana vede nahoru, druhá dolů – horní hranu odstraníme, dolní přidáme.

Pokud přidáme hranu, musíme najít její sousedy a ověřit, jestli se s nimi neprotíná. Podobně pokud hranu smažeme, stala se předchozí hrana sousedem následující, takže ověřujeme jejich průsečík.
Potřebujeme najít datovou strukturu, ve které si budeme průřez pamatovat, abychom všechny tyto operace uměli provádět rychle. Potřebujeme umět vložit novou hranu na správné místo, smazat hranu a zjistit předchůdce a následníka hrany. To zajistí vyhledávací strom v čase O(log n) na operaci. Jenže ve vrcholech vyhledávacího stromu si nemůžeme pamatovat x-ové souřadnice průsečíků hran s koštětem – ty se každým posunutím koštěte změní. Pořadí hran se nicméně nemění (zatím se žádné dvě hrany neproťaly), takže pro každé dvě hrany je jednoznačně určeno, která z nich je nalevo a která napravo. Do vrcholů stromu tedy uložíme přímo hrany.
Algoritmus celkem zpracuje n vrcholů, v každém z nich provede konstantně mnoho přidání/smazání hran v průřezu. To pokaždé vyvolá O(1) operací se stromem, z nichž každá stojí O(log n). Celkem tedy algoritmus pracuje v čase O(n log n).
Obecná poloha
Zbývá dořešit, co si počít, pokud dva body mají stejnou y-ovou souřadnici. (Rozmyslete si, kde jsme tento předpoklad vlastně potřebovali.)
Pomůže obvyklý trik: představíme si, že celou rovinu otočíme okolo libovolného bodu o velmi malý úhel po směru hodinových ručiček. Tím se v každé dvojici se stejnou y-ovou souřadnicí posune levý bod nad pravý. A pokud byl předtím nějaký bod nad jiným, tento vztah bude při dostatečně malém otočení zachován.
Takové otočení je ovšem ekvivalentní s tím, že body nesetřídíme jenom podle y-ové souřadnice, nýbrž lexikograficky primárně podle y, sekundárně podle x. Zbytek algoritmu není potřeba měnit.
 34-2-4 Brněnská procházka (Zadání)
34-2-4 Brněnská procházka (Zadání)
Zadaná úloha byla hledáním nejdelší vážené indukované cesty na zadaném grafu. Nalezení nejdelší indukované cesty je NP-těžký problém pro obecné neohodnocené grafy. Náš graf ale není neohodnocený, a už vůbec není obecný – jde o skoro rovinný graf, ostatně vzniknul z cest v Brně a okolí.
Bohužel vám ale efektivní algoritmus pro nalezení optimální cesty nedáme, protože ho neznáme, pokud vůbec existuje. Místo toho vám představíme vybraná řešení organizátorů, kteří úlohu řešili spolu s vámi.
Řešení Jirky Sejkory
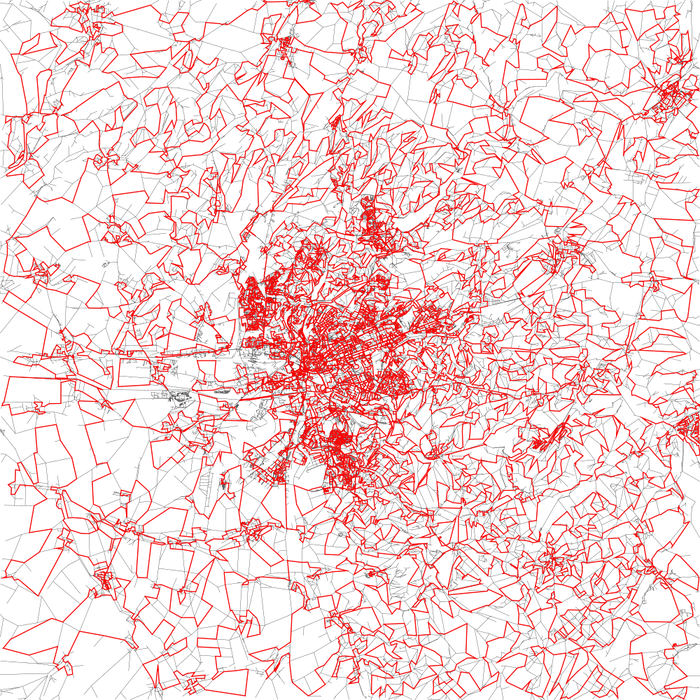
Mé řešení pracuje ve dvou fázích. V první fázi najde nějakou počáteční cestu, které je alespoň trochu dobrá, ale ne moc dobrá. V druhé fázi pak tuto cestu vylepšuje.
První cestu nalézám opakovaným náhodným výběrem počátečního bodu a poté náhodným prodlužováním cesty, dokud to jde. Jakmile dojdeme do slepé uličky, tak skončíme a máme naši cestu. Tento postup velmi rychle končí ve slepých uličkách, takže toto několikrát opakuji (tisíce pokusů) a pamatuji si nejdelší cestu, kterou jsem našel. Pro drobné vylepšení vybírám následující vrchol vážený počtem vrcholů, které jsou z něj ještě dostupné. Tohle by šlo výrazně zlepšit (všimněte si, že nikdy nebacktrackuji), ale mým cílem je zde najít nějakou cestu, ne nutně příliš dobrou.
Vylepšování cesty je ta mnohem zajímavější část. Nalezenou cestu vylepšíme tak, že někde odstraníme souvislý úsek cesty délky N, a najdeme pomocí DFS co nejdelší validní smyčku, která zase cestu spojí. Tím jsme problém převedli zase na hledání nejdelší cesty v nějakém obřím grafu (jde o strom všech validních cest, exponenciálně větší než zadaný graf). Přidáme proto omezení na hloubku prohledávání, a díky tomu najdeme nejdelší cestu, která používá maximálně K hran. Při prohledávání jsem používal K v rozsahu od 16 (první vylepšení) do 26 (když už byl graf skoro plný).
Délky vyříznutých úseků N jsem používal 2, 4, 6, 10, 20, 50. Ty nejdelší úseky byly jen zřídka k něčemu užitečné, jelikož je muselo nahradit málo dlouhých hran, a to je v grafu vzácné. Vždy jsem v náhodném pořadí vyzkoušel všechny vyříznuté úseky (těch je lineárně s aktuální délkou cesty).
Nevýhodou tohoto přístupu je, že není možné posunout počáteční a koncový bod cesty. Jsme proto do jisté míry vázáni na počáteční řešení.
Tento algoritmus dobíhá do jednotek minut. Je ovšem možné vícekrát opakovat různé délky a také hledat vylepšení, které používá více hran, což běh algoritmu výrazně prodlužuje. Nalezená řešení byla dlouhá kolem 3300 kilometrů, i při opakovaném spouštění se délka výrazně nelišila.
Řešení Kuby Pelce
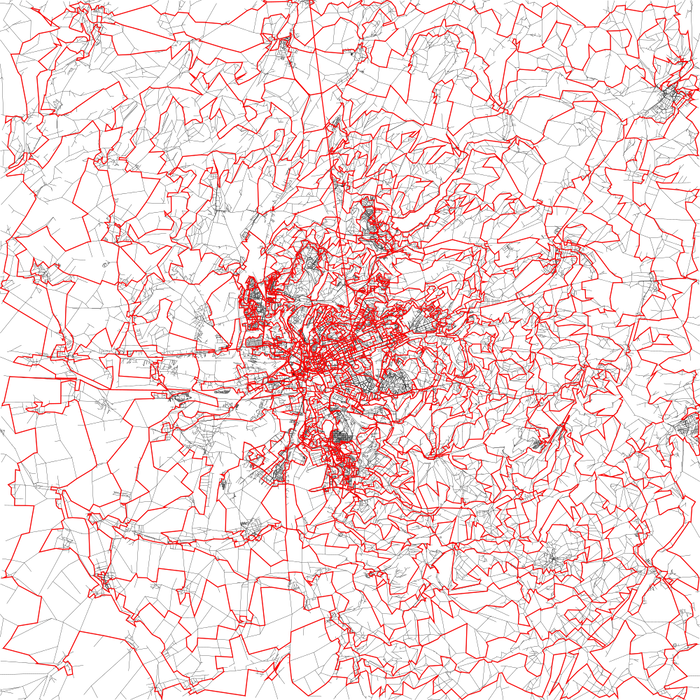
Mé řešení je založené na myšlence vést cestu spirálovitě od krajů mapy do středu. Nejdelší cestu budu hledat prohledáváním do hloubky (dále DFS). Začnu v nejzápadnějším vrcholu mapy a v každém vrcholu se pokusím jít tou nejlevější možnou cestou vzhledem ke směru, ze kterého jsem do vrcholu přišel. K určení směrů využívám GPS souřadnice ve vstupu. Jelikož se jedná o DFS, pokud se někdy dostanu do vrcholu, ze kterého v cestě nemůžu validně pokračovat, prostě se vrátím o vrchol zpět a půjdu druhou nejlevější cestou, a tak dále.
Pokud bych použil neupravené DFS, tak by tento algoritmus vlastně zkusil najít všechny možné cesty začínající v nejzápadnějším vrcholu, a to by trvalo extrémně dlouho. Proto používám několik heuristik.
Ještě před spuštěním algoritmu v grafu najdu všechny mosty (takové hrany, jejichž odstraněním se graf rozpadne na dvě jinak nepropojené části – komponenty), odstraním je z grafu, najdu největší vzniklou komponentu a algorimus spustím jen na ní. Při hledání nejdelší cesty je poměrně zbytečné chodit přes mosty, protože cesta se poté už nemůže vrátit zpět. V reálném městě se slepé cesty příliš nevyskytují, a pokud ano, tak jsou tak krátké, že jejich vynecháním si moc neuškodíme.
I když během běhu algoritmu vypisuji každou dosavadní nejdelší cestu, DFS se často dostává do míst grafu, kde zbytečně zkouší mnoho různých zakončení cesty, která nikdy nepovedou k lepšímu výsledku, protože algoritmus v nějakém vrcholu „špatně zabočil“ do slepého místa grafu, a trvá dlouho, než by se DFS opět propracovalo zásobníkem k onomu vrcholu. A to i přes odstranění mostů. Celkově se dá říct, že DFS trvá moc dlouho vracet se v zásobníku zpět. Tak mu trochu pomůžeme.
Pokud algoritmus nějaký počet iterací, třeba milion, nenajde novou nejlepší cestu, usoudíme, že je v nějaké „slepé uličce“ a z vrcholu zásobníku odstraníme několik položek. Pokud po dalším milionu iterací stále nenajde nic lepšího, odstraníme větší část zásobníku, a tak dále. Zahazováním kusů zásobníku samozřejmě odignorujeme mnoho různých cest, potenciálně těch nejlepších, nicméně v praxi tato heurestika funguje dobře. Algoritmus s ní dokáže najít cesty o délce stovek kilometrů v řádu minut, a poté, když dlouho nenachází nic lepšího, skončí na tom, že si vyprázdní celý zásobník.
I přes občasné mazání zásobníku se může stát následující scénář: algoritmus se dostane do „slepé uličky“, dlouho ji prohledává, po nějakém čase odstraní kus zásobníku a vrátí se před místo, kde do ní zabočil, jenže poté se může opět vrátit do stejné slepé uličky, jen tam dorazí trochu jinou cestou. Poslední heurestika opravuje tento problém. Pro každý vrchol si pamatuju, kolikrát jsem ho navštívil. Pokud tento počet překročí nějakou konstantnu, třeba tisíc, tak už do takového vrcholu algoritmus nikdy nevstoupí.
S těmito heurestikami algoritmus našel spirálu o délce zhruba dva a půl tisíce kilometrů.
Řešení Tomáše Slámy
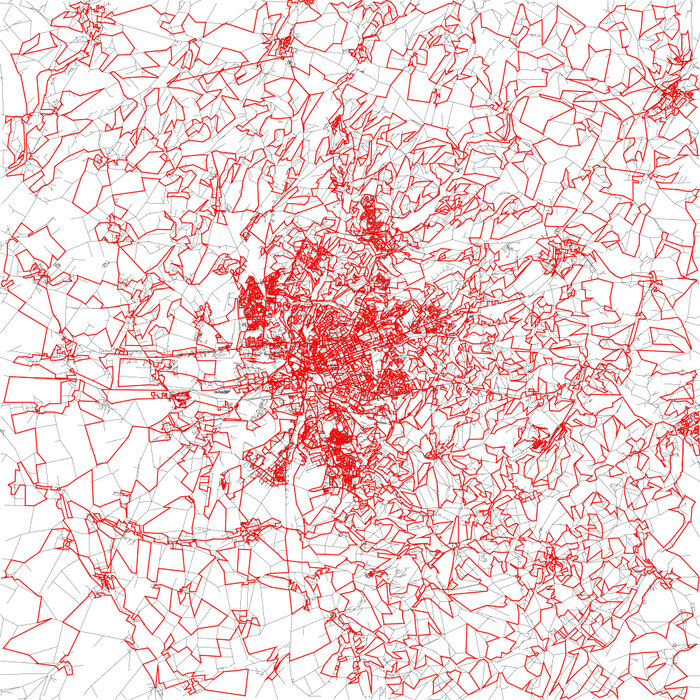
Princip mého řešení je stejný jako řešení Jirky Sejkory – nejprve vygeneruji náhodnou cestu, kterou postupně vylepšuji vysekáváním souvislých úseků vrcholů.
Vysekávání úseku o délce d probíhá sekvenčně: nejprve zkusím
odstranit vrcholy (1, … , d + 1), poté (2, … , d + 2), apod. Pro
každý tento pokus ze startovního vrcholu hledám nejdelší cestu do
koncového vrcholu pomocí DFS (s omezením na počet navštívení vrchlů,
aby algoritmus nehledal do nekonečna). Zde používám zajímavou heuristiku:
v daném vrcholu třídím sousedy podle toho, v jaké vzdálenosti jsou od
koncového vrcholu (v euklidové vzdálenosti – používám zde lat
a lon).
Pro d = {2 … 50, 100, 120, 150} tento algoritmus našel nejdelší cestu dlouhou 3 543 375 metrů.
 34-2-X1 Převod čísel (Zadání)
34-2-X1 Převod čísel (Zadání)
Pro řešení naší úlohy využijeme metody rozděl a panuj. Předpokládejme, že počet cifer zadaného čísla je mocnina dvojky. Tedy N=2M pro celočíselné M. Když tomu tak není, můžeme před zadaný vstup doplnit dostatečné množství nul a tím délku doplnit na nejbližší větší mocninu dvojky. Délka vstupu se tím prodlouží nejvýše na dvojnásobek.
V případě, že na vstupu je jen jedna číslice, je problém triviální. Stačí postupně číslo modulit a dělit B.
V opačném případě si vstupní číslo rozdělíme na poloviny. Jelikož délka původního vstupu byla mocninou dvojky, tak lze vstup rozdělit na dvě stejné části, a dokonce každá z nich bude mít také délku rovnou mocnině dvojky. Na každou z polovin samostatně zavoláme rekurzivně náš algoritmus. Tím získáme dvě čísla v soustavě o základu B, která zbývá spojit dohromady.
Původní číslo X jsme rozdělili na dvě části Y a Z, přičemž platilo X=Y·AN/2 + Z. Převodem čísla do jiné soustavy se ovšem tato rovnost nezměnila. Číslo AN/2 původně mělo hezký zápis (jednička a za ní samé nuly), ale to už v soustavě o základu B neplatí. Je tedy nutné nejprve spočítat AN/2 a pak pomocí aritmetiky v soustavě o základu B spočítat výsledek jako Y·AN/2 + Z.
Potřebné mocniny A si můžeme přepočítat dopředu pro celý algoritmus. Začneme s A a postupně budeme předchozí výsledek umocňovat na druhou (tedy násobit sám se sebou). Stačí nám totiž získat pouze mocniny A, jejichž exponent je mocnina dvojky.
Odhad složitosti
Délka vstupu je N=2M a číslo A lze zapsat v soustavě o základu B do L buněk. Nechť používaný algoritmus na násobení má složitost Θ(Xk) pro násobení čísel délky X.
Na předvýpočet mocnin A budeme potřebovat M-1 násobení. Ovšem budeme násobit čísla délek L, 21L, 22L, …, 2M-2L. Součet délek bude menší než 2M-1L < NL. Časová složitost předvýpočtu bude O((NL)k).
Průběh algoritmu si můžeme představit jako vyvážený binární strom. Kořen reprezentuje převod celého čísla; jeho potomci pak jsou dvě části, na které se dané číslo rozdělilo. Takto to postupuje až do listů, které reprezentují triviální převod jednociferného čísla. Každý list nám trvá O(L) času, celá poslední úroveň stromu tedy O(NL).
Na i-té úrovni stromu (v nulté úrovni je kořen) je 2i vrcholů, každý z nich vyžaduje násobení čísel délky LN / 2i. Celková složitost i-té úrovně tedy je:
Pokud k=1, tak součet přes všech M= log N úrovní, a tedy i celková složitost algoritmu je O(NL· log N).
Pokud však k>1, tak se jedná o součet geometrické řady, a tedy celková složitost se sečte na O((NL)k).
Paměťová složitost algoritmu je O(NL).
Drobné zrychlení na závěr
Pokud je B menší než A, tak můžeme udělat následující trik: Místo toho, abychom převáděli do soustavy o základu B, tak budeme převádět do soustavy o základu Br, kde r je nejmenší možné celé číslo takové, aby bylo Br ≥ A. Při vypisování můžeme snadno výsledek převádět do soustavy o základu B, protože jedna cifra v soustavě o základu Br bude odpovídat r cifrám v soustavě o základu B.
Ovšem čísla do Br se stále vejdou do jedné buňky, protože A2>Br. Jelikož interně v algoritmu bude L=1, celková časová složitost tedy bude O(Nk + LN) a paměťová složitost bude jen O(N).
 34-2-S Manimujeme – skupiny, transformace a updatery (Zadání)
34-2-S Manimujeme – skupiny, transformace a updatery (Zadání)
K letošnímu seriálu nevydáváme řešení v klasické podobně, nicméně můžete se podívat na programy a animace od řešitelů: http://ksp.mff.cuni.cz/viz/34-5-S/komentare