První série třicátého čtvrtého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 34-1-1: Běžkař
- 34-1-2: Líný student
- 34-1-3: Pilný student
- 34-1-4: Sjezdař
- 34-1-S: Manimujeme – úvod
- 34-1-X1: Rostoucí strom (teoretická)
- 34-1-X2: Rostoucí strom (praktická)
 34-1-1 Běžkař (Zadání)
34-1-1 Běžkař (Zadání)
Úlohu budeme řešit pomocí prohledávání stavového prostoru. Všimněme si, že stavů, ve kterých se Kevin může nacházet, není příliš mnoho. Stavy se mohou lišit pouze tím, v jakém vrcholu se Kevin nachází a zda má nasazené běžky.
Sestrojíme si graf, kde vrcholy budou možné stavy a hrana povede mezi dvěma vrcholy právě tehdy, když se dá mezi danými stavy přímo přejít. Ohodnocení hrany bude čas, za jaký je Kevin schopen se mezi stavy přesunout.
Speciálně to znamená:
- Mezi stavy, kdy se Kevin nachází na stejném místě, povede hrana s ohodnocením k. To odpovídá sundání / nandání běžek.
- Mezi stavy sousedních křižovatek, kde má Kevin nasazené běžky, povede hrana s ohodnocením určeným časem, za jaký se Kevin přesune mezi křižovatkami na běžkách.
- Analogicky pro stavy, které jsou sousední a kde má Kevin běžky sundané.
V tomto grafu nyní hledáme nejrychlejší způsob, jak se dostat ze startu do cíle. Jinými slovy hledáme nejkratší cestu v ohodnoceném grafu (s nezápornými ohodnoceními). Tu můžeme nalézt pomocí Dijkstrova algoritmu s haldou, který nám seběhne v čase O((n + m) log n). To lze teoreticky ještě zrychlit použitím Fibonacciho haldy, v praxi to ale není kvůli konstantě témeř žádný rozdíl a pro vyřešení úlohy to nebylo potřeba.
 34-1-2 Líný student (Zadání)
34-1-2 Líný student (Zadání)
Pojďme se zaměřit na první přednášku, kterou bude mít Vašek ve svém rozvrhu. Aby si nemohl přidat žádnou přednášku ještě před ni, tak jeho první přednáška musí začínat dříve, než nějaká jiná končí. Možností pro výběr první přednášky je ovšem více, kterou si má vybrat?
Když si nějakou vybere, tak si ze seznamu přednášek může odmyslet všechny, které s ní mají nějaký překryv. Už totiž nemůže žádnou z nich přidat do rozvrhu a tedy mu ani žádná z nich nemůže být vnucena. V uvažovaných přednáškách tak zůstanou jenom přednášky začínající po konci té vybrané. Všimněme si, že zbývající přednášky zase tvoří zadání naší úlohy. Chceme z nich totiž vybrat co nejméně nepřekrývajících se přednášek tak, aby žádnou další do výběru již nešlo přidat.
Všimneme si, že když si setřídíme přednášky podle času jejich začátku, tak si při každém výběru první přednášky odmyslíme nějaký začátek tohoto seznamu. Zbudou nám jenom přednášky, které začínají po konci vybrané přednášky.
Uvažujme i nadále setříděný seznam přednášek podle času jejich začátku. Částem seznamu od nějaké přednášky dále budeme říkat sufixy přednášek. V případě, že už budeme mít vyřešenou naši úlohu pro všechny sufixy přednášek (kromě toho obsahující všechny přednášky), tak již není problém vyřešit i celý seznam přednášek. Podíváme se na všechny možnosti, jakou přednášku vybrat jako první. Pro každou z nich zjistíme, kolik dalších přednášek bychom museli vybrat, a vybereme si optimální možnost.
Při rozhodování, kterou přednášku vybrat, tedy potřebujume mít zpracované všechny sufixy od této přednášky dále. Můžeme tedy začít tak, že si nejprve vyřešíme úlohu pouze pro poslední přednášku, a pak postupně řešíme delší a delší sufixy přednášek. Tomuto postupu se říká dynamické programování.
Popsaným algoritmem zjistíme, kolik předmětů si bude Vašek muset zapsat, ovšem zatím nevíme, které to jsou. Pro každý sufix přednášek si ještě kromě minimálního počtu zapamatujeme, na kterou přednášku má Vašek v daném sufixu jít jako první. Pomocí toho pak zvládneme postavit celé řešení. Vždy se podíváme, na kterou přednášku má zajít, a dále se podíváme na sufix přednášek po jejím konci. Toto opakujeme, dokud nezmizí všechny přednášky.
Popsané řešení je ovšem vcelku pomalé. Pro každou část seznamu totiž prochází všechny přednášky, kterými může začít, a pro každou z nich hledáme odpovídající zbylý sufix. Celková časová složitost je tedy O(N3). Pojďme ho zrychlit!
K přednáškám si poznačíme, jaký sufix přednášek po jejich vybrání zbude, abychom jej nemuseli pokaždé hledat. To můžeme pro každou přednášku zjistit pomocí jednoho binárního vyhledávání – najdeme první přednášku začínající po jejím konci.
V průběhu počítání sufixů si můžeme pamatovat, kdy nejdříve končí některá z přednášek v sufixu. Při rozšíření sufixu tuto hodnotu zvládneme jednoduše přepočítat.
Nyní zbývá pouze výběr optimální přednášky. Víme, že přednášky, které můžeme pro daný sufix vybrat jako první, tvoří v setříděném seznamu nějaký souvislý interval – musí ležet v uvažovaném sufixu a musí začínat před prvním koncem přednášky ze sufixu. Nabízí se tedy použít intervalový strom na hledání minima postavený nad posloupností přednášek. Hodnota přednášky bude říkat, jakého počtu přednášek umíme dosáhnout jejím vybráním.
Ovšem musíme si rozmyslet, jak onen intervalový strom vzniká. Na začátku totiž ještě neznáme hodnoty v něm, ty zjišťujeme až průběžně. Naštěstí hodnoty do intervalového stromu přidáme před tím, než je budeme potřebovat. Chceme-li přidat přednášku, podíváme se na sufix začínající po jejím konci. Ten už máme zpracovaný, položíme tedy intervalový dotaz a tím zjistíme hodnotu přidávané přednášky.
Celková časová složitost bude díky použití binárního vyhledávání a intervalového stromu O(N log N). Paměťová složitost bude O(N).
 34-1-3 Pilný student (Zadání)
34-1-3 Pilný student (Zadání)
Na začátek si ujasněme, že Filip je doopravdy pilný student, a protože se snaží maximalizovat počet bodů za splněné úkoly, udělá úkol vždy, když může – tedy nemá mezi plněním úkolů zbytečné mezery.
Teď se pojďme zamyslet nad tím, co nám o možnosti splnění úkolu prozradí jeho deadline. K tomu se nám bude hodit informace o celkovém počtu úkolů. Kdykoliv máme úkol, jehož deadline je větší než celkový počet úkolů N, víme, že tento úkol určitě stihne vypracovat. I kdyby totiž splnil všechny úkoly kromě tohoto úkolu, zabere mu jejich plnění maximálně N - 1 dní. Na tento úkol mu tedy vždy alespoň jeden volný den zůstane.
Dále si pojďme rozmyslet, jaké úkoly může Filip v jeden konkrétní den D splnit. Vždy se jedná o úkoly s deadlinem, který je větší nebo roven D. Na počátku si můžeme k vypracování vybrat libovolný úkol, ale postupem času se počet nesplněných úkolů zmenšuje (protože postupně propadají). Uvědomme si, že je nám u každého úkolu v podstatě jedno, kdy ho Filip splní, pouze nás zajímá, zda ho splní. Tudíž úkoly s delším deadlinem chceme plnit co nejpozději, abychom měli případně čas dělat úkoly s kratším deadlinem. Z toho vyplývá, že chceme při rozvrhování postupovat od konce.
Jako poslední chceme plnit úkoly s deadlinem větším než N. Všimněme si, že nám nevadí plnit ostatní úkoly dříve, neboť dní na to máme dost (jak jsme zmínili ve druhém odstavci). Následně budeme rozvrhovat odzadu – vždy se podíváme na úkoly s deadlinem daný den a nerozvržené úkoly s pozdějším deadlinem, protože to jsou ty, které může Filip ještě splnit. Z nich vybereme úkol s nejvyšším bodovým ziskem a rozvrhneme ho. Pro výběr úkolu s nejvyšším bodovým ziskem můžeme použít maximovou haldu. Následně se podíváme na předchozí den a opakujeme postup (do haldy přidáme nové úkoly a vybereme z ní maximum).
V průběhu algoritmu do haldy každý úkol nejvýše jednou přidáme a nejvýše jednou ho z ní odebereme. Přidání/odebrání prvku z/do haldy umíme realizovat v čase O(log N). Celková časová složitost je tedy O(N log N). Paměťová složitost je lineární vzhledem k N.
 34-1-4 Sjezdař (Zadání)
34-1-4 Sjezdař (Zadání)
Tyčkové lemma
Nejprve si ukážeme, že má smysl lámat lomenou čáru sjezdaře pouze v krajních bodech branek (těm budeme říkat tyčky). Z každého přípustného řešení úlohy (a tedy i toho optimálního) vyrobíme řešení, kde se bude lomená čára lámat pouze v tyčkách a jeho strmost nebude menší.
Budeme postupně odebírat zlomy mimo tyčky, až dospějeme do stavu, kdy žádný zlom mimo tyčku nebude existovat.
Podívejme se na libovolný zlom B mimo tyčku a úsečky lomené čáry před (AB) a za (BC) ní. V případě, že body AC lze propojit úsečkou bez minutí žádné branky, touto úsečku můžeme nahradit dané dva segmenty lomené čáry. Strmost se tím nezhorší. V opačném případě posuneme bod B vodorovně ve směru, kam lyžař zatáčel, dokud bude lomená čára protínat všechny branky. Tím trasu sjezdaře vlastně narovnáváme a tedy strmost se taky nezhoršuje.
Po tomto přesunu bude buď segment AB nebo BC procházet tyčkou. V bodě této tyčky přidáme zlom lomené čáry. Tím se trasa nijak nezmění. I když přibude jeden zlom v tyčce, bohužel nemusí ubýt žádný zlom mimo tyčku. Pokud ovšem zopakujeme algoritmus narovnávání nebo posouvání pro bod B, tak počet branek, ležících ve výšce po okolní body lomené čáry bude alespoň o jednu menší.
Branku, z jejíž tyčky jsme vytvořili nového souseda B, již totiž nebudeme muset řešit. Opakováním posouvání se bude počet branek snižovat. Tedy dřív nebo později musí nastat nahrazení za úsečku, protože počet branek se nemůže snižovat do nekonečna (pod nulu). U nahrazení za úsečku se už ovšem musí snížit počet zlomů mimo tyčky.
Opakováním předešlého algoritmu se tedy můžeme zbavit všech zlomů mimo tyčky bez zhoršení strmosti. Lemma tedy platí.
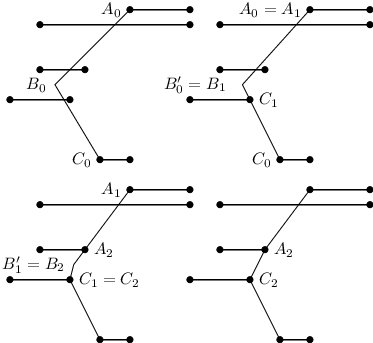
Poznámka: Alternativně můžeme říct, že příslušnou část lomené čáry mezi A a C nahradíme konvexním obalem tyček na straně, kam lyžař zatáčí.
Z důkazu také plyne, že v tyčkách má smysl lámat lomenou čáru jen směrem z branky ven. Řešení, kde by se zatáčelo do branky, totiž také zvládneme obdobně upravovat.
Lemma nám vlastně říká, že v následujících algoritmech má smysl uvažovat jen v jistém smyslu hezké trasy, protože mezi nimi bude alespoň jedna optimální.
Zadaná strmost
Pojďme se zamyslet nad tím, jak bychom plánovali trasu, pokud bychom měli pevně danou maximální strmost.
Budeme procházet branky v pořadí, v jakém jsou na svahu. U každé z nich si budeme počítat, kam všude do ní může vést nějaká trasa lyžaře. Algoritmem ukážeme, že možné pozice budou vždy tvořit úsečku.
U první branky může lyžař začít kdekoliv uvnitř ní. Pro každou další branku je jednak limitovaný tím, že danou brankou musí projet, a druhak musí umět na daný bod dojet z předchozí branky. Podíváme se na úsečku, kudy mohl projet předchozí brankou, a spočítáme si, kam by mohl dojet z ní na přímku aktuální branky. Jelikož je strmost omezená, víme, o kolik se může maximálně posunout do strany na jeden metr posunu ze svahu, a tedy není problém spočítat výslednou úsečku přípustných poloh.
Můžeme si to představit tak, že po průjezdu brankou spočítáme dosažitelnou oblast ve tvaru rovnoramenného lichoběžníku. Dále je nutné projet brankou. Tedy vezmeme průnik spočítané úsečky a úsečky branky. V případě, že průnik je prázdný, tak pro danou maximální strmost neexistuje řešení. V opačném případě bude průnikem úsečka (případně degenerovaná do jediného bodu).
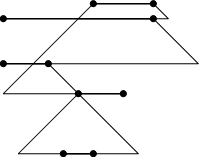
Pomocí předchozího algoritmu pak zvládneme trasu snadno zrekonstruovat. Začneme od poslední branky a vždy budeme volit průjezdy brankami tak, aby byly ve spočítané oblasti. Máme zaručeno, že i předchozí brankou bude možné projet ve spočítané oblasti.
Časová složitost algoritmu se odvíjí od toho, jak rychle zvládneme setřídit branky podle osy Y. Dále už je algoritmus lineární.
Předchozí algoritmus pro zadanou strmost umí najít řešení s alespoň tak dobrou strmostí, anebo rozhodnout, že žádné takové neexistuje. Tedy můžeme využít binárního vyhledávání na optimální strmosti. Problém ovšem je, že optimální strmost nemusí být celé číslo, a tedy se optimu umíme jen libovolně přiblížit, ale neumíme vyjádřit jeho přesnou hodnotu.
Kvadratické řešení
Nyní si ukážeme naprosto odlišné řešení. Podíváme se na každou dvojici branek a spočítáme si, s jakou největší strmostí lze přejet z první do druhé, kdyby to byly jediné dvě branky na trati. Když se branky v x-ové souřadnici překrývají, tak je to +∞. V opačném případě se jen podíváme na strmost mezi bližší dvojicí tyček.
Minimum přes všechny dvojice branek je evidentně větší nebo rovné optimu celé úlohy. To proto, že přidáváním branek k dané dvojici se řešení nemůže zlepšit.
Z tyčkového lemmatu víme, že alespoň jedno optimální řešení láme lomenou čáru jen v tyčkách branek. Tedy úsek s nejmenší strmostí musí odpovídat strmosti mezi dvojicí tyček. Jelikož u tyček se vždy zatáčí ven z branky, tak jedna z tyček musí byt levá a druhá pravá. Jinak bychom na jedné straně zahnuli tak, že by se strmost snížila.
Speciálním případem jsou krajní části lomené čáry. U nich ale nahlédneme, že je bez zhoršení strmosti můžeme buď narovnat na svislé, a nebo tak, že na jejich okraji také bude tyčka, u které se bude zatáčet tak, jako kdyby před resp. za ní byl svislý úsek.
Úsek s největší strmostí optimálního řešení je vlastně strmost mezi dvojicí branek. My jsme ovšem vyzkoušeli všechny dvojice branek, a tedy minimum z jejich strmostí musí být menší než strmost optimálního řešení.
Složením předchozích pozorování tedy víme, že spočítané minimum je strmost optimálního řešení. Pomocí předešlého algoritmu pak již zvládneme se znalostí optimální strmosti spočítat trasu.
Časová složitost tohoto řešení je O(N2), protože procházíme všechny dvojice branek.
Rychlé řešení
A nyní už si ukážeme poslední řešení. Znovu budeme procházet branky v pořadí ze svahu dolů. Ovšem tentokrát místo počítání dosažitelné oblasti budeme uvažovat oblasti, u kterých si budeme pamatovat poslední tyčku při cestě do ní a strmost nutnou k dosažení dané tyčky. Na začátku budeme mít ještě speciální oblast dosažitelnou se strmostí +∞. Hranicemi mezi oblastmi budou přímky.
Po projetí první branky budeme mít tři oblasti. Svisle pod brankou bude oblast se strmostí +∞. Zbytek pak budou oblasti příslušející daným tyčkám. K dosažení tyček na začátku také stačí strmost +∞.
Při průchodu každé další branky nejprve zahodíme oblasti, které se dále nemůžou projevovat. Tedy ty, které minou branku. Pokud nějaká oblast leží zčásti uvnitř a zčásti mimo branku, omezíme její okraj přímkou spojující tyčku dané oblasti a tyčku aktuální branky. Na oba okraje pak přiděláme oblast odpovídající tyčkám aktuální branky.
Ještě musíme spočítat optimální strmost k dosažení tyček branky. Tu určíme z oblastí, ve kterých tyčky ležely. Vezmeme minimum ze strmosti oblasti a strmosti spojnice tyčky oblasti a aktuální tyčky. To si můžeme představit tak, že prodloužíme jedním úsekem trasu k tyčce oblasti. V případě, že tyčka leží na hraně více oblastí, je jedno, kterou vezmeme.
Až projdeme všechny branky, podíváme se na všechny aktuální oblasti. U každé spočítáme minimální strmost na dosažení jejího průniku s poslední brankou. Z těchto hodnot vezmeme minimum.
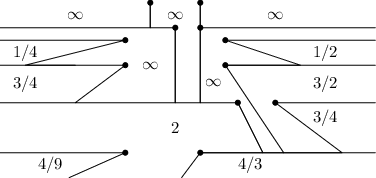
Oblasti si můžeme udržovat v oboustranně propojeném spojovém seznamu. Odebírat budeme vždy z krajů. U každé branky trávíme až na odebírání nedostupných oblastí konstantní čas. Ovšem každou oblast, kterou jsme odebrali, jsme museli jednou přidat. Proto se celková složitost uamortizuje na O(N) až na třídění branek dle y-ové souřadnice.
Celý algoritmus tedy běží v čase O(N log N) a prostoru O(N).
 34-1-X1 Rostoucí strom (teoretická) (Zadání)
34-1-X1 Rostoucí strom (teoretická) (Zadání)
Pojďme se nejprve zamyslet nad statickou verzí úlohy. V ní nejdříve přijdou všechny požadavky na přidání vrcholu, a až po nich začnou přicházet dotazy na vzdálenost a požadavky na prodloužení. Tedy se na začátku postaví strom a až pak se s ním pracuje. Po dostavění stromu si můžeme vybudovat nějakou datovou strukturu a pak ji jenom updatovat a ptát se na vzdálenosti vrcholů od kořene. K tomu lze využít například heavy-light dekompozice ze seriálu o stromech.
My si zde ovšem ukážeme jiné řešení, které pak zobecníme i na strom, kde přibývají vrcholy. Na postaveném stromu si pustíme průchod do hloubky. Budeme tvořit posloupnost vrcholů. Když do vrcholu přijdeme nebo z něj odejdeme zpět ke kořeni, přidáme ho do posloupnosti. Na začátek a konec posloupnosti ještě přidáme kořen. Každý vrchol tedy bude v posloupnosti právě dvakrát. U každého vrcholu si budeme pamatovat dva indexy, kde v posloupnosti se vyskytuje.
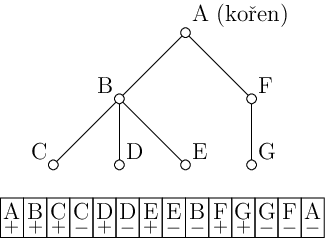
K prvnímu výskytu vrcholu v posloupnosti připíšeme délku hrany, která do něj vede. K druhému výskytu pak připíšeme opačnou hodnotu. (Pro kořen můžeme uvést dvě nuly.) Pro zjištění vzdálenosti vrcholu od kořene pak stačí sečíst prefix posloupnosti po první výskyt požadovaného vrcholu. Všimneme si, že každá hrana na cestě mezi kořenem a vrcholem je do součtu přičtena. Ovšem každá jiná hrana je buď již přičtená a odečtená, anebo v prefixu vůbec není.
Můžeme si tedy postavit intervalový strom. Pro prodloužení hrany provedeme dva updaty intervaláče a pro dotazy na vzdálenost odpovíme součtem intervalu (prefixu).
Statickou verzi tedy zvládneme řešit v čase O(N log N), kde N je délka vstupu.
Pojďme nyní přejít na dynamickou verzi. Navíc tedy dovolíme mezi dotazy a prodlouženími hran zadávat požadavky na přidání nové hrany a vrcholu.
To v našem případě znamená přidat do posloupnosti dva nové odkazy na vrchol. Nahlédneme, že stačí přidat oba dva záznamy o novém vrcholu těsně za první výskyt jeho předka.
Ovšem do intervalového stromu nelze přidávat další prvky efektivně. Proto intervalový strom budeme muset nahradit za něco chytřejšího. Posloupnost vrcholů tedy budeme reprezentovat pomocí vyvažovaného stromu. Například pomocí treapu nebo třeba splay stromu. Do takto reprezentované posloupnosti umíme přidávat další prvky, updatovat jejich hodnoty a dokonce sčítat hodnoty na intervalu. To vše v čase lineárním k hloubce stromu. Pro vhodnou implementaci stromů tedy v logaritmickém čase k velikosti stromu.
Celková časová složitost je tedy O(N log N), kde N je délka vstupu.
 34-1-X2 Rostoucí strom (praktická) (Zadání)
34-1-X2 Rostoucí strom (praktická) (Zadání)
 34-1-S Manimujeme – úvod (Zadání)
34-1-S Manimujeme – úvod (Zadání)
K letošnímu seriálu nevydáváme řešení v klasické podobně, nicméně můžete se podívat na programy a animace od řešitelů: http://ksp.mff.cuni.cz/viz/34-5-S/komentare