První série třicátého čtvrtého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám první číslo hlavní kategorie 34. ročníku KSP.

Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Také na kuchařky na nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly budou vycházet samostatně.

Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.

Odměny & na Matfyz bez přijímaček

• Termín série: 31. října 2021 ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Každému, kdo vyřeší 4 úlohy alespoň na polovinu bodů, pošleme sladkou odměnu.

Zadání úloh

• 34-1-1: Běžkař
• 34-1-2: Líný student
• 34-1-3: Pilný student
• 34-1-4: Sjezdař
• 34-1-S: Manimujeme – úvod
• 34-1-X1: Rostoucí strom (teoretická)
• 34-1-X2: Rostoucí strom (praktická)

34-1-1 Běžkař (10 bodů)

Kevin si na jaře vyrazil na Šumavu na běžky. Jenže na některých místech už je sníh téměř roztátý, takže se na běžkách místy pohybuje velice obtížně. Časté sundavání a nandavání běžek je ale časově náročné a Kevin by se potřeboval na hotel dostat co nejrychleji.

Mapu Šumavy si můžeme představit jako neorientovaný graf (pokud nevíte, jak takový graf vypadá, doporučujeme si přečíst kuchařku). Mezi křižovatkami vedou cesty, které mají ohodnocení: kolik minut Kevinovi zabere projet cestu na běžkách a za jak dlouho ji projde se sundanými běžkami. Sundávat a nasazovat běžky Kevin může pouze na křižovatce a zabere mu to K minut. Na začátku má Kevin běžky nasazené, na konci cesty je musí mít sundané.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete počet křižovatek N, počet cest M, na kolikáté křižovatce se Kevin nachází, na kolikátou křižovatku se chce dostat a čas sundavání a nandavání běžek K. Na každém z následujících M řádků budou 4 čísla: A_i, B_i, X_i a Y_i.

Hodnoty A_i a B_i určují, mezi kterými dvěma křižovatkami vede i-tá cesta. X_i určuje, jak dlouho Kevinovi potrvá cestu přejet na běžkách, a Y_i určuje, jak dlouho ji potrvá přejít pěšky.

Všechny vrcholy jsou očíslovány od 0 do N - 1 včetně.

Formát výstupu: Na výstup vypište jediné číslo – nejkratší čas, za který je Kevin schopen se dostat do cíle.

3 3 0 2 3
0 1 2 3
1 2 5 4
2 0 50 50

9

Řešení

34-1-2 Líný student (11 bodů)

Se začátkem semestru si začal Vašek zapisovat přednášky. Jenže se bojí, aby si předmětů nezapsal příliš, a měl vůbec čas i na přípravu KSP. Ovšem rád by zabránil tomu, aby za ním mohl přijít nějaký jeho kamarád a říct mu, ať si zapíše ještě nějakou další přednášku.

Každá přednáška je popsána časem začátku a konce. Všechny časy začátků a konců přednášek jsou navzájem různé.

Vašek si tedy chce vybrat přednášky tak, aby jich byl co nejmenší počet. Ovšem ještě chce, aby nemohl v době volného času stihnout navštěvovat ještě nějakou jinou přednášku od začátku do konce. Vymyslete algoritmus, který tyto přednášky za Vaška vybere.

Řešení

34-1-3 Pilný student (12 bodů)

Filip nastoupil na vysokou školu a nestačil se divit. Tolik úkolů, to na střední nebývalo! A jak jsou dlouhé!

Každý z N úkolů má určitý počet bodů B za své splnění, a navíc má deadline, tedy datum, do kterého Filip úkol musí vypracovat. Deadline každého úkolu je specifikován jediným číslem D, totiž počtem dní (od teď), do kdy úkol musí být splněn (tedy například pokud D = 1, tak musí Filip splnit úkol buď dneska, nebo zítra). Pokud do tohoto data Filip úkol neudělá, tak úkol propadá a už za něj nemůže získat žádné body.

Filip ví, že za jeden den stihne splnit nejvýše jeden úkol. Nyní si chce rozvrhnout čas tak, aby maximalizoval počet získaných bodů. Pomozte mu s tím.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete číslo N: počet úkolů, které Filip má zadané. Na každém z následujících N řádků bude popsán jeden úkol dvěma mezerou oddělenými čísly B a D, tedy počtem bodů za daný úkol a deadline daného úkolu.

Formát výstupu: Na první řádek vypište jediné číslo: maximální počet bodů, které Filip může získat, pokud si rozvrhne čas dobře. Na následujících N řádcích pak vypište jedno z možných optimálních řešení. Pro každý úkol vypište jeden řádek obsahující den, ve který Filip má daný úkol řešit, nebo případně -1, když ho řešit nemá.

5
9 1
3 0
8 2
7 1
2 2

24
0
-1
2
1
-1

Řešení

34-1-4 Sjezdař (12 bodů)

Na svahu tvořeném nakloněnou rovinou je umístěno N závodních branek. Po tomto svahu jede sjezdař z kopce dolů po trase určené lomenou čárou, která musí projít všemi brankami. Branka je horizontální úsečka zadaná třemi čísly: jedna souřadnice Y a dvě souřadnice X určující pozici krajních bodů. Trasa sjezdaře musí protnout tuto úsečku (může také procházet jedním z krajních bodů). Pokud jsou souřadnice obou krajních bodů stejné, musí sjezdař projet přesně tímto bodem. Osa X směřuje horizontálně, osa Y směřuje dolů ze svahu.

Vaším úkolem je vymyslet algoritmus, který najde trasu s největší možnou strmostí. Strmost trasy nadefinujeme jako minimum ze strmostí jednotlivých úseků. Strmost úseku lomené čáry z bodu (x₁, y₁) do bodu (x₂, y₂) pak je (y₂ - y₁)/|x₂ - x₁|. Pokud x₁ = x₂ a y₂ > y₁, strmost vyjde nekonečná. (Případ, že y₂ < y₁, nemůže nastat – znamenalo by to, že sjezdař jede do kopce.)

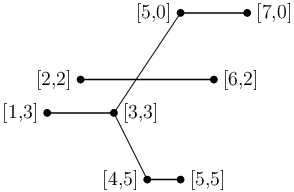
Uvažujme následující příklad rozložení branek (každá branka je popsaná pomocí tří čísel – dvou x-ových souřadnic a jedné y-ové):

5 7 0
2 6 2
1 3 3
4 5 5

Řešení

34-1-X1 Rostoucí strom (teoretická) (8 bodů)

Kristýna se nedávno rozhodla k uctění hroších bohů založit arboretum. Zde hodlá pěstovat vzácný druh stromů – hrošeň.

Zatím má pouze jediné semínko představující první vrchol stromu – kořen. Strom bude postupně růst a Kristýnu vždy bude zajímat vzdálenost nějakého vrcholu od kořene (aby měla přehled, které vrcholy jsou dostatečně vysoko, takže hroší bohové na ně určitě uvidí). Hrany stromu budou mít různé délky a vzdáleností myslíme součet délek na cestě mezi daným vrcholem a kořenem.

Úkolem je zpracovávat následující operace:

• K určitému vrcholu přivěs nový hranou délky jedna.
• Hranu vedoucí do daného vrcholu prodluž o určitou délku.
• Vypiš vzdálenost určeného vrcholu od kořene.

Na operace je potřeba odpovídat online. To znamená, že po načtení dotazu třetího typu je třeba vypsat výsledek předtím, než načtete další řádek vstupu.

Řešení

34-1-X2 Rostoucí strom (praktická) (8 bodů)

Jelikož je uctívání hroších bohů ryze praktická záležitost, nyní si předchozí úlohu naimplementujeme!

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Vrcholy číslujeme postupně od nuly. Kořen má tedy číslo nula. První typ operace přidá vždy vrchol s nejmenším zatím nepoužitým číslem.

Vstupem je binární soubor. Skládá se z čísel, každé je uložené v pořadí od nejméně významného bytu k nejvýznamnějšímu (tzv. little-endian formát).

Vstup začíná čtyřbytovým číslem Q, které značí počet operací. Následuje Q bloků po čtyřech bytech, každý reprezentuje jednu operaci. Každý z nich se skládá z jednoho trojbytového čísla A a jednoho jednobytového čísla B. Nechť O je odpověď na předchozí dotaz na vzdálenost (pokud ještě žádná nebyla, tak 0) a N je aktuální počet vrcholů. Označme X = (A + O) mod 3N. Podle hodnoty X daný blok reprezentuje určitou operaci:

• Když 0 ≤ X < N, k vrcholu X přivěs nový vrchol hranou délky 1.
• Když N ≤ X < 2N, hranu vedoucí do vrcholu X - N prodluž o B. (Je zaručeno, že se nejedná o kořen.)
• Když 2N ≤ X < 3N, zjisti vzdálenost vrcholu X - 2N od kořene.

Výstupem je textový soubor obsahující jediné číslo – odpověď na poslední otázku na vzdálenost.

Šablona řešení (C++)

Řešení

34-1-S Manimujeme – úvod (15 bodů)

Letošním ročníkem vás bude provázet seriál. V každé sérii se objeví jeden díl, který bude obsahovat nějaké povídání a navíc úkoly. Za úkoly budete moci získávat body podobně jako za klasické úlohy série. Abyste se mohli zapojit i během ročníku, seriál bude možné odevzdávat i po termínu za snížený počet bodů. Vzorové řešení seriálu proto před koncem celého ročníku KSP uvidí jen ti, kdo už seriál odevzdali.

Animace jsou lepší než obrázky, ať už se jedná o prezentování zajímavého nápadu či vizualizaci běhu algoritmu. Proto je šikovné umět pěkné animace vytvářet, nejlépe programaticky. Právě k tomu slouží Pythoní knihovna Manim, vytvořená Grantem Sandersonem (3b1b na YouTube), o které tento ročník seriálu bude.

Co bude potřeba

Ke čtení seriálu se bude hodit základní znalost Pythonu, ve kterém budeme animace programovat. Užitečná bude také základní znalost sázení matematiky v TeXu, ale k té existuje řada vizuálních editorů, takže neznalost příliš nevadí. Instalace programů jiných než Pythonu potřeba nebude, jelikož budeme Manim spouštět interaktivně v prohlížeči.

Jupyntermezzo

Každým dílem seriálu nás bude provázet Jupyter (v kombinaci s Binderem), ve kterém budeme s Manimem pracovat. Jedná se o webovou aplikaci, která umožňuje vytvářet textem doprovázený kód a spouštět jej přímo v prohlížeči. Dokument, ve kterém jdou všechny zdrojové kódy k tomuto dílu seriálu spustit (a upravovat), se nachází na tomto odkazu.

Pokud chcete Manim instalovat na svůj počítač, abyste jej mohli používat i bez přístupu k internetu, tak můžete využít tento návod, který podrobně popisuje instalaci na každém z populárních operačních systémů. Po instalaci budete mít k dispozici příkaz manim, který lze použít (v základním tvaru) následně: manim <jméno souboru> -pqm <jméno scény>. -p zde Manimu říká, že chcete výsledek rovnou vidět a qm nastavuje kvalitu na medium (lze použít také low, high a 4k).

Úvod

Základní stavební blok Manimu jsou scény. Jedná se o Python třídy, které dědí Manimovou třídu Scene. Každá třída scény musí obsahovat metodu construct, která obsahuje informace o tom, jaké útvary se po zavolání Manimu mají vykreslit a co se s nimi má dít (posouvání, změna barev/velikosti, apod.).

Zde je příklad jednoduché scény, která nejprve vykreslí a následně schová červený čtverec a modrý kruh.

from manim import *

class Intro(Scene):
    def construct(self):
        # vytvoření objektů čtverce a kruhu (a jejich posunutí)
        square = Square(color=RED).shift(LEFT * 2)
        circle = Circle(color=BLUE).shift(RIGHT * 2)

        # napsaní čtverce a kruhu na scénu
        self.play(Write(square), Write(circle))

        # schování čtverce a kruhu ze scény
        self.play(FadeOut(square), FadeOut(circle), run_time=2)

Metoda self.play vždy očekává libovolný nenulový počet animací, které má najednou provést. Výše ji voláme s animacemi Write, které objekty najednou vykreslí, a FadeOut, které je schová. Její volitelný parametr run_time určuje, jak dlouho má animace trvat (ve vteřinách). Pokud není specifikovaný, tak bude animace trvat 1 vteřinu.

V kódu se rovněž objevuje řada konstant (LEFT, RIGHT, RED, BLUE). Jedná se o vestavěné konstanty, které Manim používá ke zpřehlednění čitelnosti kódu. Obsahuje jich spoustu – kromě těchto jsou dále užitečné například UP, DOWN a <anglické jméno barvy> (ORANGE, GREEN, apod.), které budeme často používat.

Po vytvoření obou objektů na nich voláme metodu shift, která je posune daným směrem a zároveň vrátí. Tak funguje naprostá většina metod, které objekt nějakým způsobem upravují, abychom nemuseli (ale pokud bychom opravdu chtěli tak můžeme) psát následující:

square = Square(color=RED)
square.shift(LEFT * 2)

Jelikož jsou směrové proměnné interně pouze vektory, tak je jde jak sčítat, tak násobit konstantami. Pro pohyb šikmo je tedy nejjednodušší použít např. obj.shift(LEFT + UP * 1.5) (místo obj.shift(LEFT).shift(UP * 1.5)).

animate syntax

Kromě vytváření a mizení objektů by se nám hodilo animovat jejich různé vlastnosti, jako barvu, pozici či otočení. Výše uvedená funkce shift sice pozici upravuje, ale posun nevykreslí.

V Manimu jde animace vlastností docílit několika různými způsoby, ze kterých je bezesporu nejelegantnější tzv. animate syntax: vložením magického slova animate za animovaný objekt můžeme vlastnosti upravit v animaci:

from manim import *

class Animate(Scene):
    def construct(self):
        square = Square(color=RED).shift(LEFT * 2)
        circle = Circle(color=BLUE).shift(RIGHT * 2)

        self.play(Write(square), Write(circle))

        # posunutí objektů
        self.play(square.animate.shift(UP * 0.5), circle.animate.shift(DOWN * 0.5))

        # otočení a vybarvení vnitřku čtverce (průhlednost 80%)
        # zvětšení a vybarvení vnitřku kruhu (průhlednost 80%)
        self.play(
            square.animate.rotate(PI / 2).set_fill(RED, 0.8),
            circle.animate.scale(2).set_fill(BLUE, 0.8),
        )

        # úplné přebarvení kruhu i čtverce (obrys i výplň)
        # stejné jako .set_fill() + .set_stroke()
        self.play(
            square.animate.set_color(GREEN),
            circle.animate.set_color(ORANGE),
        )

        self.play(FadeOut(square), FadeOut(circle))

Ukázka obsahuje některé z vlastností, které má každý objekt (pozici, otočení, barvu...) a mohou být plynule animovány. Jak je z kódu vidět, animace jde řetězit a měnit tak více vlastností najednou, jen je třeba si dávat pozor na to, aby se stejná vlastnost neměnila na dvě různé hodnoty.

Animování kolekce objektů

Prakticky vždy, když vytváříme animace programaticky, se nám hodí umět najednou animovat celou řádu objektů, uloženou například v poli či n-tici. Prozatím se naučíme způsob, který s Manimem nemá nic společného, ale jedná se pouze o pokročilou vlastnost Pythonu.

V Pythonu funguje rozbalování pole/n-tice do parametrů funkce pomocí operátoru *:

def add_numbers(a, b):
    return a + b

numbers = [1, 2]

result = add_numbers(*numbers)
# stejné jako add_numbers(numbers[0], numbers[1])

print(result)  # vypíše 3

Stejného triku můžeme využít při animování pole objektů:

square = [Square().shift(LEFT), Square(), Square().shift(RIGHT)]

self.play(*[Write(s) for s in square])

V některém z dalších dílů se dozvíme o VGroup objektech, které mohou být k animaci kolekce objektů v některých případech vhodnější, prozatím nám ale tento způsob bude stačit.

Posouvání objektů

V předchozích ukázkách jsme se seznámili s funkcí shift, která objekt posune do nějakého směru. Někdy bychom ale chtěli posunout objekty v závislosti na ostatních objektech – aby byly vedle sebe, nad sebou, v sobě, apod.

Pro posunutí objektu vedle druhého použijeme funkci next_to:

from manim import *

class NextTo(Scene):
    def construct(self):
        # vytvoření čtyřech menších kruhů
        c1, c2, c3, c4 = [Circle(radius=0.5, color=WHITE) for _ in range(4)]

        # a jednoho obélníku
        rectangle = Rectangle(width=5, height=3)

        self.play(*[Write(o) for o in [c1, c2, c3, c4, rectangle]])

        # posunutí kruhů tak, aby byly okolo obdélníku
        self.play(
            c1.animate.next_to(rectangle, LEFT),  # nalevo od
            c2.animate.next_to(rectangle, UP),  # nahoře od
            c3.animate.next_to(rectangle, RIGHT),  # napravo od
            c4.animate.next_to(rectangle, DOWN),  # dolů od
        )

Pro posunutí objektu na druhý použijeme funkci move_to:

from manim import *

class MoveTo(Scene):
    def construct(self):
        s1, s2, s3 = [Square() for _ in range(3)]

        self.play(*[Write(o) for o in [s1, s2, s3]])

        # posunutí čtverců vedle sebe
        self.play(
            s1.animate.next_to(s2, LEFT),
            s3.animate.next_to(s2, RIGHT),
        )

        # jim odpovídající čísla
        t1, t2, t3 = [Tex(f"${i}$").scale(3) for i in range(3)]

        # posunutí čísel do středů čtverců
        t1.move_to(s1)
        t2.move_to(s2)
        t3.move_to(s3)

        self.play(*[Write(o) for o in [t1, t2, t3]])

Pro posunutí objektu "na stejnou úroveň" jako druhý použijeme funkci align_to:

from manim import *

class AlignTo(Scene):
    def construct(self):
        # vytvoření tří různě velikých kruhů
        c1, c2, c3 = [Circle(radius=1.5 - i / 3, color=WHITE) for i in range(3)]
        
        self.play(*[Write(o) for o in [c1, c2, c3]])
        
        # c1 a c3 vedle c2
        self.play(
            c1.animate.next_to(c2, LEFT),
            c3.animate.next_to(c2, RIGHT),
        )
        
        # spodek c1 a c3 je stejný jako c2
        self.play(
            c1.animate.align_to(c2, DOWN),
            c3.animate.align_to(c2, DOWN),
        )
        
        # vršek c1, c2 a c3 je vyrovnaný s bodem
        point = Point([0, 2.5, 0])
        
        self.play(
            c1.animate.align_to(point, UP),
            c2.animate.align_to(point, UP),
            c3.animate.align_to(point, UP),
        )

Jak je z kódu vidět, funkce umí kromě vyrovnávání podle objektu také vyrovnávat podle bodu.

Sázení textu a matematiky

Jelikož byl Manim vytvořený převážně ke tvorbě matematicky-zaměřených animací, tak podporuje sázení TeXu (včetně matematiky). K sázení textu budeme používat Tex objekt, k sázení matematiky MathTex.

Pokud TeXovou matematiku psát neumíte, tak můžete použít online editor (jako například tento), který vám psaní značně usnadní.

from manim import *

class TextAndMath(Scene):
    def construct(self):
        text = Tex("Tohle je text!").shift(LEFT * 2.5)

        # ke snazšímu psaní \ používáme r-stringy (před stringem je 'r')
        # znamená to, že znaky '\' jsou brány doslova (v normálním stringu by bylo potřeba psát \\)
        formula = MathTex(r"\sum_{i = 0}^\infty \frac{1}{2^i} = 2").shift(RIGHT * 2.5)

        self.play(Write(formula), Write(text))

        self.play(FadeOut(formula), FadeOut(text))

Úlohy

K odevzdávání úloh lze animaci vytvořit buď online přímo v Jupyteru pro tento díl (na konci dokumentu je kostra pro každou z úloh, do které ji jde přímo doprogramovat), nebo i lokálně, pokud máte nainstalovný Manim.

Odevzdávejte celý zdrojový kód v zazipovaném (a nezaheslovaném) archivu.

V každé z úloh této i nadcházejících dílů je cílem naprogramovat animaci obecně, ne jen pro jeden vstup. Animace by za vás měl dělat nějaký algoritmus, rozhodně byste ji neměli programovat manuálně (pohyb za pohybem).

Úkol 1 – Míchání [4b]

Naprogramujte animaci náhodného míchání kuliček:

K prohazování se vám bude hodit animace Swap, která prohodí pozici dvou objektů. Možná se vám také může hodit její volitelný parametr path_arc, který určuje, pod jakým úhlem prohození proběhne:

from manim import *

class Sort(Scene):
    def construct(self):
        c11 = Circle(color=WHITE).shift(UP * 1.5 + LEFT * 2)
        c12 = Circle(color=WHITE).shift(UP * 1.5 + RIGHT * 2)
        c21 = Circle(color=WHITE).shift(DOWN * 1.5 + LEFT * 2)
        c22 = Circle(color=WHITE).shift(DOWN * 1.5 + RIGHT * 2)

        self.play(Write(c11), Write(c12), Write(c21), Write(c22))

        self.play(Swap(c11, c21))

        self.play(Swap(c12, c22, path_arc=160 * DEGREES))

Úkol 2 – Třízení [6b]

Naprogramujte animaci nějakého třídícího algoritmu pro náhodně vygenerovaný vstup:

Pro tuto úlohu se vám bude hodit funkce objektu stretch_to_fit_height (v použití s animate syntaxem), která změní výšku objektu bez toho, aby zároveň proporcionálně měnila jeho šířku:

from manim import *

class StretchToFitHeightExample(Scene):
    def construct(self):
        s1 = Square().shift(LEFT * 2.5)
        s2 = Square().shift(RIGHT * 2.5)

        self.play(Write(s1), Write(s2))

        self.play(
            s1.animate.stretch_to_fit_height(3.5),
            s2.animate.set_height(3.5),
        )

Také bude užitečné používání funkce align_to s bodem (aby všechny obélníky byly ve stejné rovině).

Úkol 3 – Vyhledávání [5b]

Naprogramujte animaci binárního vyhledávání algoritmu pro náhodně vygenerovaný setřízený vstup:

Jako indikátory pozic se velmi hodí objekt Arrow. Vytvořit ho lze následně:

from manim import *

class ArrowExample(Scene):
    def construct(self):
        a1 = Arrow(start=UP, end=DOWN).shift(LEFT * 2)
        a2 = Arrow(start=DOWN, end=UP).shift(RIGHT * 2)

        self.play(Write(a1), Write(a2))

Tomáš Sláma

Řešení