Třetí série třicátého čtvrtého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám třetí číslo hlavní kategorie 34. ročníku KSP.

Opět se můžete těsit na dvě praktické a dvě teoretické úlohy. V této sérii se opět objeví pokračování Manimového seriálu, ale jeho zadání bude dostupné až po ukončení minulé série.

Odměny & na Matfyz bez přijímaček

• Termín série: 20. února 2022 ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Každému, kdo sepíše oslavnou báseň na hrochy o alespoň 8 verších, pošleme sladkou odměnu.

Zadání úloh

• 34-3-1: Ideální žádost
• 34-3-2: Faktoriál
• 34-3-3: Jízda tramvají
• 34-3-4: Horňáci a Dolňáci
• 34-3-S: Manimujeme – kamera a grafy
• 34-3-X1: Dráteníci

34-3-1 Ideální žádost (10 bodů)

Kevin již dlouhou dobu sedí v čekárně na úřadě, kde mezitím stihl dostat hrozný hlad. Rád by si skočil přes ulici ulovit něco k snědku, jenže vůbec netuší, kdy se v této podivné instituci dostane na řadu. S vidinou chutné bagety se proto snaží vypozorovat, v jakém pořadí jsou tady občané obsluhováni. Má podezření na nějaký podivný druh prioritní fronty.

V kanceláři pracují dva úředníci, před kterými je obrovská hromada žádostí od lidí z čekárny. Každou žádost trvá vyřídit nějaký známý čas (zadaný například počtem minut). Úředníci jsou ale líní a nechce se jim hned vyřizovat žádosti, které trvají příliš dlouho. Když si tedy úředník vybírá žádost, začne listovat hromádkou žádostí od vrchu a listuje tak dlouho, dokud nenajde první ideální žádost – tak označme žádost, po níž bezprostředně neleží jiná žádost, kterou by trvalo vyřídit kratší dobu.

Oba úředníci zpracovávají žádosti ze stejné hromady. Jakmile úředník nemá co dělat, najde si ideální žádost a vyřídí ji (úředníci jsou zkušení hledači ideálních žádostí a tak předpokládejme, že nalezení ideální žádosti trvá nulový čas). V jednom konkrétním čase vyřizuje úředník právě jednu žádost.

Pomozte Kevinovi určit, za jak dlouho stihnou úředníci vyřídit všechny žádosti, pokud se oba budou chovat podle výše popsaných pravidel.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Vstup: Na prvním řádku je číslo N – počet žádostí. Na druhém řádku je N celých kladných čísel reprezentující časové náročnosti jednotlivých žádostí. První číslo představuje vršek hromady, poslední číslo její spodek.

Výstup: Vypište jediné číslo – za kolik jednotek času budou všechny žádosti vyřízené.

7
8 6 5 2 3 4 1

16

Řešení

34-3-2 Faktoriál (11 bodů)

Filip dostal za úkol zjistit faktoriál velkého čísla, které mu zadal Petr. Číslo je ale opravdu velké, a tak usmlouval, že místo celého faktoriálu bude stačit spočítat počet nul na konci jeho zápisu. Aby to ale neměl Filip příliš jednoduché, tak musí být schopen výsledek určit pro libovolnou číselnou soustavu, kterou mu Petr zadá. Pomůžete mu s výpočtem?

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Vstup: Na vstupu dostanete jeden řádek s čísly N a K. N je číslo, jehož faktoriál Filip zkoumá, a K je základ číselné soustavy, v níž má počítat. Zajímá nás, kolik nul se nachází na konci zápisu N! v soustavě o základu K.

Například 7! je v desítkově soustavě 5040, což končí na jednu nulu, ve čtyřkové soustavě je to 1032300, což končí na dvě nuly.

Pozor! Číslo N může být opravdu velké. Slibujeme ale, že se vejde do 64-bitového intu, což si zajistíte například datovým typem long long v jazyce C nebo použitím Pythonu, který sám o sobě umí pracovat s velkými čísly.

Výstup: Na výstup vypište jedno číslo – počet nul na konci zápisu N! v soustavě o základu K.

42 10

9

Řešení

34-3-3 Jízda tramvají (12 bodů)

Jirka jede v tramvaji po Praze, a jelikož je tramvaj přeplněná, nemůže si sednout ani se něčeho chytit. Jenže, jak tramvaj během cesty zrychluje a různě zatáčí, na Jirku působí síly, které jej mohou vyhodit z rovnováhy a povalit na zem.

Když se Jirka trochu rozkročí, dokáže snadno udržet rovnováhu ve směru ze strany na stranu. Můžeme si představit, že takto ustojí libovolně velkou sílu, která na něj působí zleva nebo zprava. Ale pokud na něj zapůsobí síla zepředu nebo zezadu, pak ustojí pouze síly velké nejvýše F₀. Větší síla v tomto směru povede k nemilému pádu.

Naštěstí Jirka nejede cestou poprvé a dopředu ví, jaké síly na něj budou působit v jakou chvíli, a může se vždy natočit tak, aby nespadl. Samozřejmě by se mohl vždy natočit bokem vůči síle, ale to je příliš pracné. Stačí, když se natočí jen částečně. Pak se síla rozloží do čelního a bočního směru, přičemž velikost síly v čelním směru nesmí přesáhnout F₀.

Naším úkolem tak bude najít posloupnost otočení takovou, že Jirka během jízdy nespadne a zároveň celkový úhel, o který se bude muset v součtu otáčet, je nejmenší možný. Na vstupu dostaneme počet sil, velikost F₀, kterým směrem se Jirka dívá na počátku jízdy a následně pro každou sílu v průběhu jízdy její velikost a směr. Chceme vypsat součet úhlů, o který se bude muset Jirka v optimálním řešení otáčet.

Řešení

34-3-4 Horňáci a Dolňáci (12 bodů)

Hercule Poirot pozoruje dění v ospalém anglickém městečku. Obyvatelé se dělí na Horňáky a Dolňáky. Obě skupiny se navzájem nesnáší, takže když vidíte dva lidi hádat se na ulici, můžete si být jisti, že je to Horňák s Dolňákem.

Hercule si všechny hádky pečlivě zapisuje do notýsku. Když se večer vrátí do hostince, prochází záznamy a snaží se zjistit, kdo je Horňák a kdo Dolňák. „Sacrebleu!“, vykřikl Hercule, neboť zrovna zjistil, že pozorování nejsou konzistentní. Má podezření, že přes všechnu svou pečlivost si jeden záznam zapsal špatně. Přijďte na to, který záznam má Hercule škrtnout, aby zbylé záznamy jednoznačně určovaly rozdělení na obě skupiny.

Trochu formálněji: obyvatelé městečka jsou očíslovaní od 1 do N, přičemž číslo 1 odpovídá hostinskému, který je Horňák. Herculovy záznamy jsou uspořádané dvojice (x₁,y₁) až (x_M,y_M). Dvojice (x_i,y_i) popisuje, že obyvatelé s čísly x_i a y_i se někdy během dne pohádali. Výstupem vašeho algoritmu by měla být jedna dvojice, kterou je potřeba smazat.

Řešení

34-3-X1 Dráteníci (10 bodů)

Firma Dráteník a synové buduje počítačovou síť v Kráčmerově. Do jednoho domu umístili centrální router, ke kterému chtějí připojit všechny ostatní domy. Mezi domy již natahali trubky, které tak tvoří neorientovaný graf, a teď do nich budou zavlékat kabely. Každý dům má být připojen kabelem k centrálnímu routeru. Kabel povede posloupností trubek (po cestě v grafu) a není ho možné větvit.

Každý kabel má nějakou barvu. Aby byl v kabelech pořádek, smí být v jedné trubce více kabelů jen tehdy, mají-li různé barvy. Barev chceme ovšem použit co nejméně, protože růžové kabely se zlatými puntíčky se shání dost špatně …

Vymyslete algoritmus, který na vstupu dostane graf trubek mezi domy s vyznačeným routerem. Jeho výstupem bude zaprvé minimální možný počet barev, zadruhé pro každý vrchol grafu informace, jakou barvu drátu použít k jeho připojení a kudy kabel natáhnout. Pro každou hranu grafu přitom musí platit, že všechny dráty, které ji používají, mají různé barvy.

Nápověda

Protože se nikomu nepodařilo tuto úlohu vyřešit, rozhodli jsme se, že prodloužíme její deadline do konce 4. série. Navíc vydáváme následující nápovědu, která vám snad pomůže k řešení.

Při řešení této úlohy se vám můžou hodit algoritmy řešící problém toků v síti. Graf, který bude vstupem algoritmu na toky, nemusí nutně být ten, který je na vstupu úlohy. Například může být i mnohem větší.

Řešení

34-3-S Manimujeme – kamera a grafy (15 bodů)

Hlavní stránka dokumentace: https://docs.manim.community/en/stable/reference.html

Odkaz na Jupyter notebook tohoto dílu: https://mybinder.org/v2/gh/ksp/ksp-serial-34.git/HEAD?labpath=serial3.ipynb

save a restore

from manim import *

class SaveAndRestoreExample(Scene):
    def construct(self):
        square = Square()

        # uložení toho, jak aktualně čtverec vypadá
        square.save_state()

        self.play(Write(square))

        self.play(square.animate.set_fill(WHITE, 1))
        self.play(square.animate.scale(1.5).rotate(PI / 4))
        self.play(square.animate.set_color(BLUE))

        # navrácení do původního stavu
        self.play(square.animate.restore())

        # nová animace!
        self.play(Unwrite(square))

restore [doc] je jako vždy možné použít jak v animate syntaxu, tak bez něho.

Jednu animaci, kterou jsme ještě neviděli ale v kódu výše je použitá, je animace Unwrite [doc], která je pouze obrácená Write [doc]. Hodit se může obzvlášť při mizení textu a jednoduchých tvarů, jako byl čtverec v animaci výše.

Grafy

from manim import *

class GraphExample(Scene):
    def construct(self):
        # graf očekává vrcholy a hrany v tomto tvaru
        vertices = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
        edges = [
            (1, 2),
            (2, 3),
            (3, 4),
            (2, 4),
            (2, 5),
            (6, 5),
            (1, 7),
            (5, 7),
            (2, 8),
            (1, 9),
            (10, 8),
            (5, 11),
        ]

        # layout_config používáme k tomu, aby byl algoritmus nastavující pozice vrcholů
        # deterministický (ten defaultní potřebuje seed)
        g = Graph(vertices, edges, layout_config={"seed": 0}).scale(1.6)

        self.play(Write(g))

        # graf obsahuje updatery, aby se hrany posouvaly s vrcholy
        self.play(g.vertices[6].animate.shift((LEFT + DOWN) * 0.5))

        self.play(g.animate.shift(LEFT * 3))

        # grafy mohou rovněž obsahovat labely a mohou být uspořádány do jiných layoutů
        # (pro ukázku všech viz link na dokumentaci třídy v seriálu)
        h = Graph(vertices, edges, labels=True, layout="circular").shift(RIGHT * 3)

        self.play(Write(h))

        # pokud chceme větší vrcholy i bez labelů, tak si je musíme obstarat manuálně
        self.play(*[g.vertices[v].animate.scale(2.15) for v in g.vertices])

        # obarvíme vrchol 5 a jemu odpovídající hrany (může se hodit v jedné z úloh :)
        v = 5
        self.play(
            Flash(g.vertices[v], color=RED, flash_radius=0.5),
            g.vertices[v].animate.set_color(RED),
            *[g.edges[e].animate.set_color(RED) for e in g.edges if v in e],
        )

Jak je z ukázky vidět, třída očekává vstup jako seznam vrcholů a hran. Přistupovat k nim lze následně před slovníky vertices a edges – jen pozor na to, že pokud má graf uloženou hranu jako (v, w), tak přístup přes (w, v) nefunguje (což je u neorientovaných grafů vcelku nepraktické a neintuitivní).

Defaultní algoritmus k pozicování vrcholů je Fruchterman-Reingoldův a funguje na jednoduchém principu – vrcholy odpuzují a hrany přitahují. Kromě seed obsahuje řadu dalších parametrů (viz odkaz výše), které je možné přes slovník specifikovat.

Orientované grafy zatím knihovna nepodporuje (a nejspíš ještě nějakou dobu podporovat nebude).

K vytvoření náhodného grafu (pokud se nám ho nechce zadávat ručně) je možně použít knihovnu networkx, která obsahuje řadu šikovných generátorů grafů a jiných grafových funkcí:

from manim import *
from random import *
import networkx as nx

class GraphGenerationExample(Scene):
    def construct(self):
        seed(0xDEADBEEF)

        n = 12  # počet vrcholů
        p = 3 / n  # pravděpodobnost, že mezi dvěma vrcholy je hrana

        # generujeme, dokud nemáme spojitý graf
        graph = None
        while graph is None or not nx.is_connected(graph):
            graph = nx.generators.random_graphs.gnp_random_graph(n, p)

        g = (
            Graph(graph.nodes, graph.edges, layout_config={"seed": 0})
            .scale(2.2)
            .rotate(-PI / 2)
        )

        self.play(Write(g))

Kamera

Běžná třída Scene [doc] k měnící-se kameře však není uzpůsobená, proto místo ní budeme používat třídu MovingCameraScene [doc]. Ta nově obsahuje objekt frame, který lze animovat a posouvat tím kameru:

from manim import *

class MovingCameraExample(MovingCameraScene):
    def construct(self):
        square = Square()

        self.play(Write(square))

        # uložíme si stav kamery, protože s ní následně budeme pracovat
        self.camera.frame.save_state()

        # zoomneme tak, aby čtverec zaplňoval celý obraz (+ drobná mezera)
        self.play(self.camera.frame.animate.set_height(square.height * 1.5))

        circle = Circle().next_to(square, LEFT)

        # posunutí kamery k novému objektu (kruhu)
        self.play(
            AnimationGroup(
                self.camera.frame.animate.move_to(circle),
                Write(circle),
                lag_ratio=0.5,
            )
        )

        self.wait(0.5)

        # trošku odzoomujeme (zvětšení bude zabírat více scény)
        self.play(self.camera.frame.animate.scale(1.3))

        triangle = Triangle().next_to(square, RIGHT)

        # posunutí kamery k novému objektu (trojúhelníku)
        self.play(
            AnimationGroup(
                self.camera.frame.animate.move_to(triangle),
                Write(triangle),
                lag_ratio=0.5,
            )
        )

        self.wait(0.5)

        # navrácení kamery do původního stavu
        self.play(self.camera.frame.animate.restore())

Jak je z ukázky vidět, objekt self.camera.frame se chová stejně jako každý doposud animovaný objekt – můžeme nastavovat výšku, škálovat, posouvat, apod. To mimo jiné znamená, že můžeme používat updatery přesně tak, jak očekáváme:

from manim import *

class MovingCameraUpdaterExample(MovingCameraScene):
    def construct(self):
        seed(0xDEADBEEF)

        n = 11 ** 2

        circles = VGroup(
            *[
                Circle(radius=0.1)
                .scale(uniform(0.5, 2))
                .shift(UP * uniform(-3, 3) + RIGHT * uniform(-5, 5))
                .set_color(WHITE)
                for _ in range(n)
            ]
        )

        # kamerou budeme pozorovat kruh, který je v půlce
        target = circles[n // 2]

        def update_curve(camera):
            """Updater, který udržuje kameru nad cílem."""
            camera.move_to(target.get_center())

        self.camera.frame.add_updater(update_curve)

        # POZOR!
        # updatery fungují pouze na věci přidané na scénu
        # self.camera.frame na scéně nejprve není, je ho potřeba přidat
        self.add(self.camera.frame)

        self.play(FadeIn(circles))

        # animace pozicování kružnic a postupné Zoomování
        scale_factor = 0.7

        self.play(
            circles.animate.arrange_in_grid().set_color(RED),
            self.camera.frame.animate.scale(scale_factor),
            run_time=1.5,
        )

        self.play(
            circles.animate.arrange_in_grid(rows=5).set_color(GREEN),
            self.camera.frame.animate.scale(scale_factor),
            run_time=1.5,
        )

        self.play(
            circles.animate.arrange_in_grid(cols=14).set_color(BLUE),
            self.camera.frame.animate.scale(scale_factor),
            run_time=1.5,
        )

Jak je v kódu zmíněno, je potřeba si dávat velký pozor na to, zda je updatovaný objekt na scéně. V tomto případě ještě nebyl objekt animovaný, proto na scénu přidaný není (scéna updatuje pouze objekty, které v ní aktuálně jsou) a je potřeba ho manuálně přidat přes self.camera.frame. Pokud váš updater nic nedělá, tak je velká šance že updatovaný objekt není přidaný.

Kamera umí kromě pohybu a zoomování i další věci, jmenovitě například změnu barvy pozadí:

from manim import *

class BackgroundColorExample(MovingCameraScene):
    def construct(self):
        self.camera.background_color = WHITE
        self.camera.frame.scale(0.6)

        square = Square(color=BLACK)

        self.play(Write(square))

        circle = Circle(color=BLACK).next_to(square, LEFT)
        triangle = Triangle(color=BLACK).next_to(square, RIGHT)

        self.play(FadeIn(triangle, shift=RIGHT * 0.2), FadeIn(circle, shift=LEFT * 0.2))

Rate funkce

from manim import *

# Kód pochází z Manimové dokumentace (modulo drobné úpravy)
# https://docs.manim.community/en/stable/reference/manim.utils.rate_functions.html

class RateFunctionsExample(Scene):
    def construct(self):
        line1 = Line(3 * LEFT, RIGHT).set_color(RED)
        line2 = Line(3 * LEFT, RIGHT).set_color(GREEN)
        line3 = Line(3 * LEFT, RIGHT).set_color(BLUE)
        line4 = Line(3 * LEFT, RIGHT).set_color(ORANGE)

        lines = VGroup(line1, line2, line3, line4).arrange(DOWN, buff=0.8).move_to(LEFT * 2)

        dot1 = Dot().move_to(line1.get_start())
        dot2 = Dot().move_to(line2.get_start())
        dot3 = Dot().move_to(line3.get_start())
        dot4 = Dot().move_to(line4.get_start())

        dots = VGroup(dot1, dot2, dot3, dot4)

        # pozor na podtržítka při psaní TeXu
        label1 = Tex("smooth (default)").next_to(line1, RIGHT, buff=0.5)
        label2 = Tex("linear").next_to(line2, RIGHT, buff=0.5)
        label3 = Tex("there\_and\_back").next_to(line3, RIGHT, buff=0.5)
        label4 = Tex("rush\_into").next_to(line4, RIGHT, buff=0.5)

        labels = VGroup(label1, label2, label3, label4)

        self.play(Write(lines), FadeIn(dots), FadeIn(labels))

        # použití s animate syntaxem
        self.play(
            dot1.animate(rate_func=smooth).shift(RIGHT * 4),
            dot2.animate(rate_func=linear).shift(RIGHT * 4),
            dot3.animate(rate_func=there_and_back).shift(RIGHT * 4),
            dot4.animate(rate_func=rush_into).shift(RIGHT * 4),
            run_time=3,
        )

        self.play(FadeOut(lines), FadeOut(dots))

        # použití s normálními animacemi
        self.play(
            Write(line1, rate_func=smooth),
            Write(line2, rate_func=linear),
            Write(line3, rate_func=there_and_back),
            Write(line4, rate_func=rush_into),
            run_time=3,
        )

Níže je (ne)úplný list křivek, které se v animacích běžně používají. Rovněž existuje skvělá stránka, která řadu z těchto křivek obsahuje a umí interaktivně vizualizovat jejich průběh, pokud je nechcete zkoušet přímo v Manimu.

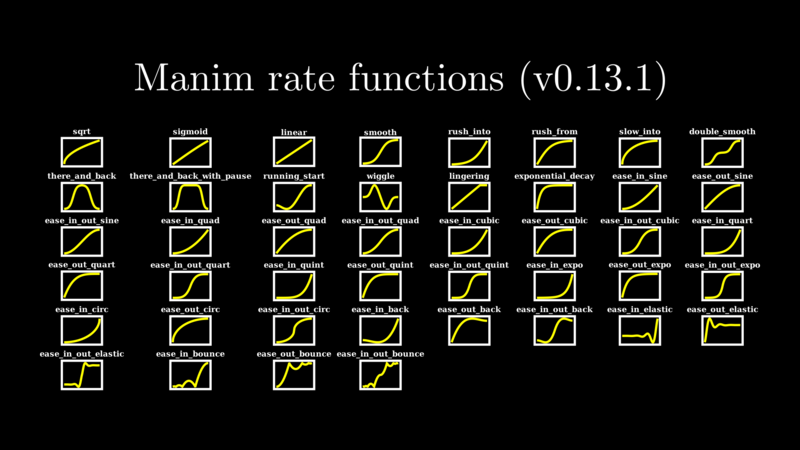
Krokování

from manim import *

class NextSectionExample(Scene):
    def construct(self):
        shapes = VGroup(Circle(), Square(), Triangle()).arrange()

        # jméno sekce je nepovinné a nemusí být unikátní
        # skip_animations animování sekce přeskočí
        self.next_section("vykreslení kruhu", skip_animations=True)

        self.play(Write(shapes[0]))

        self.next_section("vykreslení čtverce")

        self.play(Write(shapes[1]))

        self.next_section("vykreslení trojúhelníku")

        self.play(Write(shapes[2]))

Scény se dále hodí k pohodlnějšímu zpracování částí animace jinými programy (viz tento odkaz na Manim dokumentaci), jelikož Manim po vygenerování videa se sekcemi při použití vlajky --save_sections vygeneruje následný json soubor:

[
    {
        "name": "vykreslen\u00ed \u010dtverce",
        "type": "default.normal",
        "video": "NextSectionExample_0001.mp4",
        "codec_name": "h264",
        "width": 1920,
        "height": 1080,
        "avg_frame_rate": "60/1",
        "duration": "1.000000",
        "nb_frames": "60"
    },
    {
        "name": "vykreslen\u00ed troj\u00faheln\u00edku",
        "type": "default.normal",
        "video": "NextSectionExample_0002.mp4",
        "codec_name": "h264",
        "width": 1920,
        "height": 1080,
        "avg_frame_rate": "60/1",
        "duration": "1.000000",
        "nb_frames": "60"
    }
]

Úlohy

K odevzdávání úloh lze animaci vytvořit buď online přímo v Jupyteru pro tento díl (na konci dokumentu je kostra pro každou z úloh, do které ji jde přímo doprogramovat), nebo i lokálně, pokud máte nainstalovný Manim.

Odevzdávejte celý zdrojový kód v zazipovaném (a nezaheslovaném) archivu.

V každé z úloh tohoto i nadcházejících dílů je cílem naprogramovat animaci obecně, ne jen pro jeden vstup. Animace by za vás měl dělat nějaký algoritmus, rozhodně byste je neměli programovat manuálně (pohyb za pohybem).

Úkol 1 – Grafový algoritmus [5b]

Naprogramujte animaci DFS (nebo nějakého jiného pěkného grafového algoritmu):

Úkol 2 – Fibonacciho posloupnost [5b]

Naprogramujte animaci Fibonacciho posloupnosti (nebo nějaké jiné podobné posloupnosti, jako Pellovy a Lucasovy):

Velice se budou hodit updatery z předchozího dílu seriálu. Zároveň se bude hodit třída TracedPath [doc], která po přidání do scény trasuje určený objekt. Šikovná bude rovněž animace Rotate [doc], která umí rotovat objekt okolo nějakého jiného:

from manim import *

class TracePathExample(Scene):
    def construct(self):
        dot = Dot().shift(LEFT)

        self.play(Write(dot))

        # objekt TracedPath přijímá funkci, které se opakovaně ptá na pozici objektu, který sleduje
        # proto používáme dot.get_center, která vrací aktuální pozici tečky kterou tracujeme
        path = TracedPath(dot.get_center)

        # nesmíme zapomenout cestu přidat do scény, aby byla vykreslována!
        self.add(path)

        self.play(Rotate(dot, about_point=ORIGIN))

        self.play(dot.animate.shift(UP))
        self.play(dot.animate.shift(LEFT * 2))
        self.play(dot.animate.shift(DOWN))

        # pro zkončení tracování můžeme použít clear_updaters
        path.clear_updaters()

        self.play(dot.animate.shift(RIGHT * 2))

Je zde je však dobná zrada: používání TracedPath k přidávání do objektu tímto způsobem naráží v Manimu na známý bug s cachováním, proto je třeba při volání použít --disable_caching flag, který tento bug vyputím cachování obchází.

Úkol 3 – Langtonův mravenec [5b]

Naprogramujte animaci Langtonova mravence (nebo nějaké jeho barevné varianty). V každém kroku se mravenec posune následujícím způsobem:

• Pokud je na černém políčku, otočí se doprava, jinak se otočí doleva.
• Invertuje barvu políčka, na kterém stojí.
• Posune se dopředu.

K vytvoření mravence můžete použít SVGMobject [doc] (a například toto SVG mravence):

from manim import *

class SVGExample(Scene):
    def construct(self):
        image = SVGMobject("ant.svg")

        self.play(Write(image))

        self.play(image.animate.set_color(RED).scale(1.75))

        self.play(Rotate(image, TAU))  # tau = 2 pi

        self.play(FadeOut(image))

Tomáš Sláma

Řešení