Čtvrtá série třicátého čtvrtého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám čtvrté číslo hlavní kategorie 34. ročníku KSP.

Opět se můžete těsit na dvě praktické a dvě teoretické úlohy. Tentokrát nepřidáváme žádnou těžší úlohu kategorie X, protože na úlohu 34-3-X1 z minulé série nám nepřišlo žádné správné řešení. Tak jsme její termín prodloužili do konce této série a přidali nápovědu do jejího zadání. Nakonec je zde tradičně pokračování Manimového seriálu, tentokrát s podtitulem 3D.

Odměny & na Matfyz bez přijímaček

• Termín série: neděle 10. dubna ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Každému, kdo z této série získá alespoň 42 bodů, pošleme sladkou odměnu.

Zadání úloh

• 34-4-1: No pun indented!
• 34-4-2: Písemka z analýzy
• 34-4-3: Korelace nejsou tranzitivní
• 34-4-4: Geometrie
• 34-4-S: Manimujeme – 3D a grafy

34-4-1 No pun indented! (9 bodů)

Kristýna právě napsala řešení úložky z KSP-X v Pythonu. Ovšem stalo se nemyslitelné. Její oblíbený editor (který si sama napsala předchozí noc) jí při ukládání souboru smazal všechny mezery na začátku řádků. Co teď s tím? pomyslela si Kristýna. Psát znovu se mi to nechce, tak přeci nemůže být tolik možností, jak doplnit mezery, aby se jednalo o validní Python. Projdu všechny a vyzkouším, která z nich na zadaných vstupech funguje.

Ukažte, že se Kristýna mýlí, a zjistěte, že pro její kód je více validních odsazení, než zvládne vyzkoušet do termínu úlohy. Spočítejte, kolik takových odsazení je.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Na vstupu je nejprve číslo N, následuje N řádků programu. Řádky na svém začátku ani konci nemají mezery (uprostřed však být mohou) a každý obsahuje alespoň jeden znak. Na každém řádku je buď řídící příkaz nebo normální příkaz. Řádky řídících příkazů (jako například cykly, podmínky, definice funkcí, …) se poznají tak, že končí dvojtečkou.

První příkaz v programu nesmí mít žádné odsazení. Ve validním programu musí za každým řídícím příkazem následovat řádek s o jedna vyšším odsazením. Za normálním příkazem se nesmí velikost odsazení zvýšit. Může ovšem zůstat stejná nebo se snížit, a to o libovolně mnoho úrovní. Je zaručeno, že poslední řádek na vstupu není řídící příkaz.

Za validní programy považujeme všechny takové, které splňují výše popsané podmínky. Neřešíme jiná pravidla platná v Pythonu, například jestli jsou splněny vztahy mezi řídícími příkazy, nebo jestli jsou v daném odsazení definované všechny identifikátory. Kristýna totiž i takovéto programy vyzkouší spustit a až pak zjistí, že program spadne.

Jako výstup odevzdejte počet validních odsazení. Protože toto číslo může snadno narůst, tak na výstup vypište jeho zbytek po dělení 10⁹+7 (což je šikovně velké prvočíslo). Zbytek po dělení doporučujeme aplikovat už v průběhu výpočtu při sčítání a násobení, výsledek to nezmění a zabrání to přetečení datového typu.

12
#!/usr/bin/env python3
from random import *
seed(42)
print(100)
for i in range(100):
try:
s = "".join(choice("abc") for i in range(10))
finally:
if random()<0.4:
print(s+":")
elif True:
print(s)

12

I když jen jeden způsob odsazení vytvoří skutečně validní Python, naší definici vyhoví 12 různých odsazení. Kdybychom si vzali onen validní Pythoní kód a spustili jej, všimneme si, že by opět vytvořil zadání pro tuto úlohu. Prozradíme, že na něj by správná odpověď byla 792 306 071.

Řešení

34-4-2 Písemka z analýzy (10 bodů)

Profesor Nilpferd učí matematickou analýzu a neustále udržuje své studenty ve střehu nenadálými písemkami. Studenti vymýšlejí čím dál šílenější hypotézy (hippotézy?) o tom, jak se rozhoduje, kdy písemku zadá a kdy ne. Alice si je jistá, že je to podle fáze měsíce. Bob má podezření na večerní červánky. Podle Cyrila se zaručeně řídí ligou ve famfrpálu.

Každý večer se zeptáte svých spolužáků. Každý řekne svůj názor na to, zda bude zítra písemka. Vy si na základě vyslechnutých tipů vytvoříte vlastní názor a podle něj jdete buďto klidně spát, nebo se začnete na zítřek zuřivě učit. Dopoledne se dozvíte, zda písemka nastala nebo ne. Podle toho můžete upravit, jak se budete další večer chovat. Toto se opakuje každý den v semestru.

Svou předpověď můžete popsat algoritmem. Ten každý den dostane všech n tipů spolužáků, vydá předpověď, a pak se dozví, jestli se vyplnila. Podle toho si upraví svůj vnitřní stav pro další den (například názor na to, jak dobrý je tip kterého spolužáka).

Myslíte si, že mezi spolužáky je alespoň jeden, který uhodl, jak se profesor rozhoduje, a tím pádem tipuje vždy správně. Jen vědět, kdo to je…

Vymyslete co nejlepší předpovědní algoritmus, tedy takový, který za těchto předpokladů udělá co nejméně chyb v závislosti na počtu spolužáků n a počtu dní semestru d. Snažte se minimalizovat počet chyb v nejhorším případě. Můžete předpokládat, že d je mnohem větší než n. Časová složitost algoritmu nás nezajímá.

Řešení

34-4-3 Korelace nejsou tranzitivní (11 bodů)

Ondra si nedávno přečetl dvě studie – že čím více lidé pijí mléko, tím vyšší v průměru jsou, a že vyšší lidé jsou v průměru úspěšnější. Nyní přemýšlí, jestli by neměl začít pít více mléka.

Je na vás, abyste mu vysvětlili, že takové uvažování nedává smysl. Nejen že korelace neimplikuje kauzalitu, ale to, že spolu něco koreluje, vůbec není tranzitivní. Je klidně možné, že čím více lidé pijí mléko, tím jsou v průměru méně úspěšní!

Máte k dispozici m studií, kde každá ukazuje silnou korelaci mezi dvěma veličinami (např. čím více lidé pijí mléko, tím jsou v průměru úspěšnější), a vaším cílem je najít posloupnost korelujících veličin takovou, že skončíte u negace první veličiny, abyste demonstrovali, že korelace nejsou tranzitivní.

Například posloupnost:

• čím jsou lidé bohatší, tím více peněz utrácí za víno,
• čím více peněz utrácí za víno, tím více vína pijí,
• čím více vína pijí, tím více alkoholu konzumují,
• čím více alkoholu konzumují, tím jsou méně bohatí,

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete počet veličin n, kterých se studie týkají, a počet studií m. Na každém z následujících m řádků bude trojice x_i, y_i a k_i, kde x_i a y_i udává, kterých dvou veličin se studie týká, a k_i je vždy buď 1 nebo -1, což udává, kterým směrem byla korelace naměřena. Číslo 1 odpovídá kladné korelaci (například čím jsou lidé bohatší, tím více peněz utrácí za víno) a -1 záporné korelaci (například čím lidé více konzumují alkohol, tím jsou méně bohatí).

Uvedené korelace jsou obousměrné. Pokud x koreluje s y, koreluje také y s x, a to se stejným znaménkem.

Platí, že 0 ≤ x_i, y_i < n (veličiny číslujeme od nuly), ∀i: x_i ≠ y_i a neexistují dvě různé studie, které by se týkaly stejné dvojice veličin.

Formát výstupu: První řádek výstupu bude obsahovat počet veličin ve vašem cyklu. Na dalším řádku pak budou tyto veličiny. Musí platit, že mezi každými dvěma sousedními veličinami existuje studie a poslední veličina v je rovná té první. Navíc musí posloupnost korelací vyjadřovat, že čím více v, tím méně v.

Pokud existuje více řešení, vypište libovolné.

4 5
0 3 -1
2 3 -1
1 2 1
1 0 -1
2 0 1

5
0 3 2 1 0

Řešení

34-4-4 Geometrie (15 bodů)

Jirka upekl dort a chtěl se o něj podělit se svými kamarády. Jelikož to není žádný cukrář, tak jeho dort měl poměrně neobvyklý nepravidelný tvar. Dokonce ani nebyl konvexní. Říkal si, že že by této vlastnosti dortu mohl využít. Rád by dort rozdělil na co nejvíce částí (neví totiž, kolik jeho kamarádů ještě dorazí) za použití pouze jednoho řezu.

Na vstupu jsou souřadnice N bodů nekonvexního N-úhelníku. Můžete předpokládat, že žádné tři body nejsou kolineární, tedy neleží na jedné přímce, a žádné dva body nemají shodnou ani jednu ze souřadnic.

Popište algoritmus, který spočítá, na kolik částí lze rozdělit N-úhelník pouze za pomoci jednoho řezu přímkou.

Lehčí varianta (za 8 bodů): Pro zisk části bodů můžete předpokládat, že optimální řez je rovnoběžný s osou x.

Řešení

34-4-S Manimujeme – 3D a grafy (15 bodů)

Hlavní stránka dokumentace: https://docs.manim.community/en/stable/reference.html

Odkaz na Jupyter notebook tohoto dílu: https://mybinder.org/v2/gh/ksp/ksp-serial-34.git/HEAD?labpath=serial4.ipynb

Binární operace

from manim import *

class BooleanOperations(Scene):
    def construct(self):

        circle = Circle(fill_opacity=0.75, color=RED).scale(2).shift(LEFT * 1.5)
        square = Square(fill_opacity=0.75, color=GREEN).scale(2).shift(RIGHT * 1.5)

        group = VGroup(circle, square)

        self.play(Write(group))

        self.play(group.animate.scale(0.5).shift(UP * 1.6))

        union = Union(circle, square, fill_opacity=1, color=BLUE)

        # postupně voláme Union(), Intersection() a Difference()
        for operation, position, name in zip(
            [Intersection, Union, Difference],
            [LEFT * 3.3, ORIGIN, RIGHT * 4.5],
            ["Průnik", "Sjednocení", "Rozdíl"],
        ):
            result = operation(circle, square, fill_opacity=1, color=DARK_BLUE)
            result_position = DOWN * 1.3 + position
            
            label = Tex(name).move_to(result_position).scale(0.8)
            
            self.play(
                AnimationGroup(
                    FadeIn(result),
                    result.animate.move_to(result_position),
                    FadeIn(label),
                    lag_ratio=0.5,
                )
            )

Při používání si je třeba dát pozor na to, že operace jsou omezené na vektorové objekty (VMobject [doc]) s nenulovou plochou. Průnik objektů jako úseček tedy neprodukuje bod (i když by geometricky měl).

Vlastní objekty

from manim import *

class Stack(VMobject):
    def __init__(self, size, *args, **kwargs):
        # inicializace VGroup objektu
        super().__init__(**kwargs)

        self.squares = VGroup()
        self.labels = VGroup()
        self.index = 0
        self.pointer = Arrow(ORIGIN, UP * 1.2)

        for _ in range(size):
            self.squares.add(Square(side_length=0.8))

        self.squares.arrange(buff=0.15)

        self.pointer.next_to(self.squares[0], DOWN)
        self.add()

        # DŮLEŽITÉ - přidáme do objektu všechny podobjekty!
        self.add(self.squares, self.labels, self.pointer)

    def __get_index_rectangle_color(self):
        """Vrátí barvu aktuálního obdelníků stacku."""
        return self.squares[self.index].get_color()

    def __create_label(self, element):
        """Vytvoření labelu daného prvku (podle barvy a rozměrů čtverců stacku)."""
        return (
            Tex(str(element))
            .scale(self.squares[0].height)
            .set_color(self.__get_index_rectangle_color())
        )

    def push(self, element):
        """Přidá prvek do zásobníku. Vrátí odpovídající animace."""
        self.labels.add(self.__create_label(element).move_to(self.squares[self.index]))
        self.index += 1

        return AnimationGroup(
            FadeIn(self.labels[-1]),
            self.pointer.animate.next_to(self.squares[self.index], DOWN),
            Indicate(
                self.squares[self.index - 1], color=self.__get_index_rectangle_color()
            ),
        )

    def pop(self):
        """Odebere prvek ze zásobníku. Vrátí odpovídající animace."""
        label = self.labels[-1]
        self.labels.remove(label)
        self.index -= 1

        return AnimationGroup(
            FadeOut(label),
            self.pointer.animate.next_to(self.squares[self.index], DOWN),
            Indicate(
                self.squares[self.index],
                color=self.__get_index_rectangle_color(),
                scale_factor=1 / 1.2,
            ),
        )

    def clear(self):
        """Vyčistí zásobník. Vrátí odpovídající animaci."""
        result = AnimationGroup(*[self.pop() for _ in range(self.index)], lag_ratio=0)

        self.index = 0

        return result

class StackExample(Scene):
    def construct(self):
        stack = Stack(10)

        # na objekt fungují správně libovolné animace
        self.play(Write(stack))

        self.wait(0.5)

        for i in range(5):
            self.play(stack.push(i))

        self.play(stack.pop())

        self.wait(0.5)

        # můžeme používat i animate syntax!
        # měnění barvy se rekurzivně aplikuje na všechny podobjekty
        self.play(stack.animate.scale(1.3).set_color(BLUE))

        self.wait(0.5)

        for i in range(2):
            self.play(stack.push(i))

        self.play(stack.pop())

        self.play(stack.clear())

        self.play(FadeOut(stack))

Grafy (ty druhé)

Nejjednodušší způsob zadefinování grafu je podle předpisu funkce:

from manim import *
from math import sin

class GraphExample(Scene):
    def construct(self):
        # osy - rozmezí a značení os x, y
        axes = Axes(x_range=[-5, 5], y_range=[-3, 7])
        labels = axes.get_axis_labels(x_label="x", y_label="y")

        def f1(x):
            return x ** 2

        def f2(x):
            return sin(x)

        # objekty vykreslených funkcí
        g1 = axes.plot(f1, color=RED)
        g2 = axes.plot(f2, color=BLUE)

        self.play(Write(axes), Write(labels))

        self.play(AnimationGroup(Write(g1), Write(g2), lag_ratio=0.5))

        self.play(Unwrite(axes), Unwrite(labels), Unwrite(g1), Unwrite(g2))

Při vykreslování grafů tímto způsobem je třeba si dát pozor na to, aby byly funkce spojité (a pokud nejsou, tak je třeba je vykreslit po spojitých částech). Je to kvůli tomu, že je Manim vykresluje počítáním mnoha funkčních hodnot, kterými prokládá křivku (polynom stupně určeného počtem bodů), a nemá tak šanci poznat, zda je skok způsobený tím, že se funkce mění spojitě, nebo nespojitě:

from manim import *
from math import sin

class DiscontinuousGraphExample(Scene):
    def construct(self):
        axes = Axes(x_range=[-5, 5], y_range=[-3, 7])
        labels = axes.get_axis_labels(x_label="x", y_label="y")

        def f(x):
            return 1 / x

        g_bad = axes.plot(f, color=RED)

        # rozdělení na dvě části podle hodnot x
        g_left = axes.plot(f, x_range=[-5, -0.1], color=GREEN)
        g_right = axes.plot(f, x_range=[0.1, 5], color=GREEN)

        self.play(Write(axes), Write(labels))

        self.play(Write(g_bad))
        self.play(FadeOut(g_bad))

        self.play(AnimationGroup(Write(g_left), Write(g_right), lag_ratio=0.5))

        self.play(Unwrite(axes), Unwrite(labels), Unwrite(g_left), Unwrite(g_right))

Další, obecnější možnost jak definovat graf je parametricky – rovněž zde definujeme předpis, ale jedná se o funkci jednoho parametru vracející souřadnice k vykreslení:

from manim import *
from math import sin, cos

class ParametricGraphExample(Scene):
    def construct(self):
        axes = Axes(x_range=[-10, 10], y_range=[-5, 5])
        labels = axes.get_axis_labels(x_label="x", y_label="y")

        def f1(t):
            """Parametrická funkce kružnice."""
            return (cos(t) * 3 - 4.5, sin(t) * 3)

        def f2(t):
            """Parametrická funkce <3."""
            return (
                0.2 * (16 * (sin(t)) ** 3) + 4.5,
                0.2 * (13 * cos(t) - 5 * cos(2 * t) - 2 * cos(3 * t) - cos(4 * t)),
            )

        # objekty vykreslených funkcí
        # místo axes.plot používáme axes.plot_parametric_curve
        # parametr t_range určuje, jaké je rozmezí parametru t
        g1 = axes.plot_parametric_curve(f1, color=RED, t_range=[0, 2 * PI])
        g2 = axes.plot_parametric_curve(f2, color=BLUE, t_range=[-PI, PI])

        self.play(Write(axes), Write(labels))

        self.play(AnimationGroup(Write(g1), Write(g2), lag_ratio=0.5))

        self.play(Unwrite(axes), Unwrite(labels), Unwrite(g1), Unwrite(g2))

Kromě definování grafů přes funkce je rovněž lze definovat přes samotné hodnoty jako úsečkové:

from manim import *
from random import random, seed

class LineGraphExample(Scene):
    def construct(self):
        seed(0xDEADBEEF2)  # hezčí hodnoty :P

        # hodnoty ke grafování (x a y)
        # u np.arange(l, r, step) vrátí pole hodnot od l do r (nevčetně) s kroky velikosti step
        x_values = np.arange(-1, 1 + 0.25, 0.25)
        y_values = [random() for _ in x_values]

        # osy (tentokrát s čísly)
        axes = Axes(
            x_range=[-1, 1, 0.25],
            y_range=[-0.1, 1, 0.25],
            # nastavení čísel - hodnoty a počet desetinných míst
            x_axis_config={"numbers_to_include": x_values},
            y_axis_config={"numbers_to_include": np.arange(0, 1, 0.25)},
            axis_config={"decimal_number_config": {"num_decimal_places": 2}},
        )

        labels = axes.get_axis_labels(x_label="x", y_label="y")

        # místo axes.plot používáme axes.plot_line_graph
        graph = axes.plot_line_graph(x_values=x_values, y_values=y_values)

        self.play(Write(axes), Write(labels))

        self.play(Write(graph), run_time=2)

        self.play(Unwrite(axes), Unwrite(labels), Unwrite(graph))

Úvod do 3D

V první řadě získáváme novou dimenzi, kterou značíme Z. Pro tuto novou dimenzi získáváme dvě nové konstanty, díky kterým se po ní můžeme posouvat: OUT (kladný směr) a IN (záporný směr). K tomu, aby Manim scénu správně renderoval, použijeme třídu ThreeDScene [doc]:

from manim import *

class Axes3DExample(ThreeDScene):
    def construct(self):
        # 3D osy
        axes = ThreeDAxes()
        
        x_label = axes.get_x_axis_label(Tex("x"))
        y_label = axes.get_y_axis_label(Tex("y")).shift(UP * 1.8)

        # 3D varianta Dot() objektu
        dot = Dot3D()
        
        # zmenšení zoomu, abychom viděli osy
        self.set_camera_orientation(zoom=0.5)

        self.play(FadeIn(axes), FadeIn(dot), FadeIn(x_label), FadeIn(y_label))
        
        self.wait(0.5)
        
        # animace posunutí kamery tak, aby byly osy dobře vidět
        self.move_camera(phi=75 * DEGREES, theta=30 * DEGREES, zoom=1, run_time=1.5)

        # vestavěný updater, který kameru začne rotovat (aby na scénu bylo lépe vidět)
        self.begin_ambient_camera_rotation(rate=0.15)

        # jedna tečka za každý směr
        upDot = dot.copy().set_color(RED)
        rightDot = dot.copy().set_color(BLUE)
        outDot = dot.copy().set_color(GREEN)

        self.wait(1)
        
        self.play(
            upDot.animate.shift(UP),
            rightDot.animate.shift(RIGHT),
            outDot.animate.shift(OUT),
        )
        
        self.wait(2)

Jak je v kódu vidět, výchozí pozice kamery je nastavená tak, aby pohled na scénu byl z 2D. K jejímu ovládání používáme set_camera_orientation [doc] pro nastavení pozice, move_camera [doc] pro animaci nastavení pozice a begin_ambient_camera_rotation [doc] pro nastavení konstantního otáčení kamery. Použité parametry phi (φ) a theta (ϑ) určují pozici kamery následně:

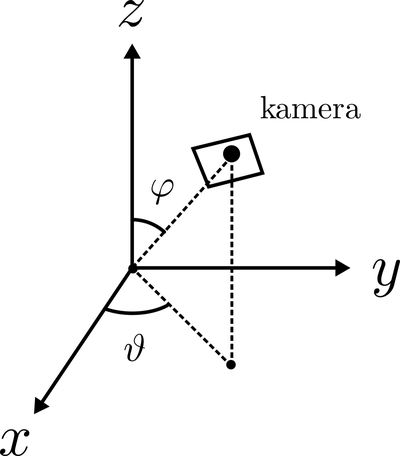
Kromě objektu ThreeDAxes [doc] obsahuje Manim řadu tříd a funkcí pro běžné objekty ve 3D, viz [doc]:

from manim import *

class Rotation3DExample(ThreeDScene):
    def construct(self):
        # přidání jednoduché základní krychle
        cube = Cube(side_length=3, fill_opacity=1)

        self.begin_ambient_camera_rotation(rate=0.3)

        # posunutí orientace kamery bez animace
        self.set_camera_orientation(phi=75 * DEGREES, theta=30 * DEGREES)

        self.play(Write(cube), run_time=2)

        self.wait(3)

        self.play(Unwrite(cube), run_time=2)

Posouvání a škálování objektů se ve 3D chová intuitivně (opět použijeme shift a scale). S otáčením je to trochu komplikovanější – ve 2D nám stačí fixovat bod okolo kterého budeme otáčet o daný úhel, ale jak by se objekt otáčel ve 3D? Otáčení ve 3D je zajímavý problém, který má různá řešení (pro zvídavé viz Eulerovy úhly a Kvaterniony). Nám bude stačit upřesnit osu, o kterou budeme daný objekt otáčet, čímž již operaci zjednoznačníme:

from manim import *

class Basic3DExample(ThreeDScene):
    def construct(self):
        # přidání jednoduché základní krychle
        cube = Cube(side_length=3, fill_opacity=0.5)

        self.set_camera_orientation(phi=75 * DEGREES, theta=30 * DEGREES)

        self.play(FadeIn(cube))

        for axis in [RIGHT, UP, OUT]:
            self.play(Rotate(cube, PI / 2, about_point=ORIGIN, axis=axis))

        self.play(FadeOut(cube))

Úlohy

K odevzdávání úloh lze animaci vytvořit buď online přímo v Jupyteru pro tento díl (na konci dokumentu je kostra pro každou z úloh, do které ji jde přímo doprogramovat), nebo i lokálně, pokud máte nainstalovaný Manim.

Odevzdávejte celý zdrojový kód v zazipovaném (a nezaheslovaném) archivu.

V každé z úloh tohoto i nadcházejících dílů je cílem naprogramovat animaci obecně, ne jen pro jeden vstup. Animace by za vás měl dělat nějaký algoritmus, rozhodně byste je neměli programovat manuálně (pohyb za pohybem).

Úkol 1 – Simulace binomického rozložení [6b]

Naprogramujte simulaci Galtonovy desky (a odpovídajícího grafu výsledků):

K pohybu kuličky budeme potřebovat několik nových tříd. V první řadě to bude třída CubicBezier [doc], podle které můžeme modelovat křivku, po které bude kulička putovat. K samotné animaci pohybu použijeme funkci MoveAlongPath [doc]. Pro zkombinování posunu s mizením můžeme použít vlastní animaci MoveAndFade, kterou prozatím považujte za magickou – v příštím díle seriálu si vytváření vlastních animací objasníme. Rovněž se budou hodit některé rate funkce z minulého dílu seriálu, aby pohyb po křivce vypadal správně:

from manim import *
from random import choice, seed

class MoveAndFade(Animation):
    def __init__(self, mobject: Mobject, path: VMobject, **kwargs):
        self.path = path
        self.original = mobject.copy()
        super().__init__(mobject, **kwargs)

    def interpolate_mobject(self, alpha: float) -> None:
        point = self.path.point_from_proportion(self.rate_func(alpha))

        # tohle není úplně čisté, jelikož pokaždé vytváříme nový objekt
        # je to kvůli tomu, že obj.fade() nenastavuje průhlednost ale přidává jí
        self.mobject.become(self.original.copy()).move_to(point).fade(alpha)

class BezierExample(Scene):
    def construct(self):
        # křivku definujeme přes čtyři body:
        # 2 krajní, ve kterých začíná a končí
        # 2 kontrolní, které určují tvar
        positions = [
            UP + LEFT * 3,  # počáteční
            UP + RIGHT * 2,  # 1. kontrolní
            DOWN + LEFT * 2,  # 2. kontrolní
            DOWN + RIGHT * 3,  # koncový
        ]

        points = VGroup(*[Dot().move_to(position) for position in positions]).scale(1.5)

        # rozlišíme kontrolní body
        points[1].set_color(BLUE)
        points[2].set_color(BLUE)

        bezier = CubicBezier(*positions).scale(1.5)

        self.play(Write(bezier), Write(points))

        # animace posunu
        circle = Circle(fill_opacity=1, stroke_opacity=0).scale(0.25).move_to(points[0])

        self.play(FadeIn(circle, shift=RIGHT * 0.5))
        self.play(MoveAlongPath(circle, bezier))

        self.play(FadeOut(circle))

        # animace posunu s mizením
        circle = (
            Circle(fill_color=GREEN, fill_opacity=1, stroke_opacity=0)
            .scale(0.25)
            .move_to(points[0])
        )

        self.play(FadeIn(circle, shift=RIGHT * 0.5))
        self.play(MoveAndFade(circle, bezier))

        self.play(FadeOut(bezier), FadeOut(points), FadeOut(circle))

Pokud by vás zajímalo, jak přesně se tato křivka chová pro různé pozice bodů (nebo případně jak matematicky funguje), tak velice doporučuji tuto interaktivní stránku, která vše elegantně vysvětluje.

3D Game of Life

Naprogramujte různé verze Conwayovy hry života (viz zadání níže). U každé prosím odevzdávejte i vygenerovaná videa.

Princip hry je následující – začínáme v počátečním stavu, ve kterém jsou nějaké buňky živé a nějaké mrtvé. Každá (až na krajní) má 26 sousedů (všechny buňky ve vzdálenosti 1 v prostoru). Pro danou hru definujeme množiny X a Y, které určují, zda buňky budou živé nebo mrtvé. V každém kroku se všechny buňky najednou změní podle následujících pravidel:

• Pokud je buňka živá a má počet sousedů v X, tak přežije , jinak zemře .
• Pokud je buňka mrtvá a má počet sousedů v Y, tak ožije , jinak zůstane mrtvá .

Úkol 2 [5b]

Uvažme hru X = {4, 5} a Y = {5}. Její 16×16 simulace s náhodným počátečním stavem (živé buňky s p = 0.2) a barvami určenými pozicí ve 3D prostoru bude vypadat následně:

Naprogramujte výše popsanou hru. Jako kontrolu správnosti animace můžete použít tento interaktivní editor.

Velice doporučuji nejprve renderovat menší vstupy (např. 8×8) a menší detaily a snímky za vteřinu (l). Manim sice renderování 3D podporuje, ale není na to optimalizovaný – používá pouze procesor, který je na animace tohoto typu řádově pomalejší než grafická karta. Pokud máte zájem o rychlejší renderování, doporučuji prozkoumat ManimGL, který je aktivně vyvíjen Grantem Sandersonem (3b1b) a podporuje interaktivní animace, ale má prakticky neexistující dokumentaci a v mnoha věcech se od seriálem používané verze liší.

Úkol 3 [3b]

Definujme parametr Z, který určuje životnost buňky. Životnost nové buňky je Z, přičemž se při každém kroku sníží o 1. Buňka může nyní zemřít pouze pokud je její životnost 1, jinak je považována za živou. Pokud při životnosti 1 přežije, tak její životnost zůstává 1.

Naprogramujte hru X = {2, 6, 9}, Y = {4, 6, 8, 9}, Z = 10. Barvy jsou určeny podle stáří buňky.

Úkol 4 [1b]

Najděte nějaké další zajímavé pravidlo (a počáteční stav, ať už náhodný nebo daný).

Jako inspiraci můžete použít tento zajímavý článek, který několik dalších pravidel ukazuje, jen je prosím nepoužívejte přímo.

Tomáš Sláma

Řešení