Čtvrtá série třicátého čtvrtého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 34-4-1: No pun indented!
- 34-4-2: Písemka z analýzy
- 34-4-3: Korelace nejsou tranzitivní
- 34-4-4: Geometrie
- 34-4-S: Manimujeme – 3D a grafy
34-4-1 No pun indented! (Zadání)
Počet validních odsazení budeme počítat postupně pro každý prefix (Prefix je posloupnost prvních několika řádků.) řádků a každou úroveň odsazení posledního z nich.
Pro první řádek existuje pouze jediný způsob, jak jej odsadit – nemůžeme jej odsadit vůbec, protože se zatím určitě nenacházíme za žádným řídicím příkazem.
Nyní si představme, že jsme již spočítali všechny možné způsoby, kterými lze odsadit prvních i řádků. Jak můžeme z tohohle počtu vyjít, aby se nám podařilo zjistit možnosti také pro prvních i+1 řádků?
Zkusíme každou z těchto možností vzít a vyzkoušet pro ni, zda může být (i+1)-ní řádek odsazen o 0, 1, … úrovní tak, aby vzniklý kód byl validně odsazen. Maximální úroveň odsazení je rovna počtu řídicích příkazů, jejich počet můžeme shora odhadnout počtem řádků na vstupu, tedy N. To je sice nadsazený odhad, ovšem řádově jich tolik být může, asymptotickou složitost ani správnost řešení to tedy neovlivní.
Všimneme si, že pokud je prvních i řádků již validně odsazeno, nemusíme znovu procházet celý kód. Stačí nám pouze zkontrolovat, zda je (i+1)-ní řádek správně odsazen vzhledem k i-tému řádku.
Řekněme, že (i+1)-ní řádek má mít odsazení úrovně ℓ. Jaká všechna odsazení mu mohou předcházet?
Musíme rozlišit dvě situace:
- Na i-tém řádku se nachází řídicí příkaz: Úroveň odsazení i-tého řádku může být jedině ℓ-1.
- Na i-tém řádku se nachází normální příkaz: Odsazení i-tého řádku může být úrovně ℓ, … , N.
Abychom tedy správně spočítali všechny možnosti odsazení prvních i+1 řádků, musíme si také pamatovat, kolika způsoby lze odsadit prvních i řádků pro konkrétní úroveň odsazení i-tého řádku.
Zkusíme námi odvozený vztah ještě vyjádřit vzorcem. Nechť C[i][k] značí počet možností odsazení prvních i řádků kódu, přičemž i-tý řádek má mít k-tou úroveň odsazení.
Potom speciálně platí:
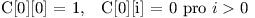
Jinak obecně platí:
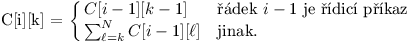
Odpověď se potom skrývá v hodnotě C[N][0] – do ní totiž bude posčítaný celý poslední řádek
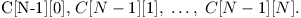
Časová složitost řešení záleží na tom, jakým způsobem hodláme počítat součet možností na řádku, kterému předchází normální příkaz. Pokud si součet rozepíšeme, můžeme si všimnout, že
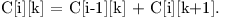
Jelikož nám ke spočtení kombinací pro každý následující řádek stačí vycházet pouze z hodnot v předchozím řádku, můžeme si udržovat pouze dvě pole o velikosti O(N), jejichž obsahy budeme po zpracování každého řádku prohazovat.
Pokud navíc budeme dostatečně opatrní v přepisování počítaných hodnot, vystačíme si dokonce s jediným polem. Celková paměťová složitost našeho řešení v obou případech bude O(N).
34-4-2 Písemka z analýzy (Zadání)
Budeme si udržovat množinu M spolužáků, kteří ještě neudělali chybu. Každý den se jich zeptáme a vybereme si tu odpověď, kterou řekla většina. Bude-li to půl na půl, zvolíme libovolně.
Pokaždé, když se naše předpověď nevyplní, odstraníme z M všechny spolužáky, kteří předpovídali špatně. Jelikož jsme se řídili většinou, množina M se zmenší alespoň dvakrát.
Ukážeme, že tato strategie udělá nejvýš log2 n chyb, kde n je počet spolužáků. Na počátku jsou v M všichni spolužáci, po k chybách klesne velikost M na nejvýše n/2k. Kdyby nastalo k> log2 n, musela by M už být prázdná. To ale není možné, protože vždy v ní zůstane aspoň ten jeden spolužák, který se nikdy nemýlí.
Náš příběh o písemce z analýzy je zjednodušenou verzí úlohy známé pod názvem
The Experts Problem. V té místo spolužáka, který se nikdy nemýlí, existuje
takový, jenž chybuje maximálně c-krát. Pojďme vyřešit i tuto verzi.
Už nefunguje přestat se ptát spolužáků poté, co se zmýlili. Místo toho si u každého spolužáka budeme udržovat nějakou váhu mezi 0 a 1. Ta vyjadřuje, jak moc mu věříme. Vždy se zeptáme všech a zvolíme tu odpověď, kterou nám dali spolužáci s vyšší celkovou vahou. Pokud tato předpověď nevyšla, pak těm spolužákům, kteří se nestrefili, vydělíme váhu dvěma.
Označme W součet všech vah a počítejme, jak se v průběhu semestru mění. Na počátku má každý spolužák váhu 1, takže W=n. Pokud písemku předpovíme správně, W se nezmění. Pokud špatně, spolužákům o celkové váze aspoň W/2 vydělíme váhu dvěma, takže celkovou váhu snížíme o aspoň W/4. Nová celková váha tedy bude nejvýš 3/4·W. Obecně po k chybách máme W ≤ n·(3/4)k.
Na druhou stranu víme, že existuje spolužák, který udělá nejvýš c chyb. Jeho váha proto nikdy neklesne pod 2-c, takže bude vždy platit W≥ 2-c.
Teď už stačí obě nerovnosti pro W spojit. Dostaneme:
Obě strany nerovnosti zlogaritmujeme:
Přehodíme log2 n na druhou stranu:
Nakonec si uvědomíme, že log2(3/4) ≐-0.415 ≐-1 / 2.409. Když tímto číslem vydělíme obě strany, otočí se nerovnost a dostaneme:
Uděláme tedy pouze O(c + log n) chyb.
Konstanta 2.41 by se jestě dala vylepšovat, ale tento příběh si už budeme vyprávět někdy jindy.
34-4-3 Korelace nejsou tranzitivní (Zadání)
Úlohu řešme pomocí teorie grafů – veličiny budou vrcholy a studie hrany mezi nimi. Abychom však měli situaci jednodušší, pro každou veličinu si pořídíme vrcholy dva – jeden pro původní veličinu a jeden pro její negaci (například pro veličinu „být vysoký“ bychom měli vrcholy „být vysoký“ a „být nízký“). Hrana povede mezi vrcholy, pokud dané veličiny jsou podle nějaké studie kladně korelované. Tedy například, pokud existuje studie „čím více mléka lidé pijí, tím jsou vyšší“, pak povedeme hranu mezi vrcholy „být nízký“ a „nepít mléko“ a mezi „být vysoký“ a „pít mléko“.
Všimněme si, že v takovémto grafu odpovídá protipříklad pro Ondru cestě mezi veličinou a její negací. To proto, že hrany odpovídají jednotlivým studiím v kýžené posloupnosti studií. My potřebujeme takovou cestu nalézt.
Nejprve potřebujeme nalézt nějakou veličinu, ze které taková cesta vede. To můžeme udělat tak, že si pomocí prohledávání do hloubky (nebo do šírky či čehokoliv jiného) najdeme komponenty souvislosti grafu. Nyní nás zajímá, zda existuje nějaká veličina, že její negace je ve stejné komponentě jako ona. To můžeme udělat například tak, že si komponenty předtím očíslujeme, a porovnáváme čísla komponent, do kterých bod patří.
Jakmile takovou veličinu máme, musíme ještě zkonstruovat cestu mezi veličinou a její negací, což opět můžeme udělat například prohledáváním do hloubky.
Rozklad na komponenty souvislosti zvládneme v lineárním čase, kontrola pro každou veličinu je konstantní, takže celkově také lineární. I druhé prohledávání je lineární, celková časová složitost je tak lineární vzhledem k velikosti nového grafu. Zároveň je lineární i vzhledem k velikosti grafu na vstupu, protože jsme počet hran a vrcholů pouze zdvojnásobili. Paměťová složitost je rovněž lineární.
34-4-4 Geometrie (Zadání)
Zamysleme se nad tím, co se stane, když dort někde rozřízneme přímkou. Nejprve chvíli předpokládejme, že přímka zatím neprochází žádným z vrcholů N-úhelníku. Tedy přímka prostupně prochází hranami, kterými se dostává dovnitř a ven z dortu. Nahlédneme, že za každou takovou oblast, kterou řez navštíví, se počet částí dortu o jedna zvýší. Jelikož na začátku se dort skládal z jedné části, po řezu, který navštívil dort K-krát, bude K+1 částí dortu.
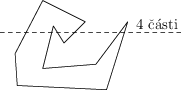
Co se bude dít o okolí vrcholů? V případě, že z vrcholu odchází hrany dortu na opačné strany řezu, tak je jedno, jakou z těchto stran dortu řez prochází. Složitější situace ovšem nastává v momentě, když obě hrany dortu směřuji na jednu stranu od řezu. Například nahoru. Kdybychom dort rozřízli pod vrcholem, tak počet částí bude o jedna menší než rozříznutí nad ním, protože řez potká o dvě hrany méně. Když povedeme řez přesně daným vrcholem, tak bude počet částí stejný jako v jednom z případů řezu posunutého o kousek na nějakou stranu. Záleží na tom, jestli se jedná o konvexní nebo nekonvexní úhel dortu. To naštěstí ale nebudeme muset řešit.
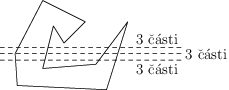
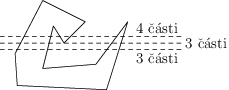
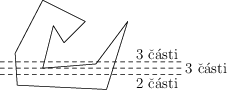
Speciální případ nastane, když jedna z odchozích hran je rovnoběžná s řezem. V ten moment můžeme dvojici vrcholů propojených touto hranou považovat za jeden vrchol a použít předchozí myšlenky.
Jednodušší varianta
Nyní se podíváme na jednodušší variantu. Tedy budeme hledat jen ty řezy dortu, kde nůž je rovnoběžný s osou x. Na tento případ se nám bude hodit technika zvaná zametání roviny přímkou. To si můžeme představit tak, že nad dortem budeme pohybovat nožem z jedné strany na druhou a budeme se dívat, na kolik částí by se aktuálně rozpadl. Nakonec odpovíme maximem z tohoto počtu.
To zní poměrně jednoduše a kdyby člověk řešil úlohu se skutečným dortem bez pomoci počítače, tak by to nejspíše dělal přesně takto. Jenže jak v počítači simulovat spojitý pohyb nože?
Všimneme si, že zajímavé věci se dějí jen v momentě, když nožem přecházíme pres nějaký vrchol N-úhelníku. Jindy se totiž počet částí nemůže změnit. Tedy části mezi vrcholy může náš program prostě přeskočit a stačí vždy spočítat počet částí dortu po řezu, který vedeme v blízkosti vrcholu.
Ovšem každý výpočet počtu částí nemusíme začínat od znovu. Můžeme postupovat odshora dolů a vždy využít předcházejícího výsledku. Stačí udělat pouze malou úpravu pro každý vrchol na dané souřadnici. Když vrchol má hrany na různé strany řezu, tak už jsme nahlédli, že se počet nijak nezmění. Když hrany z vrcholu vychází směrem, odkud s řezem přicházíme, tak se počet částí při průchodu bodem o jedna sníží. V opačném případě se o jedna zvýší. Zadání slibuje, že žádné dva body nemají stejnou y-ovou souřadnici, takže se nemusíme bát, že by maximum nastávalo jen v nějaké y-ové souřadnici a už ne v okolí alespoň na jednu stranu.
Celý algoritmus tedy bude probíhat následovně. Projdeme seznam bodů N-úhelníku a pro každý z nich zjistíme, který z případů změny počtů částí u něj nastane (stačí se podívat na y-ové souřadnice okolních bodů. Následně vrcholy seřadíme podle y-ové souřadnice. Posloupnost pak jen projdeme a budeme si počítat aktuální počet částí dortu. Odpovíme maximem z nich. To lze chápat také jako maximum z prefixových součtů změn hodnot.
Lehčí variantu tedy umíme řešit v čase O(N log N) s paměťovou složitostí O(N).
Zobecnění na kompletní úlohu
V obecné verzi potřebujeme uvážiti řezy, které nejsou rovnoběžné s osou x. Zase můžeme začít se spojitou simulací. Budeme dort otáčet a pro každé otočení si pomocí předchozího algoritmu spočítáme maximální počet částí, na které se rozpadne, když řez povedeme vodorovně s aktuálním natočením dortu.
Nyní se zbavíme spojité simulace. Všimneme si, že výsledek předešlého algoritmu se změní jen, když se prohodí pozice vrcholů v setříděném seznamu nebo se změní, jakým směrem vůči řezu směřují hrany kolem vrcholu. Obojí ovšem může nastat jen v momentě, když simulace projde stavem, kdy dva body mají stejnou y-ovou souřadnici. Můžeme tedy uvážit všechny spojnice dvojic vrcholů a simulaci zastavit jen v momentě, kdy nějaká z nich bude rovnoběžná s osou x. Pro každou takovou provedeme výpočet v natočení, kdy je spojnice rovnoběžná s řezem, a těsně poté.
Nakonec ještě poznamenejme, že díky tomu, že žádné tři body neleží na stejné přímce, nemusíme uvažovat natočení, kde nějaká spojnice je vodorovná. Můžete si rozmyslet, že mírným pootočením na jednu nebo na druhou stranu se situace nezhorší. Díky tomu zejména odpadne složitý případ, kdy dva body mají stejnou y-ovou souřadnici.
Když pro každou z O(N2) spojnic bodů budeme volat algoritmus řešící předchozí lehčí variantu, získáme řešení se složitostí O(N3 log N).
Zrychlujeme
I pro obecný případ můžeme využít toho, že předchozí řešení jen nepatrně poupravíme. Spojnice bodů budeme procházet v pořadí dle jejich úhlu od vodorovného směru (tedy jako kdybychom dortem skutečně spojitě otáčeli). Všimneme si, že u každé spojnice se v setříděném seznamu vrcholů jen prohodí daná dvojice. Když mezi dvojicí vede hrana, změní se to, na jakou stranu vedou sousední hrany od vrcholu. Místo toho, abychom vrcholy znovu třídili, můžeme jen danou dvojici pouze prohodit a přepočítat u ní změny hodnot. Pokud nemáme trojici bodů na stejné přímce, máme zaručeno, že prohazujeme sousední body.
Bohužel i když jsme se zbavili opakovaného třídění, moc jsme si nepomohli. Algoritmus má složitost O(N3). Pokaždé musíme procházet celou setříděnou posloupnost a hledat, kde je nejlepší udělat řez. Nebo nemusíme?
Kromě setříděné posloupnosti se můžeme pokusit si udržovat i prefixové součty změn hodnot (tedy počet částí za každým rozříznutím). Jako celková odpověď pak bude největší číslo, které jsme do prefixových součtů za celý běh algoritmu zapsali. Dále si ukážeme, že prefixové součty se mění jen lokálně. Pro každou dvojici prohozených vrcholů bude stačit jen změnit součet prefixu po prvním z vrcholů.
V případě, že se nezmění změny hodnot u vrcholů, tak je situace jednoduchá. Jelikož prohazujeme sousední vrcholy, všechny až na jeden prefixový součet obsahují buď oba, anebo žádný z vrcholů, a tedy se nezmění. Složitější situace nastane v momentě, kdy se změní změna hodnoty. To nastane pouze v případě, že prohazovaná dvojice je spojena hranou dortu. Rozborem případů, kam dort zatáčí v okolí vrcholů na následujícím obrázku, však zjistíme, že součet zůstane zachovaný, a tedy i tentokrát se prefixové součty obsahující oba dva vrcholy nezmění.
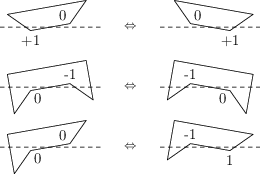
Tím jsme získali algoritmus, který spotřebuje O(N2 log N) času a O(N2) paměti. Nejnáročnější je setřídit spojnice bodů dle úhlu.
Trošku méně paměti
Na závěr si ještě ukážeme, jak zmenšit paměťové nároky programu.
Víme, že vždy prohazujeme sousední vrcholy, ovšem v setříděných posloupnostech hran máme naplánovaná všechna prohození již od začátku. Tedy i pro dvojice vrcholů, které jsou momentálně v posloupnosti daleko od sebe. Budeme si plánovat jen omezené množství budoucích událostí. Tedy jen prohození sousední dvojice vrcholů v posloupnosti, protože o ostatních víme, že zatím nemohou nastat. Místo setříděné posloupnosti budeme využívat haldu, abychom mohli za běhu události přidávat a případě odebírat. Když budeme prohazovat nějakou dvojici, smažeme prohození vrcholů dvojice se sousedem mimo dvojici a naplánujeme prohození dle aktuálního pořadí vrcholů.
Časová složitost zůstane stále O(N2 log N), ovšem paměťová se sníží na O(N).
34-4-S Manimujeme – 3D a grafy (Zadání)
K letošnímu seriálu nevydáváme řešení v klasické podobně, nicméně můžete se podívat na programy a animace od řešitelů: http://ksp.mff.cuni.cz/viz/34-5-S/komentare