Druhá série třicátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 36-2-1: Fronty na poště
- 36-2-2: Záchrana mravenců
- 36-2-3: Ztracená bunda
- 36-2-4: Nejlepší programovací jazyk, část II.
- 36-2-S: Chození po gradientu
 36-2-1 Fronty na poště (Zadání)
36-2-1 Fronty na poště (Zadání)
Pro začátek si všimněme, že chceme přijít na poštu těsně před tím, než přijde jiný zákazník. Kdyby tomu tak nebylo, tak jednoduše můžeme přijít o jednotku času později a zkrátit si tím čas čekání.
Co se stane, když přijdeme na poštu před zákazníkem i, oproti tomu, kdybychom na poštu nepřišli? Úředník ve frontě 0 místo původního zákazníka pošle do fronty nás. Zákazník za námi potom skončí ve stejné frontě jako původně zákazník za ním a tak dál. To, co se původně dělo zákazníkovi j (pro j ≥ i), se nyní děje zákazníkovi j+1, a my nahrazujeme zákazníka i.
A tedy všichni před zákazníkem i zůstávají nezměněni. Pozor, toto funguje jenom díky tomu, že zákazníci nebudou nikdy posláni zpět do fronty 0. Např. pro:
1 7
3 N
4 N
5 N
6 P
0 0
7 V
0
8 V
0
9 V
0
Pokud bychom přišli před prvním zákazníkem, tak by se nás vůbec nedostala řada.
To znamená, že když přijdeme před zákazníkem i, tak potom odejdeme v čase, kdy by býval odešel zákazník i, pokud bychom vůbec nepřišli.
Stačí si tedy odsimulovat celý proces na poště bez nás. Po jednotlivých frontách požadujeme, aby se dalo rychle přidat na konec a odebrat ze začátku, takže na to můžeme (překvapivě) použít frontu. Jednotlivé druhy událostí budeme obsluhovat následovně:
- Když přijde nový zákazník, tak ho dáme na konec fronty 0 a poznačíme si, v jakém čase přišel.
- Když je zákazník přesunut, tak ho z fronty j přemístíme do fronty k.
- A když zákazník odejde, tak ho z fronty odebereme a poznačíme si, v jakém čase odešel.
Na konci si spočítáme pro každého zákazníka s vyřízenou žádostí, kolik času na poště strávil, a přijdeme hned před ním. Na poště potom strávíme o tuto jednotku více času.
Simulaci i projití všech zákazníků stihneme v O(N) (kde N je počet událostí). Paměťová složitost bude také O(N).
 36-2-2 Záchrana mravenců (Zadání)
36-2-2 Záchrana mravenců (Zadání)
Vyplatí se zachraňovat jen ty mravence, na které něco může dopadnout. Dále když na mravence dopadne jedna šiška, tak je jednodušší ho zachránit, než když na něj dopadnou dvě. Tedy budeme nejprve chtít zachraňovat ty mravence, na které dopadne nejméně šišek.
Jak to spočítat? Naivně můžeme pro každého mravence projít všechny šišky a podívat se, jestli na něj dopadnou. To je ale hodně pomalé, až O(N2S).
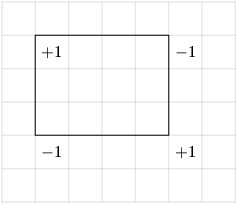
Můžeme to vylepšit tak, že použijeme (inverzní) dvourozměrné prefixové součty, ty sestavíme tak, aby nám říkaly, kolik šišek dopadne na každé políčko. V levém horním rohu šišky přičteme 1, v pravém horním rohu šišky 1 zase odečteme (protože tam šiška končí). Taktéž v levém dolním rohu odečteme 1. Jenže takto bychom jedničku pro políčka pod a za šiškou odečetli dvakrát, takže v pravém dolním rohu zase 1 přičteme.
Takto nejprve do prefixových součtů započítáme všechny šišky a posléze z nich vypočítáme, kolik šišek dopadne na každé políčko. Celkem to stihneme v čase O(N2 + S).
Nyní, když známe, kolik šišek dopadne na každé políčko, umíme si najít všechna políčka, na která dopadne určitý počet šišek (přihrádkovým řazením). Nejprve budeme krabičky přiřazovat všem mravencům, na které dopadne jedna šiška, pak všem, na které dopadnou dvě a tak dále. Těchto přiřazovacích kroků může být nejvýše K. Také si můžeme všimnout, že přiřazovacích kroků nemůže být víc než N2, protože to bychom už zcela jistě zachránili všechny mravence.
Takže celkově nám algoritmus běží v čase O(N2 + S).
 36-2-3 Ztracená bunda (Zadání)
36-2-3 Ztracená bunda (Zadání)
Značka kuchařkové úlohy napovídá, že můžeme úlohu vyřešit pomocí Dijkstrova algoritmu. Ale jak?
Dijkstrův algoritmus se často představuje v kontextu plánovačů cest. Vrcholy pak představují křižovatky a body zájmu a hrany cesty mezi nimi. Dijkstrův algoritmus však můžeme využít i k řešení obecnějších problémů, které s hledáním nejkratší cesty na první pohled nijak nesouvisí. Stačí, abychom měli nějakou konečnou množinu stavů a různě drahých způsobů, jak mezi nimi přecházet. Poté můžeme pomocí Dijkstrova algoritmu najít způsob, jak se co nejlevněji dostat z jednoho stavu do druhého.
Prvním krokem tedy bude reprezentovat jízdní řády pomocí grafu.
Stav cestujícího se skládá ze dvou hodnot, a to zastávky a času (0:00 – 23:59). Vrcholy tedy budou reprezentovat právě dvojice zastávek a časů. Nemusíme však vytvářet vrcholy pro všechny možné dvojice, stačí ty, kde a kdy se děje něco zajímavého, neboli příjezd nebo odjezd vlaku. Také přidáme vrchol pro čas a místo začátku cesty.
Dále přidáme hranu pro každou akci, kterou může cestující provést. Akce jsou dvou druhů:
- jízda vlakem na další zastávku,
- čekání do dalšího zajímavého času.
Pro každý úsek každého vlaku tedy přidáme hranu vedoucí ze zastávky a času odjezdu do zastávky a času příjezdu. Při cestě vlakem není třeba mrznout na nástupišti, proto bude mít tato hrana nulovou cenu. Dále vrcholy v rámci jedné zastávky pospojujeme do kruhu podle jejich časů. Každé z těchto hran přiřadíme cenu odpovídající rozdílu časů, které spojuje.
Uvažujme například tento jízdní řád:
| R547: | Brno | 10:00, | Jihlava | 11:30, | Praha | 13:00 |
| EC243: | Jihlava | 10:00, | Brno | 11:30 | ||
| Ex75: | Praha | 10:45, | Jihlava | 12:30, | Brno | 13:45 |
Jeho graf bude vypadat takto:
Pokud se o vlaky zajímáte, tak vám možná tento graf připomíná grafikon.
Ke každé „vlakové“ hraně si také poznamenáme, jaký je její vlak a cílová stanice, abychom později mohli snadno nalezenou cestu vypsat.
Poté stačí použít Dijkstrův algoritmus, abychom našli nejkratší cestu z počátečního vrcholu do všech ostatních vrcholů. Jirka může dorazit domů v libovolný čas, takže poté projdeme všechny vrcholy v cílové stanici a vybereme z nich ten s nejnižší vzdáleností. Dijkstrův algoritmus nám také ke každému vrcholu určí seznam hran, po kterých se do něj dostaneme co nejkratší cestou. Projdeme tedy nejkratší cestu do zvoleného cílového vrcholu a vypíšeme informace o všech vlakových hranách, které potkáme.
 36-2-4 Nejlepší programovací jazyk, část II. (Zadání)
36-2-4 Nejlepší programovací jazyk, část II. (Zadání)
Úkol 1 – Nula [3b]
Jak jste si mohli při pročtení seznamu instrukcí všimnout, většina z nich
konzumuje číslo, které je na vrcholu zásobníku. Takové instrukce samozřejmě na
začátku použít nemůžeme, jinak bychom neuměli zrekonstruovat původní zásobník.
Nedestruktivních instrukcí máme pomálu: control flow instrukce, u kterých zde
nejde garantovat, že budou skákat na rozumné místo v programu, a pak ciferný
součet CS a medián
m. Medián vyžaduje pěkné
číslo navrchu, takže nám vlastně zbývá jenom CS.
Jaký může být výsledek CS pro 64-bitová znaménková čísla?
Číslo s největším ciferným součtem, které se do jejich rozsahu ještě vejde, je
8 999 999 999 999 999 999 (a jeho záporná verze) s ciferným součtem 170.
Pomocí CS tedy můžeme vyrobit jedno číslo, o kterém alespoň víme, že je z
rozsahu 0–170. Podívejme se, co se stane, když CS budeme ještě opakovat.
Jednoduchým programem či chytrým přemýšlením lze ověřit, že ciferný součet pro
170 a nižší čísla nikdy nepřesáhne 18, což je ciferný součet čísla 99.
Pojďme si rovnou ukázat dva způsoby, jak odsud postupovat.
První postup pokračuje s dalšími CS. Třetím opakováním CS totiž umíme získat
číslo z rozsahu 0–9. Dalšími opakováními už akorát vyrobíme kopii toho samého
čísla. Když máme za sebou dvě kopie stejného čísla, tak z nich už lze vyrobit
nulu.
Jeden nástroj, který se pro to nabízí, je instrukce
%,
popřípadě ekvivalentní REM.
Ty ale nebudou fungovat pro případ, kdy naše číslo je nulou (což
nastane, když na vrcholu zásobníku byla nula), protože dělit nulou bohužel
nelze. Naštěstí to je řešitelný problém, stačí ve správný moment přičíst
jedničku pomocí ++ a tím získat číslo z rozsahu 1–10. Pak stačí přidat
další CS a jsme na pěkném rozsahu 1–9. Výsledné jednociferné číslo si můžeme zduplikovat pomocí
CS, a nyní už % či REM budou fungovat. Alternativně lze
použít instrukci funkcia, která taktéž pro dvě stejná čísla za sebou
vždy vyrobí nulu, a dokonce jí nula na vstupu nevadí. Nakonec už jen zbývá
odstranit mezivýsledky pomocí pop2.
Máme tedy následující dva programy na výrobu nuly:
CS CS CS ++ CS CS % pop2 pop2 pop2
CS CS CS CS funkcia pop2 pop2
Druhý, ještě kratší postup je využít instrukci lensum. Jakmile provedeme
CS CS, tak máme na vrchu zásobníku dvě čísla, která mají
maximálně délku 3 a 2 (zase lze ověřit experimentem či přemýšlením,
„nejhorší“ případ je 169 a 16). Provedením lensum tedy dostaneme
číslo z rozsahu 0–5. Opět můžeme incrementovat a použít modulo, nebo rovnou
použít instrukci funkcia:
CS CS lensum ++ CS %
CS CS lensum CS funkcia
Mimochodem, toto jsou nám nejkratší známá řešení (první na počet znaků, druhé na počet instrukcí). Pokud vymyslíte kratší, dejte nám prosím vědět.
Pro fajnšmekry ještě nabízíme následující program na výrobu nuly:
CS CS ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++
++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++
++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++
++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++ ++
++ ++ bitshift
Poznámka o konstantách
Pokud by to nebylo zřejmé, nyní také umíme vyrábět rozumně malé kladné konstanty,
a to vyrobením nuly a poté použitím správného počtu instrukce ++. Jak si
v rozumném čase vyrobit větší konstanty prozatím ponecháváme otevřené.
Pro lepší čitelnost budeme v tomto řešení tomuto stavebnímu bloku říkat
push(n), kde n je konstanta, kterou přidáváme.
Úkol 2 – Negace [2b]
Jeden přímočarý způsob na řešení tohoto úkolu je pořídit si číslo -1
a poté jej vynásobit s číslem na vrcholu zásobníku pomocí instrukce u.
Druhý, kratší způsob si ukážeme poté.
Číslo -1 si můžeme pořídit hned celou řadou způsobů, tak si pojďme dva ukázat:
- Za pomoci instrukce
bitshiftau. Výsledkem operace1 << 63je záporné číslo -263, nejmenší reprezentovatelná hodnota. Z libovolného záporného čísla už umíme vyrobit -1 pomocí univerzální aritmetické instrukceus parametrem 5, která vrátí její znaménko.push(1) push(63) bitshift push(5) u - Za pomocí instrukce
qeq. Kvadratická rovnice (x+1)(x+1) = 0, neboli x2+2x+1 = 0, má jedno řešení, a to právě -1.push(1) push(2) push(1) qeq
Teď, když umíme implementovat push(-1), tak pro dokončení negace stačí
využít násobení pomocí instrukce u:
push(-1) push(2) u
Kratší negace
Ještě jsme slíbili alternativní, kratší způsob. Instrukce qeq umí totiž
řešit i lineární rovnice, stačí nastavit koeficient a u x2 na nulu.
Pro libovolné číslo k na vrcholu zásobníku vyrobíme rovnici x + k = 0 a tu
vyřešíme pomocí qeq, výsledkem je totiž -k:
push(1) push(0) qeq
Nejkratší (na počet instrukcí) nám známé řešení, které oproti předchozímu akorát optimalizuje výrobu nuly:
CS CS lensum CS funkcia ++ CS CS % qeq
Podobně jako u předchozího úkolu nám prosím dejte vědět, pokud vymyslíte ještě kratší řešení na počet instrukcí.
Poznámka o psaní ksplangu
Jak jste si jistě všimli, postupně získáváme nové stavební bloky, které se hodí pro psaní složitějších programů. Mohli bychom je vkládat do ksplangových programů v textovém souboru ručně, ale mnohem rozumnější a pohodlnější přístup je vytvořit si nějaký nástroj, který ksplang generuje.
Takovým nástrojem může být například preprocessor, který umí na vstupu přečíst ksplang s novými instrukcemi a vygeneruje reálný ksplangový program. Další a výrazně snazší alternativou je program, který ksplang generuje přímo, a místo psaní ksplangu voláme funkce v jiném jazyku, který nám ten ksplangový program vygeneruje.
Zejména budeme od takového nástroje chtít, aby uměl na zásobník přidat všechny konstanty, co potřebujeme (doporučujeme umět vyrobit každou konstantu). Také může být pohodlné umět snadno používat instrukce s konstantními parametry.
Úkol 3 – Duplikace [5b]
V tomto úkolu bylo cílem zduplikovat na zásobníku číslo k, abychom získali
velice užitečný stavební prvek, kterému budeme říkat dup.
Rovnou prozradíme, že lze napsat duplikaci, která umí zpracovat libovolné
číslo, a na konci řešení ji naleznete, byť bez detailního vysvětlení.
Detailněji si popíšeme pouze varianty, které umí omezenější rozsah hodnot.
Nastal čas vyzkoušet si druhou z nedestruktivních instrukcí, a to medián
m.
Nabízí se hned několik možností, jak ho použít, a víceméně každá z
nich vyžaduje nějaké obcházení speciálních případů. Hlavní rozhodnutí, co
nás čeká, je počet prvků, přes které budeme medián počítat. Instrukce m nám
přišla s popisem „vrať medián z horních x čísel, kde x je číslo na vrchu
zásobníku“, což samozřejmě znamená, že se číslo x neodstraňuje, a medián se
počítá i z něj.
Medián dvou čísel
První možností je použít medián dvou čísel, což znamená, že po použití m
máme na zásobníku hodnotu, která vychází (k+2)/2, zaokrouhlená směrem k nule.
Bohužel právě tento způsob zaokrouhlování přináší potíže: podívejte se v
následující tabulce na čísla -1, -2, nebo -3, kde se to chová
zvláštně:
| vstupní k | výsledek m |
| -7 | -2 |
| -6 | -2 |
| -5 | -1 |
| -4 | -1 |
| -3 | 0 |
| -2 | 0 |
| -1 | 0 |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 2 |
Pokud si ale před použitím instrukce m číslo k vynásobíme dvěma, tak
se najednou vše začne chovat mnohem rozumněji. Můžeme to provést třeba sekvencí
push(1) bitshift.
Ještě je potřeba si uvědomit, že jsme si tím snížili rozsah duplikovatelných
čísel na -262 až 262-1.
S tímto trikem už není těžké domyslet, jak duplikaci dodělat. V následujícím programu v komentářích ukazujeme hodnoty, které jsou zrovna na konci zásobníku mezi sekvencemi instrukcí:
# k
push(1) bitshift
# 2k
push(2)
# 2k 2
m
# 2k 2 k+1
push(-1) push(0) u
# 2k 2 k
push(1) push(3) lroll
# k 2k 2
push(1) push(2) lroll
# k 2 2k
push(3) u
# k k
Alternativně bychom mohli místo dvou použití lroll použít pouze
jeden lroll na prohození horních dvou čísel, znovu opakovat operaci m, a na
konec odečíst jedničku.
Medián tří čísel
Jinou možností je použít medián 3 hodnot, kde žádné problémy se zaokrouhlováním nejsou. Najednou ale máme problém, že nelze vybrat žádnou třetí hodnotu a, která by zaručila, že mediánem trojice 3, k, a je číslo k. Pro k < 3 a k > 3 bychom potřebovali různá a.
Naštěstí existuje jednoduchý trik, pokud nám stačí podporovat duplikaci čísel z
omezeného rozsahu, jako například 32-bitová čísla, což pro vyřešení úkolu
stačilo. Můžeme totiž k číslu k nejdříve přičíst offset – v našem
případě číslo větší než 232+3, aby nejmenší možná hodnota k byla také 3
nebo větší. Poté můžeme použít medián 3 čísel s třetí hodnotou a >
232+offset. Nakonec offset odečteme od výsledku m i od duplikovaného
čísla. Samozřejmě nesmíme zapomenout odstranit trojku a a, které po mediánu
zůstaly.
V následujícím kódu volíme pro jednoduchost offset 233 a třetí hodnotu a
= 262. Implementovat push(2^c) můžeme pomocí push(1) push(c) bitshift.
Znegovat takové číslo pak umíme z předchozího úkolu.
push(2^33) push(0) u # přičteme offset
push(2^62) push(3) m # přidáme a, 3, provedeme medián
pop2 pop2 # odstraníme 3, a
push(-2^33) push(0) u # odečteme offset od výsledku mediánu
push(1) push(2) lroll # prohodíme horní 2 prvky
push(-2^33) push(0) u # odečteme offset od původního čísla
Univerzální duplikace
Následující duplikace umí zduplikovat všechna čísla.
CS CS lensum ++ CS lensum m CS CS lensum CS funkcia CS ++ CS qeq u CS CS
lensum CS funkcia ++ bitshift CS CS lensum ++ CS lensum m CS CS lensum CS
funkcia CS ++ CS qeq u CS CS lensum CS funkcia ++ bitshift pop2 CS CS
lensum ++ CS lensum CS ++ ++ lroll m CS CS lensum CS funkcia ++ CS CS
funkcia qeq CS CS lensum CS funkcia ++ bitshift pop2 CS CS lensum CS
funkcia u ++ ++ ++ CS CS CS CS lensum CS funkcia CS ++ CS qeq u CS ++ CS
lensum CS ++ ++ lroll CS funkcia u CS CS lensum CS funkcia ++ CS ++ ++
lroll CS CS lensum CS funkcia CS ++ CS qeq u CS CS funkcia u
 36-2-S Chození po gradientu (Zadání)
36-2-S Chození po gradientu (Zadání)
Úkol 1 – Minibatch SGD s regularizací [9b]
První úkol byl o implementaci SGD.
U ukázkové implementace jsme použili většinou čistý Python,
jen na odečítání vektorů jsme použili knihovnu numpy,
protože chceme ukázat, že numpy dokáže velmi
zkrátit a zpřehlednit kód (a jako bonus i zrychlit).
Pro přehlednost jsme do komentáře napsali i kód bez použití numpy.
Úkol 2 – Feature engineering [3b]
Úkol měl za cíl vás seznámit s vytvářením featur pomocí předpřipravených
transformerů dat v knihovně scikit-learn.
Také jsme celkem čekali, že tento kus kódu poté zkopírujete do soutěže a pomůže
vám projít přes práh.
Úkol 3 – Soutěž [3b]
Soutěž měla spoustu možných řešení, náš přístup byl přes vytváření nových featur a ne moc o vybírání typu modelu nebo o spouštění spousty testů na vyladění hyperparametrů modelu.
Pro naše testy jsme používali model RidgeCV, kde jsme zkoušeli
různé hodnoty alpha od 10-3 do 104. Pro zajímavost budeme
ze začátku uvádět i model LinearRegression, který nemá žádnou regularizaci.
Pro začátek zkusíme předhodit všechny featury z datasetu do modelu (bez žádných úprav) a uvidíme, co naučený model dokáže. Vždy budeme uvádět trénovací i testovací chybu (byť samozřejmě během soutěže testovací chybu neznáme, tedy všechna rozhodnutí se vždy dělají podle trénovací chyby). Chyba je vždy RMSE počítaná buď na celém trénovacím či testovacím datasetu.
| Model | Trénovací chyba | Testovací chyba |
| LinearRegression | 429.592 | 438.156 |
| RidgeCV | 429.594 | 438.119 |
Vidíme, že modely se chovají velmi podobně, což je celkem zajímavé. Dále vidíme dobrou korelaci mezi testovacími a trénovacími daty.
Nyní zkusme přidat StandardScaler na všechny featury, kde to dává
smysl, tedy na sloupce 2 až 9.
| Model | Trénovací chyba | Testovací chyba |
| LinearRegression | 429.592 | 438.156 |
| RidgeCV | 429.595 | 438.113 |
Pro LinearRegression se nic nezměnilo, protože tento model si jen přeškáluje váhy
a tím pádem se chová stejně. Pro RidgeCV se chyba trochu zlepšila.
Tato transformace zatím moc nepomohla. Zkusme nyní použít jen OneHotEncoder
na ty sloupce, které jsme neměnili v minulém pokusu.
| Model | Trénovací chyba | Testovací chyba |
| LinearRegression | 352.131 | 357.830 |
| RidgeCV | 352.131 | 357.833 |
One hot encoding nám pomohl o mnoho lépe. Může se zdát zbytečné používat one hot encoding na binární featury, ale ve skutečnosti je to velice dobrý nápad, protože pro stav ano a ne může mít model různé váhy, což by pomocí jedné featury 0/1 nebylo možné.
Nebudeme zde uvádět kombinaci StandardScaleru a OneHotEncoderu,
protože rozdíl je minimální.
Zkusíme k OneHotEncoderu přidat polynomiální featury do 2. stupně,
což je jeden způsob, jak zesílit sílu našich lineárních modelů.
| Model | Trénovací chyba | Testovací chyba |
| LinearRegression | 313.116 | 321.109 |
| RidgeCV | 39557937747.911 | 39771133464.195 |
Pro lineární regresi to pomohlo a dokonce bychom se už dostali do soutěže,
ale pro RidgeCV to byla katastrofa. Důvod je celkem jednoduchý,
v datasetu máme celkem velké množství featur, které dosahují řádu 103, tedy
po přidání polynomiálních featur se můžeme dostat až na řád 106.
Lineární modely moc velké featury dokáží snížit pomocí váhy a to může fungovat,
ale pokud se obrovské váhy snažíme regularizovat, tak můžeme narazit na tento
problém. Když použijeme před polynomiálním transformací
ještě transformaci StandardScaler, tak se chování modelu
RidgeCV zlepší a dokonce dosahuje lepších výsledků než model bez regularizace,
kde se už objevuje celkem overfitting.
| Model | Trénovací chyba | Testovací chyba |
| LinearRegression | 158.236 | 413.048 |
| RidgeCV | 190.795 | 311.475 |
Vyrábění nových featur
Základní úkol jsme splnili, nyní zkusme být co možná nejlepší v soutěži.
Pro začátek můžeme začít s pozorováním, že učit model na datech, kde systém
nefungoval, nedává moc smysl, protože hodnota je vždy nula.
Tedy zahodíme data, kde tento stav nastal, a můžeme v ColumnTransformeru
zahodit sloupec s danou featurou. Když děláme predikci, tak musíme udělat
dodatečnou korekci predikcí. Když nastalo, že systém nefungoval, tak predikce
bude nula.
Když toto naimplementuje, tak se chybová funkce o něco zlepší. Train: 191.158,
test: 310.891 (dále budeme uvádět už jen model RidgeCV).
Druhé celkem snadné pozorování je, že nedává smysl predikovat záporné hodnoty, protože půjčit si -2 kola nedává moc smysl. Když přidáme tuto změnu, tak se chyba zase o něco sníží. Train: 190.238, test: 305.435.
Dobrá, toto byla malá zlepšení, ale snížení o pár bodů RMSE je lepší než nic. Nyní se podívejme na featury z datasetu. Můžeme si všimnout, že známe datum, které nemusí modelu hodně pomoci. Z dat nepoznáme, jestli je víkend, nebo že v nějakém dni v týdnu máme náhlý pokles či nárůst poptávky. Můžeme tedy zkusit přidat featuru, která bude říkat den v týdnu. Train: 145.509, test: 257.608.
Dále můžeme přidat „klasifikaci“ dne. Rozdělíme si den na 4 segmenty.
Jelikož data jsou z Jižní Koreje, což nebylo v zadání, a také se mi nechtělo
přemýšlet, jaká časová zóna je v datech, tak jsem den rozdělil po 6 hodinách.
Pro implementaci jsem si napsal vlastní transformaci, ale jednodušší
řešení by bylo použít KBinsDiscretizer, který je popsán později.
Train: 139.993, test: 266.174. Zde máme zhoršení na testovacích datech, ale
zlepšení na trénovacích. Jelikož testovací chybu nevidíme a rozhodujeme se
podle trénovací chyby, tak toto je pro nás „zlepšení“.
Dále zkusíme přidat klasifikaci síly větru podle Beaufortovy stupnice. Model si nemusí úplně uvědomit podle čísla (a ještě k tomu přeškálované), že daná síla větru je silná (v monzunu asi málo lidí bude jezdit na kole). Train: 136.547, test: 282.418. Zde opět vidíme zhoršení na testovací chybě.
Poslední featurou, kterou přidáme, je klasifikace viditelnosti. Jelikož u viditelnosti není pevná škála, tak jsem si jednu vybral a použil. Train: 136.232, test: 283.521. Zde je trochu sporadické, jestli se vyplatí přidávat tuto feauturu. Pokud bychom ale všechny předešlé testy zopakovali s polynomiálními featurami do stupně 3, tak zlepšení na trénovacích datech je už přes 1 RMSE.
Finální natrénovaný model s polynomiálními featurami do stupně 3 má chybu na trénovacích datech 89.302 a 183.864 na testovacích.
Nestabilní výsledky RidgeCV
V průběhu řešení úkolu jste mohli narazit na podivnou věc.
Máte obstojně fungující model na datech, poté přidáte novou featuru a najednou
RMSE vyletí. Když se pokusíte naučit model znovu na jiném počítači,
tak se tento jev vůbec neobjeví. Co se děje? S největší pravděpodobností
je to způsobeno tím, že model RidgeCV je náchylný na numerickou
stabilitu. Jelikož RidgeCV vypočítává váhy explicitně a matematickými triky
se zajistí, že model neuvidí jedno dato pro udělání cross validace. Proto jakákoliv
malá chyba může způsobit velké změny výsledků.
Jiné modely, jako například SGD, jsou velice stabilní, ale za cenu toho, že cross validace
bude trvat déle.
SplineTransformer
Dalšího možného vylepšení můžeme docílit použitím dalších transformací, jako například
SplineTransformer (někteří dokonce použili při řešení této soutěže). Tato
transformace udělá to, že pro každou featuru vrátí vektor hodnot, který reprezentuje
danou hodnotu featury pomocí b-splines.
B-spline (basis spline) je křivka, která je namodelovaná pomocí pomocí n+1 řídicích bodů P0, P1, …, Pn a stejného počtu polynomiálních funkcí (basis functions). Každý řídicí bod má svou bazickou funkci d-tého stupně. Samotný tvar bazických funkcí závisí jen na bodech nazývající se uzly (knots) a zcela nezávisí na hodnotách řídicích bodů (jsou to plně oddělené věci). Těchto uzlů je n+d+2. Tento počet se odvíjí od toho, že d-tý stupeň bazické funkce je definován na d+1 po sobě jdoucích uzlů a těchto funkcí potřebujeme n+1.
Pokud to zní až moc abstraktně, tak nezoufejte, protože za chvíli vysvětlíme, jaká je motivace za touto transformací dat. Ale nejprve začněme zjednodušovat – nás nezajímá vykreslení křivky (chceme jen reprezentaci nějaké hodnoty pomocí bazických funkcí). Můžeme tedy zcela zapomenout na nějaké řídicí body, které slouží jen k vykreslení křivky.
Nastavení počtu uzlů, stupně funkcí d a způsob, jak se tyto uzly nastavují, jsou hyperparametry transformace. Můžeme je nastavit ručně nebo můžeme použít buď uniformní (všechny uzly jsou stejně vzdálené a první uzel se vezme jako nejmenší hodnota featury z dat a poslední jako největší hodnota featury z trénovacích dat), či nastavit kvantilově.
Dobrá, dost abstraktních věcí, pojďme se podívat, co to reálně dělá. Chceme reprezentovat den v týdnu pomocí b-spline. Vytvoříme si b-spline transformaci a naučíme ji na datech. Pro jednoduchost budeme mít jen 7 „dat“ a každé dato bude reprezentovat jeden den v týdnu.
import numpy as np
from sklearn.preprocessing \
import SplineTransformer
def periodic_spline_transformer(
period,
n_splines=None, degree=3):
if n_splines is None:
n_splines = period
n_knots = n_splines + 1
return SplineTransformer(
degree=degree,
n_knots=n_knots,
knots=np.linspace(0, period, n_knots)
.reshape(n_knots, 1),
extrapolation="periodic",
include_bias=True,
)
data = np.array(
[0, 1, 2, 3, 4, 5, 6]
).reshape(-1, 1)
transformer = periodic_spline_transformer(7)
splines = transformer.fit(data)
extrapolation="periodic" říká, jak se má chovat transformace mimo
naučený interval. V našem případě je v týdnu periodická featura
(hodnoty se po nějaké periodě opakují), hodí se tedy, aby křivka byla periodická.
Další možné extrapolace je například "constant", kde se hodnota
mimo naučený interval chová jako jeden z krajních uzlů.
Pro lepší pochopení transformace vykreslíme bazické funkce.
import matplotlib.pyplot as plt
x = np.linspace(0, 7, 1000).reshape(-1, 1)
y = transformer.transform(x)
plt.plot(x, y)
plt.legend([
f"bazická fce {i}"
for i in range(y.shape[1])
])
plt.xlabel("dny v týdnu")
plt.ylabel("hodnota bazických funkcí")
plt.show()
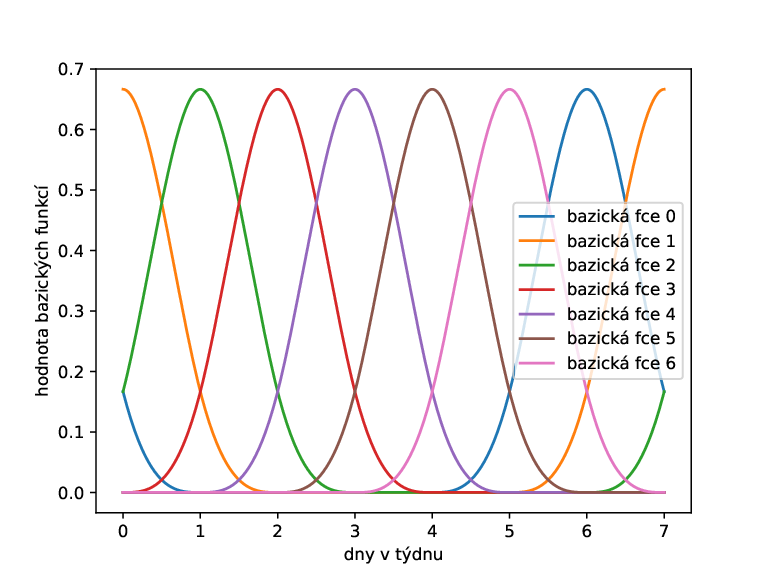
Z obrázku vidíme, že libovolný bod je reprezentován pomocí až 4 nenulových bazických hodnot (ostatní bazické hodnoty mají hodnotu 0). Toto není náhoda, protože každý uzel se účastní d+1 bazických funkcí (v našem případě d=3). Dokonce celá čísla jsou reprezentovaná pomocí 3 nenulových bazických hodnot. Navíc hodnoty bazických funkcí v celých číslech vypadají tak, že jedna funkční hodnota je větší a funkce předchozí a následující mají stejnou nebo menší hodnotu. To v praxi znamená, že do dat vkládáme určitou formu nejistoty. Zde to konkrétně znamená, že i když v datech máme řečeno, že daný den je čtvrtek, tak touto transformací říkáme, že na 66.6 % je to čtvrtek, ale na 16.6 % je to ve středu a v pátek. Že se tato čísla sčítají do jedničky není náhoda, protože tyto funkce jsou takto konstruované. Navíc jelikož b-spline je periodická, tak se transformace bude chovat dobře i okrajích intervalu. Dato v neděli bude mít hodnotu 16.6 % pro sobotu a pondělí.
Tuto transformaci dává spíše větší smysl použít na hodiny než na dny v týdnu, protože touto transformací můžete vložit do dat až velkou nejistotu.
Pokud se chcete dozvědět více o kreslení různých křivek, doporučuji toto video. Sice je delší, ale vše je v něm nádherně graficky vysvětleno.
Pokud se chcete více dozvědět o b-splinách, tak doporučuji tento web, kde jsou i interaktivní příklady. Můžete zde měnit řídicí body a uzly a zjišťovat, jaký dopad to má na tvar křivky či podobu bazických funkcí.
KBinsDiscretizer
Poslední transformaci, kterou zmíním, je KBinsDiscretizer.
Tato transformace je velice jednoduchá na vysvětlení: Vezme data featur a hodnoty
rozdělí do n intervalů. Poté první interval dostane hodnotu 0, druhý 1, atd.
Metod rozdělení máte několik. Buď uniformní, což nemusí být nejlepší volba
kvůli hodnotám daleko od ostatních, nebo kvantilově, kde se tyto hodnoty chovají lépe,
nebo algoritmus k-means, o kterém se budeme bavit v jednom budoucím díle seriálu.
Pokud máte libovolné otázky k řešení, tak se nebojte zeptat na našem Discordu. Jen prosíme, neposílejte žádné zdrojové kódy.