Třetí série třicátého šestého ročníku KSP
Celý leták v PDF.
Dostává se k vám třetí číslo hlavní kategorie 36. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: neděle 18. února 2024 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo nám napíše řešení 1 teoretické úlohy v angličtině. Pro inspiraci nabízíme anglické řešení části 3. série 35. ročníku. Kdybyste si nebyli jistí terminologií, napište nám na english@ksp.mff.cuni.cz, rádi poradíme.
Zadání úloh
- 36-3-1: Modla pro hroší bohy
- 36-3-2: Paměťově omezený tablet
- 36-3-3: Hromady odpadu
- 36-3-4: Nejlepší programovací jazyk, část III.
- 36-3-S: Učíme klasifikátory
- 36-3-S2: Soutěžní úloha seriálu
- 36-3-X1: Výlet do Japonska
 36-3-1 Modla pro hroší bohy (11 bodů)
36-3-1 Modla pro hroší bohy (11 bodů)
Obyvatelstvo Hrochova vždy žilo v míru a pokoji pod ochranou hroších bohů. Poslední dobou je ale začala sužovat častá zemětřesení. Jestli to takhle půjde dál, tak zanedlouho z města nic nezbude. Určitě museli své bohy něčím rozhněvat. Aby si je udobřili a zachránili město, rozhodli se vzít největší kámen, který vydolovali v místním lomu, a udělat z něj modlu pro hroší bohy. Aby minimalizovali šanci dalších zemětřesení, rozhodli se modlu postavit tak, aby byla co nejvyšší. Hroší bohové přece nebudou chtít třást zemí, když tím hrozí, že si povalí vlastní modlu.
Kámen má tvar konvexního mnohoúhelníku. Najděte, na kterou stranu se má postavit, aby byl nejvyšší. Modla bude podepřená, takže může stát na libovolné straně, bez ohledu na polohu těžiště. Pokud více stran dosáhne stejné výšky, můžete vybrat libovolnou.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku je číslo N – počet vrcholů mnohoúhelníku. Na každém z dalších N řádků jsou celočíselné souřadnice x a y jednotlivých vrcholů.
Formát výstupu: Na výstup vypište jedno číslo – index strany, na kterou se má mnohoúhelník postavit. Strany jsou indexované podle prvního vrcholu. Strana jedna vede mezi prvním a druhým, strana dva mezi druhým a třetím a tak dále, až nakonec hrana N vede mezi N-tým a prvním.
5 -1 2 -1 -1 2 -1 5 3 3 5
4
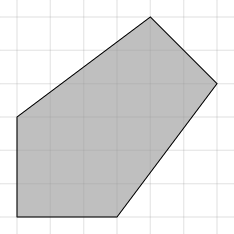
Na první a druhé straně má výšku 6, na třetí a páté 4,2 a na čtvrté 5√2. Nejvyšší je tedy na čtvrté.
 36-3-2 Paměťově omezený tablet (11 bodů)
36-3-2 Paměťově omezený tablet (11 bodů)
„Tablete, tablete, řekni mi, kdo je na světě nejsymetričtější?“ ptá se opět král. Tentokrát se ovšem neptá kouzelného zrcadla. Zrcadlo král vyhodil a pořídil si chytrý nástěnný tablet! Tablet vyfotí kamerami spoustu obrázků krále a vyhodnotí jeho symetričnost na svém procesoru. Nicméně výrobci šetřili, dali mu málo paměti, která sotva stačí na pár obrázků.
Tentokrát není problém v rozhodování symetričnosti krále, to tablet hravě zvládne. Ale aby to udělal, musí nejdříve pořízené obrázky předzpracovat – vlastně vyhodnotí něco jako matematický výraz, který s obrázky počítá: nejdříve „zprůměruje“ obrázek levého ucha krále s jeho nosem, poté „sečte“ obrázky levé a pravé nohy, výsledky spolu „vynásobí“, a tak dále…Výpočet na obrázcích se vlastně dá popsat binárním stromem.
Vstupem vašeho algoritmu bude binární strom, který popisuje vyhodnocování nějakého „matematického“ výrazu, který ale místo s čísly počítá s obrázky. Listy jsou obrázky krále, vnitřní vrcholy reprezentují operaci, která nějak kombinuje dva obrázky do jednoho či transformuje jediný obrázek (vrcholy s jen jedním synem jsou tedy povoleny, viz příklad níže), výsledek z kořene je pak finální obrázek, ze kterého tablet už snadno určí symetrii krále. Obrázky jsou ale velké, tudíž vaším úkolem je vymyslet, jak zadaný strom vyhodnotit v takovém pořadí, abyste si v průběhu museli pamatovat co nejméně obrázků. Máte tedy najít jakýsi plán výpočtu.
Všechny obrázky, tedy listy i výsledky vnitřních vrcholů, jsou stejně velké. Obrázky v listech jsou v počátku výpočtu uloženy na disku tabletu, paměť tedy spotřebují, až jakmile je chcete použít pro vyhodnocení nějaké operace. Pro vyhodnocení typického vnitřního vrcholu se dvěma potomky je vždy potřeba použít minimálně tři kusy paměti zároveň: dva, ve kterých už jsou uloženy obrázky obou potomků vyhodnocovaného vrcholu (ať už jsou vnitřním vrcholem nebo listem), a jeden, kam se uloží výsledek.
Struktura stromu je dána pevně a není možné ji měnit. Například nelze využívat případné komutativity nebo asociativity operací ve vrcholech – o operacích ostatně vůbec nic nevíme.
Vymyslete algoritmus, jak pro libovolný binární strom určit pořadí vyhodnocování vrcholů, při kterém se spotřebuje přesně optimální množství paměti. Pozor, že nám nestačí asymptoticky optimální paměť, chceme jí opravdu spotřebovat co nejméně v absolutních číslech: plán, který na nějaký strom spotřebuje paměť na 10 obrázků, je horší než plán, který musí ukládat jen 9 obrázků. Tedy počet zapamatovaných obrázků v paměťově nejnáročnějším místě vámi naplánovaného výpočtu musí být co nejnižší. Paměť měříme pouze na počet obrázků.
Naopak váš algoritmus, který bude plán hledat, nemá žádná časová nebo paměťová omezení. Jeho časová složitost by ale měla být, tentokrát asymptoticky, co nejrychlejší.
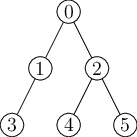
V příkladu výše by plán výpočtu, který počítá vnitřní vrcholy (či načítá listy) v pořadí 3, 1, 4, 5, 2, 0,
použil v nejnáročnějším místě výpočtu paměť na 4 obrázky, a to při počítání vrcholu číslo 2,
protože je potřeba si pamatovat výsledek z vrcholu 3, listy 4 a 5 a navíc i místo na výsledek pro vrchol 2.
Plán 4, 5, 2, 3, 1, 0 je ovšem lepší, a v tomto případě i optimální. V nejnáročnějším místě
si totiž pamatuje jen 3 obrázky. Toto nastane hned několikrát, konkrétně při počítání vrcholů 2, 1 a také 0.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-3-3 Hromady odpadu (12 bodů)
36-3-3 Hromady odpadu (12 bodů)
Vánoce a Silvestr skončily a zanechaly za sebou spoustu nepořádku. Kevin se proto rozhodl, že by si rád letos u sebe doma pořádně uklidil. Nebude to však mít jednoduché, tuto činnost během minulého roku značně zanedbával a v pokoji mu mezitím vyrostlo N hromad odpadu. Každá taková hromada má nějakou výšku vi a odpovídá sloupci na sobě naházených vi předmětů.

Protože Kevin rád pracuje efektivně, přinesl si k usnadnění úklidu pracovní nářadí – lopatu a velmi silnou kyselinu.
Lopatou je schopen vždy nabrat libovolný počet předmětů z vrchu jedné z hromad a vyložit je kousek vedle. Tím danou hromadu sníží o nějaké celočíselné k a zároveň založí novou hromadu výšky k. Kevinův pokoj je neobvykle prostorný, takže takto může v průběhu úklidu založit libovolný počet hromad celočíselné výšky.
Pokud Kevin nechce odpad jen přemístit, ale přímo zničit, použije kyselinu. Tu je schopen jedním pohybem rovnoměrně rozprostřít po všech hromadách a nechat ji na každé hromadě rozleptat jeden předmět z vrchu.
Vaším úkolem bude vytvořit algoritmus, jež pro Kevina nalezne nejkratší možnou posloupnost těchto dvou operací, tedy rozdělení jedné hromady na dvě celé části a snížení všech hromad o 1, vedoucí k odstranění veškeré nečistoty.
Můžete předpokládat, že jsou hromady poměrně nízké. Tím myslíme, že výška nejvyšší z hromad bude řádově tak velká jako celkový počet hromad N.
Pokud má například Kevin v pokoji hromady výšek 5, 7, 13, tak je jeden z možných postupů použít kyselinu a snížit všechny hromady o 1. Tím získáme hromady výšek 4, 6, 12. Následně v jednom kroku rozdělíme hromadu výšky 12 na dvě hromady výšky 6. Zbyly nám tak hromady výšek 4, 6, 6, 6, kterých se jednoduše zbavíme použitím kyseliny šestkrát za sebou. K úklidu jsme celkem potřebovali 8 kroků a lze ukázat, že rychleji to nejde.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-3-4 Nejlepší programovací jazyk, část III. (11 bodů)
36-3-4 Nejlepší programovací jazyk, část III. (11 bodů)
V předchozí části jsme se naučili vyrábět konstanty a duplikovat čísla. Tentokrát je čas v ksplangu – našem nejlepším programovacím jazyku – konečně napsat nějaké pořádnější programy.
Pokud jste ne(vy)řešili předchozí část, vůbec to nevadí. Nahlédněte do řešení předchozí části, kde najdete potřebné stavební bloky (vyrobení nuly, záporných čísel, univerzální duplikaci), které můžete v této části vkládat do svých programů.
Do řešení předchozí části se podívejte i v případě, že jste předchozí úlohu vyřešili. Naleznete v něm totiž duplikaci, která je univerzální, tedy zvládne zduplikovat libovolné číslo. V předchozí úloze stačilo naprogramovat duplikaci pro omezený rozsah čísel, nicméně tentokrát se bude na řešení úkolů hodit právě tato univerzální varianta. Také je možné, že v řešení najdete nové užitečné triky.
Kromě toho jsme vylepšili náš simulátor, nyní je v něm možno program krokovat a podívat se na stav zásobníku po každé instrukci. Další novinkou je možnost zapnout textový režim, kdy do zásobníku můžete zapisovat text. Vstupní text se převede na Unicode code pointy a výstup programu se po doběhnutí také vypíše jako text. V této úloze textu ještě nevyužijeme, ale zlepšuje to možnost použití ksplangu v produkci.
Tuto úlohu odevzdávejte v odevzdávátku, podobně jako běžné opendata úlohy. Generované vstupy můžete v odevzdávátku ignorovat, vaše ksplangové programy odevzdávejte v textové podobě jakožto výstup k danému úkolu. Po odevzdání je náš interpreter ksplangu spustí na několika neveřejných testovacích vstupech a dá vám vědět o výsledku.
Zásobník má omezený počet prvků, v této úloze je to vždy 2 097 152, a jeho překročení ukončí program chybou. Ve všech úkolech můžete předpokládat, že se na zásobník vejde aspoň dalších 1000 čísel. Narozdíl od předchozí úlohy můžete při velmi neefektivní implementaci narazit na časový limit. Nastavili jsme jej tak, že by vaše programy měly stíhat doběhnout, i když jsou patnáctkrát pomalejší než naše referenční řešení.
Úkol 1 – Sekvence [3b]
Začneme rozcvičkou. Na vrcholu zásobníku je kladné číslo k. Nahraďte jej sekvencí k až 0, včetně.
Před číslem k mohou i nemusí být další hodnoty. Musí zůstat nezměněny. Na zásobník se vždy vejde aspoň 1000 + k dalších čísel.
42 42 3
42 42 3 2 1 0
Úkol 2 – Řazení [4b]
Na vrcholu zásobníku naleznete číslo k (k ≥ 1), a pod ním dalších k čísel. Na zásobníku nic jiného není. Seřaďte celý zásobník s výjimkou horního čísla k (počtu prvků) od nejmenšího na dně po největší navrchu. Počet prvků k na vrcholu zásobníku odstraňte, nezatřizujte jej.
Čísla k seřazení na zásobníku mohou být libovolná, zejména upozorňujeme, že by program měl umět zpracovat i číslo -263. Univerzální duplikaci, která zduplikuje libovolná čísla, naleznete v řešení předchozí části.
3 4 -4 1 1 5
-4 1 1 3 4
Úkol 3 – Počet čísel na zásobníku [4b]
V předchozím úkolu jsme dostali počet čísel na zásobníku šikovně připravený. To je ale pěkný podvod, při normálním použití nám toto nikdo nedá. Je čas to vyřešit.
Přidejte na zásobník jedno číslo: počet čísel při začátku běhu programu. Zásobník před tímto číslem musí zůstat zachován. Zásobník na vstupu není prázdný, vždy je na něm alespoň jedno číslo.
Čísla na zásobníku mohou být libovolná v celém rozsahu znaménkových 64-bitových čísel. Univerzální duplikaci, která zduplikuje libovolná čísla, je v řešení předchozí části.
1 356 -2
1 356 -2 3
 36-3-X1 Výlet do Japonska (10 bodů)
36-3-X1 Výlet do Japonska (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
Kevin je na školním výletu do Japonska. A protože let do Japonska je jaksi…dlouhý, rozhodl se, že se během něj naučí pár slovíček. Na letišti si koupil slovník a teď si v něm listuje.
Kevin se učí slova následujícím způsobem: Opakovaně se učí slabiky (posloupnosti znaků), na které narazí ve slovníku. Slovo potom umí vyslovit, když ho umí rozdělit na slabiky, které umí vyslovit. (Tyto slabiky se ale nesmí překrývat.)
Kevina by zajímalo po každé naučené slabice, kolik slov již umí vyslovit. Prozradíte mu to?
Počítejte s tím, že 1 ≪ |Smax| ≪ N ≪ Q. Každá hodnota je řádově větší než předchozí: Malá konstanta, délka nejdelšího slova, počet slov, počet naučených slabik.
Slova: konnichiwa sumimasen ichi sushi shinkansen Naučené slabiky: shi su nkan s en ic umimase
0 1 1 1 2 2 2
Nejdřív Kevin bude umět vyslovit |su|shi| po dvou naučených slabikách.
Po pěti naučených slabikách bude umět i |shi|nkan|s|en|.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-3-S Učíme klasifikátory (12 bodů)
36-3-S Učíme klasifikátory (12 bodů)
Právě čtete třetí díl seriálu. Pokud jste předchozí díly neřešili, pro pochopení následujících odstavců je vhodné si je přinejmenším přečíst. Navíc je stále možné odevzdávat úlohy z nich za polovinu bodů.
V tomto dílu seriálu se podíváme na nejběžnější úlohu strojového učení, kterou je klasifikace.
Klasifikace
O klasifikaci jsme se bavili už v prvním dílu seriálu. Úkolem je přiřadit vstupním datům jednu z předem daných kategorií. Například dostaneme obrázek a máme určit, jestli se na něm nachází pes, nebo kočka. Nebo dostaneme umělecké dílo a máme určit, jakým stylem je nakresleno.
Pro začátek se spokojíme s klasifikací do dvou tříd, později si ukážeme rozšíření na více tříd. Jak toho docílit? Když nevíme, tak zkusme upravit model, který již máme – lineární regresi. Úprava bude postavená na jednoduché myšlence. Výstup lineární regrese proženeme nějakou funkcí, abychom z něj zjistili, která třída je pravděpodobnější. Této funkci budeme říkat aktivační funkce.
Po této aktivační funkci budeme chtít, aby dávala pravděpodobnostní distribuci do 2 tříd (Bernoulliho distribuci, viz dále). Jelikož klasifikujeme do dvou tříd, tak nám stačí jedna pravděpodobnost, druhá se jednoduše dopočítá jako jedna minus první pravděpodobnost. Z toho vyplývá, že výstup funkce musí být v intervalu <0,1>. Jinými slovy, vysněná funkce bude dávat pravděpodobnost, že dato patří do první třídy.
Naše vysněná funkce se bude nazývat sigmoida (anglicky sigmoid). Funkci budeme značit symbolem σ a má tento předpis:
| 1 |
| 1+e-x |
Z předpisu je vidět, že výstup funkce je v intervalu <0,1>. V minus nekonečnu funkce konverguje k nule a v kladném nekonečnu k jedné. V bodě nula je funkce rovna 0.5, což intuitivně odpovídá, že v bodě nula se mění, jaká třída bude predikována.
Pro shrnutí uvedeme přesný vzorec pro predikci, když známe optimální váhy w:
| 1 |
| 1+e-x ·w |
kde x ·w je skalární součin vektorů x a w, což je předpis lineární regrese, když bias přidáme jako novou váhu do vektoru w. Místo skalárního součinu si tam můžete představit součet z prvního dílu seriálu. Pro větší přehlednost jsme použili tento zápis.
Distribuce
Před chvílí jsme zde šermovali se slovem distribuce, ale tento termín jsme nevysvětlili. Nyní tento nedostatek napravíme. Distribuce (též pravděpodobnostní rozdělení) je funkce, která přiřazuje každému elementárnímu jevu hodnotu (pravděpodobnost) v intervalu <0,1>. Dále musí platit, že součet pravděpodobností všech jevů se rovná jedné. V našem případě jsou elementární jevy třídy, které predikujeme.
Bernoulliho distribuce
Později (pro derivování chybové funkce) budeme potřebovat generovat úplnou distribuci, neboli chceme najít funkci, které když řekneme, že chceme pravděpodobnost pro první třídu, tak nám ji vydá, a podobně pro druhou třídu. Tedy chceme najít předpis funkce, která nám na dotaz na první třídu vydá hodnotu σ(x) a pro druhou třídu 1 - σ(x), či obráceně podle toho, jak si očíslujeme třídy. Naštěstí Bernoulliho distribuci jde vcelku jednoduše (možná trochu trikově) zapsat jako:
kde y je výstup lineární regrese na nějakém datu a t je třída (0 nebo 1), na kterou se ptáme.
Maximálně věrohodný odhad
Dobrá, máme funkci, která dává distribuci a kterou chceme optimalizovat, ale jakou máme použít chybovou funkci? U lineární regrese jsme používali chybovou funkci MSE, ale zatím jsme se vůbec nezabývali tím, kde se vzala a proč je to dobrý nápad. Nyní ukážeme, jak se dostat k chybové funkci, a nastíníme i, jak jsme se dostali k MSE.
Mějme dataset příkladů X = { x1, …, xn } náhodně a nezávisle vybraných dat z distribuce pdata. Samotnou distribuci pdata neznáme. Naším cílem je najít distribuci pmodel (x;w), která bude co nejvíce odpovídat distribuci pdata, kde x je vstupní dato a w jsou váhy. Jak ale bylo řečeno, my distribuci pdata neznáme, známe jen množinu příkladů X náhodně vybraných z této distribuce.
Jelikož chceme namodelovat distribuci pmodel , potřebujeme nějakou distribuci vyrobit z datasetu X. Tuto distribuci budeme značit jako pˆdata a bude se nazývat empirická distribuce (empirical distribution). Empirická distribuce se vytvoří vcelku intuitivně a kdybyste to dostali za úkol, tak byste přišli na stejný výpočet. Spočítáme, kolikrát se v datasetu vyskytuje daná třída, a tento počet se vydělí počtem příkladů v datasetu. Tedy pokud v datasetu máme 50 obrázků kočiček a 150 obrázků pejsků, tak empirická distribuce bude dávat pravděpodobnost 0.25 (25 %) pro kočičky a 0.75 (75 %) pro pejsky.
Předpokládáme, že tato empirická distribuce pˆdata bude co nejvíce podobná distribuci pdata a tedy dává smysl modelovat distribuci pmodel tak, aby co nejvíce odpovídala empirické distribuci pˆdata. Pokud by tento předpoklad neplatil, tak z podstaty věci by žádné strojové učení nefungovalo.
Dále si trochu více povíme, co je to distribuce pmodel a proč jsme ji takto složitě definovali jako funkci „dvou“ parametrů. pmodel (x;w) je parametrizovaná rodina distribucí, kde w jsou váhy či parametry distribuce. Rodina distribucí je určitá množina distribucí daného typu. Například rodina Bernoulliho distribuce, která modeluje pravděpodobnost dvou tříd a má jeden parametr, který určuje pravděpodobnost první třídy. My ve výsledku chceme namodelovat určitou (např. Bernoulliho) distribuci, ale nesmíme zapomínat, že trénujeme váhy w lineární regrese, a teprve z výstupu lineární regrese vytváříme distribuci.
Pokud máme fixní váhy w, tak pmodel (x;w) nebo prostě pmodel (x) je pravděpodobnost, že dané dato bude vygenerováno z dané třídy. Například pokud bychom klasifikovali do 3 tříd, první třída může mít pravděpodobnost 0.3, druhá 0.5 a třetí 0.2.
Pokud místo toho máme fixní vstupní data X, tak
| n |
| i=1 |
se nazývá věrohodnostní funkce (likelihood function nebo jen likelihood). Pozor na to, že věrohodnostní funkce není pravděpodobnostní distribuce, protože i když jsou hodnoty mezi 0 a 1, nemusí se sečíst na jedničku. Vcelku dává smysl, že to není pravděpodobnostní funkce. Při učení modelu totiž hledáme takové váhy w, že dostaneme-li dato x, bude pravděpodobnost cílové třídy co největší (nejlépe 1).
Zde stojí za zmínku, přes co počítáme součin (velké písmeno ∏). Je to součin přes náš dataset – empirickou distribuci pˆdata (distribuci pdata neznáme).
Nyní chceme maximalizovat věrohodnostní funkci (maximum likelihood estimation), a to znamená, že chceme najít takové váhy w, které maximalizují věrohodnostní funkci. Čím větší je věrohodnostní funkce, tím více se naše distribuce pmodel bude přibližovat k empirické distribuci pˆdata. Samozřejmě bychom se chtěli přiblížit k reálné distribuci pdata, ale tu neznáme.
| n |
| i=1 |
Funkce argmaxw plní účel vybírání nejlepších vah w. Můžete si to představit tak, že argmaxw projde všechny možné váhy w a vybere tu, která maximalizuje věrohodnostní funkci. Samozřejmě by toto bylo moc pomalé, tak místo úplné metody projití všech vah při implementaci použijeme SGD algoritmus z minulého dílu seriálu.
Nyní si trochu budeme hrát s výrazem. Nejdříve můžeme výraz zlogaritmovat. Když výraz zlogaritmujeme, maximum se nezmění, protože logaritmus je rostoucí funkce. Navíc logaritmus dokáže součin převést na součet, což se velice hodí, protože součinem bychom mohli rychle podtéct přesnost floatových čísel. Získáme:
| n |
| i=1 |
| n |
| i=1 |
Nyní zbývá poslední krok a to převést maximalizaci na minimalizaci. Tento krok se může zdát zbytečný, ale když máte již naimplementované algoritmy pro minimalizaci, tak proč je nevyužít. Navíc se dobře o tom přemýšlí, jako o minimalizaci chyby. Převedení se udělá jednoduše, budeme sčítat záporná čísla:
| n |
| i=1 |
| n |
| i=1 |
Poslednímu výrazu se říká negative log-likelihood (NLL) a toto je naše hledaná chybová funkce. Když výraz trochu upravujeme v argminw dokážeme dostat cross-entropy a KL divergenci.
Toto se hodí vědět, protože i když předpisy funkcí NLL, cross-entropy a KL divergence se liší, ve skutečnosti se jedná o stejnou chybovou funkci. Abychom byli přesní, tak dané funkce negenerují stejné hodnoty, ale generují stejné minima a maxima. Dále když narazíte na různé články, budou uvádět, že použily danou chybovou funkci, ale ve skutečnosti je to ekvivalentní s NLL.
Musíte se ale mít na pozoru, protože pokud framework jako třeba PyTorch implementuje více takových funkcí, většinou to není jen tak. Tvůrci knihoven nejsou hloupí a většinou se tyto funkce liší tím, co máte dávat za vstup dané chybové funkci.
Znovu derivujeme
Výborně, máme chybovou funkci (negative-log likelihood), aktivační funkci (sigmoidu) a máme předpis funkce, která z aktivační funkce dává pravděpodobnostní distribuci. Samozřejmě mohli bychom mít aktivační funkci, která dává pravděpodobnostní distribuci a poslední krok by byl zbytečný, ale nyní máme specifický případ. Máme i obecný optimalizační algoritmus na hledání minima chybové funkce (SGD) a mohli bychom říct, že jsme hotovi. Skoro ano, ale potřebujeme vypočítat derivaci chybové funkce a jelikož součástí chybové funkci je sigmoida, nebude to úplně triviální.
Chceme tedy minimalizovat negative-log likelihood pravděpodobnostní distribuce:
kde funkce p dává pro jednotlivé třídy pravděpodobnosti toho, že model dostane vstupní dato x s váhami w. Kdybychom chtěli být formálnější, jedná se o podmíněnou pravděpodobnost výstupních tříd, přičemž podmínkou je, že dostaneme na vstupu vstupní dato x s váhami w.
Nyní si rozepíšeme funkci p:
 Tato část je technická a pokud jí nebudete úplně chápat,
můžete ji přeskočit až k následujícímu nadpisu.
Důležitý je výsledek derivace.
Tato část je technická a pokud jí nebudete úplně chápat,
můžete ji přeskočit až k následujícímu nadpisu.
Důležitý je výsledek derivace.
Teď už máme vše připraveno a můžeme začít derivovat. Budeme počítat derivaci podle jedné váhy wi, a pak z toho vykoukáme, jak má vypadat celý gradient podle vah.
| ∂ |
| ∂wi |
| ∂ |
| ∂wi |
kde y = x ·w (předpis lineární regrese).
Nyní můžeme logaritmy derivovat odděleně, protože derivace součtu je součet derivací. Zároveň použijeme řetězové pravidlo pro derivaci složené funkce. To říká, že
| ∂ |
| ∂x |
| ∂f |
| ∂g |
| ∂g |
| ∂x |
Toto pravidlo použijeme několikrát za sebou. Zatím budeme derivovat jen první logaritmus.
| ∂ |
| ∂wi |
| ∂ |
| ∂wi |
| ∂ |
| ∂σ(y) |
| ∂ |
| ∂wi |
| ∂ |
| ∂σ(y) |
| ∂ |
| ∂y |
| ∂ |
| ∂wi |
| ∂ |
| ∂σ(y) |
| ∂ |
| ∂y |
| ∂ |
| ∂wi |
Nyní stačí vypočítat jednotlivé derivace a pak je pronásobit mezi sebou. Začneme jednoduše s první derivací logaritmu. Budeme uvažovat, že logaritmus je o základu e (přirozený logaritmus). Použitím jiného logaritmu se minimum nezmění a přirozený logaritmus se jednoduše derivuje. Derivace přirozeného logaritmu ln x se rovná 1 / x, tedy
| ∂ |
| ∂σ(y) |
| 1 |
| σ(y) |
To šlo hladce, nyní se vrhneme na derivaci sigmoidy. Nejdříve použijeme derivaci podílu, která je rovna:
| ∂ |
| ∂x |
| f(x) |
| g(x) |
| f'(x) g(x) - f(x) g'(x) |
| g(x)2 |
Dále derivace funkce e-x je -e-x. Tedy derivace pro naši sigmoidu bude:
| ∂ |
| ∂y |
| ∂ |
| ∂y |
| 1 |
| 1+e-y |
| e-y |
| (1+e-y)2 |
Nyní trochu budeme upravovat výraz, abychom se dostali k jednoduššímu tvaru.
| e-y |
| (1+e-y)2 |
| 1 |
| 1+e-y |
| e-y |
| 1+e-y |
První zlomek je roven σ(y). Druhý budeme dál upravovat tak, že k němu přičteme a zase odečteme jedničku. To je korektní operace, a pomůže nám dojít k hezkému výsledku:
| e-y |
| 1+e-y |
| -1 - e-y + e-y |
| 1+e-y |
| 1 |
| 1+e-y |
Získali jsme tedy:
| ∂ |
| ∂y |
Poslední derivace, kterou potřebujeme spočítat, je již jednoduchá (to už je jen lineární regrese):
| ∂ |
| ∂wi |
Nyní všechny derivace spojíme dohromady a dostaneme:
| ∂ |
| ∂wi |
| 1 |
| σ(y) |
Derivace druhého logaritmu je už jednoduchá, jen si musíme dávat pozor na znaménko minus:
| ∂ |
| ∂wi |
| 1 |
| 1 - σ(y) |
| ∂ |
| ∂wi |
| 1 |
| 1 - σ(y) |
| ∂ |
| ∂wi |
| 1 |
| 1 - σ(y) |
Nakonec sečteme obě derivace a dostaneme:
| ∂ |
| ∂wi |
Vypočítaná derivace
Výsledná derivace podle váhy wi je:
což se dá přepsat jako:
kde p je predikce pro dato x a t je třída, kterou chceme predikovat (0 nebo 1). Pozornější z vás již si mohli všimnout, že toto jsme někde viděli. Ano, výsledná derivace vychází stejně jako u lineární regrese. Náhoda? Úplně ne, ale proč to tak je, nebudeme rozebírat.
Výsledná derivace vychází stejně pro všechny váhy wi, takže gradient jde zapsat jako:
Modelu, který používá sigmoidu a negative-log likelihood se říká logistická regrese.
Úkol 1 – Logistická regrese [2b]
Naprogramujte model logistické regrese. Model se bude trénovat pomocí
minibatch SGD. Pro každý minibatch spočítáte gradient a upravíte váhy.
Pro lehčí implementaci jsme připravili
šablonu,
která načítá různé parametry
jako je learning rate, počet epoch, velikost minibatche.
U komentářů, kde v závorce je napsáno (SGD), tak lze zkopírovat
z minulého dílu, kde jste implementovali minibatch SGD pro lineární regresi.
Ukázky použití (výstupy byste měli mít stejné):
python logistic_regression.py --epoch 4
Epoch 1: train loss 0.718978 acc 46.00, test loss 0.772734 acc 32.00
Epoch 2: train loss 0.684518 acc 60.00, test loss 0.739608 acc 36.00
Epoch 3: train loss 0.652850 acc 68.00, test loss 0.709127 acc 50.00
Epoch 4: train loss 0.623763 acc 76.00, test loss 0.681133 acc 54.00
python logistic_regression.py --epoch 4 --batch_size 5
Epoch 1: train loss 0.684218 acc 60.00, test loss 0.739269 acc 36.00
Epoch 2: train loss 0.623205 acc 76.00, test loss 0.680583 acc 54.00
Epoch 3: train loss 0.571590 acc 86.00, test loss 0.630870 acc 66.00
Epoch 4: train loss 0.527781 acc 94.00, test loss 0.588775 acc 82.00
Více tříd
Nyní se podíváme, jak rozšířit logistickou regresi do více tříd. Vyvstává otázka, zda jde pomocí binárních klasifikátorů rozdělit data do více tříd. Odpověď zní ano a je několik různých způsobů, jak toho dosáhnout.
Jeden způsob je použít one-vs-rest klasifikaci nebo nazývané také jako one-vs-all.
Pro každou třídu naučíme binární klasifikátor, který dokáže rozlišit
danou třídu od ostatních.
Tedy pro třídu 1 naučíme (model) klasifikátor, který dokáže rozlišit třídu 1 od
tříd 2 až k. Nápodobně pro třídy 2, 3, …, k.
Při predikci se udělá k predikcí (predikce pro každý model) a model, který si je nejvíce
jistý, že dané dato patří do dané třídy, je naše predikce.
Vybrání „nejjistější“ predikce se dá udělat například pomocí funkce argmax
z knihovny numpy (nebo pomocí obyčejného for cyklu).
Nevýhoda je, že musíme naučit k modelů, ale výhoda je, že můžeme použít
už náš naprogramovaný model.
Poté si můžete uvědomit, že daný přístup nemusí fungovat nejlépe, protože třídy se můžou mezi sebou různě překrývat a one-vs-rest je nemusí klasifikovat nejlépe. Proto existuje druhý přístup, který se nazývá one-vs-one. Ten funguje následovně. Pro každou dvojici tříd naučíme binární klasifikátor, který dokáže rozlišit dané dvě třídy. Tedy pro třídy 1 a 2 naučíme (model) klasifikátor, který dokáže rozlišit třídu 1 od třídy 2. Nápodobně pro třídy 1 a 3, 1 a 4, …, k-1 a k. Zde je vidět, že musíme naučit k ·(k-1) / 2 modelů, ale nemusí to být až tolik špatné, protože každý model se učí na méně datech (jen na datech z daných 2 tříd). Při predikci se udělá k ·(k-1) / 2 predikcí a výsledná predikce je třída, která zvítězí nejvíce krát. Neboli každý model hlasuje pro jednu ze dvou tříd. Poté všechny hlasy sečteme a třída s nejvíce hlasy je naše predikce.
Úkol 2 – Binární klasifikace do více tříd [5b]
Naprogramujte binární klasifikaci do více tříd pomocí one-vs-rest a one-vs-one. Pro lehčí implementaci jsme připravili šablonu, která načítá různé parametry, jako je počet klasifikačních tříd a způsob klasifikace (one-vs-rest nebo one-vs-one).
Ukázky použití (výstupy byste měli mít stejné, u typu one-vs-rest se pravděpodobnosti můžou lehce lišit):
python multiclass_classification_binary.py --type ovo --test
1 5 6 9 6 8 3 3 4 0
7 4 7 0 7 8 2 3 6 1
7 8 3 0 4 4 7 7 4 1
0 1 7 2 3 9 6 5 4 8
1 6 6 2 2 8 4 9 5 2
Predikované třídy pro první 10 dat:
3 5 1 5 7 1 6 8 2 5
python multiclass_classification_binary.py --type ovr --test
0.0034 0.0262 0.0785 0.3806 0.0002 0.3928 0.0005 0.0016 0.2000 0.0027
0.0072 0.0006 0.1154 0.0000 0.9011 0.7784 0.0009 0.0000 0.3307 0.0000
0.1100 0.7071 0.0007 0.0000 0.0412 0.0423 0.6696 0.1863 0.0008 0.0001
0.0000 0.0003 0.4934 0.0175 0.0085 0.8985 0.0201 0.0004 0.0050 0.5452
0.0071 0.1096 0.0085 0.0342 0.0000 0.0230 0.0002 0.5428 0.0459 0.0241
Predikované třídy pro první 10 dat:
5 4 1 5 7 1 6 0 2 1
Softmax
Předešlé způsoby rozšiřování binární klasifikace do více tříd jsou trochu neuspokojivé. Dané modely nevědí o tom, že se bude jednat o klasifikaci do více tříd, a proto nemůžou modely mezi sebou kooperovat.
Například pro správnou klasifikaci nějakého data může být zapotřebí upravit upravit váhy více modelů, což se nejspíše nikdy nestane, když budeme modely trénovat odděleně. Modely se snaží co nejlépe odlišit danou třídu od ostatních, což může jít i proti našemu cíli – klasifikace do více tříd. Budou se snažit odlišit outliery či zašuměná data, ale když je budeme učit naráz, tak dokážou toto „zjistit“ a výsledné predikce budou lepší.
Ukážeme aktivační funkci, která se bude jmenovat softmax a bude dávat pravděpodobnosti pro všechny třídy. Tento přístup bude vypadat podobně jako one-vs-rest, ale jednotlivé modely budou moci kooperovat díky tomu, že v gradientu loss funkce se projeví i ostatní modely, což s přístupem one-vs-rest nešlo.
| eyi | ||
∑
|
Kde yi je výstup lineární regrese pro třídu i a softmaxi říká pravděpodobnost, že dané dato patří do třídy i.
Když se na funkci podíváme, tak zjistíme, že sigmoida je speciální případ softmaxu, když máme jen dvě třídy. Sigmoida vrací pravděpodobnost první třídy a máme jen jeden model. Stejného výsledku dokážeme dosáhnout i pomocí softmaxu na dvou třídách a jednoho modelu. První model bude identický se sigmoidou a druhý model bude vracet konstantní nulu (softmax na dvou proměnných musí přijímat dva vstupy).
| ey |
| ey + e0 |
| 1 |
| 1 + e-y |
Dostali jsme přesně předpis sigmoidy.
Softmax používá jako chybovou funkci negative-log likelihood a derivaci vůči kategorické distribuci. Počítání gradientu již uvádět nebudeme, ale rovnou ukážeme, jak gradient chybové funkce se softmaxem vypadá:
kde 1t je vektor, který má na pozici t jedničku a na ostatních pozicích nuly, t je číslo (index) cílové (target) třídy, y jsou výstupy z lineárních regresí pro vstup (dato) x. y je tedy vektor velikosti počtu tříd. x je také vektor a jeho velikost je počet featur. Nepřekvapivě gradient vypadá dost podobně jako ostatní gradienty (u MSE a sigmoidy).
Jak se použije tento gradient pro úpravu vah jednotlivých modelů? Softmax bere na vstupu k vstupů a vrací k výstupů, které odpovídají pravděpodobnosti. i-tý výstup je spojený s i-tou třídou a danou hodnotu generuje i-tý model. Tedy i-té váhy modelu upravíte následovně:
kde wi jsou váhy i-tého modelu, α je learning rate a x je vstup. (softmax(y) - 1t)i znamená, že vezmeme i-tý prvek vektoru.
Nezapomeňte, že tuto úpravu můžete dělat až ve chvíli, kdy máte spočítané gradienty z celé batche.
Úkol 3 – Softmax [5b]
Naprogramujte model pro klasifikaci do k tříd pomocí softmaxu.
Model se bude trénovat pomocí minibatch SGD. Pro každý minibatch spočítáte gradient
a upravíte váhy. Pro lehčí implementaci jsme připravili
šablonu,
která načítá různé parametry, jako je learning rate, počet epoch, velikost minibatche.
U komentářů, kde v závorce je napsáno (SGD), tak lze zkopírovat
z minulého dílu, kde jste implementovali minibatch SGD pro lineární regresi.
Ukázky použití (výstupy byste měli mít stejné):
python softmax.py --epoch 4
Epoch 1: train loss 2.317040 acc 14.00%, test loss 2.394303 acc 6.00%
Epoch 2: train loss 2.225014 acc 18.00%, test loss 2.375340 acc 6.00%
Epoch 3: train loss 2.145034 acc 18.00%, test loss 2.362607 acc 8.00%
Epoch 4: train loss 2.073765 acc 26.00%, test loss 2.354539 acc 10.00%
python softmax.py --epoch 4 --batch_size 5
Epoch 1: train loss 2.224774 acc 16.00%, test loss 2.373263 acc 6.00%
Epoch 2: train loss 2.072504 acc 26.00%, test loss 2.352615 acc 10.00%
Epoch 3: train loss 1.954753 acc 28.00%, test loss 2.346726 acc 12.00%
Epoch 4: train loss 1.856579 acc 40.00%, test loss 2.349936 acc 10.00%
Gridsearch
Na závěr si ukážeme trochu automatizovanější způsob hledání dobrých hyperparametrů. Říká se mu gridsearch a funguje tak, že si zvolíme množinu hodnot pro každý hyperparametr a poté vyzkoušíme všechny kombinace těchto hodnot. Tedy pokud máme 3 hyperparametry a pro každý z nich vybereme 3 hodnoty, vyzkoušíme dohromady 33 = 27 modelů. Pro každou kombinaci spočítáme přesnost na validačních datech, a poté vybereme tu kombinaci, která má nejlepší přesnost. Nyní využijeme toho, že jednotlivé kroky v pipelině jsou pojmenované, protože díky nim teď můžeme definovat množinu parametrů pro gridsearch.
from sklearn.compose import ColumnTransformer
import sklearn.datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import \
PolynomialFeatures, MinMaxScaler
iris = sklearn.datasets.load_iris()
pipeline = Pipeline([
('ct', ColumnTransformer([
('min_max', MinMaxScaler(), [0, 1, 2, 3]),
])),
('poly', PolynomialFeatures()),
('lr', LogisticRegression()),
])
gridsearch = GridSearchCV(
pipeline,
param_grid={
'ct__min_max__feature_range': [
(0, 1), (-1, 1)
],
'poly__degree': [1, 2, 3],
'lr__C': [0.1, 1, 10],
},
cv=5,
scoring='accuracy',
verbose=1,
)
gridsearch.fit(iris.data, iris.target)
cv_results = gridsearch.cv_results_
for idx, param in enumerate(cv_results['params']):
cross_val = cv_results['mean_test_score'][idx]
print(
'Rank',
cv_results['rank_test_score'][idx],
f"Cross-val {cross_val * 100:.1f}%",
param
)
print("Best parameters:", gridsearch.best_params_)
Ukázkový program natrénuje pipelinu a při trénovaní vyzkouší různé kombinace hyperparametrů, ze kterých se vybere nejlepší. Parametry gridsearche se zadávají jako slovník, kde klíč je „cesta“, kde se má nastavit parametr. Dvěma podtržítky se oddělují jednotlivé názvy – ekvivalent lomítka v klasické cestě na souborovém systému. Cesta může být libovolně dlouhá, pokud chceme nastavit název parametru, který se nachází v nějakém objektu (příklad na column transformeru). Jako hodnota slovníku je pole hodnot, které chceme vyzkoušet.
Dodatky
Většinou se jako první model, který upravuje lineární regresi na klasifikaci, používá perceptron. Funguje velmi jednoduše, vezme výstup z lineární regrese a pokud je větší než nula, vrátí jedničku, jinak vrátí nulu (jednu nebo druhou třídu). Tento model jsme nezmiňovali, protože nemá úplně pěkné vlastnosti. Jeho nejhorší vlastnost je, že trénování se nemusí zastavit, pokud data nejsou lineárně separabilní. Například když si představíme data v rovině, musí existovat přímka, která rozdělí data, kde na jedné straně přímky jsou data jedné třídy a na druhé straně jsou data druhé třídy.
Nakonec ještě zbývá v rychlosti vysvětlit, kde se vzala chybová funkce MSE. Když použijeme princip maximální věrohodnosti s normálním rozdělením, postupnými úpravami dostaneme chybovou funkci MSE. Z normálního rozdělení vyplývá, že MSE se snaží mít všude stejný rozptyl (tedy mít všude stejnou chybu, ať predikujeme obrovské či miniaturní hodnoty). Toto nám občas samozřejmě nemusí vyhovovat. Řekněme, že máme callcentrum a chceme predikovat, kolik lidí zavolá. S MSE metrikou by byla stejně dobrá predikce 1 volajícího, když reálně volalo 11 lidí, jako predikce 101 volajících, když reálně volalo 111 lidí. Toto může být ve skutečnosti problém, protože když zaměstnáte jednoho člověka, aby odpovídal na dotazy zákazníků, a najednou jich zavolá 10krát více, tak většina se zákazníků nedovolá. Oproti tomu, zavolá-li 111 místo 101, už to pro nás nemusí být velký problém.
Tedy občas se hodí povolovat větší rozptyl chyby, když predikujete větší hodnoty, a menší rozptyl u menších predikovaných hodnot. To se dá modelovat pomocí Poissonova rozdělení a i v scikit-learn je naimplementovaný model s tímto rozdělením – PoissonRegressor.
Úkol 4 – Soutěžní úloha [3b]
Jako poslední úkol bude znovu soutěžní úloha. Z technických důvodů je soutěž zadaná jako samostatná open-datová úloha 36-3-S2, kterou najdete níže. Zdrojový kód soutěžního programu ale přidejte do ZIPu s řešením seriálu.
Všechny úlohy z tohoto seriálu odevzdávejte dohromady v jednom zazipovaném archivu. Termín odevzdání je 7. dubna ve 32:00 (tedy další ráno v 8:00). Poté lze odevzdávat za snížený počet bodů až do konce ročníku.
Pokud jste text dočetli až sem, tak vám velice gratuluji! Mějte se krásně a v příštím dílu se podíváme na rozhodovací stromy!
 36-3-S2 Soutěžní úloha seriálu (3 body)
36-3-S2 Soutěžní úloha seriálu (3 body)
Z technických důvodů je 4. úkol seriálu oddělenou úlohou. Odevzdává se jako open-datová úloha 36-3-S2, ale prosíme přiložte do zazipovaného archivu k seriálu i svá řešení tohoto úkolu. Pokud to neuděláte, můžeme vám dodatečně body odebrat.
V této soutěži je povolené používat libovolné generalizované modely,
tedy libovolné modely ze scikit-learn z modulu sklearn.linear_model.
Je zakázáno používat jiné modely implementované
v knihovně scikit-learn jako rozhodovací stromy, MLP, …
Jak soutěž bude probíhat? Od nás dostanete trénovací a testovací data. Dále od nás dostanete šablonu, která si v případě potřeby data stáhne a načte vám data. U trénovacích dat budete mít k dispozici vstupní featury a výstupní hodnoty, ale u testovacích dat budete mít k dispozici jen vstupní featury. Vaším úkolem je natrénovat model na trénovacích datech a predikovat výstupní hodnoty pro testovací data. Dataset můžete různě transformovat (augmentovat), ale nesmíte si přidávat další externí data do trénovacího datasetu. Všechny výstupy musí být generované vaším programem. Toto pravidlo nezakazuje mít v programu pravidla, která výstupy upravují. Tyto predikce poté odevzdáte do odevzdávátka.
Vaším úkolem je vypredikovat, jestli daný pacient má poruchu štítné žlázy.
Pokud vaše řešení bude splňovat, že na testovacích datech budete mít přesnost (accuracy) minimálně 96% (této hodnotě budeme říkat práh), tak dostanete 3 body. Tím ale zábava teprve začíná, protože tímto krokem jste se kvalifikovali do soutěže.
Daná přesnost se může zdát vysoká, ale když většina pacientů nemá problém se štítnou žlázou (přes 90%), tak se musí vyšší přesnost. Očekáváme vaší férovost a že nebudete postupnými úpravami výstupu zjišťovat, která odpověď je správná.
V soutěži budete soutěžit s ostatními řešiteli až o další 3 bonusové body. Abyste věděli, jak si stojíte, tak k této úloze je i dynamická výsledkovka. Na této výsledkovce uvidíte svou accuracy metriku na testovacích datech nebo hodnotu prahu, podle toho, jaká hodnota je horší. Dále na této výsledkovce budete řazeni podle accuracy metriky na testovacích datech. Pokud jste v soutěži, tak sice neuvidíte accuracy metriku, ale pořád budete vědět, kolik lidí je lepší než vy.
Bonusové body se budou udělovat podle následujícího kritéria: Nejlepší první čtvrtina řešitelů řazená podle accuracy metriky, která se kvalifikovala do soutěže, dostane 3 body, druhá čtvrtina dostane 2 body a třetí čtvrtina dostane 1 bod. Bonusové body budou přiděleny po prvním deadlinu pro tento díl seriálu.
Hodně štěstí!