Pátá série třicátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 36-5-1: Opravování opravy vzducholodi
- 36-5-2: Polygloti
- 36-5-3: Všechny cesty vedou do Říma
- 36-5-4: Hackovaci soutez
- 36-5-S: Učení bez učitele
- 36-5-X1: Superstring
 36-5-1 Opravování opravy vzducholodi (Zadání)
36-5-1 Opravování opravy vzducholodi (Zadání)
Každé rozdělení řešení mezi organizátory můžeme ohodnotit dvěma čísly – počtem organizátorů K' a časem potřebným k opravení L'. Na K' máme zadaný ostrý limit Kmax := K, zato L' se snažíme získat co nejmenší.
Co kdybychom řešili o trochu jinou úlohu? Tentokrát budeme mít horní limit na L', a to Lmax, optimalizovat budeme pro změnu K'. Jinak řečeno, snažíme se řešení rozdělit mezi co nejméně organizátorů tak, aby jim opravování trvalo nejvýše Lmax mikrosekund.
Nějaký organizátor bude určitě muset opravit první řešení. Je jasné, že to bude první z jemu přidělených řešení, vybrat si můžeme jen to, kolik řešení opraví celkem. Určitě nic nezkazíme, pokud mu přidělíme tolik řešení, kolik jen můžeme – pokud na zbylé organizátory zbude méně řešení, tak zbylých organizátorů nemůže být potřeba více. Přidělíme mu tedy co nejvýše řešení a zbylá rozdělíme stejným způsobem. Můžeme tedy použít jednoduchý hladový algoritmus běžící v čase O(N).
Už víme, jak pro dané Lmax určit minimální K', ale my chceme pro dané Kmax určit minimální L'. K tomu využijeme binárního vyhledávání. Pomocí něj budeme hledat čas potřebný k opravení všech řešení. Dolní mez vyhledávání bude největší z časů T1, … , TN, zatímco horní mez bude jejich součet.
Mějme nějaký časový limit Lmax. Použijeme náš hladový algoritmus k spočtení minimálního počtu organizátorů K'. Pokud K' ≤ Kmax, tak Kmax organizátorů stihne všechna řešení v tomto čase opravit, hledaný minimální potřebný čas tedy bude Lmax nebo nižší, můžeme proto horní mez nastavit na Lmax. Naopak pokud K' > Kmax, tak v čase Lmax všechna řešení není možné opravit a musíme vyzkoušet vyšší časový limit. Nastavíme proto dolní mez na Lmax + 1.
Tím zjistíme, kolik času Kmax organizátorů potřebuje, aby opravili všechna řešení. Nakonec naposledy použijeme hladový algoritmus k tomu, abychom našli rozdělení, které vypíšeme. Počet kroků tohoto binárního vyhledávání bude logaritmický vzhledem k součtu T1, … , TN. V každém kroku použijeme hladový algoritmus, co běží v lineárním čase. Celkem tedy získáme časovou složitost O(N log S), kde S = T1 + ...+ TN je součet všech čísel na vstupu.
 36-5-2 Polygloti (Zadání)
36-5-2 Polygloti (Zadání)
Úlohu na vstupu snadno převedeme do řeči grafů: máme zadaný orientovaný graf a v něm nějaký startovní vrchol vs a cílový vrchol vc a chceme najít dvě cesty z vs do vc, které se co nejvícekrát rozdělí a zase potkají. Důležité je, že náš graf je speciální – všechny hrany jsou orientované směrem z vrcholu s nižším číslem do vrcholu s vyšším číslem. Jinými slovy, graf je acyklický, neboli DAG (z anglického directed acyclic graph). Nahlédneme totiž, že jakmile se z libovolného vrcholu po hranách vydáme pryč, už se do něj nikdy nemůžeme vrátit, a tedy tento vrchol nemůže být součástí žádného cyklu.
Úloha přímo vybízí k použití dynamického programování: není jasné, jak by takové optimální řešení mělo vypadat, a hladové přístupy stylu „najdi nejdelší cestu a pak k ní najdi druhou cestu s nejvíce rozděleními a spojeními“ zjevně nebudou dávat správné výsledky.
Pro zjednodušení popíšeme řešení, které pouze vypíše největší dosažitelný počet rozdělení. Lze ho upravit, aby umělo i zrekonstruovat nalezenou dvojici cest; pro detaily se podívejte do zdrojového kódu. Budeme chtít spočítat pole A, kde A[i] značí následující: ze všech dvojic cest, které začínají v vs a (obě) končí v i, vezmeme dvojici s největším počtem rozdělení a spojení, a tento počet chceme po doběhnutí programu mít spočítaný v A[i]. Po spočítání celého A pak jen vypíšeme A[vc] jako výstup programu.
Pro spočítání pole A se nám bude hodit předpočítat si odpovědi na dotazy typu „Kolik existuje různých cest z u do v?“. To uděláme jednoduchým dynamickým programem, který postupně spustíme pro každé u. Nejprve vyřešíme okrajové případy: z u do u existuje právě jedna cesta (ta nulové délky), kdežto z u do v < u existuje vždy nula cest. Teď postupně spočítáme počet cest do v = u + 1, u + 2, … , n. Pro daný vrchol v se podíváme na všechny jeho předchůdce p1, … , pk – tedy vrcholy ze kterých do v vede hrana. Do nich už máme počet cest z u správně spočítaný, a počet různých cest z u do v je přesně součet počtů cest z u do p1, p2, … , až pk.
Tento předvýpočet nám zabere O(n + m) = O(m) času pro jedno u, a tedy O(nm) dohromady (za předpokladu, že graf je souvislý, a tudíž n = O(m)). Jeho výsledkem je dvojrozměrná tabulka T, kde v T[u][v] máme spočítaný počet různých cest z u do v.
Nyní už můžeme přejít k samotnému výpočtu pole A. Připomeňme, že A[i] značí počet rozdělení nejlepší dvojice cest začínajících v vs a končících ve vrcholu i. Jak z hodnot A[1], … , A[i - 1] spočítat A[i]? Snadno: libovolná dvojice cest, která se potkává v i ≠ vs, se potkává v nějakém j < i, odkud pak obě cesty nějak pokračují do i. Můžeme tedy začít s A[i] = 0, pak vyzkoušet všechny j < i a rozlišit tři případy podle počtu cest vedoucích z i do j:
- Pokud T[j][i] ≥ 2, pak A[i] můžeme zlepšit na A[j] + 1, jelikož můžeme nejlepší dvojici cest do j prodloužit do i a vyrobit přitom další rozdělení.
- Pokud T[j][i] = 1, pak A[i] můžeme zlepšit na A[j], jelikož můžeme nejlepší dvojici cest do j prodloužit do i, ale bez vyrobení dalšího rozdělení.
- Pokud T[j][i] = 0, pak pro toto j nic neděláme, jelikož cesty do j nejdou prodloužit do i.
Můžeme tedy projít všechna i = 1, … , n a pro každé postupně vyzkoušet všechna j = 1, … , i - 1. Takto v čase O(n2) spočítáme celé A. Časová složitost celého algoritmu je tak O(nm + n2) = O(nm), paměťová O(n2).
Ještě drobný detail: různých cest mezi dvojicí vrcholů může být řádově 2n, takže pro počítání T přesně bychom museli pracovat s O(n)-bitovými čísly. Tomu se vyhneme tak, že všechny hodnoty větší než 2 nahradíme při ukládání do T dvojkou. Chování algoritmu se tím nijak nezmění.
Kvadratické řešení
 Složitost O(nm) stačila na plný počet bodů, jde to však i lépe. Ukážeme si řešení, které pracuje v čase O(n2), což je výrazně lepší pro husté grafy.
Složitost O(nm) stačila na plný počet bodů, jde to však i lépe. Ukážeme si řešení, které pracuje v čase O(n2), což je výrazně lepší pro husté grafy.
Stále budeme počítat pole A, ale bez pomoci tabulky T, jejíž konstrukce nás brzdila. Místo toho si pro každý vrchol v budeme pamatovat množinu M[v] všech vrcholů u takových, že A[u] = A[v] a z u existuje cesta do v. Platí totiž následující tvrzení:
Tvrzení. Mějme vrchol v a jeho předchůdce p1, … , pk a označme největší hodnotu A[pi] jako x. Pak buď A[v] = x, nebo A[v] = x + 1 a druhá situace nastane právě tehdy, když pro dva různé předchůdce pi, pj s A[pi] = A[pj] = x platí, že M[pi] ∩M[pj] ≠ ∅.
Pojďme se přesvědčit o jeho pravdivosti. Určitě A[v] ≥ x, jelikož nejlepší dvojici cest do nějakého předchůdce x umíme vždy prodloužit až do x. Nerovnost platí ostře právě tehdy, když existuje nějaký vrchol w s A[w] ≥ x, ze kterého existují dvě cesty do v. Nutně ale musí platit A[w] ≤ x (jelikož optimální dvojice cest do w jde prodloužit do v a tudíž i nějakého pi), a tudíž A[w] = x. Víme též, že ony dvě cesty z w do v se musejí spojit až v x, jinak by už nějaké pi mělo A[pi] = x + 1, což není možné. Jinými slovy, musejí existovat dva různí předchůdci v dosažitelní z w. Označme je pi a pj. Díky dosažitelnosti platí A[pi] = A[pj] = x. Z definice M ale plyne, že w ∈M[pi] a w ∈M[pj], přesně, jak jsme chtěli.
Tvrzení nám dává jednoduchý návod na algoritmus: postupně pro každé i = 1, … , n počítáme A[i] a ruku v ruce s ním i M[i]. Množiny M budeme reprezentovat pomocí hešovacích tabulek. Pro každé i vždy nejprve spočítáme sjednocení S všech M[p1], … , M[pk]; přitom už rovnou kontrolujeme, zda se nám nějaký prvek objevil dvakrát. Pokud ne, pak dle předchozího tvrzení víme, že A[i] = x, a můžeme položit M[i] = S. Pokud ano, pak naopak víme, že A[i] = x + 1, a jelikož jediný vrchol s A[·] = x + 1, ze kterého je dosažitelný vrchol i, je vrchol i samotný, položíme M[i] = {i}.
Jaké má toto řešení časovou složitost? Na první pohled by se mohlo zdát, že jsme si vůbec nepomohli. Každé M[i] obsahuje až n prvků a za každou hranu tak můžeme provést až Θ(n) práce při sjednocování. Pokud ale sjednocování budeme dělat chytře, a zastavíme se hned, jak objevíme duplicitní prvek, pak v každém vrcholu sjednocováním strávíme nanejvýš O(n) času – buď totiž nenarazíme na duplikát a pak jsme zákonitě museli vyrobit množinu s nejvýše n prvky, nebo jsme na duplikát narazili, ale opět nanejvýše po probrání n prvků. Celková časová složitost pak tedy opravdu je O(n2). (Přesněji řečeno se jedná o průměrnou časovou složitost, protože hešujeme.)
 36-5-3 Všechny cesty vedou do Říma (Zadání)
36-5-3 Všechny cesty vedou do Říma (Zadání)
Lehká varianta
Nejdřív vyřešme zjednodušenou variantu – vzdálenost Adama i Kačky od Říma je stejná, tedy Rb = Rm. (Čili oba dojdou do Říma za stejný počet kroků.) Všimněme si, že od prvního společného vrcholu budou jejich cesty stejné – z každého vrcholu je jednoznačně určeno, kam cesta bude pokračovat, až dojdou do Říma. Tedy cesty budou mít dvě části – první rozdílnou a druhou od prvního společného vrcholu, kde se oba vždy budou vyskytovat ve stejných vrcholech.
Z toho se nabízí snadný algoritmus v čase O(Sb + Sm): Dokud Adam a Kačka nejsou ve stejném vrcholu, tak se oba přesunou do dalšího vrcholu. Jakmile se oba vyskytnou ve stejném vrcholu, tak máme první společný, a můžeme skončit. Udržujeme si jen aktuální pozici Adama a Kačky, takže se vejdeme do požadované O(1) paměti.
Zobecnění
Nicméně vzdálenost Adama a Kačky od Říma není stejná. To snadno opravíme. Nejdřív si simulací spočteme vzdálenosti Adama i Kačky od Říma. Nyní nám akorát stačí posunout vzdálenějšího od Říma o |Rm - Rb|. A potom můžeme použít algoritmus výše.
Zjištění vzdálenosti od Říma zabere O(Rb + Rs), takže celý algoritmus potrvá O(Rb + Rs + Sb + Sm) = O(Rb + Rs). Navíc si udržujeme vzdálenosti od Říma a jejich rozdíl, takže se stále vejdeme do O(1) paměti.
Zlepšujeme
Předchozí řešení je pomalé v případě, kdy se Adamova a Kaččina cesta potkají relativně brzy, tedy když Rb a Rs je o hodně větší než Sb a Sm. Nyní si ukážeme řešení pracující v čase O(Sb + Sm). Opět zkusíme najít |Rm - Rb|, ale tentokrát na to půjdeme chytřeji. Předpokládejme, že Adam je od Říma dál. Nejdřív uděláme k kroků s Kačkou (hodnotu k určíme za chvíli) a zapamatujeme si, kde jsme skončili – označme tento vrchol vk. Poté budeme dělat nejvýš k kroků s Adamem. Pokud se po k' krocích dostaneme do vk, tak platí |Rm - Rb| = k - k', protože zbytek cesty je stejný. Pokud vk neprojdeme, tak víme, že alespoň jeden po k krocích neskončil ve společné části, neboli k < max(Sb, Sm).
Nejdřív se zbavme předpokladu, že Adam je od Říma dál. Pokud to neplatí, pak Kačka nemá šanci dohnat Adama. Proto můžeme vyzkoušet obě možnosti a nejvýš jedna vydá správný výsledek.
Ale jak si správně tipnout k, aby k ≥ max(Sb, Sm)? Budeme postupně zkoušet mocniny dvojky – nejdřív vyzkoušíme 1, potom 2, 4, 8, … Protože jsme se v předchozím pokusu netrefili, tak v posledním pokusu s kℓ kroky přestřelíme max(Sb, Sm) ani ne dvakrát:
| kℓ |
| 2 |
A kolik nás stálo zkoušení práce?
| kℓ |
| 2 |
Zde jsme využili vzorce pro částečný součet geometrické posloupnosti: 1 + 2 + 4 + 8 + ...+ 2n = 2n + 1 - 1.
Proto hledání rozdílu vzdáleností stihneme v čase O(kℓ) = O(max(Sb, Sm)). Po srovnání rozdílu |Rm - Rb| můžeme použit algoritmus v lehké variantě. Zároveň si ověřme, že používáme jen O(1) paměti. Stačí, když si budeme pamatovat:
- aktuální k
- kde Kačka aktuálně je a kolik kroků nám zbývá
- vrchol vk, kde Kačka skončila
- kde je právě je Adam a zbývající počet kroků
- aktuální |Rm - Rb|
Takže máme algoritmus s časem O(Sb + Sm) a O(1) pamětí.
 36-5-4 Hackovaci soutez (Zadání)
36-5-4 Hackovaci soutez (Zadání)
Segmentation fault (core dumped)
Než začneme úlohu řešit, musíme zjistit, co je s programem špatně – kde je v něm
zranitelnost. V případě našeho programu to bude velmi jednoduché, neboť se hned
na jednom z prvních řádků se volá funkce gets. Napovědět by nám mohlo, že
když si otevřeme manuálovou stránku téhle funkce pomocí man gets, popis
funkce začíná větou „Never use this function.“ Dokonce od verze C11 byla
funkce odstraněna ze standardu a od glibc 2.16 funkce není exportovaná
v headerech.
Proč je gets tak špatná? Jak známo, v C si musíme veškerou správu paměti
řešit sami. Vždy máme vyhrazenou nějakou část paměti a držíme si ukazatel na
její začátek. Abychom však s pamětí mohli správně pracovat, musíme si pamatovat
i to, jak je ta část paměti dlouhá, jinak hrozí, že omylem zapíšeme za ni a
přepíšeme cizí data. Všimněme si proto, že gets bere pouze jeden argument,
kterým je ukazatel na cílový buffer. Do něj pak zapisuje, dokud mu uživatel
posílá data, nehledě na tom, jestli už při tom nepřepisuje cizí paměť. Vzhledem
k tomu, že nikdy nebudete mít k dispozici nekonečnou paměť, gets vždy způsobuje tzv. buffer overflow.
Máme tedy buffer overflow na bufferu heslo a můžeme přepisovat
cokoliv, co se zrovna v paměti nachází za ním. Nejprve si všimneme, že buffer
heslo je lokální proměnná, a nachází se proto na zásobníku. Můžeme tedy
přepsat nějaká data na zásobníku, ale jaká? Vzpomeňte si na kuchařku
k této úloze, kde jsme si rozvržení zásobníku ukazovali.
Zásobník roste směrem k nižším adresám a náš buffer je úplně poslední věc na
zásobníku, proto je přímo za ním celý zbytek zásobníku.
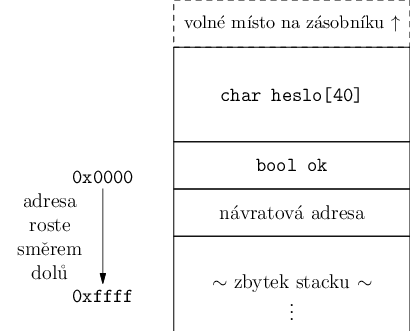
Možná by se slušelo si říct, jak vlastně taková pole fungují. Na první pohled se
to může zdát jako triviální otázka, ale bude se hodit. Intuitivně je pole nějaká
posloupnost políček stejného typu, přičemž ke všem políčkům můžeme přistupovat
v konstantním čase. Nás ale bude zajímat i implementace. Céčková pole jsou tak
jednoduchá, jak to jen jde. V proměnné heslo, která pole reprezentuje, je
uložený jen ukazatel na začátek místa vyhrazeného pro pole a operátor a[i]
je tak jen zkratka za *(a+i). Prostě k počáteční adrese pole přičteme index
(implicitně vynásobený velikostí políčka)
a vezmeme hodnotu z místa v paměti, kam ukazuje výsledný ukazatel.
To nám pomůže nahlédnout dvě věci. Jednak je zde dobře vidět, jak jednoduše k takovým přetečením dochází – když indexujeme pole, říkáme prostě „ukaž mi kus paměti o X míst dál“. Tam, když nejsme opatrní, může být už úplně něco jiného. Také vidíme, že i když stack roste směrem k nižším adresám, pole na něm uložená musí pořád růst stejně jako ta mimo zásobník – směrem k vyšším adresám. Když se předává pole jako argument, není totiž nikde specifikováno, jestli se jedná o pole na zásobníku nebo mimo něj.
Pojďme se tedy podívat, jak konkrétně bude vypadat zásobník, když do bufferu
heslo napíšeme třeba Ahoj!.
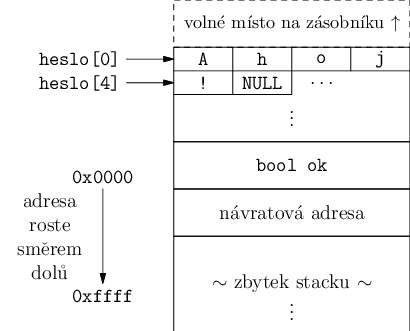
Z toho už je vidět, že když nám buffer přeteče a budeme se pokoušet napsat data
do paměti někam za něj, první věc, kterou přepíšeme, bude booleovská proměnná ok. V C neexistují opravdové booleany, ve skutečnosti jsou to celá čísla. Pokud
je v proměnné uložená 0, považuje se za false, jinak se považuje za true. Teď už tedy víme, jak získat první vlajku: potřebujeme přepsat hodnotu
proměnné ok na cokoliv jiného než nulu, která je v ní zpočátku uložená.
Teoreticky by nám tedy mělo stačit do bufferu heslo napsat 41×
libovolný znak (třeba A), tím buffer přeteče, přepíše hodnotu ok na
nenulovou a máme vyhráno. Stačit to ale nebude, protože proměnné typicky nejsou
v paměti uložené těsně za sebou, ale kompilátor se často snaží, aby proměnné
byly uložené na nějakých „kulatých“ adresách, takže mezi proměnnými může být
ponechané volné místo. To, kolik znaků musíme poslat, už lze ověřit
experimentálně; v našem případě to bude 48.
Hned další věc, kterou na zásobníku najdeme, je dvojice uložených hodnot
registrů rbp a rsp při volání funkce (hodnotu rbp jsme pro
jednoduchost v obrázcích výše neznázorňovali). Zajímat nás bude ta druhá
z nich, neboť se jedná o návratovou adresu. Jak jsme si pověděli
v kuchařce, návratové adresy jsou asi to
nejdůležitější, co se na zásobník ukládá. Když se na konci mainu zavolá
instrukce ret, vezme se posledních osm bytů ze zásobníku a na danou
adresu se skočí, ať je tam cokoliv. Proto když do programu hodíme Aček
příliš mnoho, program vyhodí Segmentation fault, čímž nám operační systém dává
najevo, že jsme se pokoušeli přistupovat k paměti způsobem, kterým nemáme.
V tomto konkrétním případě jsme se pokusili vykonat instrukci uloženou na
adrese 0x4141414141414141, kde bude s velkou pravděpodobností
nenaalokovaná paměť, kterou rozhodně nemáme právo spouštět.
Kdyby se nám tedy povedlo místo osmi Aček nahradit návratovou adresu
adresou nějakého spustitelného kódu, program na ni šťastně skočí a kód vykoná.
Přesně takový spustitelný kód přeci máme. Konkrétně funkci print_flag2,
která je za normálních okolností nedosažitelná. Stačí tedy prostě v našem
„hesle“ nahradit správnou osmice Aček její adresou. Jediné, na co je
potřeba si dát pozor, je tzv. endianita – čísla jsou na x86 little
endian, jako první je v paměti uložený nejméně významý byte, tedy ten,
který je ve standardním zápisu až poslední.
Je zde také jedna věc, kterou nám autor úlohy řešení značně zjednodušil.
Program, který běží na serveru, je totiž kompilovaný s parametrem -no-pie,
tedy že program nemá být Position Independent Executable. Dnes je
totiž poměrně častý default, že se programy kompilují tak, aby nezáleželo na
tom, na jakou adresu se program do paměti načte. Typicky se všechny skoky
v programu nahradí relativními (tedy místo „skoč na adresu X“ se použije
„skoč o X bytů dál/zpět“) a skoky na knihovní funkce se vyřeší
speciální tabulkou, kterou doplní linker/OS při startu programu. OS pak může
využít techniky ASLR (Address space layout randomization), tedy při
načítání programu do paměti ho prostě hodí na náhodnou adresu v paměti, aby bylo
daleko obtížnější skákat do kódu a dělat neplechu. Tahle funkce byla ale při
kompilaci vypnutá, takže adresy všech funkcí známe dopředu a můžeme je zjistit
například pomocí příkazu objdump -S, který nám vypíše disassembly
strojového kódu, včetně názvů funkcí a adres, na kterých jsou umístěné.
Disassembly je převedení strojového kódu (tedy jedniček a nul, kterým rozumí procesor) na assembly – lidsky čitelný seznam instrukcí, které procesor vykonává. V našem případě je to užitečné jen pro získání adresy funkce. V reálných Hackovacích soutěžích, ale i v reálné praxi, často nemáme k dispozici zdrojový kód programu, jen zkompilovanou binárku, takže musíme vyčítat co přesně kód dělá právě z jednotlivých instrukcí disassembly.
Teď ještě pár slov o mnoha různých způsobech, jak se od těchto teoretických poznatků dostat k vlajce. Vzhledem k tomu, že samotné provedení exploitu spočívá v poslání několika desítek konkrétních bytů, existuje mnoho způsobů, jak na to.
Ten technicky nejjednodušší způsob je prostě otevřít spojení se serverem pomocí
nc a nadatlovat byty ručně. U první vlajky je to proveditelné, protože
stačí napsat hodně Aček za sebou, u druhé vlajky je to horší, neboť asi
neexistuje žádné klávesnicové rozvržení, které by umělo napsat nulový byte. Můžeme
použít například příkaz printf nebo Python k vypsání divných znaků pomocí
escapování:
\x15\x12\x40\x00\x00\x00\x00\x00
Jedno z organizátorských řešení pak používá příkaz xxd pro převedení
z hexdumpu, což trochu vylepšuje čitelnost:
(
echo -n "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
xxd -r <<<"0: 0000 0000 0000 0001" # bool ok
xxd -r <<<"0: 0000 0000 0000 0000" # rbp
xxd -r <<<"0: 1512 4000 0000 0000" # rip
echo
) | nc vm.kam.mff.cuni.cz 13337
Upgradovat náš exploit můžeme přepsáním do Pythonu. Některé části payloadu
si tak můžeme nechat vygenerovat nějakou funkcí, což kód učiní trochu
čitelnějším. Také získáme trochu lepší kontrolu nad tím, jak a kdy se konkrétní
data pošlou na server. Druhé organizátorské řešení používá právě Python a
knihovnu sockets:
s = socket.socket(socket.AF_INET,
socket.SOCK_STREAM)
s.connect(("vm.kam.mff.cuni.cz", 13337))
s.recv(len("Zadejte heslo: "))
s.sendall(
b"a" * 56 +
0x401215.to_bytes(8, 'little') +
b"\n"
)
Zde nám Python pomůže v čitelnosti tím, že můžeme opakování Aček udělat
násobením stringů, také na převedení adresy funkce print_flag2 na
osmibytový little-endian integer můžeme použít funkci to_bytes.
Kde nám Pythoní sockets trochu práci přidělají, je přijímání výstupu
z programu. Funkce
recv
totiž přijímá vždy jen jeden packet, a když se stane, že server na druhé straně
odpověď rozdělí do více paketů, musíme recv zavolat víckrát. Nejlepší je ho
volat ve smyčce, dokud recv nevrátí prázdný bytearray, čímž zjistíme, že
se druhá strana odpojila.
Ti z vás, kteří se dočetli až sem, si asi říkáte, že je to všechno takové hrozně
zdlouhavé. Musíme dlouho rozmýšlet jak přesně jsou hodnoty v paměti uložené,
abychom se s adresou strefili do správného místa, nebo místo toho zdlouhavě
zkoušíme hádat počty Aček, než nám to vyjde. Také je to celé velmi
neprůhledné, program nám toho moc neřekne, jen občas spadne na segfault a po
dlouhém snažení třeba vypíše vlajku. Proto si ještě na konec představíme, jak se
dá úloha řešit snadno a rychle pomocí dvou nástrojů navíc – debuggeru gdb
a Pythoní knihovny pwntools.
První trik použijeme k rychlému zjištění, jaký je offset adresy v payloadu,
tedy, kolik Aček musíme napsat před adresu, aby se trefila na správné
místo. Použijeme k tomu funkci cyclic z pwntools. Tahle funkce nám
vygeneruje tzv. De Bruijnovu
posloupnost, tedy
posloupnost, kde se každé podslovo velikosti n (v našem případě 4) vyskytne
právě jednou. Nebudeme chtít posloupnost celou, bude nám stačit pouze její
prefix tak dlouhý, aby stačil na způsobení buffer overflow, 100 znaků by mělo
stačit. Délka prefixu se podává jako první argument funkci, která se dá také
zavolat z příkazové řádky pomocí pwn cyclic 100. Vygenerovanou sekvenci
si zkopírujeme do schránky.
Následně spustíme náš program v gdb zavoláním příkazu gdb
36-5-4-vuln. Poté, co se ocitneme v příkazové řádce debuggeru zavoláme příkaz
run a program se spustí. Ze schránky vložíme připravenou sekvenci a –
segfault. Tentokrát program nespadl úplně, ale debugger si ho drží pozastavený
ve stavu těsně před pádem, takže se můžeme podívat, jak přesně k pádu došlo.
Nejdřív použijeme příkaz disassemble, který nám vypíše (úplně stejně jako
objdump výše) disassembly, navíc se šipkou, která ukazuje na místo v kódu, kde se
program zarazil. Šipka ukazuje na instrukci ret na konci mainu, což
potvrzuje naši hypotézu uvedenou o pár odstavců výše. Adresa, na kterou se
program pokusil skočit, je stále na vrchu zásobníku a můžeme si jí přečíst
pomocí příkazu x/gx $rsp (/gx říká, že cheme giant
(64-bitový) integer v hexu). Když získanou adresu předhodíme funkci
cyclic_lookup, nebo opět v příkazové řádce pwn cyclic -l 0x616161706161616f
dostaneme zpět číslo 56, což je přesně ten offset, který jsme hledali.
Tím to ale se schopnostmi pwntools rozhodně nekončí. Jednou z hlavních funkcí je
jednotné rozhraní pro interakci s programem, ať už ho spouštíme jako lokální
proces, připojujeme se na server pomocí TCP nebo třeba přes sériový port. Můžeme
si tak celý exploit zdebugovat lokálně a pak výměnou jednoho řádku provést
exploit na serveru. Knihovna si také umí načíst informace o programu z jeho
binárky a podle těch se pak řídit, nebo spustit automaticky gdb pro
debugging. Nakonec existuje příkaz pwn template, který vygeneruje většinu
exploitu komplet za vás.
Zde je příklad exploitu napsaného pomocí pwntools
Všimněte si, že templatovadlo do exploitu automaticky napsalo informace
o binárce, například to, že není PIE. Funkce flat dostane na vstupu slovník
s offsety a daty, která na ten offset patří, a vrátí bytearray, kde jsou prázdná
místa vyplněna cyclicem. Také automaticky převádí hodnoty do správného
formátu, takže adresu předanou jako prostý int 0x401215 automaticky
převede do správného formátu 64-bitového little-endian ukazatele. Pro získání
adresy samotné se používají symboly načtené z binárky. Funkce interactive připojí vstup a výstup programu přímo k terminálu, takže dojde mimo
jiné k vypsání vlajky.
Podle parametrů příkazové řádky se pak exploit buď připojí na vzdálený server,
nebo spustí binárku lokálně. S parametry LOCAL GDB pak rovnou v novém okně
terminálu otevře gdb.
Úplně poslední doporučení na závěr je plugin pro gdb jménem pwndbg, ale objevování jeho výhod je ponecháno jako cvičení. ;)
 36-5-S Učení bez učitele (Zadání)
36-5-S Učení bez učitele (Zadání)
Úkol 1. (K-means) a 4. (KNN)
Jak jste mohli zjistit, tak naprogramovaní obou algoritmů je přímočaré a vcelku jednoduché. Zde asi není potřeba nic více dodávat.
Vzorové řešení K-means (Python 3)
Bonusový 2. úkol
Tato úloha byla trochu složitější. Sice jste nemuseli nic vymýšlet, ale pro implementaci bylo potřeba pochopit aktuální i minulé díly seriálu. Nicméně, pokud jste se „prokousali“ textem všech dílů a rámcově jste je pochopili, tak věříme, že implementace této úlohy nebyla nemožná.
Vzorové řešení implementace neuronových sítí (Python 3)
3. úkol: Simulace PCA
U tohoto úkolu je nejdříve potřeba pochopit, co v principu dělá PCA, což jste měli napsané přímo v zadání této úlohy. Struktura výsledné neuronové sítě je asi zřejmá. Chceme mít vstupní vrstvu o n neuronech a výstupní vrstvu o m neuronech. Mezi vstupní a výstupní vrstvou můžou být skryté vrstvy, ale není to nutné.
Teď ale přichází kámen úrazu, jak tuto síť natrénujeme. K této úloze byla připsaná i nápověda, že můžeme již natrénovanou síť dál upravovat, např. mazat vrstvy.
Když se nyní zamyslíme, tak známe ztrátovou funkci. Také známe vstupní data, ale neznáme redukovaná vstupní data. Můžeme ovšem udělat trik: při trénovaní naše chtěná výstupní vrstva nebude výstupní vrstva při učení, ale za touto vrstvou bude následovat další vrstva o n neuronech. Poté můžeme vstupní data použít i jako cílový výstup (target).
Síť bude dělat to, že nejdříve data zkomprimuje do dimenze o velikosti m a poté se pokusí co nejpřesněji rekonstruovat původní data (do dimenze o velikosti n) Po natrénování přidanou vrstvu smažeme a máme naši hledanou síť.
Těmto sítím, které se učí jen ze vstupní dat, se říká autoenkodéry a hojně se používají ve strojovém učení. Např. nyní nejvíce používaný typ modelu v oblasti zpracování jazyka – transformer – je vlastně jeden velký autoenkodér.
Soutěžní úloha
U této úlohy jste mohli použít libovolný model z knihovny scikit-learn
a mohli jste si vyzkoušet zjistit, jaký model
je vhodný pro tato data. Zde je důležité poznamenat, že je důležité
brát v potaz i to, jak velký dataset máme. Pokud bychom měli obrovský
dataset, nejspíše by vyhrály neuronové sítě. Náš dataset je ovšem malý,
tak je dobré vyzkoušet i jiné modely.
Dosáhnout přes baseline bylo vcelku jednoduše dosažitelné pomocí rozhodovacích stromů, náhodných lesů, ADA či gradient boosting rozhodovacích stromů.
Jelikož známe docela mnoho modelů, hodí se vyzkoušet některé z nich a zjistit, jak si vedou na daných datech. Vybrané modely jsou: Logistická regrese s L2 regularizací, neuronová síť s dvěma skrytými vrstvami: 100 a 50 neuronů, náhodný les s 2000 stromy, gradient boosting rozhodovací stromy s 2000 stromy a KNN s 3 sousedy. Výsledek je následující:
| Model | Trénovací přesnost | Testovací přes. |
| Logistická regrese | 93.11 % | 92.7 % |
| Neuronová síť | 93.39 % | 92.3 % |
| Náhodný les | 99.97 % | 95.1 % |
| Gradient boosting | 99.97 % | 94.6 % |
| KNN | 90 % | 78.9 % |
Jak můžeme vidět, rozhodovací stromy drtí jak trénovací, tak i testovací přesnost. Dokonce můžeme vidět, že samotná logistická regrese dokáže překonat soutěžní baseline – 92.5 %.
Jak řešení vylepšit? Podle tabulky asi dává největší smysl zaměřit se na stromy. Samozřejmě můžete namítnout, že naše zvolené hyperparametry nemusely být zvolené nejlépe a moc ukvapeně jsme zavrhli nějaký model. Ano, dává smysl udělat nějaký gridsearch hyperparametrů a vyzkoušet feature engineering, ale kromě stromů jsem já osobně nebyl moc úspěšný.
Dobrá, jak vylepšit stromy? Můžeme vyzkoušet nějakou augmentaci dat. Zde si je
potřeba uvědomit, že augmentace, které dělají škálování dat (StandardScaler),
na trénovacích datech nic neudělají (naučený model bude mít stejnou přesnost jako model
bez augmentace). Je to jednoduše způsobené tím, rozhodovací práh se volí podle
průměru 2 hodnot v dané feature a průměru je jedno, jak jsou data naškálovaná.
Tím, ale neříkáme, že bude stejná predikce i na testovacích datech.
Může se stát, že vrchol rozhodovacího stromu u testovacího data bez transformace
půjde jednou např. do levého syna, ale transformovaná data bude predikovat do
pravého syna. Má to ovšem jednu potíž: trénovací přesnost nám nenapoví, jestli
si dokážeme pomoci na testovacích datech.
Já osobně jsem vyzkoušel StandardScaler a RobustScaler a
skončil jsem u druhé transformace, i když není jasné, jestli vůbec pomáhá.
Dále jsem vyzkoušel polynomiální featury do druhého stupně, ale ty snad nepomohly
ani jednomu modelu.
Poté jsem jen udělal veliký gridsearch hyperparametrů pro náhodné lesy a gradient boosting a výsledné modely mají testovací přesnost mezi 95.4 % až 95.9 %. Oproti původním výsledkům jsme si o tolik nepolepšili a zároveň trénovací přesnost je zcela identická, takže jediná možnost, jak zjistit, jestli jsou predikce lepší, bylo využití dynamické výsledkové listiny.
V dynamických výsledkovkách pro 4. a 5. sérii je u nejlepších řešitelů i stručný popis využitých modelů. Není to úplný popis, např. nějaké augmentace se používají jen na určité sloupce, ale tuto informaci neuvádím, jinak by popis byl vcelku dlouhý.
Doufám, že jste si seriál užili. Moc děkuji za pěkná řešení a mějte se fanfárově.
 36-5-X1 Superstring (Zadání)
36-5-X1 Superstring (Zadání)
Nejprve se zamyslíme nad tím, jak zkontrolovat, zda se v nějakém řetězci (seně) vyskytují všechna zadaná slova (jehly).
Pořídíme si vyhledávací automat Aho-Corasicková (viz Kuchařka o hledání v textu, případně kapitola 13.3 v Průvodci labyrintem algoritmů). Automatem pak budeme procházet seno a udržovat si množinu jehel, které jsme už viděli (třeba jako posloupnost nul a jedniček).
Jak dlouho to potrvá? Označme n počet slov, m jejich celkovou délku, s délku sena a a počet znaků abecedy. Konstrukce automatu trvá O(ma), projití sena O(s) plus O(1) na každý nahlášený výskyt, kterých je přinejhorším O(ns).
Seno nicméně neznáme. Vytvoříme si proto graf popisující všechny možné výpočty předchozího algoritmu a najdeme v něm nejkratší úspěšný výpočet.
Konkrétněji: vrcholy grafu budou stavy výpočtu. To jsou uspořádané dvojice (S,M), kde S je stav automatu a M množina nalezených jehel. Pro každý vrchol (S,M) a každý znak Z abecedy sestrojíme hranu, která odpovídá pokračování výpočtu po přečtení znaku Z ze sena – tedy provedení jednoho kroku automatu a rozšíření množiny M o všechny právě nalezené jehly. Tím získáme nový stav a novou množinu, tedy nový vrchol. K vytvořené hraně si zapamatujeme znak Z.
V tomto grafu pak hledáme nejkratší cestu z počátečního vrcholu (počáteční stav,∅) do libovolného vrcholu, jehož množina obsahuje všechny jehly. Znaky na hranách této cesty nám řeknou hledaný „nadřetězec“.
Rozmysleme si časovou složitost. Automat má O(m) stavů, množin jehel existuje 2n. Graf proto má V=O(2n m) vrcholů, z každého vede a hran, takže hran je celkem E=Va=O(2n ma). Spočítat cíl jedné hrany trvá O(m+n), protože jeden krok automatu v nejhorším případě proskáče po zpětných hranách až do kořene (což může být až m hladin) a nahlásí až n výskytů, které přidáme do množiny jehel velké O(n). To vše se dohromady vejde do O(m), takže celý graf sestrojíme v čase O(Em) = O(2n m2 a). V tomto čase stihneme i konstrukci automatu a hledání nejkratší cesty.
Tuto složitost jde ještě trochu zlepšit. Jednak si můžeme pro každý stav automatu S a každý znak Z předpočítat, kam nás zavede jeden krok automatu, a tím se v hlavní části algoritmu vyhnout zpětným hranám. To není nic jiného než převedení vyhledávacího automatu na obyčejný konečný automat. Předvýpočet provedeme po hladinách: z kořene vedou všechny kroky zpět do kořene, na každé další hladině pak znak Z buď má svou dopřednou hranu, nebo z něj automat jde zpětnou hranou do stavu na vyšší hladině, kde už máme předpočteno. To stihneme ve stejném čase O(ma), jaký nás stálo vytvořit automat.
Také můžeme množiny reprezentovat bitovými maskami. Na to potřebujeme předpokládat, že náš počítač pracuje s n-bitovými čísly v konstantním čase, ale to je docela opodstatněný předpoklad u algoritmu s exponenciální složitostí. S bitovými maskami pak běžné množinové operace (přiřazení, průnik, sjednocení, rozdíl, dotaz na přítomnost prvku) běhají v konstantním čase.
Nakonec si můžeme pro každý stav automatu předpočítat množinu nalezených jehel, opět reprezentovanou bitovou maskou. Tento předvýpočet opět provedeme po hladinách v čase lineárním s velikostí automatu.
S těmito třemi triky můžeme cíl jedné hrany nalézt v konstantním čase, takže se konstrukce grafu zrychlí na O(E) = O(2n ma). Do tohoto času se zase vejde jak konstrukce automatu, tak prohledání grafu.