Druhá série třicátého šestého ročníku KSP
Celý leták v PDF.
Dostává se k vám druhé číslo hlavní kategorie 36. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: neděle 17. prosince 2023 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo získá z této série alespoň 42 bodů.
Zadání úloh
- 36-2-1: Fronty na poště
- 36-2-2: Záchrana mravenců
- 36-2-3: Ztracená bunda
- 36-2-4: Nejlepší programovací jazyk, část II.
- 36-2-S: Chození po gradientu
- 36-2-S2: Soutěžní úloha seriálu
 36-2-1 Fronty na poště (10 bodů)
36-2-1 Fronty na poště (10 bodů)
„Jupí!“ Kevinovi právě jeho vlastnoručně vyrobené hodinky oznámily, že mu na poštu dorazila sladká odměna za odevzdání originálního řešení úlohy Nejlepší programovací jazyk z minulé série KSP. Jenže na poště bývají hrozně dlouhé fronty. Komu by se v nich chtělo čekat? Naštěstí si Kevin po hrozivé zkušenosti z minula, kdy strávil čekáním na poště několik hodin, napsal počítačový program (také díky znalostem ze seriálu o strojovém učení). Ten umí předpovídat, kdy lidé chodí na poštu a jak vůbec pracují tamní úředníci. Nyní by ho ale zajímalo, jak z těchto dat vyčíst, kdy má na poštu přijít, aby strávil čekáním ve frontách co nejméně času a vyzvedl si zásilku.

Pošta, a tedy i Kevinův simulátor, fungují následujícím způsobem: Na poště se nachází Q přepážek, za kterými sedí úředníci. Ke každé přepážce je samostatná fronta. Dále se na poště dějí tři druhy událostí:
- Někdo nový přijde na poštu a zařadí se na konec fronty u přepážky číslo 0. (Na té se mimochodem i vystavují lístečky s čísly pro další vyřizování zákazníkovy žádosti.)
- Úředník na přepážce j rozhodne, že s požadavkem prvního zákazníka ve frontě (těžko říct, kdo přesně to bude – možná to může být i Kevin) si neví rady (nebo se mu zrovna nechce moc pracovat), a pošle jej k přepážce číslo k, kde se zákazník zařadí na konec fronty. Číslo k není nikdy 0, protože kdyby někdo měl dva lístečky, mohlo by to rozhodit interní systém pošty.
- Úředník na přepážce j vyřídí žádost prvního zákazníka ve své frontě, a ten poté, pln frustrace z přebujelého byrokratického systému, odchází deprivován domů.
V jednu chvíli pošta zavře. Zbylí zákazníci mají smůlu a už na ně nepřijde řada.
Poradíte Kevinovi, kdy má na poštu přijít, aby strávil čekáním ve frontách co nejméně času a co nejdříve si odnesl zásilku?
Slibujeme, že dvě události nikdy nenastanou ve stejném čase. Kevin však může přijít ve stejnou dobu jako někdo jiný. Protože je ale slušně vychovaný, pustí vždy danou osobu před sebe. Dále slibujeme, že vždy bude aspoň jedna žádost odbavena a nikdy nebude úředník obsluhovat prázdnou frontu.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete dvě celá kladná čísla Q a P. Číslo Q udává počet přepážek, které jsou očíslované od 0 do Q - 1. Číslo P značí počet událostí. Na dalších řádcích dostanete v chronologickém pořadí P událostí. Každá událost je popsána časem t, kdy nastala, a typem y. Typ y je jedním ze tří znaků N, P nebo V:
- N - někdo nový přišel na poštu.
- P - přesun zákazníka. V tom případě ještě dostanete na dalším řádku dvě čísla j a k, o které přepážky se jedná.
- V - něčí žádost byla vyřízena. Na dalším řádku je jedno číslo j, na které přepážce se tak stalo.
Formát výstupu: Na výstup vypište dvě čísla W a C. Číslo C říká, kdy má Kevin na poštu přijít, aby strávil čekáním na poště co nejméně času W. Pokud existuje víc možností, kdy může přijít a čekat W času, pak vypište tu, která začíná nejdříve - Kevin se už totiž nemůže dočkat svých sladkostí.
3 7 2 N 3 P 0 1 5 N 8 N 9 V 1 10 P 0 2 11 V 2
8 4
Kevinovi se vyplatí přijít v čase 4. Protože nikdo nepřijde ve stejný moment, tak se rovnou zařadí do nulté fronty. (Jinak by pustil všechny lidi před sebe a až pak by se zařadil do fronty.) Poté se v čase 10 přesune do druhé fronty. V čase 11 dostane svou sladkou odměnu a jde domů. Na poště tedy strávil čas od 4 do 11, což je 8 jednotek času. Kdyby přišel později, už by se na něj nedostalo.
 36-2-2 Záchrana mravenců (12 bodů)
36-2-2 Záchrana mravenců (12 bodů)
„Pozor! Padá šiška!” zakřičela Sára na Kevina z druhé strany lesní cesty. Kevin v mžiku změřil, kam nahlášená šiška dopadne a ihned se dal do zachraňování nebohých mravenců na cestičce. Na každého mravence, kterého si přál ochránit, položil krabičku od zápalek. Když pak šiška dopadla na zem, místo mravenců zasáhla a poničila jen položené krabičky. Ty ale teď po šišce nejsou znova použitelné, a Kevin tak musí s dalším poplašným výkřikem Sáry pokládat krabičky nové. Ale ouha, na záchranu všech mravenců by Kevin nyní potřeboval 5 krabiček, v kapse mu ale zbývají už jen 2.
Lesní cesta má tvar tabulky N ×N, na níž se na každém políčku buďto vyskytuje nebo nevyskytuje mravenec (mravenci se nehýbou, zůstávají na stále stejném místě). Kevin má jen K krabiček od sirek a s každou z nich dokáže ochránit pouze jednoho mravence od jednoho dopadu šišky.
Před samotným začátkem padání šišek se Sára podívá na borovici nad cestou a přesně určí, kdy a kam budou dopadat jak velké šišky. Dopadová plocha šišky má tvar obdélníku o zadaných rozměrech – může být pro každou šišku jinak velká.
Kevina by zajímalo, kdy a kam má umístit nejvýše K krabiček tak, aby po konci padání S šišek zachránil co nejvíce mravenců.
Pozor, mravenců může být opravdu hodně, nechceme tedy, aby složitost řešení závisela na jejich počtu.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-2-3 Ztracená bunda (13 bodů)
36-2-3 Ztracená bunda (13 bodů)

Jirka si užil týden lyžování v horách, ale nastal čas odjezdu domů. Zabalil si tedy své věci a chystal se vyrazit na nádraží, když zjistil, že někde ztratil svoji bundu. Vlaky mají sice topení, takže v nich by mu bunda nechyběla, ale na nástupištích je strašná zima, a Jirka by nerad nachladl. Chtěl by tedy naplánovat takovou cestu domů, aby strávil v součtu co nejkratší dobu na nástupištích. Pomůžete mu?

Dostanete k dispozici jízdní řády vlaků. Cesta může trvat více dní, vlaky jezdí každý den stejně. Jeden den má 86400 sekund, s letním časem není třeba počítat. Za čas strávený na nástupišti se považuje součet časů na přestupy, neboli rozdílů odjezdů a příjezdů v každé stanici. Navíc se k němu připočítává čas do odjezdu prvního vlaku. Pokud chce Jirka přestoupit do vlaku, který odjíždí v dřívější čas, než ve který Jirka do přestupní stanice přijede, tak tam může počkat do dalšího dne. Jirkovi je jedno, v jaký čas dorazí domů. Žádný vlak nezastavuje ve stejné stanici více než jednou, žádné dva vlaky nezastavují ve stejné stanici ve stejný čas.
 V prvních třech vstupech za celkem 6 bodů se může Jirka dostat domů za dvanáct hodin,
a navíc nejezdí žádné vlaky mezi šesti hodinami večer a šesti hodinami ráno.
V prvních třech vstupech za celkem 6 bodů se může Jirka dostat domů za dvanáct hodin,
a navíc nejezdí žádné vlaky mezi šesti hodinami večer a šesti hodinami ráno.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku bude název stanice, odkud Jirka jede, a čas, kdy tam začíná. Na druhém řádku bude název stanice, u které Jirka bydlí. Na třetím řádku bude počet vlaků v jízdním řádu. Poté budou následovat informace o jednotlivých vlacích. Popis každého vlaku bude začínat jedním řádkem, na kterém bude jeho jméno a počet stanic, ve kterých zastavuje. Poté bude následovat řádek za každou stanici, na kterém bude její jméno a čas, kdy v ní vlak zastavuje.
Jména stanic a vlaků se skládají jen z písmen anglické abecedy,
arabských číslic a spojovníků (-).
Vždy obsahují alespoň jeden znak.
Časy jsou celá čísla, která vyjadřují čas od půlnoci v sekundách.
Formát výstupu: Na výstup vypište všechny využité spoje. Za každý spoj vypište na jeden řádek jméno vlaku, kterým má Jirka jet, a jméno zastávky, na které má vystoupit. Jirka vždy pojede zadaným vlakem co nejdříve to jde, nebude čekat do dalšího dne zbytečně.
RAMZOVA 62100 BRNO-HL-N 4 R1100 4 BOHUMIN 16500 PREROV 20340 BRNO-HL-N 25140 BRNO-KRALOVO-POLE 26040 R914 4 SUMPERK 22260 ZABREH-NA-MORAVE 23400 OLOMOUC-HL-N 25260 BRNO-HL-N 31320 SP1402 4 JESENIK 61260 RAMZOVA 62640 HANUSOVICE 64620 ZABREH-NA-MORAVE 66300 R899 5 PRAHA-HL-N 77460 KOLIN 79620 PARDUBICE 81180 ZABREH-NA-MORAVE 84960 PREROV 780
SP1402 ZABREH-NA-MORAVE R899 PREROV R1100 BRNO-HL-N
Nejlepší plán pro Jirku je počkat 540 sekund na vlak SP1402 a jet do Zábřehu na Moravě, tam počkat 18 660 sekund na vlak R899 do Přerova a tam počkat 19 560 sekund na vlak R1100 do Brna. Celkem tedy Jirka stráví 38 760 sekund čekáním na nástupištích.
Mohl by místo toho jet ze Zábřehu na Moravě do Brna přímo vlakem R914, ale to by strávil čekáním celých 44 040 sekund.
Organizátoři KSP neručí za správnost jízdních řádů v testovacích vstupech.
 36-2-4 Nejlepší programovací jazyk, část II. (10 bodů)
36-2-4 Nejlepší programovací jazyk, část II. (10 bodů)
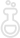
Vážení řešitelé, děkujeme vám za spoustu kreativních a zajímavých instrukcí! Jejich kombinací vznikl vskutku… lahodný programovací jazyk. S radostí tedy oznamujeme, že naše poznatky jsou konzistentní s dosavadním výzkumem [1]. Nyní je čas vyzkoušet náš nový jazyk, říkejme mu ksplang, v praxi, a to na velice zákeřných informatických úlohách, na které byste v běžném programovacím jazyce určitě jen těžko hledali řešení na víc než tři řádky.
Kompletní seznam instrukcí ksplangu naleznete na samostatné stránce. Na stejném místě taktéž naleznete odkaz na interpreter jazyka, který můžete použít pro ladění vašich programů.
Pro připomenutí, jazyk počítá s 64-bitovými celými čísly se znaménkem. Přetečení čísla při výpočtu způsobí ukončení programu chybou. Jediná paměť, kterou má program k dispozici, je zásobník. Ten si můžete představit jako posloupnost čísel uspořádanou shora dolů. Nová čísla přidáváme na vrchol zásobníku, odebíráme opět z vrcholu. Zásobník má omezený počet prvků (v této úloze 2 097 152) a jeho překročení ukončí program chybou. Ve všech úkolech můžete předpokládat, že se na zásobník vejde aspoň dalších 1000 čísel. Pro účely vyhodnocení úlohy je čas výpočtu též limitován, nicméně všechny zadané úkoly se do limitu hravě vejdou.
Program je sekvencí instrukcí v textové formě oddělených libovolnými whitespace znaky (mezerami, novými řádky, …). Sekvence obsahuje pouze instrukce, není možné do sekvence zadat konstanty. Instrukce nemají žádné parametry, pracují pouze se zásobníkem. Pokud na zásobníku není dostatek hodnot pro vykonání instrukce, program bude ukončen chybou. Počáteční stav zásobníku bude pro každou úlohu definován.
„Vstupem“ programu se rozumí stav zásobníku před jeho spuštěním a „výstupem“ stav po jeho ukončení.
Příklad: program ++ ++ max zvýší číslo na vrcholu zásobníku o 2,
a poté nahradí horní dvě čísla na zásobníku tím větším z nich.
Pokud by na zásobníku byly méně než dvě hodnoty, program by skončil chybou.
Tuto úlohu odevzdávejte v odevzdávátku, podobně jako běžné opendata úlohy. Generované vstupy můžete v odevzdávátku ignorovat, vaše ksplangové programy odevzdávejte v textové podobě jakožto výstup k danému úkolu. Po odevzdání je náš interpreter ksplangu spustí na několika neveřejných testovacích vstupech a dá vám vědět o výsledku.
Úkol 1 – Nula [3b]
Přidejte na zásobník číslo 0. Zásobník na vstupu není prázdný, vždy je na něm alespoň jedno číslo. Výstupem programu je tedy celý jeho původní vstup, a navíc jedna nula na vrchu zásobníku.
Úkol 2 – Negace [2b]
Znegujte číslo na vrchu zásobníku. Na zásobníku je alespoň jedno číslo. Negované číslo nahraďte, ale cokoli před ním neměňte. Například číslo 42 nahraďte za -42 či naopak. Váš program by měl fungovat na celém rozsahu 64-bitových celých znaménkových čísel, kromě jeho nejmenší možné hodnoty (ta nemá v 64 bitech kladný ekvivalent).
Úkol 3 – Duplikace [5b]
Máte neprázdný zásobník, zduplikujte číslo na vrcholu. Můžete předpokládat, že toto číslo je rozumně malé, vešlo by se i do 32-bitového integeru, tedy je v rozsahu -2147483648 až 2147483647. Výstupem programu je tedy celý jeho původní vstup, a navíc kopie vrchního čísla na vrchu zásobníku.
Zdroje
[1] ČAPEK, Josef. Povídání o pejskovi a kočičce. 16. vyd., Praha: Albatros, 2003. 118 s. Strana 79.

 36-2-S Chození po gradientu (12 bodů)
36-2-S Chození po gradientu (12 bodů)
Právě čtete druhý díl seriálu. Pokud jste neřešili ten první, pro pochopení následujících odstavců je vhodné si jej přinejmenším přečíst. Úlohy z něj je stále možné odevzdávat za polovinu bodů.
V minulém díle jsme si představili lineární regresi, ale neukázali jsme si, jak ji natrénovat. Ti, kdo udělali bonusový úkol, tak znají jednu možnost učení lineární regrese – zjistili vzorec na vypočítání optimálních vah vůči daným datům. Představený model (lineární regrese) je vcelku dost jednoduchý, protože jak je výstup lineární vůči vstupu, tak se optimální váhy dají vypočítat přesně, což je luxus, který u složitějších modelů nemáme. Proto se podíváme na jinou možnost na trénování modelů, která se v praxi používá na trénování složitějších modelů a pomocí ní si natrénujeme i naši lineární regresi. Budeme učit náš model pomocí gradientu!
Gradient
Co je to gradient? Gradient je soubor parciálních derivací podle všech proměnných. Tedy např. když jsme v minulém díle derivovali funkci MSE podle vah, tak gradient je
| ∂MSE |
| ∂w1 |
| ∂MSE |
| ∂w2 |
| ∂MSE |
| ∂wf+1 |
Opravdu si to představte jako pole, kde v každém políčku je uložená jedna parciální derivace. V lineární algebře se tomuto „poli“ říká vektor. Jediný velký rozdíl je v tom, že pole byste si představovali jako jeden dlouhý řádek čísel, ale vektor je dlouhý sloupec čísel.
Už víme, co je to gradient, ale co nám říká? K zodpovězení této otázky se vrátíme zpět k parciálním derivacím. Parciální derivace nám říkají, jak moc se funkce změní, když trochu změníme jednu proměnnou. Pokud je parciální derivace v daném bodě kladná, tak se funkce zvětší, když miniaturně zvětšíme danou proměnnou. Naopak pokud je záporná, tak se funkce zmenší.
Můžeme si to představit tak, že každá parciální derivace je jedna „směrovka“, která ukazuje, jak moc a jakým směrem funkce nejvíce roste, když změníme právě jeden konkrétní parametr funkce. Gradient tyto směrovky složí do jedné šipky, která ukazuje, jakým směrem funkce nejvíce roste.
Ukažme si příklad gradientu funkce o dvou proměnných. Vektor (3, 0) představuje parciální derivaci podle prvního parametru. Předtím jsme brali parciální derivaci jen jako číslo, ale nyní pro geometrickou reprezentaci směrovky potřebujeme vektor, kde i-tá parciální derivace je uložena na i-té pozici a všude jinde jsou nuly. Vektor (0, 1) představuje parciální derivaci podle druhého parametru. Gradient je poté červený vektor (3, 1) neboli gradient je složení vektorů. Na obrázku máte příklad znázorněn.

Gradient je tedy vektor parciálních derivací a říká nám, jakým směrem funkce nejvíce roste.
Nám by se ovšem hodila informace, jakým směrem funkce nejvíce klesá. To se ale jednoduše zjistí z gradientu – před gradient dáme minus. Minus gradient nám naopak říká, jakým směrem funkce nejvíce klesá.
Gradient descent
Nyní si zkusíme vymyslet jednoduchý algoritmus, který bude hledat minimum funkce. Stojíme v nějakém bodě a chceme se dostat do bodu, kde je funkční hodnota minimální. Jak toho dosáhnout? Podíváme se směrem, kterým funkce nejvíce roste, a uděláme krok vzad. Tedy se posuneme ve směru minus gradient. Tento postup budeme opakovat, dokud se nedostaneme do minima.
Nyní je otázka jak velký krok máme udělat. Pokud budeme dělat moc velké kroky, tak se může stát, že minimum vždy přestřelíme a nikdy se do něj nedostaneme. Pokud budeme dělat moc malé kroky, tak nám bude dlouho trvat, než se dostaneme do minima. Proto si zvolíme nějakou konstantu α, která bude říkat, jak velký krok budeme dělat. Této konstantě α se říká learning rate a tato konstanta bude náš první hyperparametr. Hyperparametr znamená, že tento parametr si model nenastavuje sám, ale nastavujeme ho my na začátku učení. Náš algoritmus bude vypadat následovně:
kde w je vektor vah, α je learning rate a ∇w E(w) je gradient ztrátové funkce E(w) vůči vektoru vah w. Funkce E se rovná průměru hodnot z nějaké ztrátové (loss) funkce na jednotlivých datech. Pro lineární regresi je MSE (což je průměr kvadratických chyb) hledaná funkce E a její parciální derivace známe z minulého dílu.
Dále nebojme se toho, že tady najednou používáme vektor vah w, tento postup funguje i tak, že si postupně vypočítáme jednotlivé parciální derivace a upravujeme váhy podle nich. Tady si jen potřebujeme dát pozor, že když vypočítáme parciální derivaci podle váhy w1, tak tuto váhu nemůžeme hned nahradit starou vahou! Všechny parciální derivace musíme vypočítat se starými vahami a až poté je nahradit novými váhami. Tedy učení bude vypadat nějak takto:
w'1 ←w1 - α·
| ||
| ⋮ | ||
w'f ←wf - α·
| ||
| w ←w' |
Tomuto algoritmu na hledání minima se nazývá gradient descent.
 Trochu jsme vám kecali. Funkce E se ve skutečnosti počítá jako střední
hodnota z nějaké ztrátové funkce na jednotlivých datech.
Pokud bereme, že všechna data z datasetu jsou stejně pravděpodobná, tak střední hodnota
je opravdu rovna klasickému průměru. Jinak je střední hodnota rovna váženému
průměru.
Trochu jsme vám kecali. Funkce E se ve skutečnosti počítá jako střední
hodnota z nějaké ztrátové funkce na jednotlivých datech.
Pokud bereme, že všechna data z datasetu jsou stejně pravděpodobná, tak střední hodnota
je opravdu rovna klasickému průměru. Jinak je střední hodnota rovna váženému
průměru.
Standardně data z datasetů bereme stejně pravděpodobná, ale občas se vyplatí data „převáhovat“. Představte si, že máte klasifikovat data, jestli na obrázku je kočka nebo pes. V testovací množině jsou tyto data v nějakém poměru, ale pokud máme podezření, že tento poměr je v testovacích datech jiný, tak dává smysl převáhovat data z trénovacího datasetu, aby více odpovídal poměru v testovacích datech.
Varianty gradient descentu
První varianta je (Standard/Batch) Gradient Descent. Ta funguje tak, že vezmeme všechna data, spočítáme gradient, upravíme váhy a toto budeme opakovat. Zde je výhoda, že gradient máme přesně vypočítaný – počítáme střední hodnotu gradientů přes všechna data. Nevýhoda ale je, že pokud máme hodně příkladů, jedna úprava vah může být hodně pomalá. Hlavně pokud si představíme dataset s několika miliony obrázků, tak výpočet gradientu bude hodně pomalý.
Dobrá, tak zkusme jiný přístup, který se nazývá Stochastic Gradient Descent (SGD). Zde vezmeme náhodně jen jedno dato a podle něj upravíme váhy. U tohoto postupu jsou úpravy vah rychlé, ale bude nám tento postup fungovat a najde minimum? Zde je důležité, že bereme data náhodně. Kdybychom je nebrali náhodně, ale pokaždé procházeli data ve stejném pořadí, tak budeme dělat systematickou chybu a nemusíme se dostat do minima. Když však budeme brát data náhodně a budeme toto opakovat dostatečně dlouho, tak v průměru se tato hodnota bude přibližně rovnat střední hodnotě ztrátové funkce přes všechna data.
Ale nemusíme být tak extrémní a můžeme zvolit zlatou střední cestu. Můžeme vzít B náhodně vybraných dat. B náhodně vybraných dat se nazývá minibatch a z toho plyne i název tohoto algoritmu – Minibatch SGD. Vypočítáme gradient minibatche, tedy spočítáme aritmetický průměr hodnot ztrátové funkce přes jednotlivá data a nakonec upravíme váhy. Výpočet gradientu pro jeden minibatch bude vypadat následovně:
| B |
| i=1 |
| 1 |
| |B| |
Zde se může jevit nevýhoda, že budeme muset nastavovat další hyperparametr B. Zde se ale nemusíme se bát, protože tento hyperparametr je spíše technický a neovlivňuje moc výsledky. Typicky se nastavuje, aby váhy modelu a samotná minibatch se vešla do RAMky či GPU paměti.
V praxi se vybírání minibatchů dělá tak, že se data z datasetu zamíchají a pak se postupně berou data po B kusech. Tedy první minibatch bude obsahovat prvních B dat, druhý minibatch bude obsahovat dalších B dat atd. Poslední minibatch může být menší než B. Průchodu všemi daty se říká epocha. Po každé epoše se data zamíchají a začne se nová epocha.
Přeučení
Dřív nebo později přijdeme na jeden nepříjemný problém. Když se snažíme co nejvíce snížit trénovací chybu, tak chvíli testovací chyba klesá také, ale poté zase roste. Tomuto jevu se říká přeučení (overfitting) a tento problém se může vyskytnout u všech modelů strojového učení. Ilustrujme si problém na jednoduchém datasetu, kde každé dato má jednu featuru x a výstupní hodnotu.
Když budeme učit lineární regresi na této jedné featuře, tak nám model bude předpovídat jen přímku (víc daný model nedokáže namodelovat). Když do daného modelu přidáme novou featuru x2, tak nám model bude předpovídat kvadratickou křivku. Všimněte si, že lineární regrese je slabý model. Lineární regrese násobí vstupní featury nějakou konstantní váhou a sám si nedokáže vytvořit featuru x2, tuto featuru mu musíme dodat my. Tím, že mu dodáme novou featuru, tak se model stane silnějším – dokáže modelovat více funkcí. No ale pokud budeme s touto myšlenkou pokračovat dál, tak začneme přidávat další featury x3, x4, …, xn-1, kde n je počet dat. Tímto jsme modelu dali tolik volnosti, že dokáže přesně namodelovat data z trénovacího datasetu. Ale opravdu jsme toto chtěli?
Na následujících obrázcích modré body znázorňují trénovací data. Snažíme se natrénovat model, který bude co nejvíce podobný zelené křivce (funkce sinus). Popisek N říká, jaký polynom nejvyššího stupně jsme dodali lineární regresi. Např. pro n=3 model má featury 1 (bias), x, x2 a x3. Černá křivka znázorňuje naší natrénovanou funkci pomocí našeho modelu.
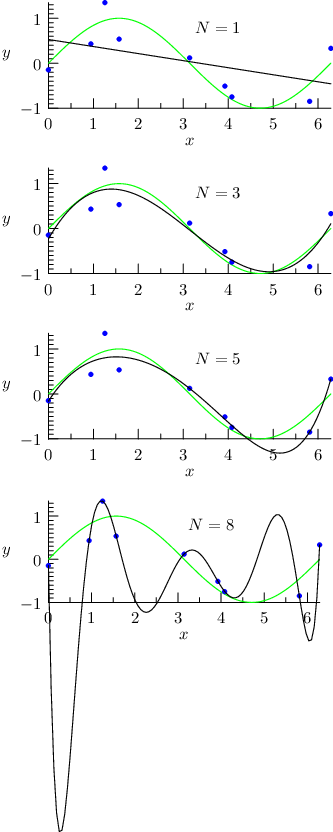
Pokud přidáme x, x2, x3, …, xn-1 feature, tak daný model dokáže přesně namodelovat danou funkci z n bodů. Ano dokázali jsme dostat nulovou chybu na trénovací množině, ale generalizační vlastnost tohoto modelu je příšerná, už dokonce model, který modeluje jen přímku si vede lépe než tento model.
Vyřešit problém přeučení můžeme dvěma způsoby. První možnost je, že odebereme nějaké featury a tím model zeslabíme. Neboli už nebude moct modelovat tolik funkcí. Tomuto omezení říkáme, že snižujeme kapacitu modelu.
Druhá možnost je přidat regularizaci. Regularizace bude nějak omezovat model, aby si nemohl jen „zapamatovat“ data z trénovacího datasetu.
Poznámka: Přeučení dost často souvisí s tím, že máme málo dat. Pokud bychom měli více dat, tak by se model nemohl tak snadno přeučit. Samozřejmě pokud s větším datasetem přidáme i více featur, tak model znovu přeučíme.
Regularizace
Jedna z nejstarších regularizačních technik je vynucování malých vah v modelu. Tato technika funguje na principu „Occamovy břitvy“, která říká, že pokud máme více hypotéz, které vysvětlují data stejně dobře, tak bychom měli použít tu nejjednodušší hypotézu. Prakticky tento princip aplikujeme tak, že preferujeme model s menšími váhami, ale nezakazujeme velké váhy, pokud jsou potřeba.
Konkrétně použijeme L2 regularizaci, která spočívá v tom, že ke ztrátové funkci přičítáme součet druhých mocnin vah, ze kterých počítáme gradient. Derivaci součtu můžeme počítat jako součet derivací (viz pravidla derivací z prvního dílu) a následně vypočítat gradient L2 regularizace. Gradient není složitý na vypočítání a my rovnou prozradíme, že výsledek je 2w (můžete si ověřit, že toto platí). Výsledná aktualizace bude vypadat následovně:
kde α je learning rate a λ je nový hyperparametr, který říká, jak moc má být regularizace silná. Tedy jak moc budeme preferovat menší váhy. Např. pokud bychom měli λ= 0, tak tímto jsme regularizaci vypnuli. Lineární regrese s L2 regularizací se nazývá Ridge Regression.
Občas se můžete setkat s L1 regularizací, která funguje podobně, jen se odčítá součet absolutních hodnot vah. Tato regularizace se nazývá Lasso Regression.
Pokud jste udělali bonusový úkol z minulého dílu, tak tam jste dělali inverzi matice, ale inverze této matice nemusí obecně existovat! Naštěstí, pokud použijeme L2 regularizaci, tak inverze matice vždy existuje (pokud je λ > 0).
Poznámka: Správně bychom neměli regularizovat bias, protože bias se nedá přeučit (určuje posunutí křivky) a bias klidně může nabývat obřích velikostí. Např. když budeme předpovídat cenu nemovitostí, tak tyto ceny budou začínat na několika milionech, tak bias dává smysl mít v řádu 106. My pro jednoduchost budeme implementovat regularizaci, kde budeme regularizovat i bias.
Úkol 1 – Minibatch SGD s [9b]
Naprogramujte minibatch SGD s L2 regularizací. Za implementaci minibatch SGD bez regularizace dostanete 7 bodů, pokud naimplementuje i L2 regularizaci, tak dostanete další 2 body. Pro lehčí implementaci jsme připravili šablonu, která načítá různé parametry jako je learning rate, počet epoch, velikost minibatche, sílu regularizace a další. Vaším úkolem je naimplementovat minibatch SGD, podle popisu výše. Komentáře v šabloně vám pomohou s implementací a pokud vám říká, že danou funkcionalitu máte naimplementovat specifickým způsobem, tak to prosím dodržte. Většinou je to kvůli tomu, aby výsledky byly deterministické.
Ukázky použití (výstupy byste měli mít stejné):
python sgd_sol.py --epoch=4
Epoch 1: train = 103.31421434, test = 117.86563103
Epoch 2: train = 77.40719787, test = 108.20876719
Epoch 3: train = 60.35241020, test = 102.61281589
Epoch 4: train = 48.84099080, test = 99.14106920
Sklearn RMSE = 90.80722977
python sgd_sol.py --batch_size=25 --epoch=4
Epoch 1: train = 126.64024620, test = 126.71501308
Epoch 2: train = 112.17614236, test = 120.84637896
Epoch 3: train = 99.95421640, test = 116.11829531
Epoch 4: train = 89.46774700, test = 112.30490246
Sklearn RMSE = 90.80722977
Všimněte si, že když zvětšíme batch_size parametr, tak to má
za následek, že provedeme méně úprav vah, což má za následek,
že se model pomaleji učí.
python sgd_sol.py --epoch=4 --l2=0.1
Epoch 1: train = 103.48492886, test = 117.94782460
Epoch 2: train = 77.97279997, test = 108.41465282
Epoch 3: train = 61.25676694, test = 102.91563331
Epoch 4: train = 50.02640936, test = 99.50932724
Sklearn RMSE = 90.79129494
Feature engineering
Nyní si vyzkoušíme vytváření nebo úpravu featur z datasetu. V datasetu máme
informace, které jsme opravdu naměřili či zjistili, ale tyto featury nemusí
být přímo vhodné pro náš model. Uvažme dataset realitního makléře
z minulého dílu seriálu a přidali bychom další featuru, která by říkala v jakém
dni v týdnu byl dům prodán. Tato featura by měla hodnotu 1 pro pondělí, 2 pro úterý
atd. V lineární regresi by toto ohodnocení způsobilo, že sobota je dvakrát
lepší (či horší) než středa, protože sobota má hodnotu 6 a středa má hodnotu 3.
Což někdy může být pravda, ale spíše je to nesmysl. Proto by bylo dobré tuto
featuru nějak zakódovat, aby každý den v týdnu měl stejnou váhu. Toho můžeme
docílit tak, že si vytvoříme 7 featur (pro každý den v týdnu jednu) a nastavíme
hodnotu 1 pro daný den a 0 pro ostatní dny. Tímto jsme docílili toho, že každý
den v týdnu má stejnou váhu a model si sám rozhodne, jaké váhy přidělí jednotlivým
dnům. Tomuto kódování se říká one-hot encoding a takto pojmenovaný ho
najdete i v knihovně scikit-learn. OneHotEncoderu můžete předat
možné kategorie, nebo si je může automaticky zjistit ze vstupních dat.
Pozor: OneHotEncoder (a všechny ostatní transformátory dat) se učí na trénovacích
datech, takže pokud se nějaká kategorie nevyskytuje v trénovacích datech,
tak ji encoder nezná a OneHotEncoder buď na zakódování tohoto data
spadne nebo ji zakóduje jako vektor nul.
Dále občas nějaké featury jsou mnohem větší než ostatní. Např. když jedna featura je obsah v centimetrech čtverečních, která může nabývat obřích hodnot, a druhá featura je počet pokojů, který bývá v řádu jednotek, tak první featura bude mít implicitně mnohem větší sílu než druhá featura (před tím, než featury vynásobíme váhou).
Může se zdát, že není problém, jak velké vstupní hodnoty featur máme, když použijeme explicitní vzorec na vypočítání optimálních vah lineární regrese bez L2 regularizace. A ono je to opravdu pravda, protože tomu vzorci je to celkem jedno. Naproti tomu SGD docela trpí, když hodnoty nejsou přeškálované. Pocit přeškálování u prvního druhu učení pocítíte, pokud použijete L2 regularizaci nebo např. použití polynomiálních featur s jinými transformery dat (např. one-hot encoder).
Tento problém můžeme vyřešit tak, že dané featury přeškálujeme. Například můžeme použít StandardScaler, který vstupní hodnoty přeškáluje tak, aby měly střední hodnotu 0 a rozptyl 1. Tedy všechny hodnoty budou v intervalu [-1, 1]. Znovu opakuji, transformátory se nastavují na trénovacích datech, takže nějaká featura v testovacích datech může být i mimo rozsah [-1, 1], protože daná featura byla ještě menší či větší než cokoliv, co jsme viděli v trénovacích datech.
Existuje o mnoho více přeškálování, ale na ty se podívejte do dokumentace knihovny
scikit-learn.
Upravovat jednotlivé featury selektivně je celkem otravné, proto scikit-learn
nabízí ColumnTransformer, který umí aplikovat různé transformace na
různé featury. Např. můžete říct, že na první featuru se aplikuje
OneHotEncoder, a na všechny ostatní se nic neaplikuje.
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
data = [
['pondělí', 1, 2, 3],
['úterý', 4, 5, 6],
['středa', 7, 8, 9],
['čtvrtek', 10, 11, 12],
['pátek', 13, 14, 15],
['sobota', 16, 17, 18],
['neděle', 19, 20, 21],
]
ct = ColumnTransformer([
# název transformace, transformace, sloupce
('onehot', OneHotEncoder(), [0]),
('passthrough', 'passthrough', [1, 2, 3]),
])
# natrénujeme transformery na trénovací datech
ct.fit(data)
# ukázka jak vypadají transformovaná data
print(ct.transform(data))
Dalším užitečným transformátorem je PolynomialFeatures, který
vytvoří všechny možné kombinace featur až do daného stupně. Např. pokud
máme featury x, y a chceme vytvořit všechny možné kombinace do stupně 2,
tak vytvoříme featury 1 (bias), x, y, x2, xy, y2. Jelikož víme, že lineární regrese
si tyto featury nedokáže vytvořit sama, tak jí je musíme dodat my.
Poslední věc, kterou si ukážeme, je Pipeline. Pipeline je
objekt, do kterého dáme transformátory a model a Pipeline se postará
o to, že když zavoláme fit, tak se nejprve zavolá fit na všech
transformátorech a poté se zavolá fit na modelu. Stejně tak když
zavoláme predict, tak se nejprve zavolá transform na všech
transformátorech a poté se zavolá predict na modelu.
import sklearn.datasets
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
diabetes = sklearn.datasets.load_diabetes()
model = Pipeline([
('poly', PolynomialFeatures(2)),
('reg', LinearRegression()),
])
# natrénujeme celou "pipelinu" transformerů s~modelem
model.fit(diabetes.data[:-1], diabetes.target[:-1])
# natrénovanou "pipelinu" můžeme poté rovnou použít
# na predikci nových dat
prediction = model.predict(diabetes.data[-1:])
Může se nyní zdát, že je strašně otravné psát ke každé transformaci
její název. Tyto názvy se hodí později, pokud pipelinu chceme natrénovat
několikrát s různými hyperparametry a nastavování těchto hyperparametrů
se dělá právě pomocí těchto názvů.
Existuje metoda make_pipeline, která nám vytvoří objekt
Pipeline a kde nemusíme dávat názvy transformací a modelu.
from sklearn.pipeline import make_pipeline
model = make_pipeline(
PolynomialFeatures(2),
LinearRegression(),
)
Úkol 2 – Feature engineering [3b]
V tomto úkolu si vyzkoušíte vylepšení, tvorbu a úpravu featur.
Program bude fungovat tak, že pomocí command-line argumentů předáte,
na jakých featurách se má aplikovat určený transformátor.
Úkolem je vyřešit všechna TODO: v naší šabloně.
Ukázky použití:
python feature_engineering.py --polynomial_features=1
Original data:
0.0453 -0.0446 -0.0062 -0.0160 0.1250 0.1252 0.0192 0.0343 0.0324 -0.0052
0.0926 -0.0446 0.0369 0.0219 -0.0250 -0.0167 0.0008 -0.0395 -0.0225 -0.0218
Transformed data:
0.0453 -0.0446 -0.0062 -0.0160 0.1250 0.1252 0.0192 0.0343 0.0324 -0.0052
0.0926 -0.0446 0.0369 0.0219 -0.0250 -0.0167 0.0008 -0.0395 -0.0225 -0.0218
Teď se podíváme na ukázku aplikace standard scaleru na druhou, třetí a devátou featuru (indexujeme od nuly).
Pozor na to, že pořadí featur na výstupu se liší od pořadí na vstupu!
python feature_engineering.py --polynomial_features=1 --standard_scaler=1,2,8
Original data:
0.0453 -0.0446 -0.0062 -0.0160 0.1250 0.1252 0.0192 0.0343 0.0324 -0.0052
0.0926 -0.0446 0.0369 0.0219 -0.0250 -0.0167 0.0008 -0.0395 -0.0225 -0.0218
Transformed data:
-0.9514 -0.1869 0.6760 0.0453 -0.0160 0.1250 0.1252 0.0192 0.0343 -0.0052
-0.9514 0.7150 -0.4683 0.0926 0.0219 -0.0250 -0.0167 0.0008 -0.0395 -0.0218
Křížová validace
Zatím jsme v prvním dílu seriálu dělali to, že jsme na začátku programu jednou rozdělili dataset na trénovací a testovací množinu, natrénovali jsme se na trénovacích datech, vytvořili predikce z testovacích dat a nakonec jsme si spočítali MSE na testovací množině. Nemuseli jsme nic řešit, protože s našimi vědomostmi z minulého dílu jsme při trénování nemohli nic udělat jinak. Nyní ale upravujeme či vytváříme featury a máme různé volby pro hyperparametry.
Přichází tedy problém, jak se máme rozhodnout, jestli daný model je dobrý? Typicky nemáme výstupní hodnoty pro testovací dataset, tedy se nemůžeme podívat, kde daný model chybuje a rozhodovat se podle testovacího datasetu, jestli použít tyto či jiné volby hyperparametrů. A i kdybychom je měli, tak je to špatné dělat, protože jistým způsobem tímto přístupem děláme overfitting na testovací množině.
Rozhodovat volby hyperparametrů na testovací množině bychom neměli dělat, ale co jiného můžeme dělat? Můžeme si vytvořit validační množinu, kterou vytváříme tak, že odebereme část trénovacích dat z trénovací množiny. Poté se natrénujeme na nových menších trénovacích datech a pro validaci, jak si vedeme, použijeme validační množinu. V angličtině se validační množině říká buď validation set nebo dev set.
Mohlo by se zdát, že máme vyřešeno a všechno je krásně růžové, ale tímto způsobem jsme si mohli přivodit další problém. Když si vytvoříme jednou na začátku programu validační množinu, tak se může stát, že začneme overfittovat na validační množině. Může se stát, že konkrétní rozdělení datasetu bylo moc dobré či špatné a realita vypadá úplně jinak.
Křížová validace (cross-validation) je technika, která nám pomůže lépe odhadnout, jak se náš model bude chovat na neviděných datech. Spočívá v tom, že rozdělíme dataset na k částí a k-krát natrénujeme model na k-1 částech a otestujeme na té poslední části. V prvním trénovaní trénujeme bez první části, v druhém trénujeme bez druhé části atd. Tato nejjednodušší varianta se nazývá k-fold cross-validation.
Samozřejmě si můžete říct, že čím větší bude k, tak tím budeme mít lepší
odhad. Speciálně pro k = n, které se říká leave-one-out cross-validation
kde n je počet dat, tak můžeme dostat nejlepší odhad,
protože při jednom trénovaní nevidíme jen jedno dato.
Samozřejmě čím větší je k, tak tím pomalejší bude celkové trénování,
protože budeme muset natrénovat hodně modelů. Naštěstí lineární regresi
dokážeme natrénovat rychle pomocí explicitního vzorce a ještě dokážeme
dělat díky matematice kouzla, která dokážou tuto validaci spočítat rychle.
Tedy zpomalení trénovaní nebude k-krát, ale jen něco jako dvakrát pomalejší.
Knihovna scikit-learn má implementovanou tuto lineární regresi s křížovou
validací.
Implementovaný model se nazývá RidgeCV a nedělá jen křížovou
validaci, ale dokáže najít nejlepší hodnotu hyperparametru λ.
Jak implementovaný model funguje? Udělá křížovou validaci pro různé
hodnoty λ a vybere nejlepší model na dané metrice (MSE).
Po trénovaní se RidgeCV chová jako klasický Ridge model, který je
natrénovaný na celém datasetu s nejlepší nalezenou hodnotou λ.
RidgeCV má spoustu parametrů, takže je dobré si projít dokumentaci
a podívat, co všechno se dá nastavit.
from sklearn.linear_model import RidgeCV
X, y = diabetes.data, diabetes.target
# chceme najít nejlepší lambda z~tohoto seznamu
clf = RidgeCV(alphas=[1e-3, 1e-2, 1e-1, 1])
# natrénujeme model
clf.fit(X, y)
print(f"Best hyperparameters: {clf.alpha_}")
# natrénovaný model můžeme rovnou použít na predikci
print(f"Prediction: {clf.predict(X)}")
Existuje spoustu dalších variant křížové validace, které se hodí pro různé úlohy. Např. stratified k-fold cross-validation se hodí pro klasifikační úlohy, kde se snaží zachovat poměr jednotlivých tříd v jednotlivých částech (foldech).
Úkol 3 – Soutěž (odevzdává se jako 36-2-S2) [3b]
Nyní nadešel čas na soutěž, kde si vyzkoušíte natrénovat co nejlepší model založený na lineární regresi. Z technických důvodů je soutěž zadaná jako samostatná open-datová úloha 36-2-S2, kterou najdete níže. Zdrojový kód soutěžního programu ale přidejte do ZIPu s řešením seriálu.
Všechny úlohy z tohoto seriálu odevzdávejte dohromady v jednom zazipovaném archivu. Termín odevzdání je 14. ledna ve 32:00 (tedy další ráno v 8:00). Poté lze odevzdávat za snížený počet bodů až do konce ročníku.
Užívejte předvánoční čas a v příštím díle se podíváme na úlohu klasifikace!
 36-2-S2 Soutěžní úloha seriálu (3 body)
36-2-S2 Soutěžní úloha seriálu (3 body)
Z technických důvodů je 3. úkol seriálu oddělenou úlohou. Odevzdává se jako open-datová úloha 36-2-S2, ale prosíme přiložte do zazipovaného archivu k seriálu i svá řešení tohoto úkolu. Pokud to neuděláte, můžeme vám dodatečně body odebrat.
V této soutěži je povolené používat jen model lineární regrese, je zakázáno používat jiné modely implementované v knihovně scikit-learn jako rozhodovací stromy, MLP, …
Jak soutěž bude probíhat? Od nás dostanete trénovací a testovací data. Dále od nás dostanete šablonu, která si v případě potřeby data stáhne a načte vám data. U trénovacích dat budete mít k dispozici vstupní featury a výstupní hodnoty, ale u testovacích dat budete mít k dispozici jen vstupní featury. Vaším úkolem je natrénovat model na trénovacích datech a predikovat výstupní hodnoty pro testovací data. Dataset můžete různě transformovat (augmentovat), ale nesmíte si přidávat další externí data do trénovacího datasetu. Všechny výstupy musí být generované vaším programem. Toto pravidlo nezakazuje mít v programu pravidla, která výstupy upravují. Tyto predikce poté odevzdáte do odevzdávátka.
Vaším úkolem je vypredikovat počet půjčených kol na základě vstupních dat. Více o datasetu a o vstupních featurách se dozvíte v šabloně.
Pokud vaše řešení bude splňovat, že chyba na testovacích datech bude maximálně 350 (této hodnotě budeme říkat práh) na RMSE metrice, tak dostanete 3 body. Tím ale zábava teprve začíná, protože tímto krokem jste se kvalifikovali do soutěže.
V soutěži budete soutěžit s ostatními řešiteli až o další 3 bonusové body. Abyste věděli, jak si stojíte, tak k této úloze je i dynamická výsledkovka. Na této výsledkovce uvidíte svou RMSE metriku na testovacích datech nebo hodnotu prahu, podle toho, jaká hodnota je horší. Dále na této výsledkovce budete řazeni podle RMSE metriky na testovacích datech. Pokud jste v soutěži, tak sice neuvidíte RMSE metriku, ale pořád budete vědět, kolik lidí je lepší než vy.
Bonusové body se budou udělovat podle následujícího kritéria: Nejlepší první čtvrtina řešitelů řazená podle RMSE metriky, která se kvalifikovala do soutěže, dostane 3 body, druhá čtvrtina dostane 2 body a třetí čtvrtina dostane 1 bod. Bonusové body budou přiděleny po prvním deadlinu pro tento díl seriálu.
Hodně štěstí!