Čtvrtá série třicátého šestého ročníku KSP
Celý leták v PDF.
Dostává se k vám čtvrté číslo hlavní kategorie 36. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: neděle 7. dubna 2024 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo z každé úlohy série získá alespoň 2 body.
Zadání úloh
- 36-4-1: Oprava vzducholodi
- 36-4-2: Megasněhulák
- 36-4-3: Sklad s bednami
- 36-4-4: Heslo
- 36-4-S: Nechme stromy růst
- 36-4-S2: Soutěžní úloha seriálu
- 36-4-X1: Počet koček
 36-4-1 Oprava vzducholodi (10 bodů)
36-4-1 Oprava vzducholodi (10 bodů)
Kevin ve svém povánočním úklidu pokoje naprosto selhal a usoudil, že bude nejlepší se nadobro přestěhovat. Nájmy však nejsou v dnešní době zrovna nejlevnější, a tak se Kevin po uvážení různých alternativ rozhodl usídlit v oblacích.
Pořídil si za tímto účelem prastarou vzducholoď, která je aktuálně ve velmi špatném technickém stavu. Kevina tak čeká před prvním vzletem spousta práce – bude muset provést rozsáhlé opravy, sehnat dostatek paliva, podplatit místní úřady…
Aby se Kevin ve svých četných povinnostech vyznal, vytvořil seznam N úkolů a u každého z nich si poznamenal předpokládanou dobu potřebnou k jeho provedení. Platí, že některé úkoly nelze provést, dokud nebudou hotovy úkoly jiné, třeba před celkovou opravou bude určitě nutné pořídit náhradní díly a zakoupit správné nářadí. Zároveň některé úkoly nemusí záviset na ničem, například nákup občerstvení na kolaudační večírek či objednání nového nábytku.
Na úkoly lze nahlížet jako na vrcholy orientovaného grafu, kde z vrcholu u do vrcholu v vede hrana právě tehdy, když úkol u závisí na úkolu v. Vrcholy klidně mohou mít víc vstupních a výstupních hran, nicméně se nemůže stát, že by byl v grafu nějaký cyklus.
Můžete předpokládat, že má Kevin vždy k dispozici dostatek pomocné pracovní síly, takže je schopen provádět libovolné množství úkolů najednou.
Při takto rozsáhlém projektu se může snadno stát, že u nějakého úkolu dojde ke zpoždění a veškerá práce bude v důsledku toho dokončena později. Kevin by rád takové situaci předešel a zajímalo by ho, jakých úkolů se to týká.
Vaším úkolem bude pro Kevina vytvořit algoritmus, který obdrží na vstupu doby provedení jednotlivých úkolů, orientovaný acyklický graf jejich závislostí a nalezne všechny úkoly, pro které platí, že jakékoliv malé zpoždění nutně prodlouží nejkratší čas, za který je možné veškerou práci dokončit.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-4-2 Megasněhulák (12 bodů)
36-4-2 Megasněhulák (12 bodů)
Kevin se vracel s kamarády ze školy. Právě přecházeli další z mnoha lyžařských sjezdovek v Hroším Týnci, když narazili na haldu sněhových koulí. Už je ale přestaly bavit soutěže ve stavění sněhuláků, takže se rozhodli spojit síly a postavit jednoho obřího sněhuláka – megasněhuláka.

Rozhodli se, že ke stavbě megasněhuláka použijí právě K koulí. Těchto K koulí poskládají nad sebe. Aby se sněhulák nezhroutil, musí být každá koule ostře menší než ta pod ní. Speciálně tedy není možné použít dvě koule stejné velikosti.
Kevinovi kamarádi rychle změřili velikost každé z N koulí. Každá koule vypadá trochu jinak, a vzhled sněhuláka závisí na každé z použitých koulí. Než se Kevinovi kamarádi rozhodnou, jaké koule použijí, rádi by věděli, kolika způsoby mohou megasněhuláka postavit. Pomůžete jim?
Počet možných megasněhuláků může být opravdu velký, takže stačí, když vypočítáte jeho zbytek po dělení číslem 1 000 000 007.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku budou čísla N a K – počet koulí, které mají Kevinovi kamarádi k dispozici, a počet koulí, které chtějí použít. Na dalším řádku bude N čísel představující celočíselné velikosti dostupných koulí.
Formát výstupu: Na výstup vypište jedno číslo, a to zbytek po dělení počtu možných sněhuláků číslem 1 000 000 007.
5 3 1 2 5 3 3
7
Vysvětlení ukázkového vstupu: Označme koule po řadě 1, 2, 5, 3a a 3b. Kevinovi kamarádi celkem mají sedm různých možností, jak z nich megasněhuláka postavit:
- 5, 2, 1
- 3a, 2, 1
- 5, 3a, 1
- 5, 3a, 2
- 3b, 2, 1
- 5, 3b, 1
- 5, 3b, 2
 36-4-3 Sklad s bednami (13 bodů)
36-4-3 Sklad s bednami (13 bodů)
Kevin se nechal zaměstnat ve velkoskladu jisté firmy specializující se na prodej beden jako skladník. Pracuje v obrovském skladu C-21d, který je vyhrazen pro krychlové bedny velké jeden metr (pro jinak velké bedny má přeci firma jiné sklady).
Jednou v pondělí se ocitl ve skladu úplně sám a začal si hrát. Jezdil s vozíkem různě po skladu a občas, když se mu do cesty připletly nějaké bedny, tlačil je před vozíkem. Když se vydováděl, shledal, že způsobil pěkný chaos. Bedny jsou teď rozesety po skladu na obrovské ploše a nikdo neví kde přesně. Naštěstí si vzpomněl, že vozík si ukládá historii pohybů a ve firemní databázi je zapsáno, kde se nacházely bedny na začátku dne. Jistě tedy půjde dopočítat, kde jsou bedny teď. Pomůžete mu?
Sklad si, protože je opravdu obrovský, můžeme představit jako nekonečnou čtvercovou mřížku. Známe pozice beden předtím, než je Kevin začal posouvat. Dále známe počáteční pozici vozíku a posloupnost jeho pohybů (ve směrech nahoru, dolů, doprava, doleva). Když jede vozík nějakým směrem, tlačí před sebou všechny bedny v daném směru až po tu, před kterou je volné políčko. Na konci nás zajímají všechny pozice, na kterých skončí nějaká z beden (je jedno, která kde, bedny jsou vzájemně nerozlišitelné).
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-4-4 Heslo (10 bodů)
36-4-4 Heslo (10 bodů)
Kevin si stáhl novou aplikaci ministerstva pro byrokracii, kam potřebuje nahrát svoje dokumenty.

Bohužel se ale ukázalo, že vytvořit si účet je trošku složitější…
Zadej heslo dle vyhlášky č. 42:
slavahrosimbohum
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Na odevzdávání úlohy doporučujeme použít ksp-klienta nebo naše API.
 36-4-X1 Počet koček (10 bodů)
36-4-X1 Počet koček (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
„Jů, tady jsou kočky!“ zavýskl Pepíček nad knížkou. Maminka žádnou kočku
neviděla, tak jí musel Pepíček jednu předvést. Prvním chapadlem ukázal na K,
druhým na O v následujícím odstavci, třetím na Č o kus dál, čtvrtým
na další K a pátým na A v posledním řádku. Pak zvesela pokračoval:
„Už jsem jich na téhle stránce našel přes 200. Kolik jich asi bude v celé
kapitole? V celé knížce?“

Pepíček o tom sice ještě neví, ale hodila by se mu datová struktura. Vytvořili bychom ji pro nějaký řetězec k délky K (kočku) a řetězec t délky T (text knížky). Datová struktura by pak uměla pro libovolný (souvislý) podřetězec t[i],… ,t[j] říci, kolikrát se v něm vyskytuje kočka – tedy kolika způsoby lze vybrat indexy a1,… ,ak tak, aby platilo i≤ a0 < a1 < … < aK-1 ≤ j a t[a0] = k[0], …, t[aK-1] = k[K-1].
Navrhněte co nejefektivnější takovou strukturu. Předpokládejte, že struktuře chceme položit řádově T dotazů a že K je mnohem menší než T.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-4-S Nechme stromy růst (12 bodů)
36-4-S Nechme stromy růst (12 bodů)
Právě čtete čtvrtý díl seriálu. Tento díl není přímé pokračování předchozích dílů, ale používají se zde definované termíny z předchozích dílů, které je dobré si vyhledat během čtení nasledujícího textu. Navíc je stále možné odevzdávat úlohy z předchozích dílů seriálu za polovinu bodů.
V prvních dvou dílech jsme se zabývali lineární regresí a jak tento model natrénovat. V třetím díle jsme se podívali, jak rozšířit lineární regresi, aby uměl udělat klasifikaci dat. Tyto modely jsou jednoduché a jedním znakem je, že si neumějí vytvořit nové nelineární featury ze vstupních dat. Navíc trpí ještě jedním nedostatkem – nedokáží odpovědět proč je jejich predikce taková, jaká je. Ano můžete říct, že u tak jednoduchého modelu jako lineární regrese se vysvětlení dá po nějaké chvíli pochopit, ale u složitějších modelů jako jsou neuronové sítě je tento reverse engineering mnohem obtížnější.
V tomto dílu seriálu si ukážeme model, který po natrénování nám dokáže i říct, proč danou predikci udělal. Tento model se bude nazývat rozhodovací strom.
Rozhodovací strom
Jak už název napovídá, tento model má podobu stromu. Každý vnitřní vrchol stromu reprezentuje jednu podmínku, která rozhoduje, kam se máme ve stromu vydat. Predikce modelu vypadá tak, že postupně procházíme vrcholy od kořene stromu dokud se nedostaneme do listu, který nám řekne predikci.
Podmínky se vztahují na jednu featuru z dat. Například: Je teplota pacienta vyšší než 37 stupňů? Pokud ano, pak pokračujte do levého syna, jinak do pravého syna. Odpovědi nemusejí být jen binární (ano/ne), ale mohou být i intervalové. Například: Je teplota pacienta: a) pod 36 stupňů, b) mezi 36 a 37 stupni, c) nad 37 stupňů.
Jak budeme dělat predikce, když se dostaneme do listu? V případě klasifikace budeme predikovat třídu, která je v listu nejčetnější. V případě regrese bude predikce průměr hodnot v listu.
Tento model implicitně dokáže vytvořit zdůvodnění pro každou predikci. Stačí se podívat na cestu, kterou jsme prošli stromem od kořene k listu.
Dříve byl nazýván expertní systém a používal se tímto způsobem: Nejdříve nějaký člověk, expert ve svém oboru, vytvořil sérii podmínek pro klasifikaci či regresi dat. Poté se tento model otestoval na velkém množství dat a podle úspěšnosti se dále upravoval. Tento přístup byl populární v 70. a 80. letech minulého století. Navíc to byly první AI programy, které byly v praxi úspěšné.
My samozřejmě nebudeme tvořit rozhodovací strom ručně, ale pomocí algoritmu.
Stavíme strom
Na začátku si určíme kritérium c, které nám bude říkat, jak rozdílné příklady (data) máme v daném vrcholu. (O výběru kritéria později.) Prozatím si představme, že každý vrchol v má číslo cv, udávající jak moc jsou data rozdílná.
Začínáme s jedním vrcholem (kořenem), kde budeme mít všechna data z trénovacího datasetu.
Poté budeme opakovaně hledat list v, ve kterém jsou „smíchaná co nejvíc nesouvisející data“. Poté nahradíme v za podmínkový vrchol s dvěma syny – listy ℓ, r.
Jak najdeme vrchol, co je nejlepší nahradit? Budeme chtít co nejvíce snížit rozdílnost dat v listech ∑cu. Data v našem listu v pomyslně rozdělíme podle vybrané featury do listů ℓ, r, což nám zmenší součet o Δcv = cℓ+ cr - cv. Ze všech listů vybereme vrchol s největším Δcv a ten doopravdy rozřežeme.
Po zkonstruování stromu můžeme strom ještě lehce prořezat. Občas se ukáže, že nějaký podmínkový vrchol není ve výsledku moc užitečný a můžeme dodatečně nějaké vrcholy odstranit. Důležité je, že prořezávání stromu děláme až po jeho konstrukci. Kdybychom zahazovali na první pohled nezajímavé rozdělení již při konstrukci, tak bychom mohli minout dobrá rozdělení, která by mohla následovat po tomto rozdělení. Knihovna scikit-learn implementuje Minimal Cost-Complexity Pruning algoritmus na prořezávání stromu.
A to je vše. Stojí za zmínění, že data v jednotlivých listech se nemůžou měnit. To znamená, že se nemůže měnit i hodnota kritéria cv pro vrchol v, dokud ho nerozřežeme. Tedy stačí jednou nalézt nejlepší podmínku pro rozdělení dat v listu a poté čekat, dokud se nepoužije.
Z algoritmu není úplně jasné, proč vybíráme vrchol, kde klesne nejvíce naše sledované kritérium, protože dřív nebo později rozdělíme všechny listy (máme jen konečný počet dat).
Děláme to z toho důvodu, že na rozhodovací stromy dáváme dodatečná omezení. Nejběžnější omezení jsou tato:
- Maximální hloubka stromu. Strom může mít maximálně hloubku d.
- Minimální počet dat na rozdělení. Pokud je počet dat v listu je menší než n, tak daný list již nedělíme.
- Maximální počet listů. Strom může mít maximálně ℓ listů.
Nyní zbývá poslední otázka, a to, jaké kritérium použijeme? Ukažme si různá rozdělení dat a porovnáme jejich vhodnost. Máme 8 dat a chceme naučit strom pro klasifikaci. 4 data patří do třídy A a 4 data do třídy B. Nechť máme dvě možná rozdělení dat: Jedno rozdělení rozdělí data do dvou listů, kde v každém listu budou 2 data z třídy A a 2 data z třídy B. Druhé rozdělení rozdělí data také dvou listů, kde v jednom listu budou 3 data z třídy A a 1 dato z třídy B a v druhém listu 1 dato z třídy A a 3 data z třídy B. Jaké rozdělení je lepší? Očividně druhé rozdělení je lepší. Představme si, že bychom použili první rozdělení a po tomto rozdělení vrcholu by konstrukce stromu skončila. V tomto případě bychom si vůbec nepomohli, protože místo jednoho vrcholu, kde poměr tříd byl 1:1, máme dva vrcholy se stejným poměrem.
Náš cíl je najít metriku, která bude zachycovat nějakou vlastnost rozdělení. Nejdříve se podíváme na klasifikaci, ale poté uvedeme kritérium i pro regresi.
Míra informace (self-information)
Míra informace (self-information) je množství „překvapení“, že nastane daný jev. Toto může znít trochu zvláštně, ale zkusme si to vysvětlit na příkladu. Když vám řekneme, že zítra vyjde slunce, tak vás to moc nepřekvapí, protože pravděpodobnost je velmi vysoká (pomineme-li případ, že bude zataženo). Naopak pokud vám řekneme, že v červenci bude sněžit, tak to bude velice překvapivé, protože pravděpodobnost je velmi malá.
V kontextu rozhodovacího stromu máme v každém listu určitý počet příkladů, které patří do nějaké třídy (jeden jev odpovídá jedné třídě). Z těchto dat můžeme vytvořit empirickou distribuci (viz. třetí díl seriálu).
Formálně je míra informace definována pomocí sady podmínek a z těchto podmínek i vyjde, jak vypadá předpis míry informace.
- míra informace má být rovna nule, pokud je daný jev jistý (pravděpodobnost je 1)
- méně pravděpodobné jevy mají větší hodnotu (jsou více překvapivé)
- pro nezávislé jevy musí být hodnoty míry informace sčitatelné
Díky třetí podmínce přesně dostaneme předpis pro míru informace. Pro nezávislé jevy se pravděpodobnosti násobí, definice však požaduje sčítání. Operaci násobení převést sčítání dokážeme provést pomocí logaritmu.
Míra informace (I) je definována jako:
| 1 |
| p |
kde p je pravděpodobnost daného jevu.
Entropie
S mírou informace souvisí pojem entropie. Entropie je střední hodnota míry informace pro celou distribuci. Střední hodnota se počítá jako vážený průměr. V našem případě se střední hodnota počítá tak, že vynásobíme pravděpodobnost daného jevu s hodnotou daného jevu – hodnotou míry informace jevu a tyto součiny sečteme.
Jinými slovy, entropie udává průměrné množství překvapení v celé pravděpodobnostní distribuci.
Kritérium dělení pro klasifikaci
Z teorie výše můžeme vytvořit kritérium na bázi entropie:
| K |
| i=1 |
kde v odpovídá vrcholu ve stromě, |v| je počet příkladů v daném vrcholu, K je počet klasifikovaných tříd a pi je pravděpodobnost, že náhodně vybraný příklad patří do třídy i. H(v) je entropie daného vrcholu.
Další možné kritérium se kterým se můžete setkat je Gini index či Gini impurity. Toto kritérium měří, jak často je náhodně vybraný příklad z daného vrcholu v špatně klasifikován, když danému datu přiřadíme náhodnou třídu z distribuce tříd daného vrcholu v.
| K |
| i=1 |
kde pi je pravděpodobnost, že vybereme náhodně danou třídu a 1 - pi je pravděpodobnost, že této třídě přiřadíme špatnou třídu. Toto provedeme |v| krát, protože máme |v| příkladů v daném vrcholu v.
Kritérium entropie se dá odvodit z NLL chybové funkce, tedy není to náhodná věc, kde si jen lidé řekli, že je to dobrý nápad na kritérium. Gini index pro dvě třídy se dá odvodit z MSE (tedy jen SE) chybové funkce.
Obě kritéria jsou si dost podobná. Jedna z výhod Gini indexu je, že je rychlejší na výpočet, protože nepočítá logaritmus. Na druhou stranu kritérium entropie je více preferováno, když jsou data nevyvážená, tj. když mezi jednotlivými třídami je velký rozdíl v počtu dat v datasetu. V praxi ale stejně chcete vyzkoušet obě kritéria a vybrat to, které dává lepší výsledky.
Kritérium dělení pro regresi
Pro regresní kritérium se inspirujeme prvním dílem seriálu a použijeme MSE chybovou funkce, tedy spíše jen SE chybovou funkci (nebudeme počítat odmocninu).
| |v| |
| i=1 |
kde v odpovídá vrcholu ve stromě, |v| je počet příkladů ve vrcholu v, yi je target (hodnota, kterou chceme predikovat) pro dané dato i a yˆ je predikce, která se vytvoří ve vrcholu v.
Úkol 1 – Rozhodovací stromy [8b]
Naprogramujte rozhodovací stromy. Pro lehčí implementaci jsme připravili šablonu, která načítá různé parametry jako je použitý dataset a omezení pro konstrukce stromů. Budeme používat dva datasety, jeden pro klasifikaci a druhý pro regresi. Pro regresi použijte kritérium cSE a pro klasifikaci kritérium centropie.
Můžete odevzdávat i částečná řešení a dostat za ně částečné body. Minimálně ale musíte implementovat jedno kritérium a jedno omezení pro konstrukci stromu.
Ukázky použití (výstupy byste měli mít stejné). K příkladům připojujeme i ilustrace stromů. První řádek vrcholů říká podmínku pro rozdělení (pokud vrchol není list). Další řádek říká počet dat ve vrcholu a poslední řádek je predikce pro daný vrchol. U klasifikace jednotlivé hodnoty v poli znamenají, kolik dat patří do dané třídy.
python decision_tree.py --dataset diabetes --min_to_split=60
Train RMSE: 54.13917
Test RMSE: 58.95506
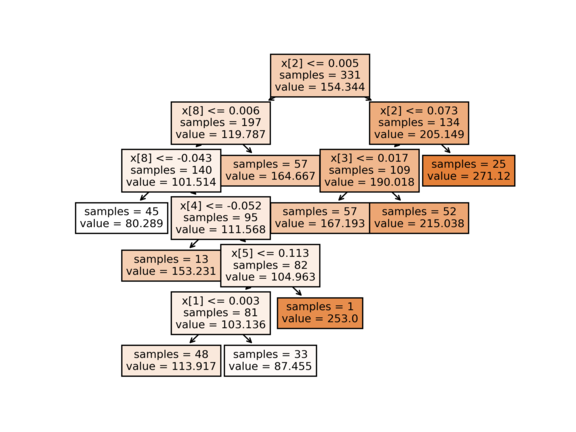
python decision_tree.py --dataset diabetes --max_depth=2
Train RMSE: 58.28164
Test RMSE: 60.41034
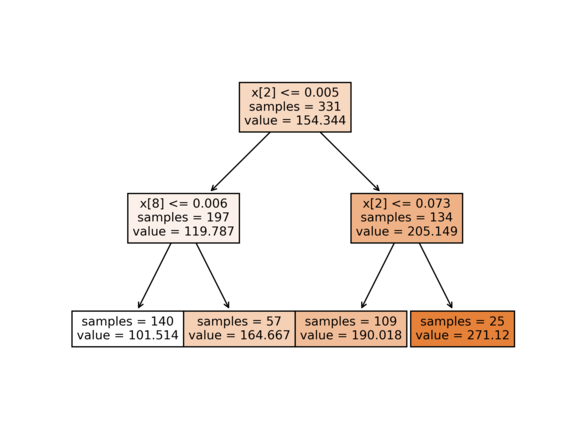
python decision_tree.py --dataset diabetes --max_leaves=6
Train RMSE: 55.47440
Test RMSE: 58.58354
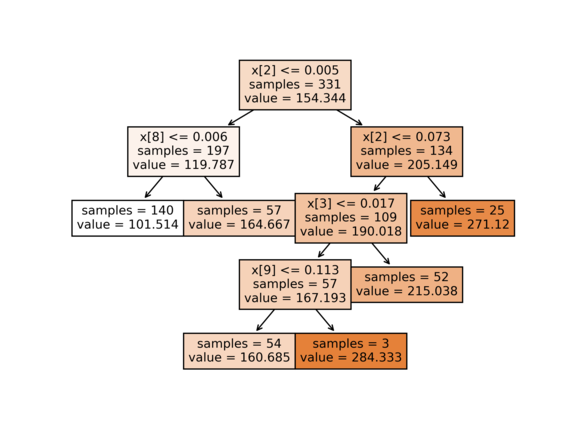
python decision_tree.py --dataset diabetes --max_depth 3 --max_leaves=6
Train RMSE: 55.84286
Test RMSE: 58.72956
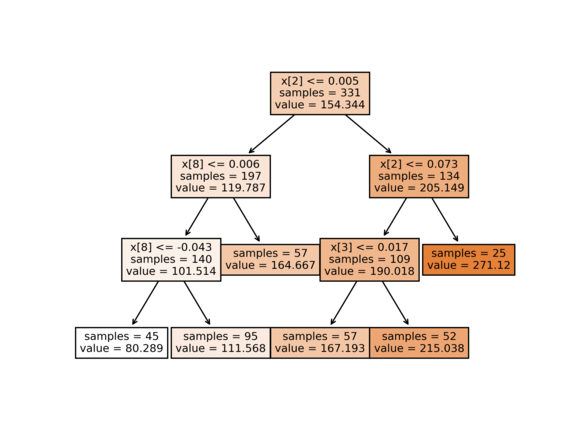
python decision_tree.py --dataset wine --min_to_split=60
Train accuracy: 91.0%
Test accuracy: 86.7%
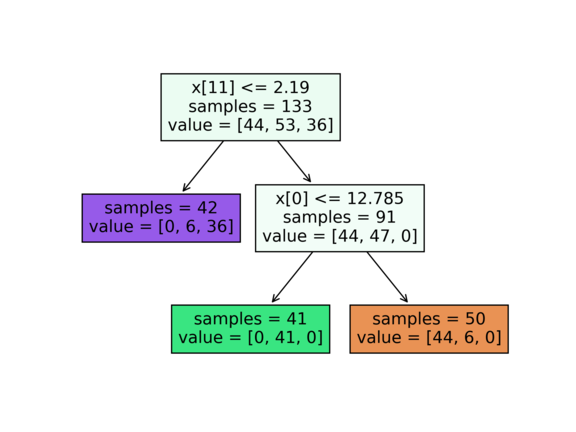
python decision_tree.py --dataset wine --max_depth=2
Train accuracy: 94.0%
Test accuracy: 88.9%
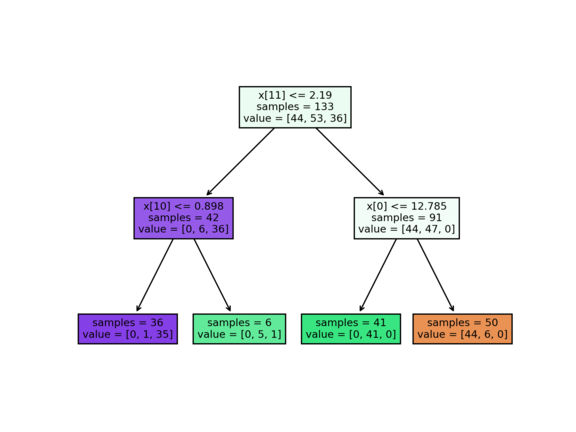
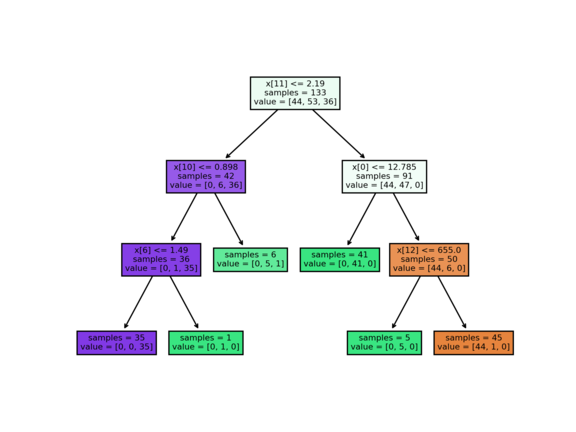
python decision_tree.py --dataset wine --max_leaves=6
Train accuracy: 98.5%
Test accuracy: 91.1%
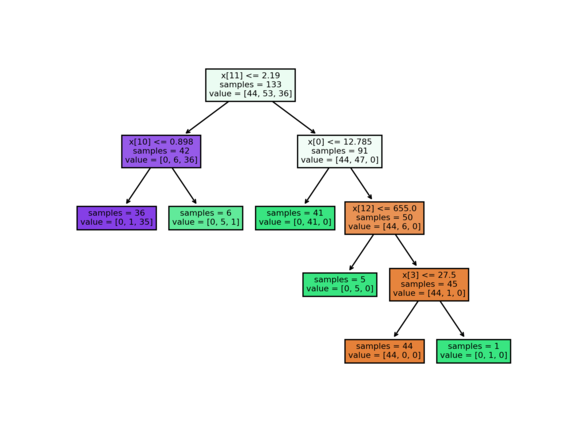
python decision_tree.py --dataset wine --max_depth 3 --max_leaves=6
Train accuracy: 98.5%
Test accuracy: 88.9%
Random Forest
Když se podíváme na rozhodovací stromy, tak tyto modely jsme docela dost omezovali, abychom předešli overfittingu. Co když omezíme stromy ještě více a místo jednoho modelu, který bude predikovat, použijeme více modelů a výsledek spočítáme průměrem (pro regresi), nebo hlasováním (pro klasifikaci)? Tento model se nazývá Random Forest.
V této myšlence je menší problém, že při stejných parametrech a datech budou jednotlivé stromy stejné. Proto využijeme dvě techniky:
- Bagging neboli (bootstrap aggregation) je technika, kde pro každý model vytvoříme jiný dataset. Tento dataset vytvoříme tak, že z původního datasetu o velikosti n dat náhodně vybereme n dat s opakováním. Tímto způsobem dostaneme nový dataset, který bude mít podobnou distribuci jako původní dataset, ale bude se lišit v konkrétních datech. Například jeden model uvidí jeden příklad třikrát a jiný příklad vůbec. Tím docílíme toho, že jednotlivé modely se naučí jiné vlastnosti dat.
- Feature subsampling – při každém dělení vrcholu vybereme jen část feature z dat, které budeme brát v potaz, když budeme dělit vrchol (ostatní featury pro dané dělení nebudou použity). Tato technika přispívá k tomu, aby jednotlivé stromy byly různé i když použijeme stejný dataset.
Existují i další techniky, které se používají, ale tyto dvě jsou nejběžnější.
Úkol 2 – Random Forest [4b]
Naprogramujte Random Forest. Pro lehčí implementaci jsme připravili šablonu, která načítá různé parametry jako počet konstruovaných stromů a omezení pro konstrukce stromů. Tuto úlohu je dobré řešit až po první úloze, protože se očekává, že použijete naimplementované řešení z první úlohy. Na rozdíl od první úlohy, ale budeme dělat jen klasifikaci a jediné omezení pro konstrukci stromů bude maximální hloubka stromu.
Ukázky použití (výstupy byste měli mít stejné)
python random_forest_solve.py --trees 10 --max_depth=3
Train accuracy: 54.4%
Test accuracy: 50.4%
python3 random_forest.py --trees=10 --bagging --max_depth=3
Train accuracy: 72.8%
Test accuracy: 72.2%
python3 random_forest.py --trees=10 --feature_subsampling=0.5 --max_depth=3
Train accuracy: 64.3%
Test accuracy: 62.7%
python3 random_forest.py --trees=10 --bagging --feature_subsampling=0.5 --max_depth=3
Train accuracy: 73.5%
Test accuracy: 75.6%
Ensembling
Ensembling neboli kombinace modelů je technika, kde pro predikci použijeme více modelů a výsledek spočítáme průměrem (pro regresi) nebo hlasováním (pro klasifikaci). Random Forest je jeden z příkladů kombinace modelů. Tuto techniku stejně jako např. bagging, můžeme použít i u jiných modelů. Ensembling se velice hodí, pokud máte více modelů, které můžou dělat různé systematické chyby na nějakých příkladech. Kombinací těchto modelů můžeme dosáhnout lepších výsledků, ale v praxi spíš dojde k průměru výsledku na dané metrice. To se nemusí zdát jako nejlepší věc, co udělat, ale někdy se třeba nemůžeme rozhodnout jaký model použít, tak použijeme všechny. Ensembling je dobré většinou dělat na třech až pěti modelech (toto neplatí pro stromy, kde se ensembling dělá z mnoha malých modelů). Více modelů se spíše nepoužívá, protože samotná predikce na jednom modelu trvá nějaký čas a více neznamená vždy lépe. Ensembling můžeme použít i na různé modely, což máme ukázáno v následujícím příkladu.
from sklearn.datasets import load_iris
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
lr = LogisticRegression()
dt = DecisionTreeClassifier()
data, target = load_iris(return_X_y=True)
model = VotingClassifier([
('lr', lr), ('dt', dt)
])
model.fit(data[:-1], target[:-1])
model.predict(data[-1:])
Bohužel VotingClassifier nefunguje způsobem, že byste dali již
natrénované modely a na nich provedli hlasování. Což je trochu škoda,
protože většinou natrénujeme více modelů a poté je chceme spojit.
Naštěstí napsat si tuto funkcionalitu není složité, stačí k tomu obyčejné
pole.
Úkol 3 – Soutěžní úloha [3b]
Jako poslední úkol bude soutěžní úloha. Z technických důvodů je soutěž zadaná jako samostatná open-datová úloha 36-4-S2, kterou najdete níže. Zdrojový kód soutěžního programu ale přidejte do ZIPu s řešením seriálu.
Všechny úlohy z tohoto seriálu odevzdávejte dohromady v jednom zazipovaném archivu. Termín odevzdání je 19. května ve 32:00 (tedy další ráno v 8:00). Poté lze odevzdávat za snížený počet bodů až do konce ročníku.
Mějte se fanfárově a posledním díle se podíváme na učení bez učitele (unsupervised learning)!
 36-4-S2 Soutěžní úloha seriálu (3 body)
36-4-S2 Soutěžní úloha seriálu (3 body)
Z technických důvodů je 3. úkol seriálu oddělenou úlohou. Odevzdává se jako open-datová úloha 36-4-S2, ale prosíme přiložte do zazipovaného archivu k seriálu i svá řešení tohoto úkolu. Pokud to neuděláte, můžeme vám dodatečně body odebrat.
V této soutěži je povolené používat libovolné modely
ze scikit-learn modulů sklearn.tree,
sklearn.ensemble a sklearn.linear_model.
Je zakázáno používat jiné modely implementované
v knihovně scikit-learn jako MLP, …
Jak soutěž bude probíhat? Od nás dostanete trénovací a testovací data. Dále od nás dostanete šablonu, která si v případě potřeby data stáhne a načte vám data. U trénovacích dat budete mít k dispozici vstupní featury a výstupní hodnoty, ale u testovacích dat budete mít k dispozici jen vstupní featury. Vaším úkolem je natrénovat model na trénovacích datech a predikovat výstupní hodnoty pro testovací data. Dataset můžete různě transformovat (augmentovat), ale nesmíte si přidávat další externí data do trénovacího datasetu. Všechny výstupy musí být generované vaším programem. Toto pravidlo nezakazuje mít v programu pravidla, která výstupy upravují. Tyto predikce poté odevzdáte do odevzdávátka.
Vaším úkolem je vypredikovat, jaká číslice se nachází na obrázku.
Pokud vaše řešení bude splňovat, že na testovacích datech budete mít přesnost (accuracy) minimálně 94,% (této hodnotě budeme říkat práh), tak dostanete 3 body. Tím ale zábava teprve začíná, protože tímto krokem jste se kvalifikovali do soutěže.
V soutěži budete soutěžit s ostatními řešiteli až o další 3 bonusové body. Abyste věděli, jak si stojíte, tak k této úloze je i dynamická výsledkovka. Na této výsledkovce uvidíte svou accuracy metriku na testovacích datech nebo hodnotu prahu, podle toho, jaká hodnota je horší. Dále na této výsledkovce budete řazeni podle accuracy metriky na testovacích datech. Pokud jste v soutěži, tak sice neuvidíte accuracy metriku, ale pořád budete vědět, kolik lidí je lepší než vy.
Bonusové body se budou udělovat podle následujícího kritéria: Nejlepší první čtvrtina řešitelů řazená podle accuracy metriky, která se kvalifikovala do soutěže, dostane 3 body, druhá čtvrtina dostane 2 body a třetí čtvrtina dostane 1 bod. Bonusové body budou přiděleny po prvním deadlinu pro tento díl seriálu.
Hodně štěstí!