Pátá série třicátého šestého ročníku KSP
Celý leták v PDF.
Dostává se k vám páté číslo hlavní kategorie 36. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: neděle 23. června 2024 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo získá alespoň 2 body z každého dílu seriálu.
Zadání úloh
- 36-5-1: Opravování opravy vzducholodi
- 36-5-2: Polygloti
- 36-5-3: Všechny cesty vedou do Říma
- 36-5-4: Hackovaci soutez
- 36-5-S: Učení bez učitele
- 36-5-S2: Soutěžní úloha seriálu
- 36-5-X1: Superstring
 36-5-1 Opravování opravy vzducholodi (10 bodů)
36-5-1 Opravování opravy vzducholodi (10 bodů)
Organizátoři KSP se radují. Aby ne, když jim přišlo celkem N řešení úlohy 36-4-1! Bojí se jen, že jim bude trvat dlouho všechna řešení opravit.
Organizátoři se proto pokusili vytrénovat jazykový model, který by řešení opravil za ně. Moc úspěchu ale neměli: nejen že se jim nepodařilo modelu vysvětlit vzorové řešení, ale navíc se bojí, že když některý z účastníků nevyhnutelně vymyslí nějaké originální, netradiční řešení, tak ho jazykový model nepozná a zamítne. Podařila se jim však jedna věc: model naučili zhodnotit složitost a čitelnost daného řešení a na základě toho přesně spočítat, jak dlouho bude organizátorovi trvat ho opravit ručně.
Existuje K organizátorů, kteří mají čas řešení opravovat. Plánují se sejít a řešení si mezi sebou rozdělit. Každý organizátor postupně opraví všechna svá řešení, každé přesně za dobu předpovězenou jazykovým modelem. Opravování bude hotovo, jakmile svá řešení doopraví poslední z organizátorů.
Bohužel došel inkoust ve stroji, který řešení orazítkovává čárovými kódy, takže se organizátoři bojí, že se jim řešení pomíchají. Řešení si proto seřadili abecedně podle jména autora a každému organizátorovi plánují přidělit nějaký souvislý úsek.
Organizátoři by rádi řešení opravili co nejrychleji, aby mohli spolu jít na zmrzlinu. Poradíte jim, jak si mají řešení rozdělit?
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku budou dvě přirozená čísla: počet řešení N a počet organizátorů K. Na druhém řádku bude N přirozených čísel T1 až TN, časy potřebné k opravení jednotlivých řešení v mikrosekundách. Řešení jsou uvedena v tom pořadí, jak si je organizátoři abecedně seřadili.
Formát výstupu: Za každého opravujícího organizátora vypište jeden řádek s dvěma čísly a a b, číslo prvního a posledního řešení (včetně), které má daný organizátor opravit. Těchto řádků můžete vypsat nejvýše K.
6 3 4 1 6 10 1 2
1 3 4 4 5 6
Vysvětlení ukázkového vstupu: Prvnímu organizátorovi bude opravování trvat 11 mikrosekund, druhému 10 mikrosekund a třetímu 3 mikrosekundy. Opravování tedy bude hotovo za 11 mikrosekund, což je tak rychle, jak to jen jde.
 36-5-2 Polygloti (12 bodů)
36-5-2 Polygloti (12 bodů)
Honza se Šimonem byli ze školy vysláni na Konferenci sudokopytných polyglotů v Hrochschwabu, aby tam předali své znalosti hřečtiny. Nejprve ale potřebují vymyslet nějakou rozumnou trasu, kterou se dostat do tak daleké krajiny. Zároveň by si po cestě rádi zopakovali jazyky ostatních zemí. Pokud se totiž účastník konference zvládne domluvit s jakýmkoliv jiným účastníkem v jeho rodné řeči, vyhraje zlaté parohy.

Aby se navzájem motivovali ve cvičení jazyků, domluvili se Honza a Šimon na následujícím postupu: oba nejprve začnou putování v jejich domovském městě Hroška. Jakmile se jejich cesty rozdělí, začnou se oba samostatně učit nějaký nový jazyk. Až se jejich cesty zkříží, promluví si spolu tímto jazykem, obohativše se navzájem díky různým přístupům k učení. Jakmile se po nějaké chvíli zase rozejdou, celý proces se zopakuje s dalšími novými jazyky, a tak dále, dokud se jim nepodaří setkat se v Hrochschwabu.
Oba kamarádi by rádi své cesty naplánovali tak, aby se během nich naučili co nejvíce jazyků. Jinými slovy, chtějí se na cestách co nejvíckrát rozejít a zase sejít. Pomůžete jim?
V našem světě existuje celkem N měst očíslovaných 1 až N podle toho, jak vysoko se nachází – nejníže položené město má tedy číslo 1. Jelikož chodit z kopce je nuda, cesty mohou vést pouze z níže položených měst do vyšších. Z i-tého města potom vedou jednosměrky do ni dalších měst, a to pouze těch, které mají číslo větší než i. Hroška má číslo vs a Hrochschwab má číslo vc, přičemž vs ≠ vc.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku vstupu dostanete zadané hodnoty N,vs,vc. Na dalších N řádcích obdržíte postupně popisy jednotlivých měst: i-tý řádek začíná číslem ni. Za ním následuje ni vzestupně řazených čísel měst, do kterých vede z i-tého města jednosměrka.
Formát výstupu: Nechť vámi nalezená Honzova a Šimonova cesta navštěvuje H, respektive S měst. Na prvním řádku vypište H mezerami oddělených čísel měst popisujících postupně Honzovu cestu, tedy prvním číslem musí být vs a posledním vc. Na druhém řádku vypište ve stejném formátu Šimonovu cestu. Pro tyto dvě cesty musí platit, že se na nich oba kamarádi co nejvíckrát rozejdou a zase potkají. Cesty nemusí být hranově disjunktní, je tedy povoleno, aby občas mezi dvěma městy cestovali Honza a Šimon spolu. Pokud existuje více stejně dobrých cest, vypište libovolnou z nich. Máte zaručeno, že mezi Hroškou a Hrochschwabem existuje aspoň jedna cesta.
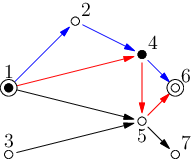
7 1 6 3 2 4 5 1 4 1 5 2 5 6 2 6 7 0 0
1 2 4 6 1 4 5 6
 36-5-3 Všechny cesty vedou do Říma (12 bodů)
36-5-3 Všechny cesty vedou do Říma (12 bodů)
Adam a Kačka se rozhodli udělat si pochod z Benátek do Říma. Sbalili si, nasedli na vlak a vyjeli do Benátek. Když jeli kolem hranic, tak se Adam rozhodl si protáhnout nohy a projít se po vlaku. Nicméně chvíli potom rozpojili vlak, a když se Adam snažil domluvit s průvodčím, dostalo se mu pouze odpovědi: „Non riesco a capirti.“
Nyní je Kačka v Benátkách a Adam je v Miláně. Nicméně i přesto se rozhodli udělat pochod do Říma. To udělají tak, že v současném městě zkusí se svou omezenou schopností italštiny zjistit, kterým směrem je Řím. Poté tímto směrem půjdou, dokud nedojdou do dalšího města, kde proces zopakují. Kačku a Adama nyní zajímá, kde se poprvé potkají.
Trochu formálněji: Vrcholy grafu Itálie tvoří města, kde každý vrchol má právě jednu výstupní hranu. Pokud začneme v libovolném vrcholu, a budeme z něj následovat hrany, časem dojdeme do Říma. Kačka stojí ve vrcholu b a Adam ve vrcholu m. Chtěli bychom najít první vrchol, kterým projdou oba.
Nicméně graf Itálie není malý, proto požadujeme, aby algoritmus kromě uložení grafu samotného používal jen konstantně mnoho paměti. Navíc pokud se Adam a Kačka budou se svou omezenou schopností italštiny ptát místních na směr do Říma a vždy se tímto směrem vydají, nejspíš nepůjdou úplně přímou cestou.
Proto určujte složitost algoritmu vzhledem k těmto parametrům:
- Sb – Vzdálenost Benátek a prvního společného města
- Sm – Vzdálenost Milána a prvního společného města
- Rb – Vzdálenost Benátek a Říma
- Rm – Vzdálenost Milána a Říma
- N – Počet vrcholů
- M – Počet hran
Například, kdybychom měli následující algoritmus, který je sice funkční, ale nepoužívá konstantní množství paměti:
- Najdeme všechny vrcholy na cestě B z Benátek do Říma O(Rb)
- Najdeme všechny vrcholy na cestě M z Milána do Říma O(Rm)
- Pro každý vrchol z B se podíváme, jestli se vyskytuje na cestě M. První, který se vyskytuje je náš hledaný. Protože takto budeme zkoušet vrcholy z B od začátku do prvního společného města, složitost bude O(Sb Rm)
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-5-4 Hackovaci soutez (11 bodů)
36-5-4 Hackovaci soutez (11 bodů)

Kačka na poslední Smršti navštívila přednášku o háčkování. To ji velmi nadchlo, koupila si háčky všech možných velikostí a příze všech možných barev a začala každou chvíli svého volného času vyplňovat háčkováním. Kromě řetízkového stehu se naučila háčkovat různě dlouhé sloupky, ubírat a přidávat oka a vyzkoušela si i některé složitější vzory. O pár dní později už byl její pokoj plný malých háčkovaných chobotniček.
Dokážete si představit Kaččino nadšení, když na chodbě ve škole zahlédla plakát s velkým nápisem „Hackovaci soutez“. Samozřejmě dlouho nemeškala, na uvedené adrese se přihlásila a začala ještě více trénovat, aby ji na soutěži nic nepřekvapilo.
První podezření, že se někde stala chyba, pojala Kačka, když přicházela na místo soutěže. Místo lidí s košíky barevné příze, háčky a různobarevnými kusy oblečení všude okolo sebe viděla ostré hochy, ostrá děvčata a další ostré bytosti v černých mikinách, kteří u sebe neměli ani háčky, ani přízi, ale velké těžké staré notebooky. Další dávku podezření pojala na recepci, kde, když řekla, že přišla na „Háčkovací soutěž“, se na ní dívali poněkud zvláštně, než ji navedli správným směrem.
Všechno se vyjasnilo, až když soutěž začala a Kačka si přečetla zadání první úlohy. Vůbec totiž nebyla na Háčkovací, ale na Hackovací soutěži! Rozhodla se ale, že se jen tak jednoduše nevzdá a vyřeší alespoň jednu úložku. Pomůžete jí?
Na serveru běží následující program:
void print_flag1() { /* ... */ }
void print_flag2() { /* ... */ }
char skutecneheslo[40];
int main() {
// ...
bool ok = false;
char heslo[40];
printf("Zadejte heslo: ");
gets(heslo);
if (strcmp(heslo, skutecne_heslo) == 0)
ok = true;
if (ok)
print_flag1();
else
printf("\nŠpatné heslo.\n");
}
Některé části kódu jsou úmyslně vynechané, celý zdrojový kód najdete zde.
K řešení máte k dispozici přímo zkompilovaný program, takový, jaký běží na serveru.
Vaším úkolem je zařídit, aby se spustily print_flag1() a
print_flag2(), přičemž máte přístup pouze k standardnímu vstupu a
výstupu programu, které jsou připojené přímo na TCP socket na adrese vm.kam.mff.cuni.cz a portu 13337. Na ten se můžete připojit například
pomocí příkazu nc vm.kam.mff.cuni.cz 13337, na Windows pomocí PuTTY v
režimu Raw nebo pomocí knihovny socket v Pythonu.
K řešení se vám bude hodit mít k dispozici nějaké Linuxové prostředí, nějaký
disassembler (není potřeba nic složitého jako IDA nebo Ghidra, bohatě vám
postačí objdump -S), abyste se mohli podívat, na jakých adresách jsou
části programu uložené a debugger, například gdb, abyste se mohli podívat,
co program dělá, když mu dáte různé vstupy. Zajímavé také může být prozkoumat
knihovnu pwntools, ale tuhle úlohu zvládnete vyřešit i bez ní. Nakonec,
nezapomeňte si přečíst naši novou kuchařku o práci s pamětí, která vychází součástí této série. Kdybyste narazili během
řešení na nějaký problém, nebojte se zeptat
na Discordu nebo emailem. Na
Discordu ale dávejte pozor, abyste neodhalili část postupu řešení.
Tohle je experimentální open-data úloha. Když úlohu vyřešíte, vypadnou na vás
dvě různé vlajky ve formátu ksp{.*}. Každá je správnou odpovědí na
jeden ze vstupů v odevzdávacím systému. Odpověď na první vstup vypisuje funkce
print_flag1() a na druhý vstup funkce print_flag2(). Když se vám
podaří získat jenom jednu z nich, dostanete jen část bodů.
 36-5-X1 Superstring (10 bodů)
36-5-X1 Superstring (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
Byl jednou jeden Medvěd a ten měl šuplík, kde schraňoval svou sbírku zajímavých řetězců. Teď zatřídil pár nových úlovků, ale co to? Šuplík už nejde zavřít. Napadlo ho, že když mají řetězce spoustu společných částí, mohl by je rozebrat na kousíčky a složit z nich jediný řetězec, v němž se budou nacházet všechny původní podřetězce. Jak ale takový řetězec najít?
Navrhněte algoritmus, který dostane n řetězců o celkové délce m znaků z nějaké malé konečné abecedy Σ. Na výstupu pak vypíše nejkratší možný řetězec, jehož (souvislým) podřetězcem bude každý ze zadaných řetězců.
Jelikož to v polynomiálním čase nikdo neumí (třeba budete první), spokojíme se s časovou složitostí O(2n·poly(m, |Σ|)).
 36-5-S Učení bez učitele (12 bodů)
36-5-S Učení bez učitele (12 bodů)
Právě čtete poslední díl seriálu. Stejně jako minulý díl i tento díl seriálu není přímé pokračování předchozích dílů, ale používají se zde definované termíny z předchozích dílů, které je dobré si vyhledat během čtení následujícího textu. Navíc je stále možné odevzdávat úlohy z předchozích dílů seriálu za polovinu bodů.
V tomto díle se podíváme na strojové učení bez učitele. Poté se podíváme ještě na pár nesourodých algoritmů, které budeme trénovat klasicky – učením s učitelem. Podíváme se na nejjednodušší neuronové sítě a na algoritmus KNN.
Učení bez učitele je velmi zvláštní úloha. Co by název mohl napovídat je, že řekneme počítači (modelu): „Tady máš data a snaž se,“ ale takto modely nefungují. Modely se nesnaží číst myšlenky uživatele a nesnaží se podle daného datasetu uhodnout úlohu a poté vygenerovat odpověď na základě dodaných dat. Typicky máme data a nějaký cíl, i když přesně nevíme, jak vypadá. Například máme síťovou komunikaci a chceme detekovat anomálie (např. síťové útoky). Dopředu se nedá říct, jak vypadají anomálie, protože v každé síti je jiná běžná komunikace a něco, co by v jedné síti bylo anomálií, v jiné může být zcela normální.
Jiným příkladem učení bez učitele je například generování obrázků způsobem, že dáme modelu pár obrázků a má vygenerovat další podobné obrázky. Nebo dáme modelu dataset obrázků od jednoho malíře a poté chceme na náš obrázek aplikovat styl tohoto malíře.
Tyto aplikace jsou už celkem komplikované a byly by na delší povídání, tak si ukážeme jednodušší model. Představme si, že máme spoustu fotek a chceme je rozdělit podle podobností. Například máme kolekci fotek UwU kočiček, hrozivých pejsků a růžových pandiček. Řekněme, že jste vášnivý fotograf a máte tisíce těchto fotek a nechce se vám je ručně třídit. Naším cílem je vytvořit model, který rozdělí obrázky do skupin (clusterů) podle podobnosti. Samozřejmě toto rozdělení nebude dokonalé a může obrázky rozdělit do jiných skupin než očekáváme (dost záleží na funkci, která porovnává podobnosti obrázků), ale také nám může ušetřit dost času s úvodním rozdělením obrázků a můžeme opravit případné chyby ručně.
K-means
Popíšeme si jednoduchý algoritmus, který na vstupu dostane dataset a počet skupin (clusterů), do kterých má data rozdělit. Model poté vrátí rozdělení dat do skupin. Tento algoritmus se nazývá K-means.
Na vstupu dostaneme počet skupin K. Náhodně vybereme K dat ze vstupního datasetu a označíme je jako středové body. Každé dato patří do právě jedné skupiny a skupina se určí podle toho, ke kterému středu je dato nejblíže.
Např. mějme dataset o 12 příkladech a K=3. Každý příklad má dvě featury – x-ovou a y-ovou souřadnici bodu. Náhodně vybereme tři příklady z dat a všechny data rozdělíme podle nejbližšího středu. Středy jsou označeny červeným symbolem X a jsou vyplněny barvou pro danou skupinu. Data odpovídající dané skupině jsou označena odpovídající výplňovou barvou středu.
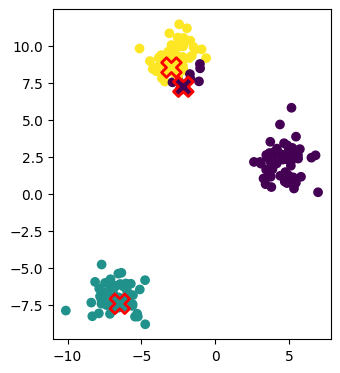
V příkladu pro určení vzdálenosti mezi daty a středy jsme použili euklidovskou vzdálenost, ale v obecnosti můžeme použít libovolnou metriku (funkci, která určuje vzdálenost mezi dvěma daty).
Poté pro každou skupinu vypočítáme nový střed. Nový střed je průměr všech dat, které do skupiny patří. Určíme nové rozdělení dat podle nových středů. Znovu spočítáme středy a takto pokračujeme, dokud se středy mění.
Když vypočítáme nové středy z příkladu výše a zobrazíme si rozdělení dat podle těchto středů, tak obrázek bude vypadat následovně.

Po skončení algoritmu známe finální středy skupin, tedy známe i rozdělení dat do skupin. Když se podíváme na algoritmus, tak jeho cíl je minimalizovat součet vzdáleností dat od středů. Najít skutečné minimum je NP-těžký problém, ale algoritmus najde nějaké lokální minimum.
S tím souvisí několik poznámek.
- Výsledek algoritmu závisí na počátečních středech. Pokud zvolíme špatné středy, můžeme se dostat do lokálního minima, které nemusí být pro nás dobré.
- U euklidovské vzdálenosti máme zaručeno, že algoritmus skončí, ale u jiných metrik tato vlastnost už nemusí platit.
- U euklidovské vzdálenosti je sice zaručeno, že algoritmus skončí, ale není zaručeno, jak rychle skončí. Pro různé počáteční středy algoritmus bude pracovat různě dlouho. Dokonce i ve dvou dimenzích může algoritmus zkonvergovat až po exponenciálním počtu kroků. Proto se omezuje i maximální počet iterací algoritmu.
Většinou se tento algoritmus spouští několikrát a z výsledků se vybere ten, který má nejmenší součet vzdáleností dat od středů.
Úkol 1 – K-means [4b]
Naprogramujte algoritmus K-means. Pro lehčí implementaci jsme připravili šablonu, která načítá různé parametry jako je počet hledaných skupin a počet iterací. Dále šablona vygeneruje náhodná data a vybere počáteční středy. Dále si můžete po každém kroku algoritmu vykreslit aktuální rozdělení dat do skupin a jejich středy.
Ukázky použití (výstupy byste měli mít stejné). Pro každý příklad připojujeme obrázek, který ilustruje průběh algoritmu.
python kmeans.py --iterations 2
Přiřazené skupiny:
[1 0 1 1 1 0 2 1 1 2 0 2 2 0 2 1 2 0 2 2 1 0 0 1 2 2 0 2 1 0 2 1 1 2 1 2 0
0 0 1 0 1 1 1 1 0 2 0 1 2 1 0 0 2 0 1 2 0 2 0 0 1 1 1 0 1 1 2 0 1 0 0 2 0
2 2 1 0 2 1 2 2 0 0 0 1 2 0 1 1 2 0 2 2 1 1 0 0 0 1 2 2 2 1 0 0 0 1 0 1 2
2 0 0 0 2 0 2 1 0 0 2 0 1 2 0 0 2 0 2 2 2 1 0 0 1 2 2 2 0 2 2 1 0 0 1 2 1
0 2 0 2 1 2 1 2 1 2 1 1 2 2 1 1 2 1 1 0 0 1 2 0 1 1 1 2 2 1 0 1]

python kmeans.py --iterations 3 --clusters 4 --examples 90
Přiřazené skupiny:
[2 1 1 0 1 0 3 1 0 3 1 3 1 0 1 2 3 1 2 1 1 1 1 0 0 1 1 3 2 1 1 1 2 2 1 1 1
1 0 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 2 0 0 2 0 0 0 3 1 0 1 1 1 1 0 3 1 3 1
1 1 1 3 2 0 1 3 0 0 3 2 3 0 0 0]

PCA
Další problém, na který můžete narazit, je vizualizace dat. U datasetu, kde máme dvě/tři featury, se dají data ještě vcelku jednoduše vizualizovat, ale co když má dataset více featur? Typický dataset bude mít desítky až tisíce featur a nevím jak vy, ale představit si už 4D prostor je pro mne vcelku obtížné a více dimenzí by bylo ještě obtížnější. Naštěstí existuje užitečný algoritmus, který udělá kompresi dat do méně dimenzí. Tento algoritmus se nazývá PCA (Principal Component Analysis) neboli Analýza hlavních komponent. Zjednodušeně si můžeme představit, že PCA nám najde osy (featury), které když zachováme a ostatní odstraníme, tak ztratíme nejméně informací. Ve skutečnosti hledáme nějaké zobrazení dat z n dimenzí do m dimenzí, kde m < n a ztráta informace je minimální. Samotné vypočítání PCA je jen aplikování lineární algebry pomocí tzv. SVD dekompozice.
Aplikací PCA je kromě vizualizace dat i např. komprese dat nebo feature extraction (zjištění/vygenerování m nejdůležitějších featur pro daný problém).
Neuronové sítě
V seriálu jsme se zatím nedotkli neuronových sítí. My si zde popíšeme jeden typ neuronových sítí, tzv. dopředné neuronové sítě (feedforward neural networks). Tyto sítě vypadají tak, že mají několik vrstev neuronů. Každý neuron v jedné vrstvě přijímá jako vstup výstupy od všech neuronů z předešlé vrstvy. Každý neuron je jeden lineární model (lineární regrese) s nelineární aktivací. Typicky uvažujeme první vrstvu jako vstupní vrstvu a je trochu falešná, protože výstup z této vrstvy představují vstupní data.
Když si vzpomeneme na 3. díl seriálu, tak prakticky jednu vrstvu neuronové sítě jsme již napsali, když jsme implementovali klasifikaci do více tříd pomocí softmax aktivace.
Dále připomeneme, že nelineární aktivační funkce je důležitá, protože bez ní by se celá síť dala zjednodušit na jen jednu vrstvu, protože složením lineárních funkcí dostaneme opět lineární funkci. Což jinými slovy znamená, že bychom si více vrstvami vůbec nepomohli a stačila by nám jediná vrstva.
Např. když budeme mít dvě funkce, jedna z nich bude ke vstupu přičítat jedničku a druhá bude svůj vstup násobit dvěma, tak tyto dvě funkce dokážeme popsat jednou funkcí, která bude vstup násobit dvěma a přičítat dvojku.
Asi vás nepřekvapí, že učení neuronových sítí se dělá pomocí gradientů (stejně jako u lineární či logistické regrese). Jen namísto jednoho neuronu (u lineární regrese) či jedné vrstvy (u klasifikace do více tříd pomocí softmaxu) máme více vrstev neuronů s nelineárními aktivacemi. Nejběžněji používaná nelineární funkce na skrytých vrstvách neuronových sítí (vrstvách, které nejsou vstupní ani výstupní) je ReLU (Rectified Linear Unit) či jeho varianty. Tato funkce je velice jednoduchá, pro kladné hodnoty se funkce chová jako identita (tedy f(x) = x) a pro nekladné hodnoty je funkce nulová (tedy f(x) = 0). Dříve se běžně používala funkce hyperbolický tangens, dnes již méně často.
Učení neuronových sítí
 Tento odstavec je náročnější a není vyžadována
znalost této sekce v seriálových úkolech.
Pro následující odstavec je doporučené si nejdříve přečíst
předchozí díly seriálu.
Navíc výsledky derivací jsou zde jen uvedené a nezabýváme se
přesným výpočtem. Pokud nějakému výsledku nevěříte, tak
si můžete zkusit derivovat podle jednotlivých parametrů
(ne podle celého vektoru)
a poté výsledek složit do finální matice.
Tento odstavec je náročnější a není vyžadována
znalost této sekce v seriálových úkolech.
Pro následující odstavec je doporučené si nejdříve přečíst
předchozí díly seriálu.
Navíc výsledky derivací jsou zde jen uvedené a nezabýváme se
přesným výpočtem. Pokud nějakému výsledku nevěříte, tak
si můžete zkusit derivovat podle jednotlivých parametrů
(ne podle celého vektoru)
a poté výsledek složit do finální matice.
Jelikož jsme v prvním a třetím díle seriálu již vypočítali skoro všechny potřebné derivace, tak učení neuronových sítí bude prakticky jen skládání těchto výpočtů do řetězového pravidla. Na rozdíl od lineárních modelů, kde bias se přidával k vahám, aby se celý výpočet dal udělat pomocí jednoho maticového násobení, u neuronových sítí se toto již spíše nedělá a máme oddělené váhy od biasů. Pro nás to znamená, že budeme muset derivovat i podle biasů pro natrénování sítě. Naštěstí tyto derivace budou triviální.
Nechť máme neuronovou síť s jednou skrytou vrstvou s ReLU aktivací a výstupní vrstvou se softmax aktivací.
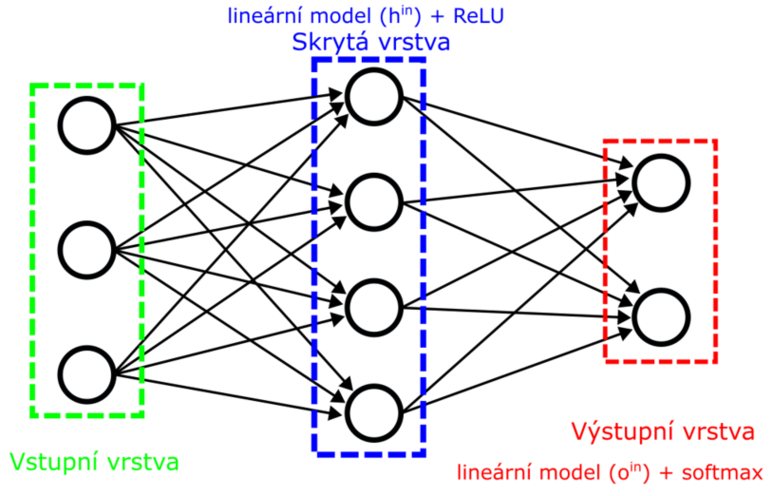
Síť provede následující výpočty těchto funkcí:
| hin(xh) = xh ·wh + bh |
| h(hin) = ReLU(hin) |
| oin(h) = h ·wo + bo |
| o(oin) = softmax(oin) |
| ∂oin |
| ∂bo |
Všimněte si, že model při trénovaní musí trénovat 2 vrstvy vah a biasů. Jednu sadu vah a biasů pro skrytou vrstvu a druhou sadu pro výstupní vrstvu.
Začněme zlehka a ukažme si, jak vypočítáme gradient pro biasy výstupní vrstvy. Jak již je zvykem, tak derivaci budeme počítat pomocí řetězového pravidla.
| ∂L |
| ∂bo |
| ∂L |
| ∂oin |
| ∂oin |
| ∂bo |
| ∂L |
| ∂oin |
| ∂oin |
| ∂bo |
Derivace podle biasů byla vcelku jednoduchá. Derivace podle vah na výstupní vrstvě bude úplně bez práce.
| ∂L |
| ∂wo |
| ∂L |
| ∂oin |
| ∂oin |
| ∂wo |
| ∂L |
| ∂oin |
| ∂oin |
| ∂wo |
Nakonec, zderivujme chybovou funkci podle vah na skryté vrstvě.
| ∂L |
| ∂wh |
| ∂L |
| ∂oin |
| ∂oin |
| ∂h |
| ∂h |
| ∂hin |
| ∂hin |
| ∂wh |
První parciální derivaci známe. Vypočítat druhou není složité, protože funkce oin je lineární model, který derivujeme podle vstupu, což nám dá váhy daného modelu, tedy wo.
Třetí derivace je nejzajímavější, protože zde derivujeme ReLU funkci podle vstupu. Když se podíváme na předpis ReLU funkce, tak vidíme, že pro kladné vstupní hodnoty má derivace hodnotu 1 a pro nekladné vstupní hodnoty je derivace 0. Ekvivalentně můžeme říct, že pokud výstupní hodnoty z ReLU funkce jsou nuly, tak derivace je nula a jinak je derivace jedna.
Poslední derivaci už známe, protože to je další derivace lineárního modelu podle vah a výsledek bude xh.
Derivace pro biasy na skryté vrstvě bude podobná jako derivace pro váhy na skryté vrstvě. Celý výpočet kromě poslední derivace bude stejný a poslední derivace vyjde vektor jedniček.
Není násobení jako násobení
Na začátku je dobré si ujasnit jednu věc. I když v realitě xh může být matice, protože chceme počítat výstup pro více dat najednou, tak funkce pořád derivujeme jen podle jednoho data (podle vektoru). Proč? Technicky, lineární funkce jsou zobrazení z Rn do Rm a tyto funkce nic nevědí o více než jednom datu. To, že jako vstup dáme matici (batch dat) a díky maticovému násobení dostaneme výstupy pro batch dat, je jen výhoda maticového násobení.
U parciálních derivací píšeme, že se tyto výsledky vynásobí, ale nemusí být jasné, jakou operaci máme použít, protože výsledky jednotlivých parciálních derivací jsou matice a vektory. V obecnosti jsou všechny násobení maticová, ale je tu výjimka a to je u ReLU funkce.
Proč tomu tak je? Když bereme ReLU funkci jako zobrazení z Rn do Rn, tak když derivujeme funkci podle vstupů, (tedy derivujeme vektor velikosti n vektorem velikosti n), tak matematická analýza říká, že výsledek je matice n ×n a této matici se říká Jakobián (Jacobian). Ha! Pokud bychom ReLU derivovali úplně podle definic, tak dostaneme matici a zde musíme použít maticové násobení, ale my jsme popsali výsledek derivace ReLU tak, že výsledek je vektor! Jak jsme to mohli udělat? Když bychom udělali výpočet podle definice, tak dostaneme matici, kde na diagonále budou jedničky nebo nuly podle popsaného pravidla pro derivaci ReLU a mimo diagonálu budou nuly. Tento přístup má nevýhodu, že danou matici musíme nějak vytvořit a zbytečně budeme alokovat paměť. Ale existuje tu optimalizace. Víme, že jen diagonála může mít nenulové hodnoty, tedy jen diagonála má vliv na výsledek. Když si rozmyslíte, jak figuruje diagonála v maticovém násobení, tak zjistíte, že stačí si uložit jen diagonálu a násobit dva vektory po složkách. Druhá nevýhoda je, že u tohoto výpočtu se celkem blbě rozmýšlí, jak by měl fungovat pro více dat naráz.
Druhé zdůvodnění je, že funkci ReLU můžeme chápat jako zobrazení z R do R a derivace skaláru podle skaláru je skalár. Navíc u skaláru je jen jedno možné násobení – po složkách.
Úkol 2 – Bonusový úkol: Implementace neuronové sítě [0b]
Pro zájemce, kteří se chtějí utvrdit v tom, že pochopili derivace neuronových sítí, tak jsme připravili bonusový úkol. Naimplementujte výše zmíněnou neuronovou síť, tedy síť s jednou skrytou vrstvou s ReLU aktivací a výstupní vrstvou se softmaxem. Jako obvykle jsme pro vás připravili šablonu, která načítá různé parametry jako počet neuronů na skryté vrstvě, vytvoří náhodně inicializované váhy a biasy.
Ukázka použití (výstup byste měli mít stejný).
python mlp.py
Epoch 1: train acc 91.1%, test acc 89.2%
Epoch 2: train acc 95.9%, test acc 93.5%
Epoch 3: train acc 96.5%, test acc 95.2%
Epoch 4: train acc 96.1%, test acc 94.5%
Epoch 5: train acc 96.3%, test acc 93.5%
Epoch 6: train acc 98.3%, test acc 96.2%
Epoch 7: train acc 98.4%, test acc 96.4%
Epoch 8: train acc 98.3%, test acc 95.7%
Epoch 9: train acc 99.1%, test acc 97.4%
Epoch 10: train acc 98.8%, test acc 97.4%
Využití neuronových sítí
V dnešní době jsou neuronky použity prakticky všude. Jedna z nesporných výhod je, že si dokáží generovat nové featury dat. Například nemusíme ručně vytvářet polynomiální featury do nějakého stupně. Pokud neuronka zjistí, že je užitečné si tyto featury vytvořit, tak si je vytvoří.
Pěkný náhled je, že skryté vrstvy neuronek vytváří nějaké featury a výstupní vrstva využije tyto featury k vytvoření predikce.
Samozřejmě, neuronka není všespásná a pokud je nějaká featura kategorická, tak tuto danou featuru musíme nejdřív one hot encodovat (či nějak jinak zakódovat), protože neuronka vidí číslo a neví, že to číslo znamená např. sobotu. Musíme si dát pozor, že se neuronkám úplně nelíbí, když vstupní featury mají velký rozptyl. Vždy doporučuji data normalizovat.
Doporučuji nedělat neuronky příliš hluboké, protože tyto nejjednodušší neuronky se přestanou po nějaké hloubce učit. Tím, proč tomu tak je, se už zabývat nebudeme, ale varuji vás, abyste nebyli překvapení.
Jedna z nevýhod neuronových sítí je, že potřebují veliké datasety na trénovaní. Pokud máte jen pár stovek dat, tak neuronka nebude nejspíš dobře fungovat a dost pravděpodobně ji převálcují jednodušší modely jako je logistická regrese.
Vytvoření neuronové sítě
V knihovně scikit-learn je možné si vytvořit neuronky
pomocí třídy MLPClassifier či MLPRegressor,
kde můžete nastavit spoustu parametrů, ale pro začátek
je nejzajímavější počet vrstev, počet neuronů v každé vrstvě
a aktivační funkce.
from sklearn.datasets import load_digits
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
mlp = MLPClassifier([100, 100], activation='relu')
data, target = load_digits(return_X_y=True)
mlp.fit(data[:-100], target[:-100])
prediction = mlp.predict(data[-100:])
print(accuracy_score(target[-100:], prediction))
V ukázce vytváříme neuronku o 2 skrytých vrstvách s 100 neurony na každé vrstvě a výstupní vrstva je klasifikační (softmax). Model natrénujeme a vypočítáme přesnost na posledních 100 datech, která model neviděl.
Úkol 3 – Simulace PCA pomocí neuronové sítě [4b]
Navrhněte neuronovou síť, která bude simulovat PCA. Technicky jsme nezmiňovali, jak PCA algoritmus funguje, ale pro tuto úlohu to není úplně potřeba. Myšlenka PCA je jednoduchá. Hledáme zobrazení z Rn do Rm, kde m < n. Chceme najít zobrazení takové, že když spočítáme výstup a ten zpět inverzním zobrazením převedeme zpět do Rn, tak ztráta informace bude minimální. Můžete se na PCA dívat jako na kompresi dat, kde hledáte „nejlepší“ kompresní (pravděpodobně ztrátovou) funkci. Chcete navrhnout architekturu sítě, která bude generovat z n featur m featur, kde m < n. U řešení uveďte, jak byste síť trénovali. Klidně můžete dodat i kód, ale není to nutné.
Jako ztrátovou funkci uvažujme MSE (mean squared error).
Tip: Naučenou síť můžete upravovat, například vyhazovat vrstvy.
KNN
Poslední model, který si ukážeme je KNN (K-Nearest Neighbors). Tento model bude fungovat dost odlišně oproti předchozím modelům.
KNN má velice rychlé trénování. Trénování modelu spočívá v tom, že si model uloží všechna trénovací data a jejich třídy. Při predikci se pro tázané dato spočítá vzdálenost ke všem datům a vybere se k nejbližších dat. Výsledek pro klasifikace je nejčastější třída z těchto k dat a pro regresi je průměr těchto k dat.
Úkol 4 – KNN [4b]
Naprogramujte algoritmus KNN. Pro lehčí implementaci jsme připravili šablonu, která načítá různé parametry jako je parametr k či použitý dataset.
Ukázky použití (výstupy byste měli mít stejné). Pro každý příklad připojujeme obrázek, který ukazuje příklad chybné klasifikace dané třídy a nalezených k nejbližších dat.
python knn.py --k 2
K-nn přesnost se 2 sousedy: 85.60%

python knn.py --k 4
K-nn přesnost se 4 sousedy: 87.60%

Úkol 5 – Soutěžní úloha [3b]
Jako poslední úkol bude soutěžní úloha. Z technických důvodů je soutěž zadaná jako samostatná open-datová úloha 36-5-S2, kterou najdete níže. Zdrojový kód soutěžního programu ale přidejte do ZIPu s řešením seriálu.
Poznámky po čarou
KNN je velice jednoduchý model, který není moc efektivní, ale dá se zlepšit! Jedním z možných vylepšení je, že si nemusíme pamatovat všechna trénovací data, ale vybrat si jen ta data, která jsou důležitá pro predikci. Např. pokud data určité třídy leží v nějakém shluku dat, tak stačí si zapamatovat data, která jsou na okrajích shluku. O ostatních datech implicitně víme, že náleží do tohoto shluku. Tomuto modelu se říká SVM (Support Vector Machine).
Další model, který jen zmíním, je Ada Boost, který se snaží vylepšit přístup random forestu. Místo toho, abychom generovali náhodně další stromy, tak se díváme, která data predikujeme pořád špatně. Těmto datům dáváme vyšší váhu při vytváření nových stromů a je více tlačeno, abychom dokázali tato data predikovat správně. Tedy při vytváření dalších stromů se zaměřujeme na data, která predikujeme špatně.
Tento přístup se dá dále vylepšit pomocí Gradient Boosting Trees.
Závěr
Kam pokračovat dále? Pokud se chcete dozvědět více o neuronových sítích, tak doporučuji knihu Deep Learning, která je volně dostupná.
Pokud si chcete rozšířit znalosti obecně o strojovém učení, tak můžeme doporučit se podívat na knížku Pattern Recognition and Machine Learning (taktéž volně dostupná).
Nebo existuje spoustu článků či videí na Youtube. Minimálně ze zmiňovaných knížek si můžete najít jména algoritmů/modelů, na které se můžete podívat.
Seriál je u konce a doufáme, že jste si ho užili a naučili jste se něco nového. Pokud máte jakékoliv otázky k úlohám či se potýkáte s problémy při řešení úloh, tak se nebojte zeptat pomocí Discordu či emailu. Já se s vámi rozloučím a přeji hodně štěstí.
 36-5-S2 Soutěžní úloha seriálu (3 body)
36-5-S2 Soutěžní úloha seriálu (3 body)
Z technických důvodů je 5. úkol seriálu oddělenou úlohou. Odevzdává se jako open-datová úloha 36-5-S2, ale prosíme přiložte do zazipovaného archivu k seriálu i svá řešení tohoto úkolu. Pokud to neuděláte, můžeme vám dodatečně body odebrat.
V této soutěži je povolené používat libovolný model,
který nabízí knihovna scikit-learn.
Jak soutěž bude probíhat? Od nás dostanete trénovací a testovací data. Dále od nás dostanete šablonu, která si v případě potřeby data stáhne a načte je. U trénovacích dat budete mít k dispozici vstupní featury a výstupní hodnoty, ale u testovacích dat budete mít k dispozici jen vstupní featury. Vaším úkolem je natrénovat model na trénovacích datech a predikovat výstupní hodnoty pro testovací data. Dataset můžete různě transformovat (augmentovat), ale nesmíte si přidávat další externí data do trénovacího datasetu. Všechny výstupy musí být generované vaším programem. Toto pravidlo nezakazuje mít v programu pravidla, která výstupy upravují. Tyto predikce poté odevzdáte do odevzdávátka.
Vaším úkolem je vypredikovat, zda email je spam či ne.
Pokud vaše řešení bude splňovat, že na testovacích datech budete mít přesnost (accuracy) minimálně 92,5% (této hodnotě budeme říkat práh), tak dostanete 3 body. Tím ale zábava teprve začíná, protože tímto krokem jste se kvalifikovali do soutěže.
V soutěži budete soutěžit s ostatními řešiteli až o další 3 bonusové body. Abyste věděli, jak si stojíte, tak k této úloze je i dynamická výsledkovka. Na této výsledkovce uvidíte svou accuracy metriku na testovacích datech nebo hodnotu prahu, podle toho, jaká hodnota je horší. Dále na této výsledkovce budete řazeni podle accuracy metriky na testovacích datech. Pokud jste v soutěži, tak sice neuvidíte accuracy metriku, ale pořád budete vědět, kolik lidí je lepší než vy.
Bonusové body se budou udělovat podle následujícího kritéria: Nejlepší první čtvrtina řešitelů řazená podle accuracy metriky, která se kvalifikovala do soutěže, dostane 3 body, druhá čtvrtina dostane 2 body a třetí čtvrtina dostane 1 bod. Bonusové body budou přiděleny po prvním deadlinu pro tento díl seriálu.
Hodně štěstí!